Technische Universitt Berlin Department of Geoinformation Science Geoinformation

Technische Universität Berlin Department of Geoinformation Science Geoinformation Technology: lecture 9 a Triangulated Networks Prof. Dr. Thomas H. Kolbe Institute for Geodesy and Geoinformation Science Technische Universität Berlin Credits: This material is mostly an english translation of the course module no. 2 (‘Geoobjekte und ihre Modellierung‘) of the open e-content platform www. geoinformation. net. WS 2006/07

Triangulated Networks Department of Geoinformation Science 2 T. H. Kolbe – Geoinformation Technology: lecture 9 WS 2006/07

Overview Department of Geoinformation Science triangle networks – “Triangulated Irregular Networks“ (TINs) modelling of the relief by TINs Delaunay TINs: ‘especially good‘ TINs break lines in the relief: Constrained Delaunay TINs triangulated networks and hydrography 3 T. H. Kolbe – Geoinformation Technology: lecture 9 WS 2006/07
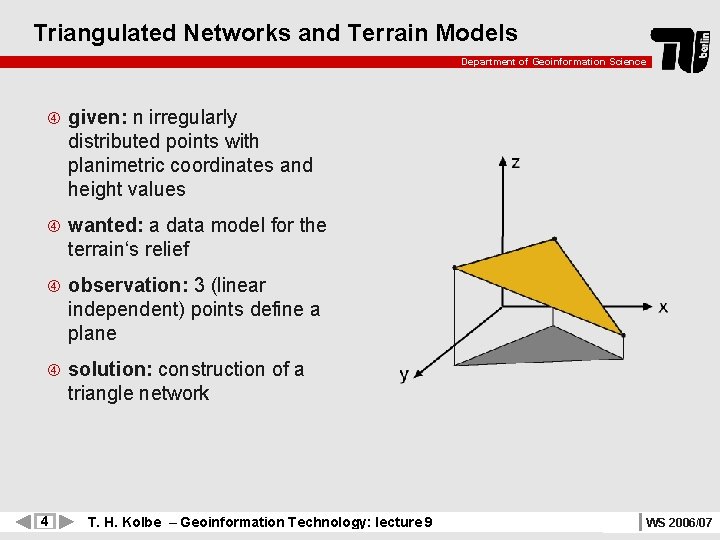
Triangulated Networks and Terrain Models Department of Geoinformation Science given: n irregularly distributed points with planimetric coordinates and height values wanted: a data model for the terrain‘s relief observation: 3 (linear independent) points define a plane solution: construction of a triangle network 4 T. H. Kolbe – Geoinformation Technology: lecture 9 WS 2006/07

Triangulated Networks and Contour Lines Department of Geoinformation Science 5 T. H. Kolbe – Geoinformation Technology: lecture 9 WS 2006/07
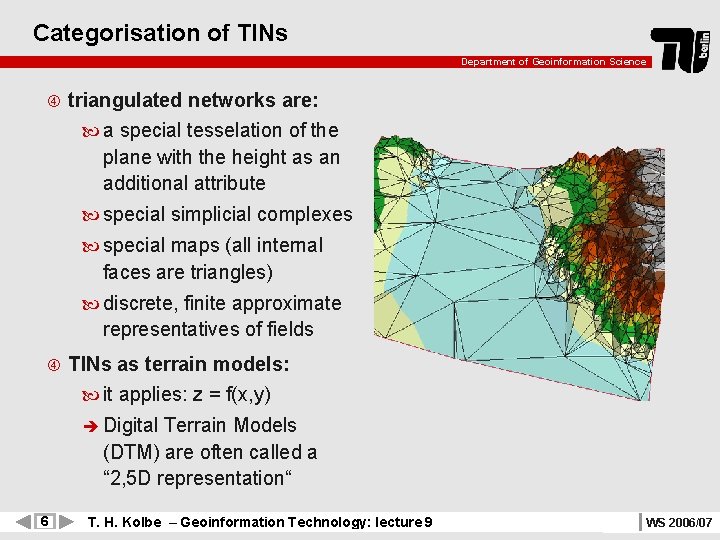
Categorisation of TINs Department of Geoinformation Science triangulated networks are: a special tesselation of the plane with the height as an additional attribute special simplicial complexes special maps (all internal faces are triangles) discrete, finite approximate representatives of fields TINs as terrain models: it applies: z = f(x, y) è Digital Terrain Models (DTM) are often called a “ 2, 5 D representation“ 6 T. H. Kolbe – Geoinformation Technology: lecture 9 WS 2006/07

“Bad“ and “Good“ Triangulated Networks Department of Geoinformation Science usual triangulation may generate sharply peaked triangles Delaunay. Triangulation with minimum (interior) angles 7 T. H. Kolbe – Geoinformation Technology: lecture 9 WS 2006/07
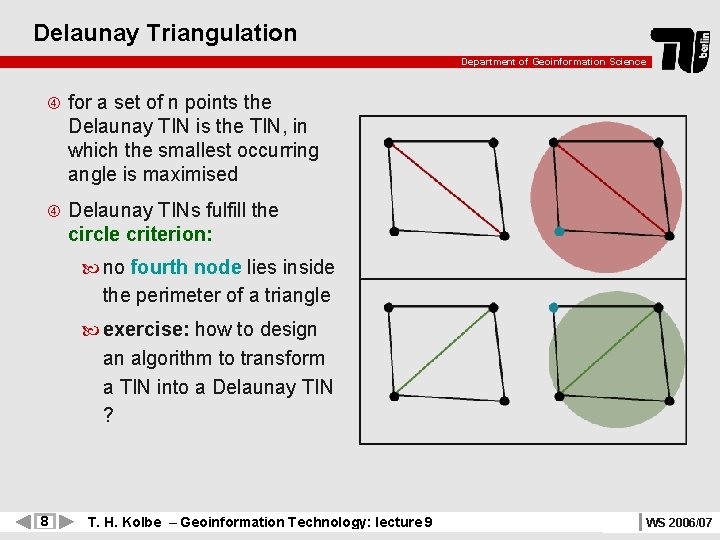
Delaunay Triangulation Department of Geoinformation Science for a set of n points the Delaunay TIN is the TIN, in which the smallest occurring angle is maximised Delaunay TINs fulfill the circle criterion: no fourth node lies inside the perimeter of a triangle exercise: how to design an algorithm to transform a TIN into a Delaunay TIN ? 8 T. H. Kolbe – Geoinformation Technology: lecture 9 WS 2006/07
- Slides: 8