Techniques for developing estimators Methods for finding estimators






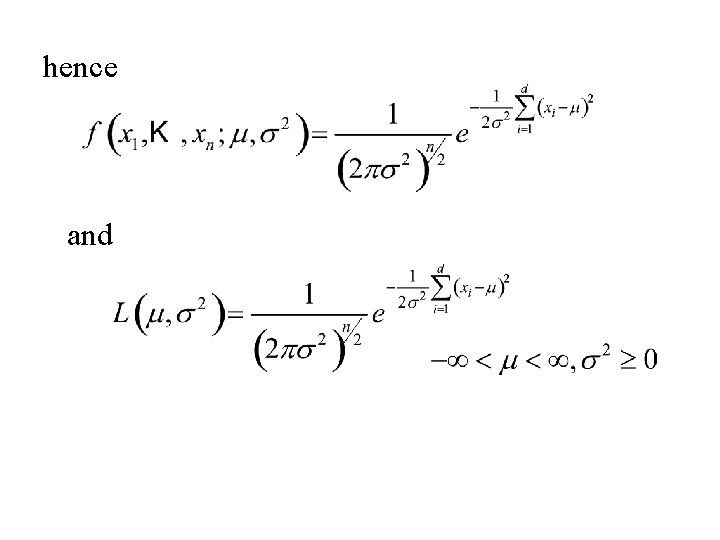

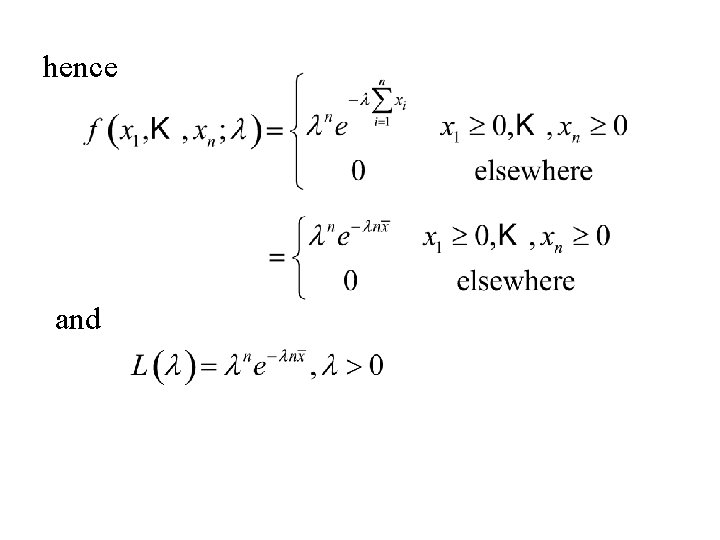



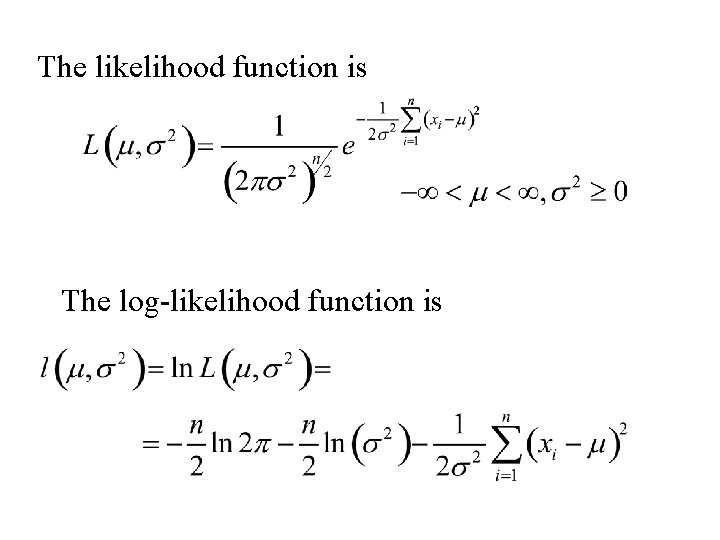
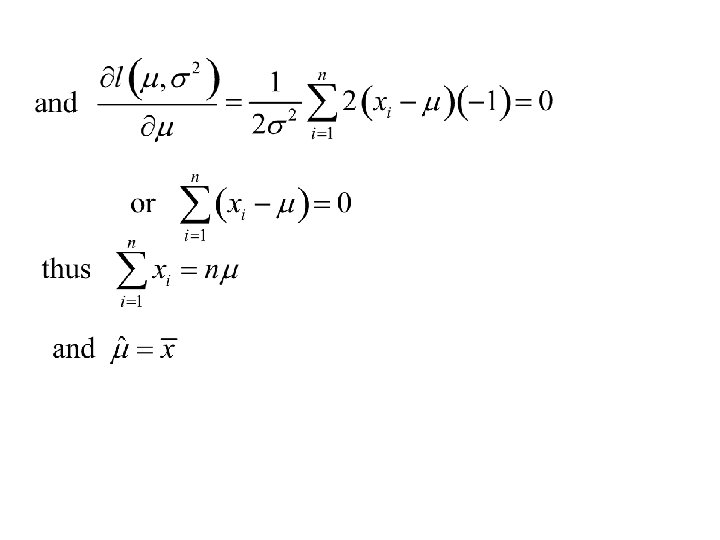
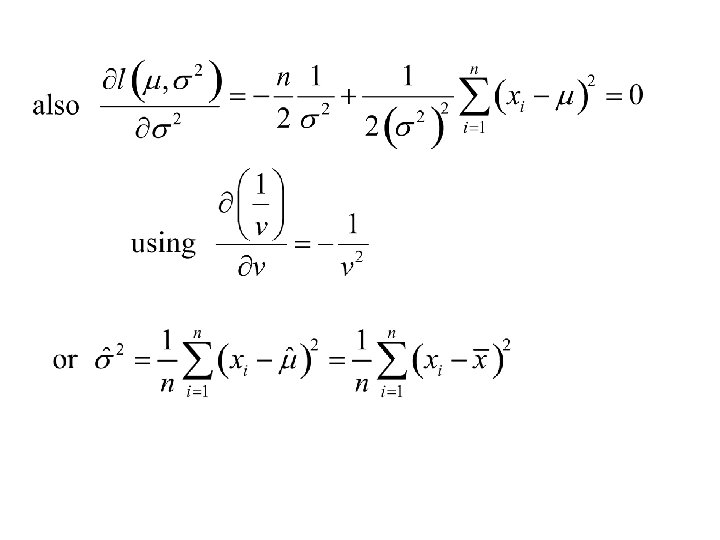



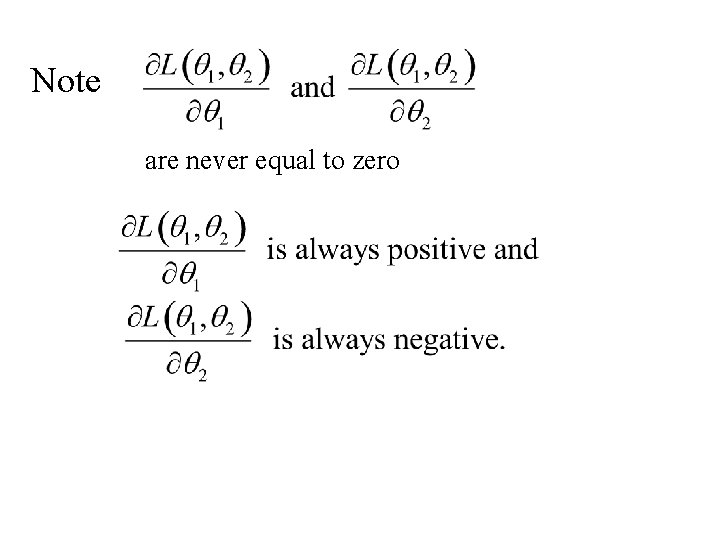



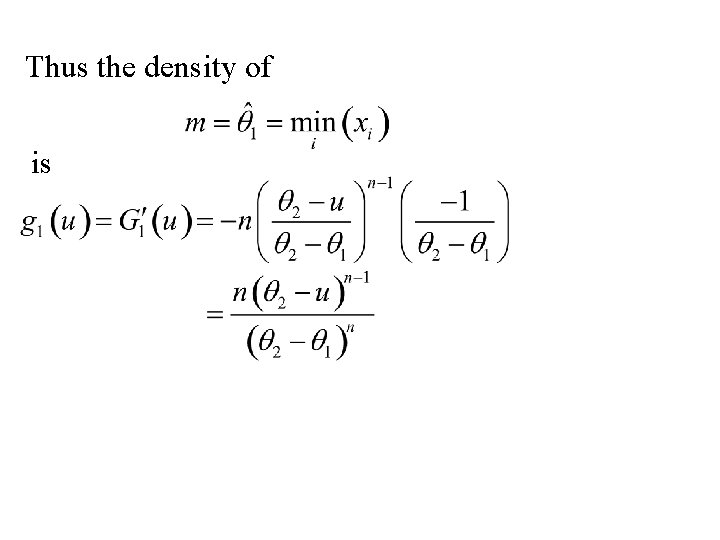
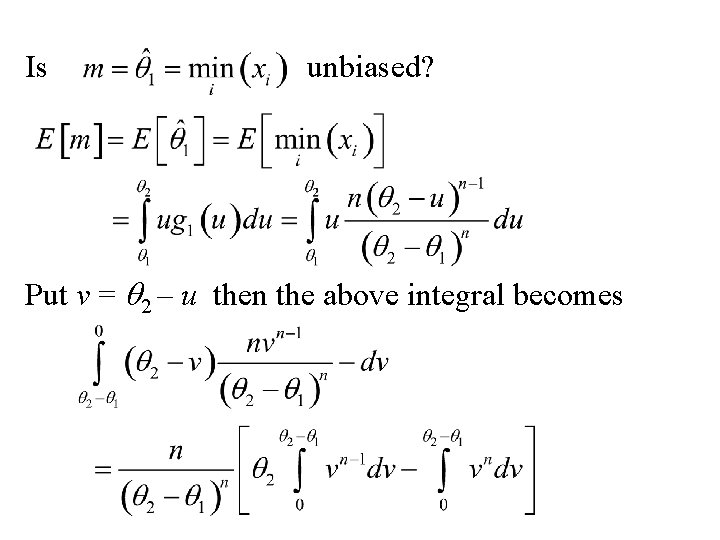
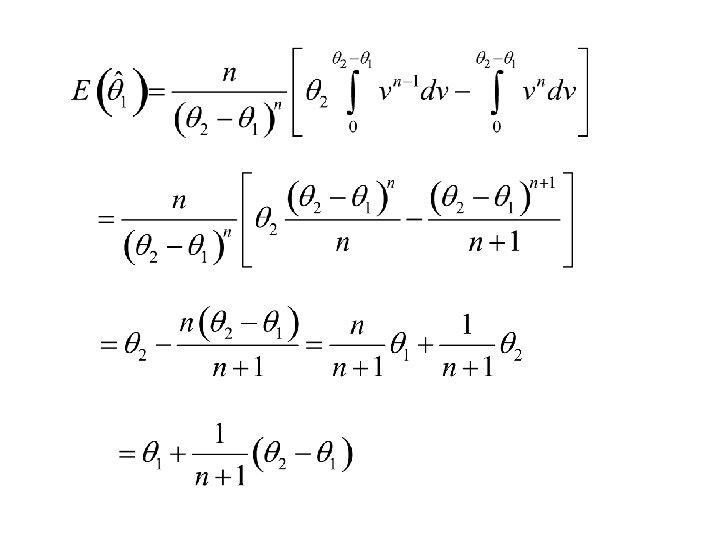
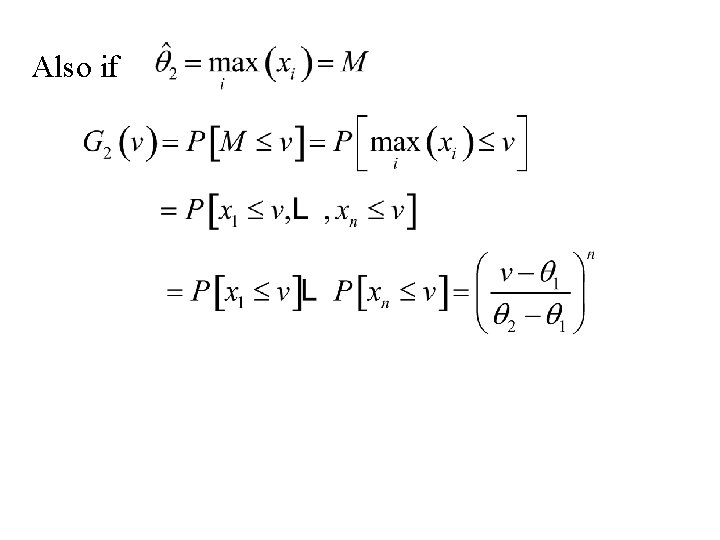
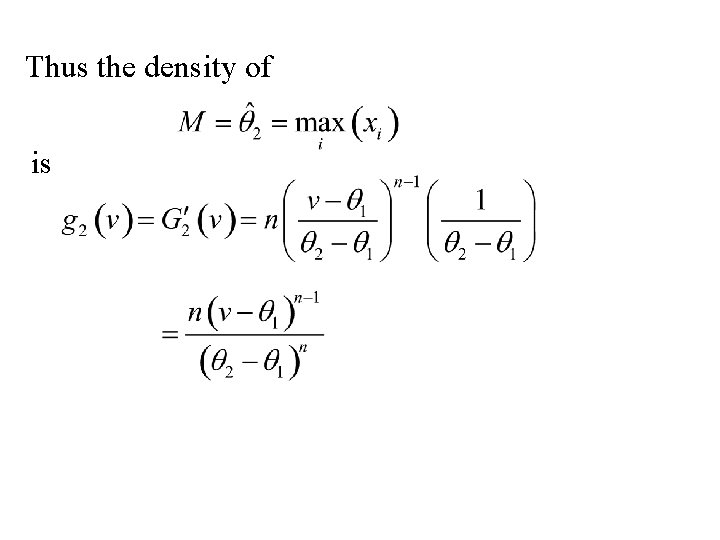
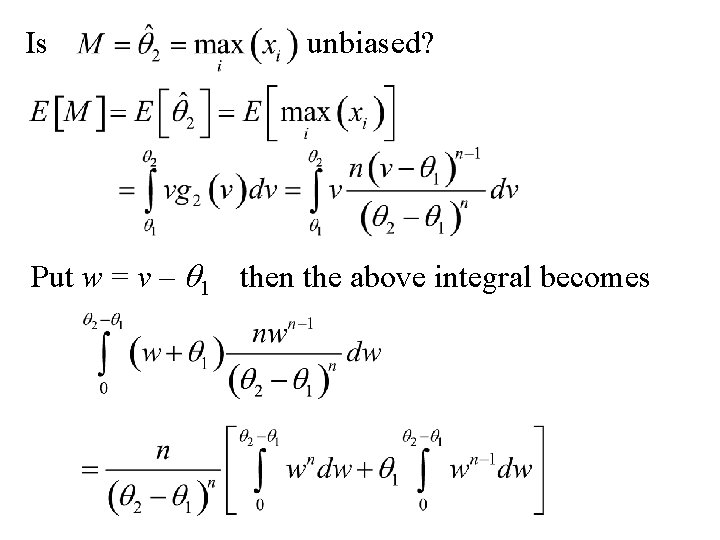
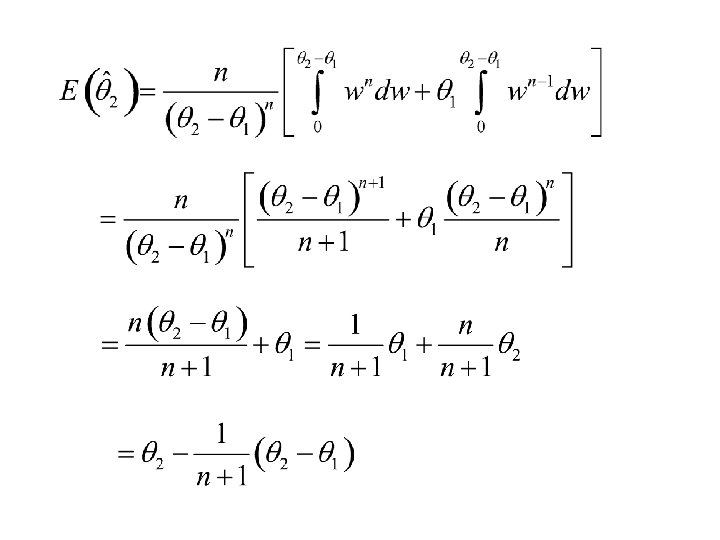
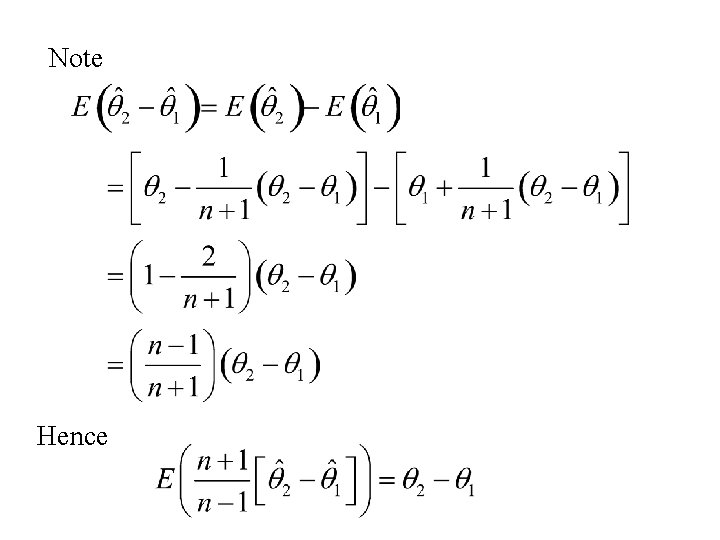
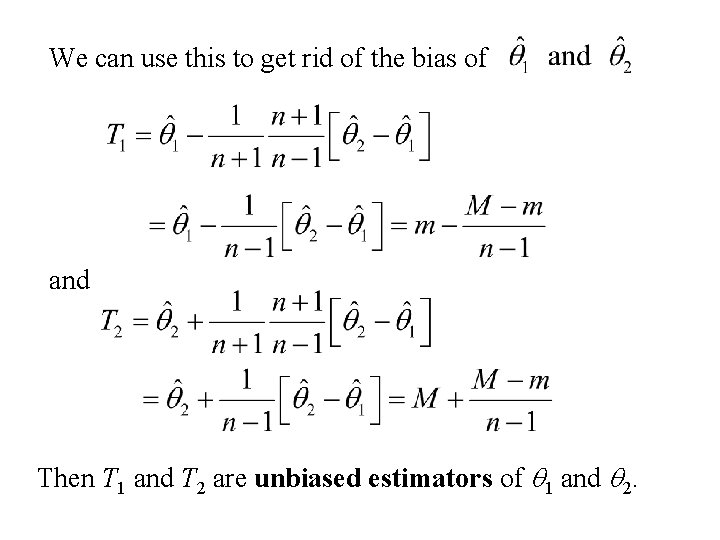







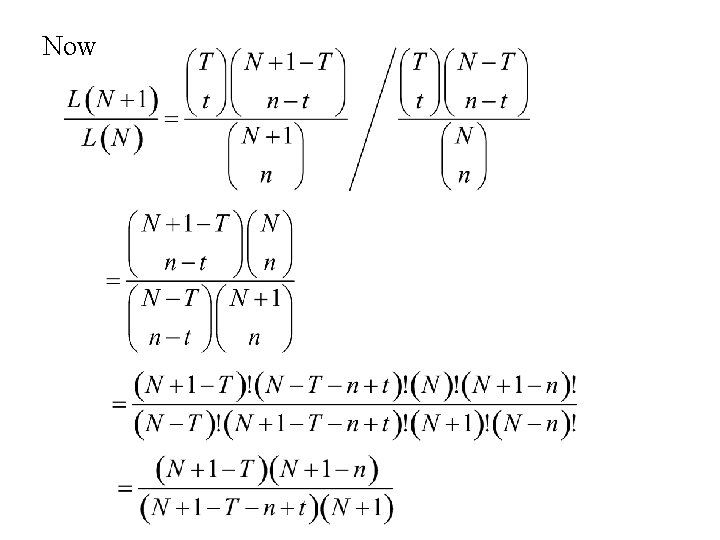
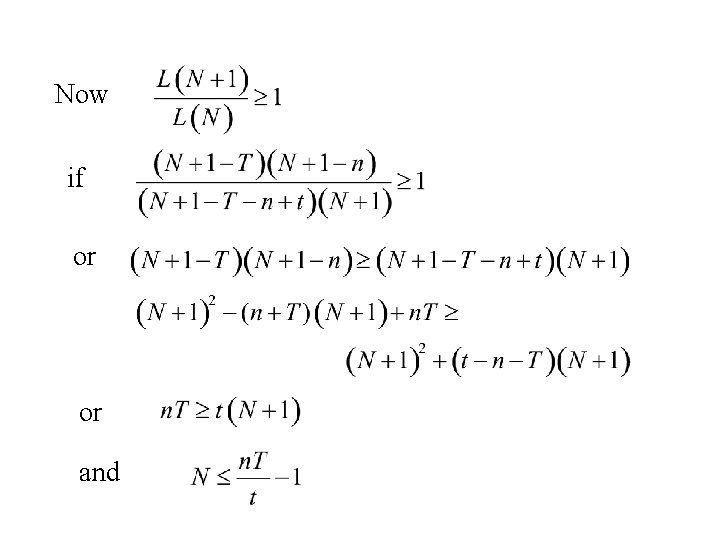

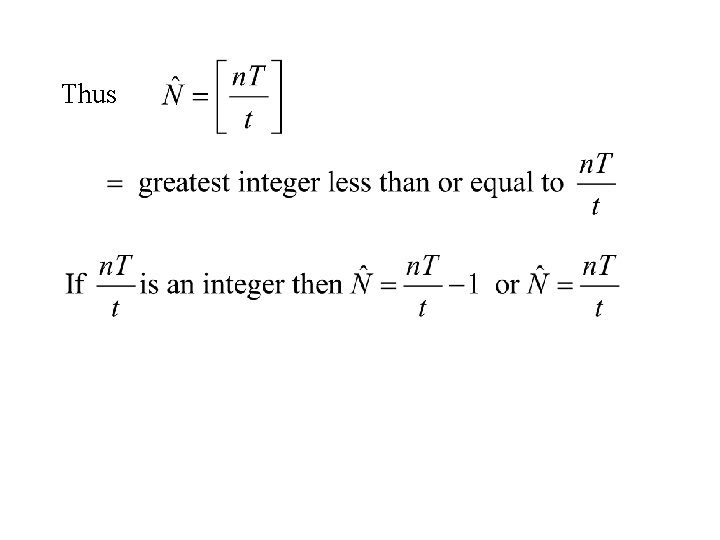
- Slides: 45

Techniques for developing estimators

Methods for finding estimators 1. Method of Moments 2. Maximum Likelihood Estimation

Method of Moments To find the method of moments estimator of q 1, … , qp we set up and solve the equations: The kth sample moment is defined to be:

The Method of Maximum Likelihood Suppose that the data x 1, … , xn has joint density function f(x 1, … , xn ; q 1, … , qp) where q = (q 1, … , qp) are unknown parameters assumed to lie in W (a subset of p-dimensional space). We want to estimate the parametersq 1, … , qp

Definition: Suppose that the data x 1, … , xn has joint density function f(x 1, … , xn ; q 1, … , qp) Then given the data the Likelihood function is defined to be L(q) = L(q 1, … , qp) = f(x 1, … , xn ; q 1, … , qp) Note: the domain of L(q 1, … , qp) is the set W.

Example (of the Likelihood function) Let x 1, … , xn denote a sample from the normal distribution with mean m and variance s 2. The density of xi is: And the joint density of (x 1, x 2, … , xn) is:
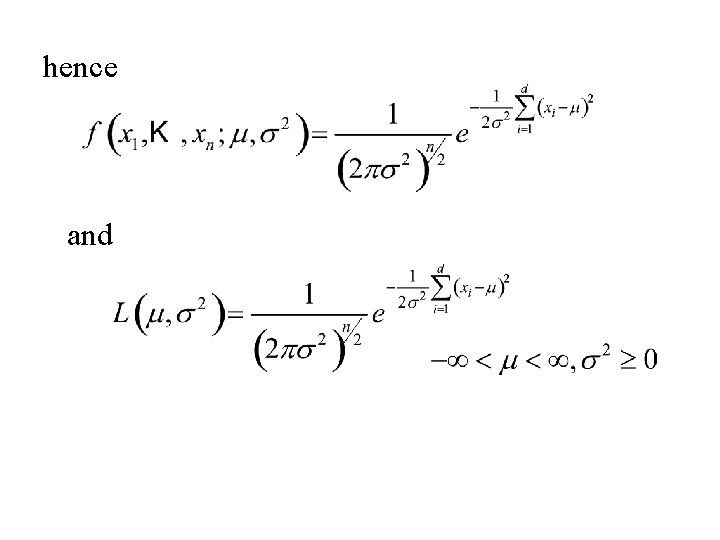
hence and

Example Let x 1, … , xn denote a sample from the exponential distribution with parameter l The density of xi is: And the joint density of (x 1, x 2, … , xn) is:
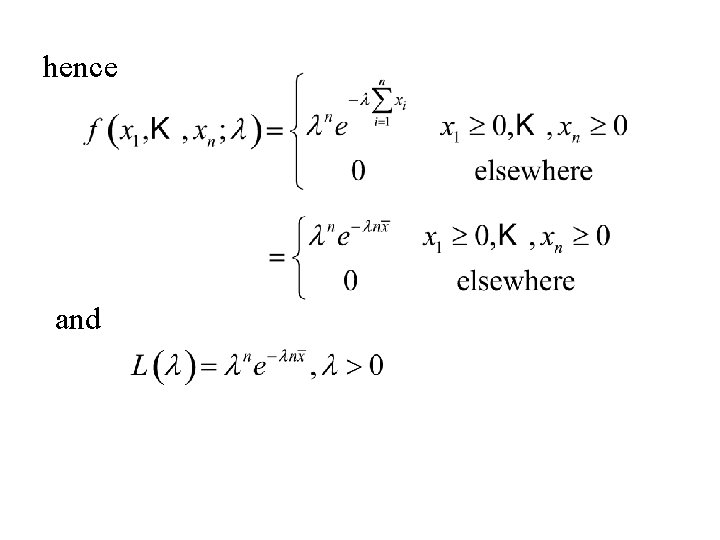
hence and

Definition: Maximum Likelihood Estimators Suppose that the data x 1, … , xn has joint density function f(x 1, … , xn ; q 1, … , qp) Then the Likelihood function is defined to be L(q) = L(q 1, … , qp) = f(x 1, … , xn ; q 1, … , qp) the Maximum Likelihood estimators of the parameters q 1, … , qp are the values that maximize L(q) = L(q 1, … , qp)

the Maximum Likelihood estimators of the parameters q 1, … , qp are the values Such that Note: is equivalent to maximizing the log-likelihood function

Example (of finding a MLE) Let x 1, … , xn denote a sample from the normal distribution with mean m and variance s 2. The density of xi is: And the joint density of (x 1, x 2, … , xn) is:
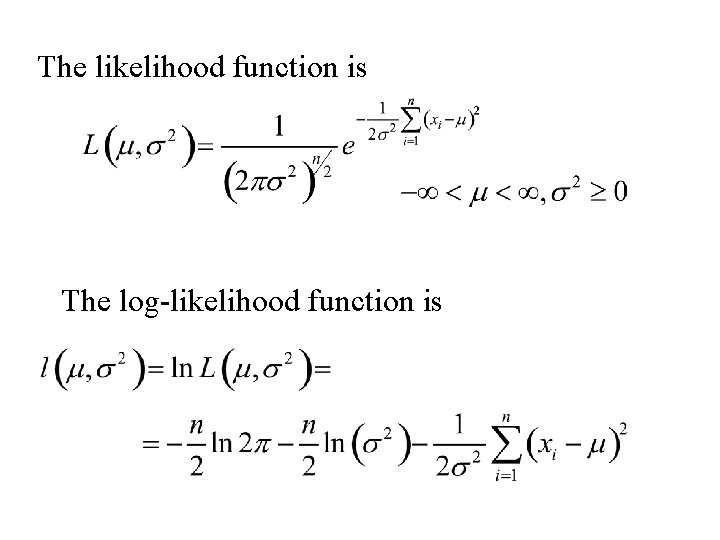
The likelihood function is The log-likelihood function is
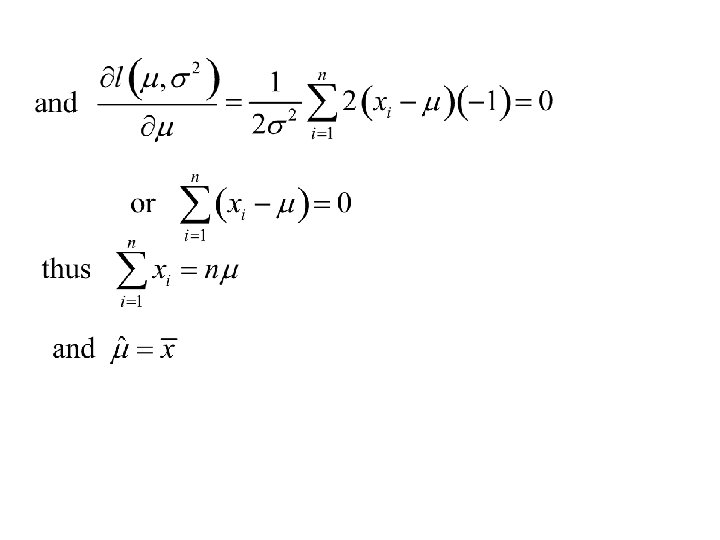
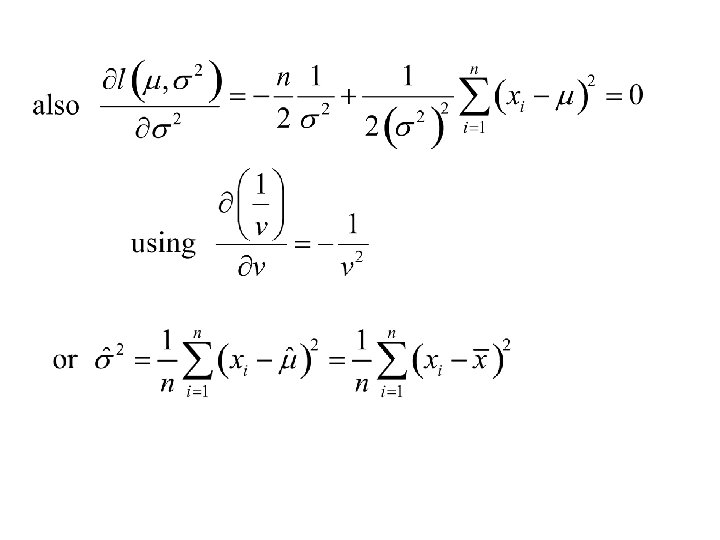

Thus the Maximum. Likelihood estimators of m and s 2 and

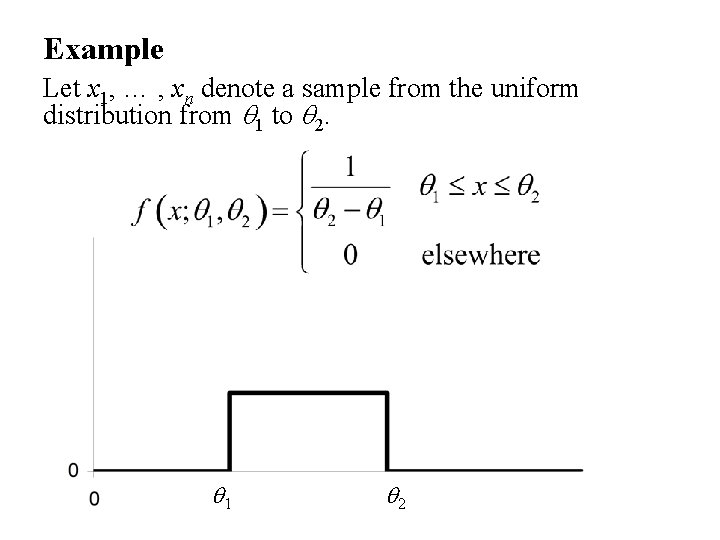
Example Let x 1, … , xn denote a sample from the uniform distribution from q 1 to q 2. q 1 q 2

The joint density of x 1, … , xn is:

To find the maximum likelihood estimates of q 1 and q 2 we determine;
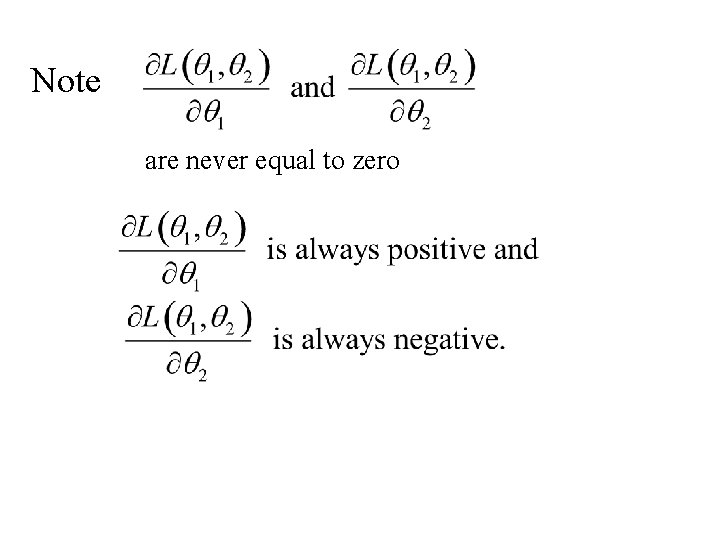
Note are never equal to zero

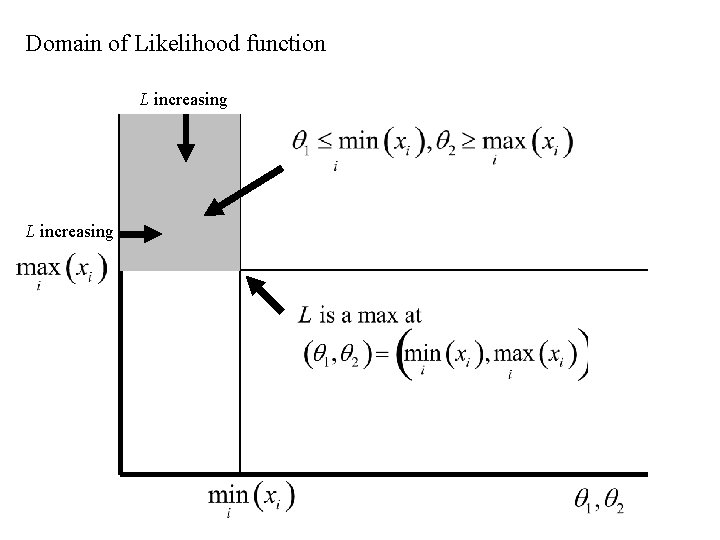
Domain of Likelihood function L increasing

hence the maximum likelihood estimates of q 1 and q 2 are This compares with the Method of moments estimators:

Properties of the maximum Likelihood estimators. What the sampling distribution of Are they unbiased? What is their Mean Square Error?

The sampling distribution: solution We use the distribution function method:
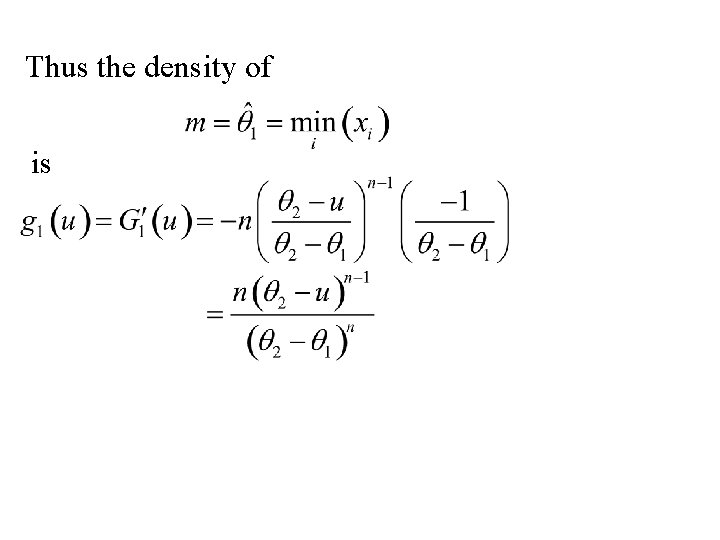
Thus the density of is
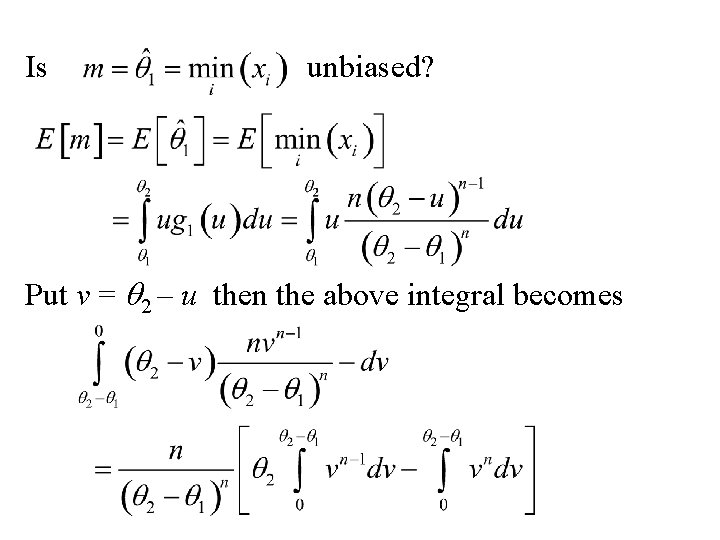
Is unbiased? Put v = q 2 – u then the above integral becomes
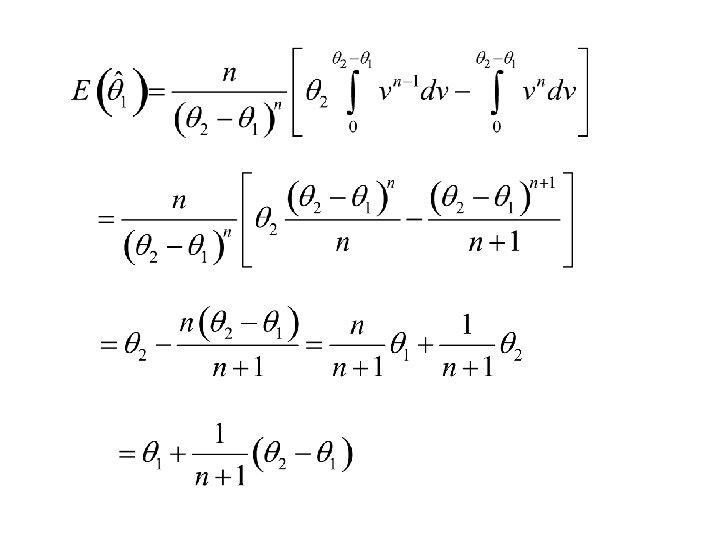
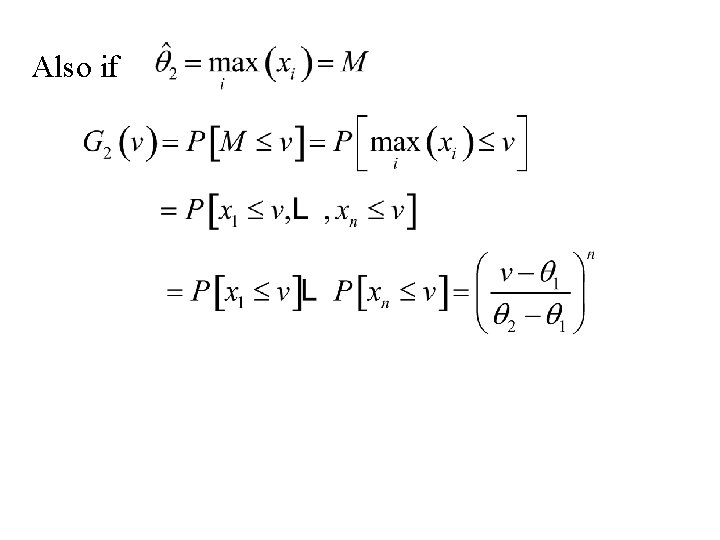
Also if
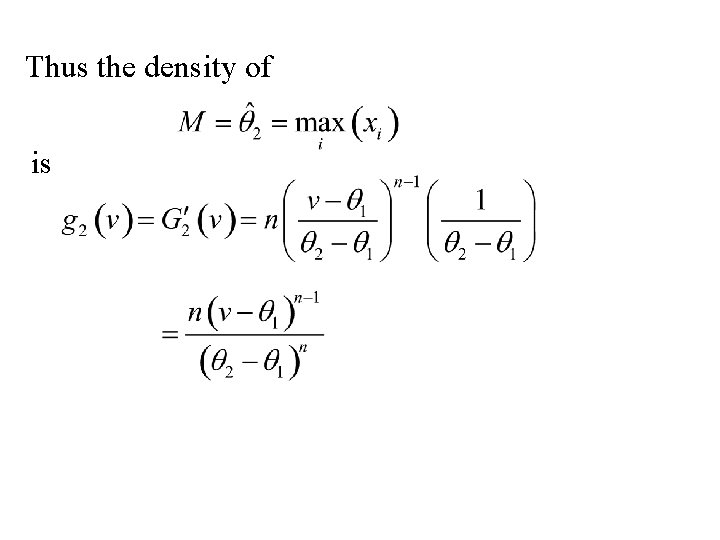
Thus the density of is
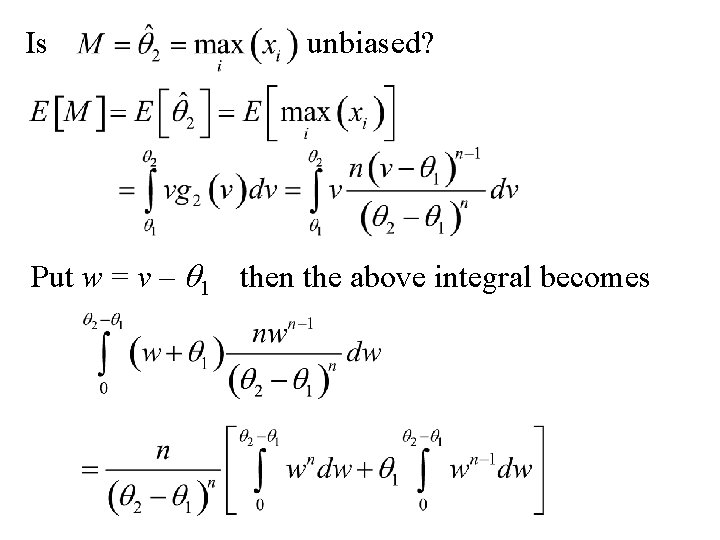
Is unbiased? Put w = v – q 1 then the above integral becomes
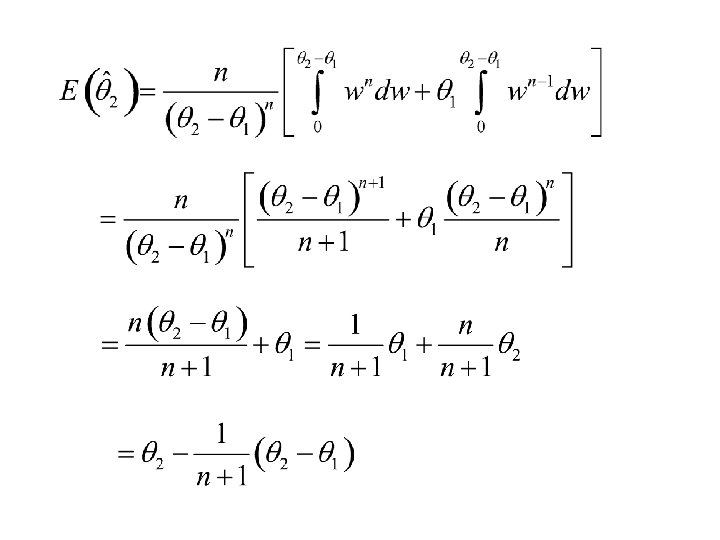
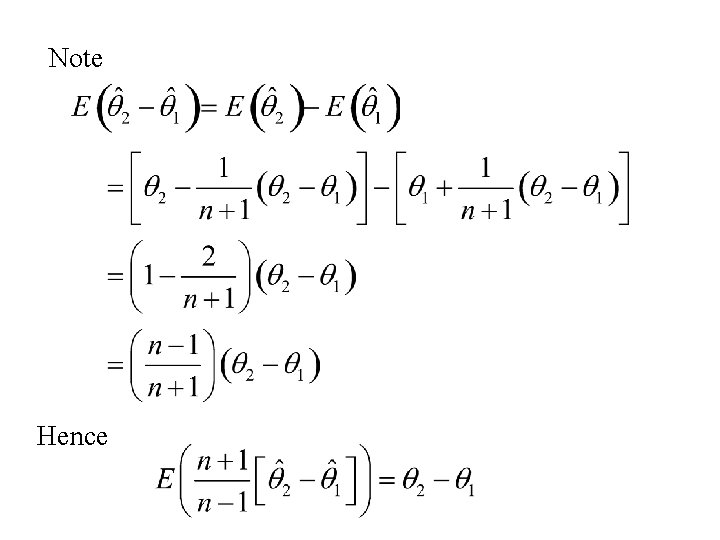
Note Hence
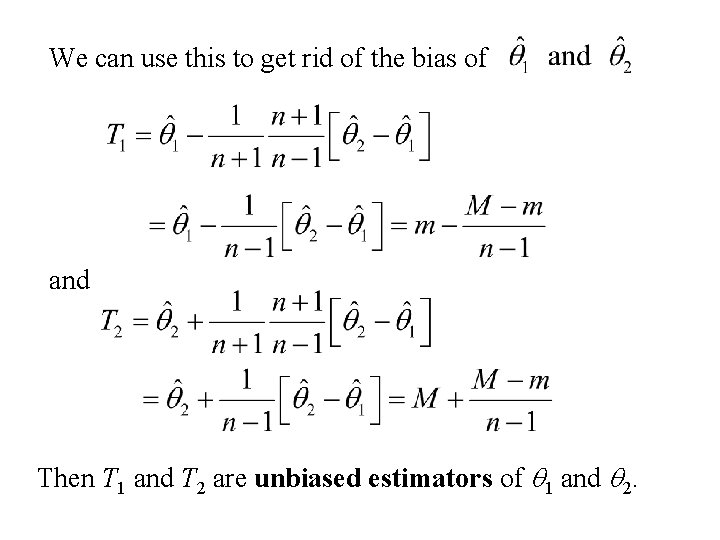
We can use this to get rid of the bias of and Then T 1 and T 2 are unbiased estimators of q 1 and q 2.

Example Let x 1, … , xn denote a sample from the Gamma distribution with parameters a and l.

The joint density of x 1, … , xn is given by:

The log-likelihood function is given by: Differentiating we get:

thus or and where

Hence to compute the maximum likelihood estimates of a and l: 1. We compute 2. Solve the equation for the MLE of a. 3. Then the maximum likelihood estimate of l is

Example: Estimating the size of a wildlife population • Suppose that N (unknown) is the size of a wildlife population. • To estimate N, T animals are caught, tagged and replaced in the population. (T is known) • A second sample of n animals are caught and the number, t, of tagged animals is noted. (n is known and t is the observation that will be used to estimate N).

Note • The observation, t, will have a hypergeometric distribution

To determine when is maximized compute and determine when the ratio is greater than 1 and less than 1.
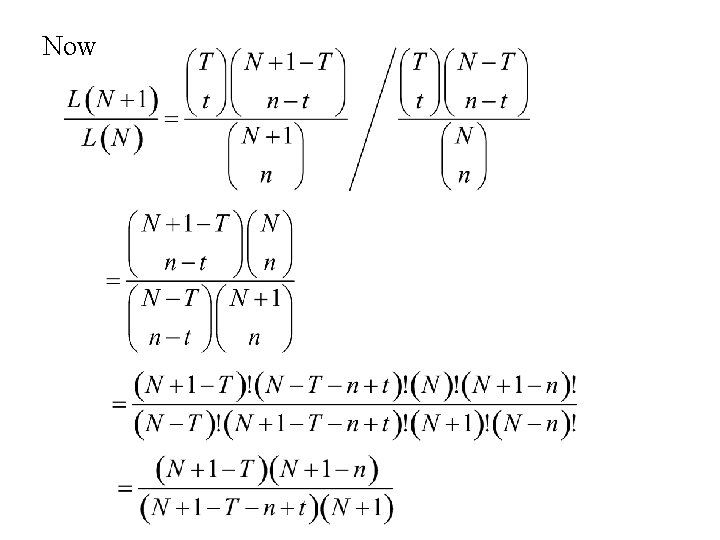
Now
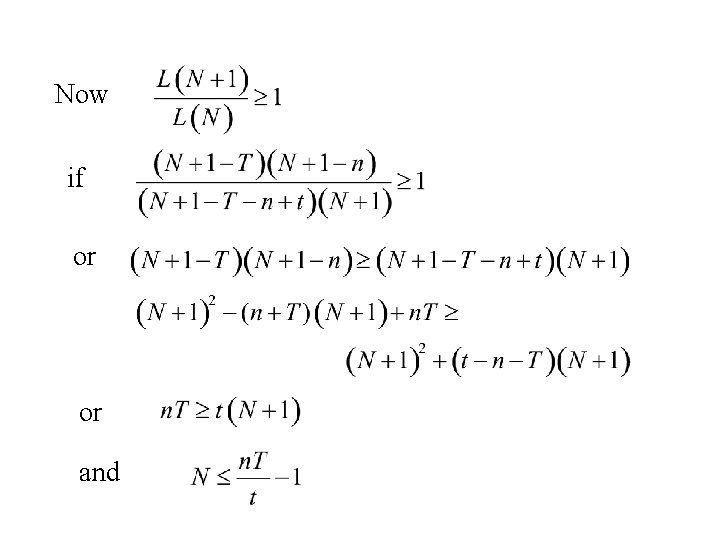
Now if or or and

hence if and if also if
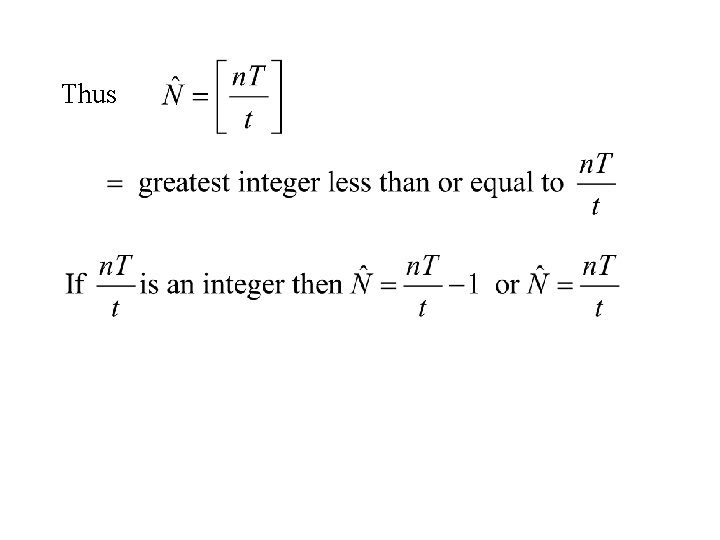
Thus