Teachings For Exercise 10 B Trig Identities and

Teachings For Exercise 10 B

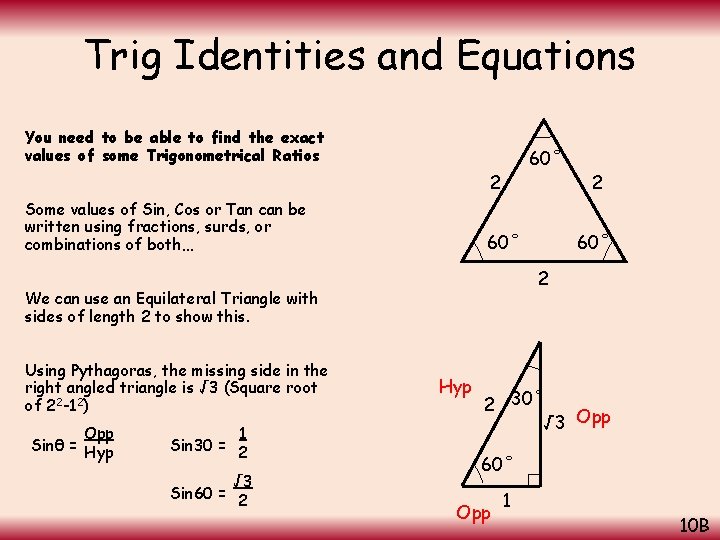
Trig Identities and Equations You need to be able to find the exact values of some Trigonometrical Ratios 60˚ 2 Some values of Sin, Cos or Tan can be written using fractions, surds, or combinations of both… 60˚ Opp Sinθ = Hyp 1 Sin 30 = 2 √ 3 Sin 60 = 2 60˚ 2 We can use an Equilateral Triangle with sides of length 2 to show this. Using Pythagoras, the missing side in the right angled triangle is √ 3 (Square root of 22 -12) 2 Hyp 2 30˚ √ 3 Opp 60˚ Opp 1 10 B

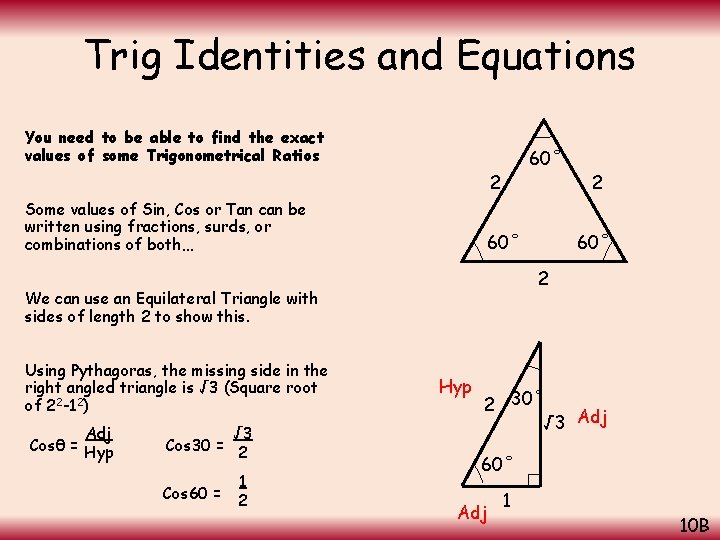
Trig Identities and Equations You need to be able to find the exact values of some Trigonometrical Ratios 60˚ 2 Some values of Sin, Cos or Tan can be written using fractions, surds, or combinations of both… 60˚ Adj Cosθ = Hyp √ 3 Cos 30 = 2 Cos 60 = 1 2 60˚ 2 We can use an Equilateral Triangle with sides of length 2 to show this. Using Pythagoras, the missing side in the right angled triangle is √ 3 (Square root of 22 -12) 2 Hyp 2 30˚ √ 3 Adj 60˚ Adj 1 10 B

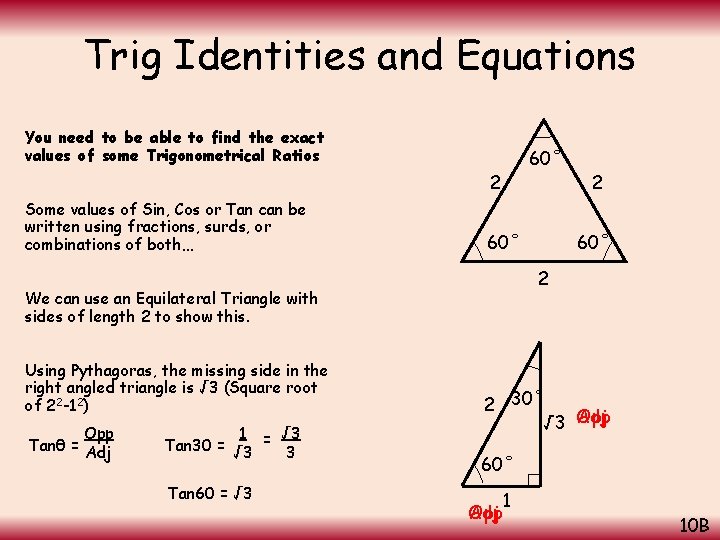
Trig Identities and Equations You need to be able to find the exact values of some Trigonometrical Ratios 60˚ 2 Some values of Sin, Cos or Tan can be written using fractions, surds, or combinations of both… 60˚ Opp Tanθ = Adj 1 √ 3 Tan 30 = √ 3 = 3 Tan 60 = √ 3 60˚ 2 We can use an Equilateral Triangle with sides of length 2 to show this. Using Pythagoras, the missing side in the right angled triangle is √ 3 (Square root of 22 -12) 2 2 30˚ Adj √ 3 Opp 60˚ Opp Adj 1 10 B

Trig Identities and Equations You need to be able to find the exact values of some Trigonometrical Ratios Some values of Sin, Cos or Tan can be written using fractions, surds, or combinations of both… Hyp Opp We can also do a similar demonstration with a right-angled Isosceles triangle, with the equal sides being of length 1 unit. 1 √ 2 45˚ 1 Using Pythagoras’ Theorem, the hypotenuse will be of length √ 2 (Square root of 12 + 12) Opp Sinθ = Hyp 1 Sin 45 = √ 2 2 10 B

Trig Identities and Equations You need to be able to find the exact values of some Trigonometrical Ratios Some values of Sin, Cos or Tan can be written using fractions, surds, or combinations of both… We can also do a similar demonstration with a right-angled Isosceles triangle, with the equal sides being of length 1 unit. Hyp 1 √ 2 45˚ 1 Adj Using Pythagoras’ Theorem, the hypotenuse will be of length √ 2 (Square root of 12 + 12) Adj Cosθ = Hyp 1 Cos 45 = √ 2 2 10 B

Trig Identities and Equations You need to be able to find the exact values of some Trigonometrical Ratios Some values of Sin, Cos or Tan can be written using fractions, surds, or combinations of both… We can also do a similar demonstration with a right-angled Isosceles triangle, with the equal sides being of length 1 unit. Opp 1 √ 2 45˚ 1 Adj Using Pythagoras’ Theorem, the hypotenuse will be of length √ 2 (Square root of 12 + 12) Opp Tanθ = Adj 1 Tan 45 = 1 10 B

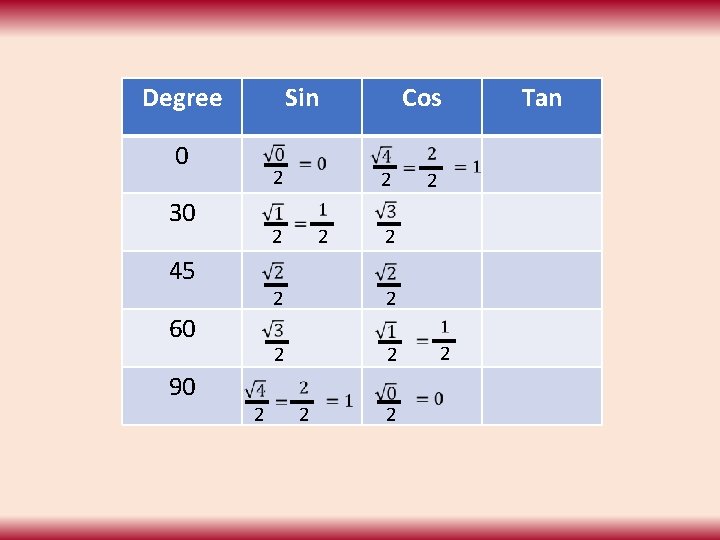
Degree Sin 0 2 30 60 90 2 2 2 45 2 Cos 2 2 2 2 2 Tan