Teaching Practices for Formulating Mathematical Models Kerri Spooner

Teaching Practices for Formulating Mathematical Models Kerri Spooner kspooner@aut. ac. nz Auckland University of Technology May 2016 Kerri Spooner AUT 2015 1

Outline � Rationale and significance � Theoretical background � Student difficulties with modelling � Potential reasons for difficulties � Teacher/Lecturer Implications � Potential research area � Proposed research design

Mathematical Modelling? Mathematical modelling is the process by which we represent a situation in useful mathematical concepts and terms (Dym, 2004; Wake, 1997)

Rationale Why Modelling? � Students difficulties with the formulation stage of the mathematical modelling process (Soon, Tirtasanjaya Lioe, Mc. Innes 2011; Klymchuk, Zverkova, Gruenwald & Sauerbier 2010). � These difficulties are evident but little research done on understanding difficulties. Why Teaching Practices? � Teacher delivery has an influence in removing or creating student difficulties (Crouch & Haines 2004; Blum &Lieb 2007; Stillman, Brown & Galbraith 2010; Blum 2011; Soon et al 2011). � � Research into teaching at university level not well developed (Jokawariski 2016) Research focused on lecturer’s actions and goals and their relation to student learning is lacking (Jokawariski 2016) It is thought that “the creation of the mathematical model” is “perhaps the most difficult stage of modelling” (Soon et al, 2011, pp 1028). Kerri Spooner AUT 2015 5

Significance Modelling Techniques for lecturers on ‘how’ to teach students to model Improved student preparation for workforce Valuable educational experience for both educators and students � Community Analysis of current teaching practices, student difficulties and reason for difficulties Guidelines for effective teaching practices for modelling Improved curriculum design � Personally Contribute to the developing theory of teaching and learning mathematical modelling. Teachers and lecturers to reconsider their pedagogy and beliefs to more effectively teach students. �

Research area - the teaching and learning of mathematical modelling. Research question - how to enhance student’s skills in mathematical modelling? Research focus - teaching practices formulation mathematical models. In particular, lecturer’s actions and goals and their relation to student learning Target group – tertiary lecturers and students Kerri Spooner AUT 2015 7

The intended outcomes – � Find and identify teaching approaches that help students develop their own successful schemas formulating models. � For this work to contribute to the developing theory of teaching and learning mathematical modelling.

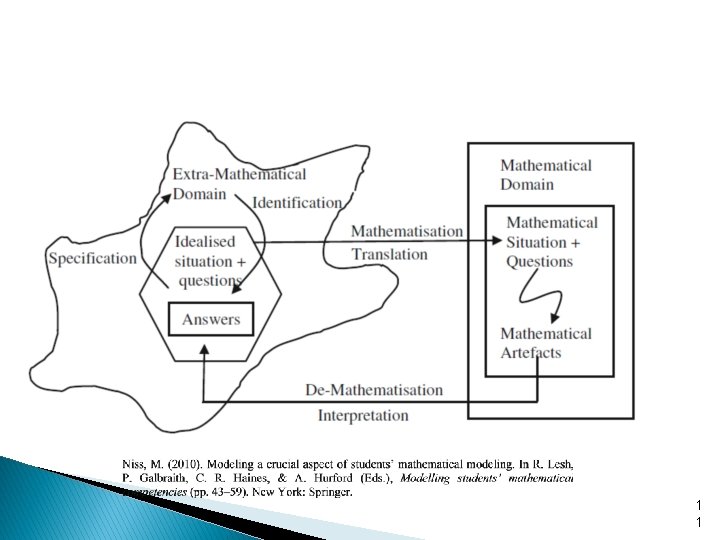
Theoretical Background (based on work with Centre for Maths in Industry, Massey University 2011 and Dym, 2004; Svobodny, 1998; Treilibs et al, 1980) Kerri Spooner AUT 2015 9

Diagrams of MM Process 1 0

1 1

Theoretical frameworks to identify student challenges & opportunities Maab (2006) Blomhoj and Jensen (2007) Galbraith and Stillman (2006) and Stillman et al (2010) Schnaap et al (2011)

Student Challenges �Lack of strategies (Blum &Lieb 2007, Blum 2011, Soon et al 2011, Stillman 2004) - Organisational difficulties (Stillman 2004) Do not consciously use or easily adopt strategies formulating a model (Blum 2011, Blum &Lieb 2007, Soon et al 2011)

�Challenges situation with the context of the (Blum & Lieb 2007, Kadijevich 2008, Klymchuk at al 2010, Stillman 2004). - Ignore context (Stillman 2004). Do not understand wording (Klymchuk et al). Inappropriate assumptions when unfamiliar with the context (Kadijevich 2008).

�Translating from real world to mathematics (DISUM Studies Blum 2011, Soon et al 2011, Klymchuk et al 2010, Palm 2007, Crouch & Haines 2004, Stillman 2004, and Clements, Lochhead, & Monk 1981, Kadijevich 2008, Ikeda & Stephens 2001, Klymchuk & Zverkova 2001, Chaachoua and Saglam 2006, Dominquez, Garza and Zavala 2015, Rowland Jovanoski 2004, Rowland, 2006). - Converting between words and mathematics - Linking physical processes, physics and mathematics (Chaachoua and Saglam 2006, Dominquez, Garza and Zavala (Clements, Lochhead & Monk 1981, Klymchuk et al 2010, Soon et al 2011) 2015, Rowland Jovanoski 2004, Rowland, 2006).

Specific Formulation Difficulties Assigning units to formulae Stillman, Soon Identifying useful equations and formulae Soon, Klymchuk, Stillman Identifying variables Soon Not knowing concept of unknown and known variables Soon Difficulties classifying variables as implicit, independent or dependent Soon, Kadijevich Difficulty recalling relevant formula and procedures Stillman, Klymchuk Difficulties using formula Klymchuk Unable to make assumptions Blum Unable to form equations relating important variables Soon, Klymchuk, Clements, Spooner Know potential relationships but unable to form equation Soon, Spooner Difficulty identifying essential aspects of situation Soon, Blum & Lieb

�Metacognitive - modelling strategies Lack of reflection (Maul & Berry 2002, Soon et al 2011, Stillman et al 2010) Incorrect or incomplete knowledge (Stillman et al 2010) Lack of critical thinking and flexibility in thinking (Stillman et al 2010)

Potential reasons for difficulties One solid reason: students’ lack of systematic approaches et al 2011, Stillman 2004). Little research done, Anecdotal and holistic in nature � Complexity of the process of modelling (Soon

�Lack of previous experience with modelling Culture of solving routine problems with routine solutions (Boaler 2001, Rowland Jovanoski 2004, Rowland 2006, Soon et al 2011). - 1 st year University students with a lack of exposure to non-typical problems experienced difficulties with modelling (Rowland Jovanoski 2004, Rowland 2006, Haines, Crouch & Fitzharris 2003, Haines & Crouch 2001, Klymchuk & Zverkova 2001, Soon at al 2011)

�Teacher/lecturer delivery Evidence points towards teacher/lecturer delivery having an influence in removing or creating student difficulties with modelling - Absence of simulation of strategies by teacher, absence of student strategies (Blum & Lieb 2007)

Teacher/Lecturer Implications � Lack of teacher knowledge about 1988 the SINUS project , Germany 180 schools 2007 DISUM studies , Germany 1500 schools difficulties General lack of teacher knowledge of student difficulties there is a general lack of how teachers should best support modelling practices (Blum & Lieb 2007). Lack of strategies - need to train students to explore, develop, adopt and reflect on strategies and guidelines formulating models. Challenges with context -first stage to understand the context of the problem. Translating between real world and mathematics - More emphasis from an earlier age.

� No widely established method for teaching mathematical modelling. Strategies discussed in literature: - Discussion cycles (Lege 2005, Spooner 2012) - Reflection on strategies (Soon et al 2011, Stillman et al 2010) - Strategic teacher interventions (Blum 2011, Blum & Lieb 2007, Kaiser & Stender 2013) All strategies need further investigation

� Centrality of the educator in mathematical modelling manner (Lipowsky 2006, Blum 2011, Niss 2001, Verschaffel et al 2000) Teacher and manner in which mathematics is taught most important variable. This view supported for modelling. The decisive variable for successful learning of modelling is the teacher/lecturer. What are the key teacher competencies for teaching modelling?

Potential research area What do we know � Students find modelling hard � Little research into why � Teacher/lecturer key to learning What don’t we know � Teaching approaches to address specific difficulties � Effect of lecturer’s actions and goals on student learning � Teacher competencies for modelling

Propose to …. � Analysis different lecturing approaches � Impact on students In particular, lecturer’s actions and goals and their relation to student learning

Theoretical Framework Realistic Mathematics Education � Design Research Local instruction theory � Hypothetical Learning Trajectory (HLT) Learning goals, planned instructional activities & conjectured learning process “the collective development of the student body” � Broad mathematical goal Formulating a mathematical model

Methodology Qualitative Participants � Four University Lecturers � 20+ Student participants from lecturer’s class (sample size subject to change) Sampling � Reflective and purposeful

Proposed Methodology Discussion potential lecturer participants Pilot study 1. Lecturer data � videoed interviews � Videoed observation of lectures � Examination of course notes � Field notes HLT forms framework. Kerri Spooner AUT 2015 29

2. Student data � mathematical modelling activity Evidence for HLT collected from students’ learning activities by: � video observations of activity � Field notes � written work � post activity videoed interview with students Kerri Spooner AUT 2015 30

3. Compare student and lecturer data � � Comparison of HLTs, Actual Learning Trajectory (ALT) and observed learning Evidence of conjectured learning processes? Evidence of HLT goals? Has the HLT supported student learning? Kerri Spooner AUT 2015 31

4. Collation of observed effective teaching approaches formulating a mathematical model � Recommendation of successful components of HLT for teaching practices. Kerri Spooner AUT 2015 32

Data analysis � Inductive � Reliability approach � Credibility = Validity Each piece of student work is an article of analysis.

Results Insights into � patterns of learning � means of supporting such learning � Reconstruction of the learning process students followed

Anticipated that …. . � further insight into the origin of student difficulties. � development of guidelines for the effective teaching of mathematical modelling.

Timeline 2016 Finish ethics application. Carry out field work (lecturer consultation on research design, questionnaires, interviews, lecture observations). Pilot study. Modify research design. Attend and present at international and local conferences relevant to the area of research. � 2017/2018 Carry out main study. Organisation and analysis of the data. Publishing journal articles on the initial findings. Attending international and local conferences for my relevant research communities. Writing of the Ph. D thesis. Submission and defence of the Ph. D thesis. Making recommendations for teaching approaches. �

Publications � Spooner, K. (2014). Preliminaries for a first year course on Modelling. � http: //directorymathsed. net/montenegro/ Spooner, K. (2014). Preliminaries for a first year course on Modelling. � Proceedings of The Future of Mathematics Education in a Connected World Conference. (6 pages). Retrieved from Paper presentation at The Future of Mathematics Education in a Connected World Conference. Montenegro. (peer reviewed). Spooner, K. (2015). Authentic Mathematical Modelling Experiences of Upper Secondary School Students: A Case study. Paper presentation at the conference of the International Community of Teachers of Mathematical Modelling and Applications 17 (ICTMA-17). University of � Nottingham, Nottingham. Spooner, K. (2015). Authentic Mathematical Modelling Experiences of Upper Secondary School Students: A Case study. Submitted book chapter to International Community of Teachers of Mathematical Modelling and Applications book series. (in review).

And it begins….

Reference List � � � � � Armstrong, P. K. , & Bajpai, A. C. (1998). Modelling in GCSE Mathematics. Teaching Mathematics and its Applications, 7 (3), 121– 131. Blomhøj, M. , & Jensen, T. H. (2007). What’s all the fuss about competencies? In W. Blum, P. Galbraith, H. Henn, & M. Niss (Eds. ), Applications and modelling in mathematics education (pp. 45– 56). New York, NY: Springer. Blomhøj, M (2009). Different perspectives in research on the teaching and learning of mathematical modelling – categorising the TSG 21 papers. In M. Blomhøj & S. Carreira (Eds. ) Mathematical applications and modelling in the teaching and learning of mathematics. Proceedings from Topic Study Group 21 at the 11 th International Congress on Mathematical Education in Monterrey, Mexico, July 6– 13, 2008 (pp. 1– 17). Roskilde: Roskilde Univeristy. Blum, W. (1995). What is the role of applications and modelling in mathematics curricula and everyday teaching practice? Tendencies and difficulties. In Blum, W. , Huntley, I. , & Sloyer, C. (Eds) Advances and Perspectives in the Teaching of Mathematical Modelling and Application (pp. 8– 9). Yorklyn, Delaware: Water Street Mathematics. Blum, W. , & Kaiser, G. (1997). Comparative empirical studies of mathematical application skills of English and German learners. Unpublished application to German Research Society. Blum, W. , & Leiß, D. (2005). “Filling up” – the problem of independence-preserving teacher interventions in lessons with demanding modelling tasks. In M. Bosch (Ed. ), Proceedings of the 4 th European Congress of Mathematics Education (pp. 1623– 1633). Gerona, Spain: FUNDEMI IQS – Universitat Ramon Llull. http: //ermeweb. free. fr/CERME 4 WG 13. pdf Blum, W. & Leib, D. (2007). How do students and teachers deal with modelling problems. In C. Haines, P. Galbraith, W. Blum & S. Khan (Eds. ), Mathematical Modelling ICTMA 12 Education, Engineering and Economics (pp. 222 -231). England: Horwood Publishing Ltd. Blum, W. (2011). Can Modelling Be Taught and Learnt? In G. Kaiser, W. Blum, R. Ferri & G. Stillman (Eds. ) Trends in Teaching and Learning of Mathematical Modelling. (pp. 15– 30). New York, NY: Springer. Blum, W (2015). Quality Teaching of Mathematical Modelling: What DO We Know, What Can We Do? The Proceedings of the 12 th International Congress on Mathematical Education, 73– 96, doi: 10. 1007/978 -3_9 Boaler, J. (2001). Mathematical modelling and new theories of learning. Teaching Mathematics and its Applications 20 (3), 121– 128. Burkhardt, H. (2006). Modelling in Mathematics Classrooms: reflections on past developments and the future. Zentralblatt fur Didaktik der Mathematik 2006, 38(2), 178– 195. Chacchoua, H. & Saglam, A. (2006) Modelling by differential equations. Teaching Mathematics and its applications, 25 (1), 15– 22. doi: 10. 1093/teamat/hri 024 Clatworthy, N. J. , & Glbraith, P. L. (1991). Mathematical Modelling in Senior School Mathematics: Implementing an Innovation. Teaching Mathematics and its Applications, 10 (1), 6 – 28. Clement, J. , Lochhead, J. , & Monk, G. (1981). Translation difficulties in learning mathematics. The American Mathematical Monthly, 88(4), 286– 290. Crouch, R. ; & Haines, C. (2004). Mathematical modelling: Transitions between the real world and the mathematical model. International Journal of Mathematics Education, Science and Technology, 35(2), 197– 206. doi: 10. 1080/00207390310001638322 De Lange, J. (1996). Using and Applying Mathematics in Education. In A. Bishop, K. Clements, C. Keitel, J. Kilpatrick, & C. Labrode. (Eds) International Handbook of Mathematics Education (pp 49– 98). London: Kluwer Academic Publishers. Dominguez, A. , Garza, J. & Zavala, G. (2015). Models and Modelling in an Integrated Physics and Mathematics Course. In G. Stillman. , G. Kaier. , W. Blum. & J. Brown (Eds. ), Teaching Mathematical Modelling: Connecting to Research and Practice (pp. . 513– 522). Switzerland: Springer. Dym, C. (2004). Principles of Mathematical Modelling. Amsterdam: Elsevier Academic Press. Galbraith, P. , & Stillman, G. (2006). A framework for identifying student blockages during transitions in the modelling process. Zentralblatt für Didaktik der Mathematik, 38 (2), 143– 162.

� � � � � � Gravemeijer, K. P. E. (1994). Developing Realistic Mathematics Education. Culemborg: Technipress. Gravemeijer, K. & van Eerde, D. (2009). Design Research as a Means for Building a Knowlegde Base for Teachers and Teaching in Mathematics Education. The Elementary School Journal, 109(5), 510– 524. Haines, C. , Crouch, R. & Fitzharris, A. (2003). Deconstructing mathematical modelling: Approaches to problem solving. In Q. Ye, W. Blum, S. Houston, & J. Jiang (Eds. ), Modelling and Mathematics Education and Culture (pp. 41– 53). Chichester: Horwood Publishing Ltd. Haines, C. , & Crouch, R. (2001). Recognizing constructs within mathematical modelling, Teaching Mathematical Applications, 20, 129– 138. doi: 10. 1093/teamat/20. 3. 129 Ikeda, T. & Stephens, M. (2001). The effects of students’ discussion in mathematical modelling. In Matos, J. , Houston, S. , Blum, W. & Carreira, S. (Eds). Modelling and Mathematics Education: ICTMA 9 - Applications in Science and Technology (pp. 381– 390). England: Horwood Publishing Ltd. Julie, C. (2002). The Activity System of School- Teaching Mathematics and Mathematical Modelling. For the Learning of Mathematics, 22 (3), 29– 37. Jokariski, B. (2016). Teaching Mathematics for Student Understanding Seminar, Auckland University of Technology. Kadijevich, D. (2009). Simple spreadsheet modelling by first-year business undergraduate students: Difficulties in the transition from real world problem statement to mathematical model. In M. Blomhøj & S. Carreira (Eds. ) Mathematical applications and modelling in the teaching and learning of mathematics. Proceedings from Topic Study Group 21 at the 11 th International Congress on Mathematical Education in Monterrey, Mexico, July 6 – 13, 2008 (pp. 241– 248). Roskilde: Roskilde Univeristy. Kaiser, G. , Blomhoj, M. & Sriraman, B. (2006). Towards a didactical theory for mathematical modelling. Zentralblatt fur Didaktik der Mathematik, 38 (2), 82– 85. Kaiser, G. & Sriraman, B. (2006). A global survey of international perspectives on modelling in mathematics education. Zentralblatt fur Didaktik der Mathematik, 38 (2), 302– 310. Kaiser, G. & Stender, P. (2013) Complex Modelling Problems in Co-operative, Self-Directed Learning Environments. In G. Stillman, G, Kaiser, W, Blum, J, Brown (Eds. ) Teaching Mathematical Modelling: Connecting to Research and Practice, International Perspectives on the Teaching and Learning of Mathematical Modelling (pp. 277– 293). Dordrecht: Springer. Klymchuk, S. , Zverkova, T. , Gruenwald, N. & Sauer bier, G. (2010). University Students’ Difficulties in Solving Application Problems in Calculus: Student Perspectives. Mathematics Education Research Journal, 22 (1), 81– 91. doi: 10. 1007/BF 03217567 Klymchuk, S. & Zverkova, T. (2001). Role of Mathematical Modelling and Applications in University Mathematics Service Courses: An Across Countries Study. In Matos, J. , Houston, S. , Blum, W. & Carreira, S. (Eds). Modelling and Mathematics Education: ICTMA 9 - Applications in Science and Technology (pp. 227– 234). England: Horwood Publishing Ltd. Lege, J. (2005). Socrates meets the 21 st century. Teaching Mathematical Applications, 24(1), 29– 36. doi: 10. 1093/teamat/hrh 016 Lipowsky, F. (2006). Auf den Lehrer kommt es an. In Beiheft der Zeitschrift für Padagogik, 51 (pp. 47– 70). Beiheft. Weinheim: Beltz. Maa. B, K. (2005). Barriers and opportunities for the integration of modelling in mathematics classes: results of an empirical study. Teaching Mathematics and Its Applications, 24(2 -3), 61– 74. Maa. B, K. (2006). What are modelling competencies? Zentralblatt fur Didaktik der Mathematik 38(2), 113– 142. Martinez-Luaces, V. (2009). Modelling and inverse-modelling: experiences with O. D. E. linear systems in engineering courses. International Journal of Mathematical Education in Science and Technology, 40 (2), 259– 268. doi: 10. 1080/00207390802276291 Maull, W. & Berry, J. (2001). An investigation of student working styles in a mathematical modelling activity. Teaching Mathematics and its Applications, 20 (2), 78– 88. Niss, M. (2001). Issues and problems of research on the teaching and learning of applications and modelling. In Matos, J. , Houston, S. , Blum, W. & Carreira, S. (Eds). Modelling and Mathematics Education: ICTMA 9 - Applications in Science and Technology (pp. 381– 390). England: Horwood Publishing Ltd. Oke, K. (1984). Mathematical Modelling Processes: Implications for Teaching (Unpublished doctoral thesis). Loughborough University of Technology, Leicestershire, United Kingdom.

� � � � Palm, T. (2007). Features and impact of authenticity of applied mathematical school tasks. In Blum, W. , Glabraith, P. , Henn, H & Niss, M (Eds) Modelling and Applications in Mathematics Education (pp. 201– 208). New York, NY: Springer. Rowland, D. & Jovanoski, Z. (2004). Student interpretations of the terms in first-order ordinary differential equations in modelling contexts. International Journal of Mathematical Education in Science and Technology, 35(4), 503– 516. doi: 10. 1080/00207390410001686607 Rowland, D. (2004). Student difficulties with units in differential equations in modelling contexts. International Journal of Mathematical Education in Science and Technology, 37(5), 553– 558. doi: 10. 1080/00207390600597690 Schaap, S. , Vos, P. & Goedhart, M. (2011). Students Overcoming Blockages While Building a Mathematical Model: Exploring a Framework. In Kaiser et al (Eds) Trends in Teaching and Learning of Mathematical Modelling. (pp. 137– 146). New York, NY: Springer. Simon, M, A. (1995). Reconstructing Mathematics Pedagogy from a Constructivist Perspective. Journal for Research in Mathematics Education 26, 114– 145. Spooner, K. (2012). A Glimpse of Reality. Unpublished master’s thesis, University of Auckland, New Zealand. Spooner, K. (2014). Preliminaries for a first year course on Modelling. Proceedings of The Future of Mathematics Education in a Connected World Conference. (6 pages). Retrieved from http: //directorymathsed. net/montenegro/ Stillman, G. , Brown, J. & Galbraith, P. (2010). Identifying Challenges within Transition Phases of Mathematical Modeling Activities at Year 9. In Lesh, R. et al (Eds). Modeling Students Mathematical Modeling Competencies (pp. 385– 398). New York, NY: Springer. Stillman, G. (2004). Strategies employed by upper secondary students for overcoming or exploiting conditions affecting accessibility of applications tasks. Mathematics Education Research Journal, 16 (1), 41– 71. doi: 10. 1007/BF 03217390 Soon, W. , Tirtasanjaya Lioe, L. , & Mc. Innes, B. (2011). Understanding the difficulties faced by engineering undergraduates in learning mathematical modelling. International Journal of Mathematical Education in Science and Technology, 42 (8), 1032– 1039. doi: 10. 1080/0020739 X. 2011. 573867 Tam, K. C. (2011). Modelling in the Common Core Standards. Journal of Mathematics Education at Teachers College Spring-Summer 2011(2), 28– 33. Treilibs, V. , Burkhardt, H. , & Low, B. (1980). Formulation Processes in Mathematical modelling. Nottingham, UK: Shell Centre for Mathematical Education. Verschaffel, L. , Greer, B. & De. Corte, E. (2000). Making sense of word problems. Netherlands Lisse, The Netherlands: Swets & Zeitlinger. Wake, G. (2011). The Process of Mathematical Modelling. Course notes 160. 319 Mathematical Modelling. Albany: Massey University. Wake, G. (1997). Hi-tech Angles: Mathematics at Work. NZ Science Review 54 (1 -2), 5– 9.