Teaching Modules for Steel Instruction Combined Load Member

Teaching Modules for Steel Instruction Combined Load Member Design Developed by Scott Civjan University of Massachusetts, Amherst 1

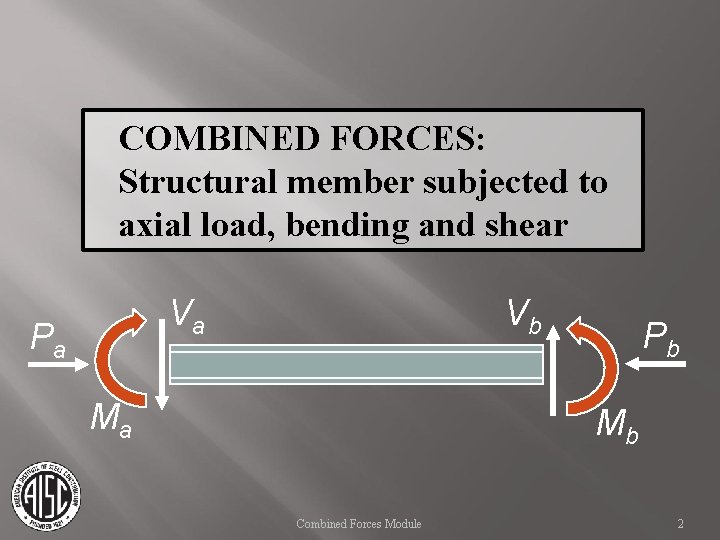
COMBINED FORCES: Structural member subjected to axial load, bending and shear Va Pa Vb Ma Pb Mb Combined Forces Module 2

Combined Forces: Chapter H: Chapter C: Appendix 7: Appendix 8: Chapter B: Part 6: Combined Forces Direct Analysis Method Other Analysis Requirements Alternative Analysis Methods Approximate 2 nd Order Analysis Local Buckling Classification Design Tables Combined Forces – AISC Manual 15 th Ed 3

COMBINED FORCES: Combinations of flexural and axial forces need to be addressed in both analysis and design. Analysis needs to consider second order effects (analysis based on final deformations). Design needs to consider combinations of forces in a member. Combined Forces Module 4

COMBINED FORCES: Major Issues to Address: Combination of multiple states of stress. Second order load effects. Direct analysis versus traditional K methods. Combined Forces Theory 5

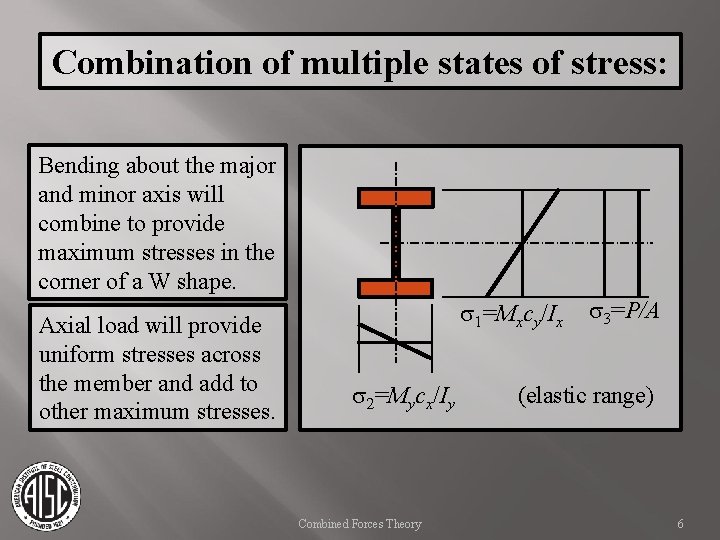
Combination of multiple states of stress: Bending about the major and minor axis will combine to provide maximum stresses in the corner of a W shape. Axial load will provide uniform stresses across the member and add to other maximum stresses. s 1=Mxcy/Ix s 2=Mycx/Iy Combined Forces Theory s 3=P/A (elastic range) 6

Combination of multiple states of stress Bending in each direction occurs simultaneously with associated shear stresses. For elastic analysis one can superimpose stresses and arrive at a maximum value. Actual design may include inelastic behavior and needs to account for residual stresses. Once behavior becomes inelastic the resulting stresses are very difficult to calculate. Combined Forces Theory 7

Combination of multiple states of stress Design provisions are simplified and rely on the inherent ductility of steel to redistribute stresses throughout the section. The basic principle for design is an interaction equation which combines axial and bending forces with shear being checked independently. Modes of failure from all independent modes are analyzed independently of other modes and forces. This does not capture complete behavior, but is sufficiently accurate for design purposes. Combined Forces Theory 8

DIRECT ANALYSIS OR “TRADITIONAL” METHODS Analysis methods and design calculations are determined by the method used. Direct Analysis applies additional “notional” loads and reduced member stiffness but uses K = 1 in column design. Traditional method uses “notional” loads, calculated K values (alignment chart) in column design and nominal stiffness properties. Combined Forces Module 9

Combined Forces Analysis and Design Direct Analysis Method (C 1. 1) or traditional methods (Appendix 7) may be used, but analysis and design must be consistent with the single approach chosen. Interaction Equations of Chapter H are applied for member design acceptance. Values used in these equations must be consistent with the analysis and design method used. Combined Forces – AISC Manual 15 th Ed 10

Doubly and Singly Symmetric Members: Flexure and Compression Combined Forces – AISC Manual 15 th Ed 11

Combination of multiple states of stress: Design provisions are simplified and rely on the inherent ductility of steel to redistribute forces throughout the section. The basic principle for design is an interaction equation which combines forces from axial and bending loads. Shear is checked independently. Modes of failure from all independent modes are analyzed independently of other modes and forces. This is not completely realistic, but is sufficiently accurate for design purposes. Combined Forces – AISC Manual 15 th Ed 12

Doubly and Singly Symmetric Members: Flexure and Compression For Equation H 1 -1 a Equation H 1 -1 b For Combined Forces – AISC Manual 15 th Ed 13

Doubly and Singly Symmetric Members: Flexure and Compression Pr = required axial compressive strength from 2 nd ORDER ANALYSIS (from LRFD load combinations). Pc = available design axial compressive strength per LRFD (strength from Chapter E). Mr = required flexural strength from 2 nd ORDER ANALYSIS (from LRFD load combinations). Mc = available design flexural strength per LRFD (strength from Chapter F). x = strong axis bending y = weak axis bending Combined Forces – AISC Manual 15 th Ed 14

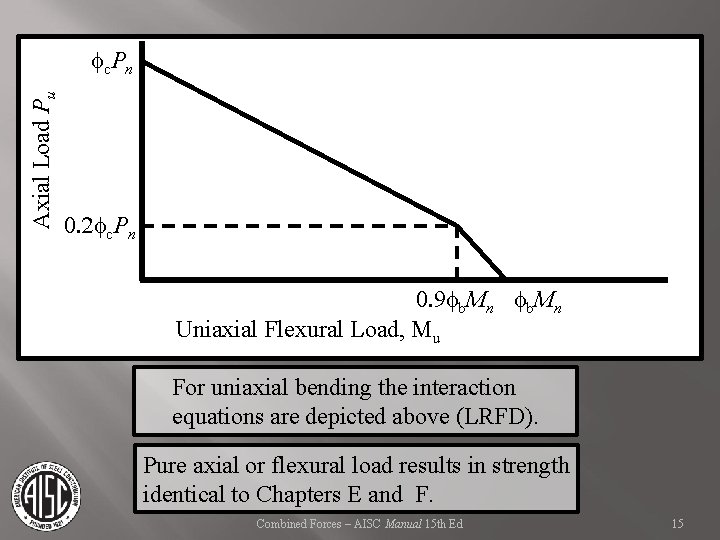
Axial Load Pu f c. P n 0. 2 fc. Pn 0. 9 fb. Mn Uniaxial Flexural Load, Mu For uniaxial bending the interaction equations are depicted above (LRFD). Pure axial or flexural load results in strength identical to Chapters E and F. Combined Forces – AISC Manual 15 th Ed 15

Doubly and Singly Symmetric Members: Flexure and Tension Combined Forces – AISC Manual 15 th Ed 16

Doubly and Singly Symmetric Members: Flexure and Tension The same equations are used for tension and compression. (H 1 -1 a and H 1 -1 b) Substitute: Pr = required axial tensile strength (from LRFD load combinations) Pc = available design axial tensile strength per LRFD (strength from Chapter D) Additionally, for Mc Cb can be increased per Section H 1. 2. Lateral torsional buckling design strength increases due to tension. Combined Forces – AISC Manual 15 th Ed 17

Analysis Requirements of AISC Combined Forces – AISC Manual 15 th Ed 18

Combined Forces Analysis and Design Second order analysis is required per C 1. Any rational method that accounts for both P-D and P-d is acceptable. Geometric imperfections shall be considered. Second order analysis for LRFD uses load combinations. Combined Forces – AISC Manual 15 th Ed 19

Combined Forces Analysis and Design Typically computer analysis is used to calculate second order effects. Many programs neglect P-d analysis. Often not a significant effect, but this should be checked. P-d analysis can be neglected if requirements of Section C 2. 1(b) are met. Combined Forces – AISC Manual 15 th Ed 20

Combined Forces Analysis and Design Initial imperfections must be considered, either through application of notional loads or direct modeling. Notional loads are applied to all load cases (Section C 2. 2 b(1)) unless second order to first order drift ratio is ≤ 1. 7. Then can apply notional loads only to gravity load combinations (Section C 2 -2 b(d)). This last provision is applicable to the “traditional” method restrictions, therefore often requires the application of notional loads in fewer cases than the direct analysis method. Combined Forces – AISC Manual 15 th Ed 21

Combined Forces Application of notional loads (Section C 2 -2 b). Ni = 0. 002 Yi Ni = notional lateral load applied at level i Yi = gravity load at level i from load combinations Consider independently in two orthogonal directions. This load accounts for assumed out-of-plumbness of 1/500, satisfying consideration of geometric imperfections in the analysis. Combined Forces – AISC Manual 15 th Ed 22

Chapter C: Direct Analysis Method Combined Forces – AISC Manual 15 th Ed 23

Direct Analysis Method Analysis REQUIRED if D 2 nd Order/D 1 st Order > 1. 5 (B 2 > 1. 5) (Section Appendix 7. 2. 1) K = 1 for all design Second order analysis (P-d and P-D) required, such as verified computer analysis or amplified first order analysis. Combined Forces – AISC Manual 15 th Ed 24

Direct Analysis Method Reduce Stiffness EI* and EA* per Section C 2. 3: Stiffness adjustments are applied to all components that contribute to the stability of the structure (Section C 2. 3) Stability is typically affected by flexural stiffness of members in moment frames and axial stiffness of braced frame components. Combined Forces – AISC Manual 15 th Ed 25

Direct Analysis Method Reduce Stiffness EI* per Section C 2. 3: EI* = 0. 8 tb. EI. E = modulus of elasticity I = moment of inertia about axis of bending tb = reduction factor for inelastic action Required for all members that contribute to lateral stability of the structure (safe to include for all members). Combined Forces – AISC Manual 15 th Ed 26

Direct Analysis Method Reduce Stiffness EI* per Section C 2. 3: tb = Reduction Factor for Inelastic Action for Equations C 2 -2 a and C 2 -2 b Pr = required axial compressive strength Py = Fy. A = member yield strength a = 1. 0 (LRFD), 1. 6 (ASD) Combined Forces – AISC Manual 15 th Ed 27

Direct Analysis Method Reduce Stiffness EI* per Section C 2. 3: If an additional notional load of Ni = 0. 001 a. Yi is applied at all levels in all load combinations (even if Section C 2. 2 b(d) applies), tb = 1 per Section C 2. 3(c) Therefore, all stiffness could be adjusted similarly Combined Forces – AISC Manual 15 th Ed 28

Direct Analysis Method Reduce Stiffness EA* per Section C 2. 3: EA* = 0. 8 EA E = modulus of elasticity A = cross sectional member area Required for all members that contribute to lateral stability of the structure (safe to include for all members). Combined Forces – AISC Manual 15 th Ed 29

Chapter B: Local Buckling Criteria Combined Forces – AISC Manual 15 th Ed 30

Local Buckling Criteria Defined in Table B 4. 1 Since members are analyzed independently under flexural and axial loads, the local buckling provisions are checked separately for use in calculations related to each member type. This does not directly address the combination of stresses which may make web local buckling less likely to occur for some load conditions. Combined Forces – AISC Manual 15 th Ed 31

nd 2 Order Effects Theory Combined Forces – AISC Manual 15 th Ed 32

Second Order Effects Equilibrium is based on DEFORMED GEOMETRY. Initially, consider a member subjected to flexure only. Combined Forces Theory 33

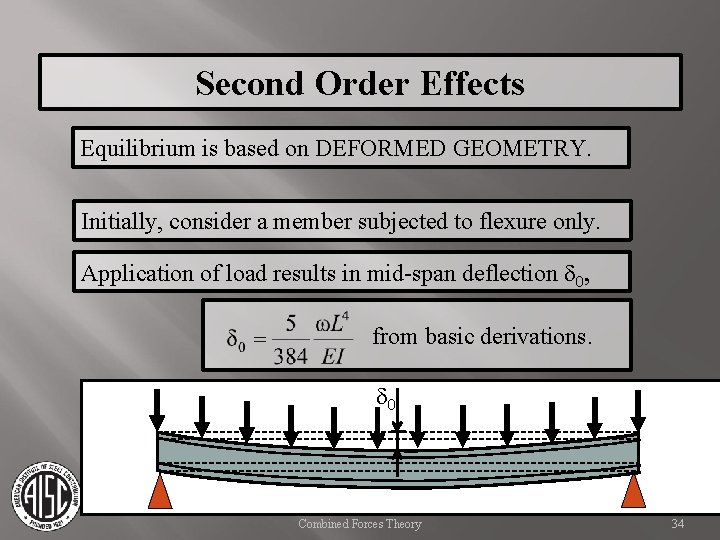
Second Order Effects Equilibrium is based on DEFORMED GEOMETRY. Initially, consider a member subjected to flexure only. Application of load results in mid-span deflection d 0, from basic derivations. d 0 Combined Forces Theory 34

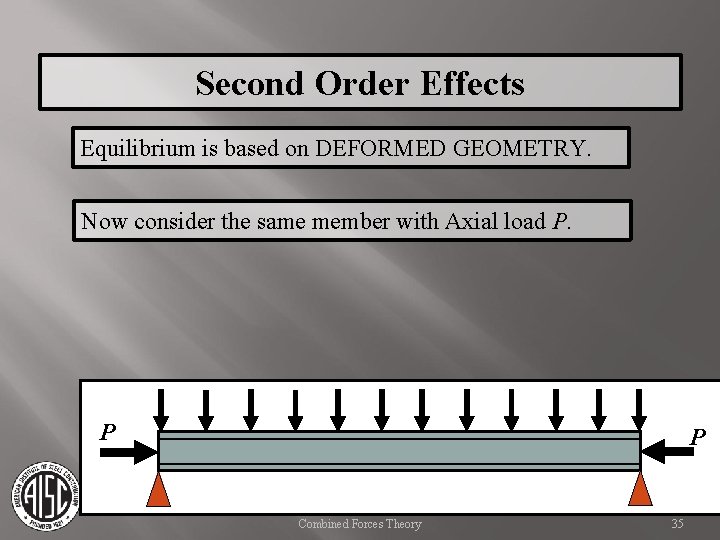
Second Order Effects Equilibrium is based on DEFORMED GEOMETRY. Now consider the same member with Axial load P. P P Combined Forces Theory 35

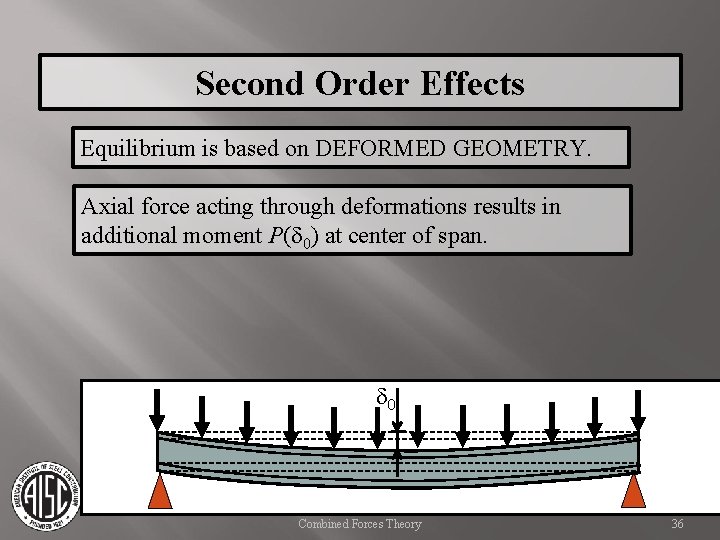
Second Order Effects Equilibrium is based on DEFORMED GEOMETRY. Axial force acting through deformations results in additional moment P(d 0) at center of span. d 0 Combined Forces Theory 36

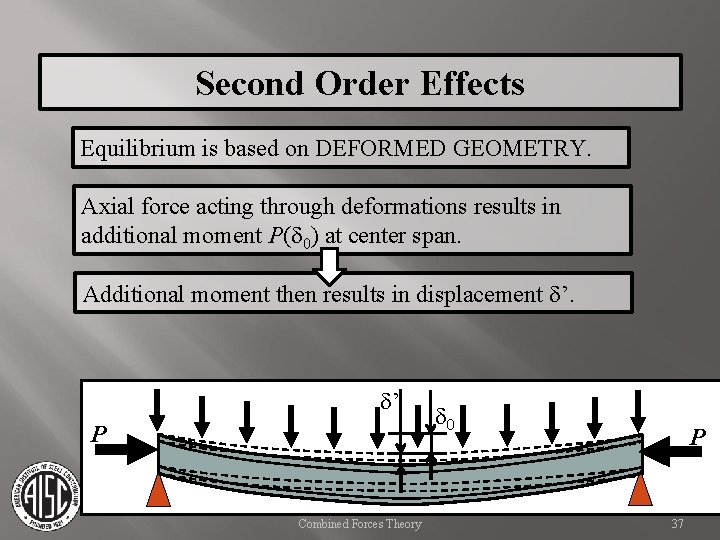
Second Order Effects Equilibrium is based on DEFORMED GEOMETRY. Axial force acting through deformations results in additional moment P(d 0) at center span. Additional moment then results in displacement d’. d’ P Combined Forces Theory d 0 P 37

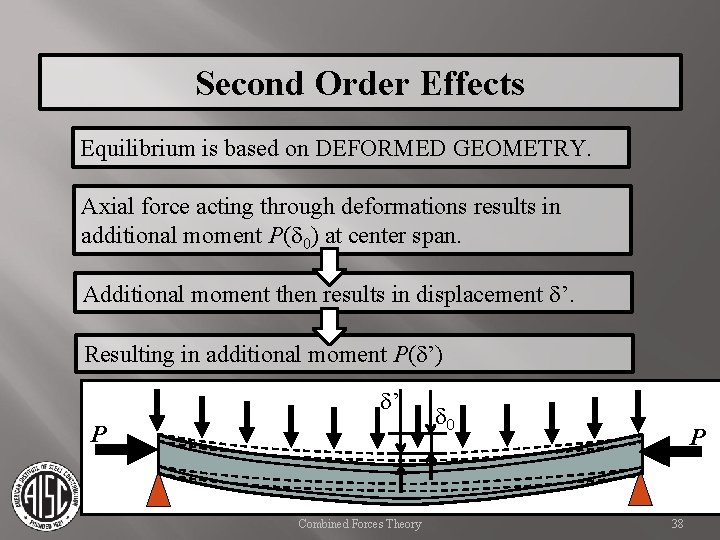
Second Order Effects Equilibrium is based on DEFORMED GEOMETRY. Axial force acting through deformations results in additional moment P(d 0) at center span. Additional moment then results in displacement d’. Resulting in additional moment P(d’) d’ P Combined Forces Theory d 0 P 38

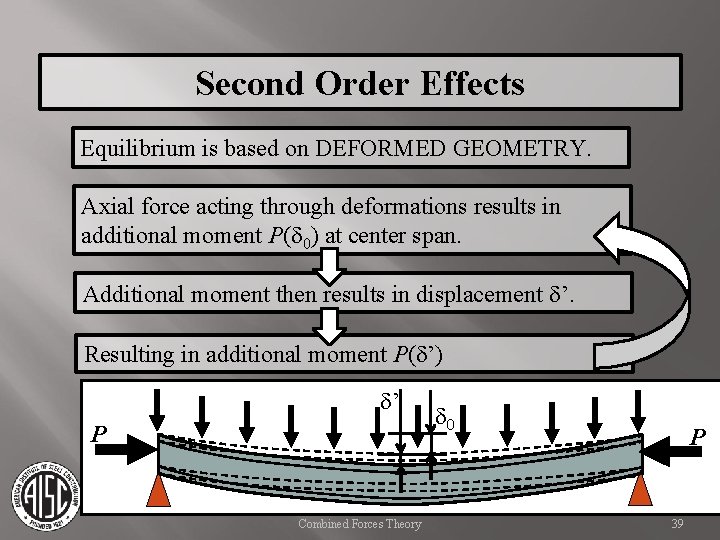
Second Order Effects Equilibrium is based on DEFORMED GEOMETRY. Axial force acting through deformations results in additional moment P(d 0) at center span. Additional moment then results in displacement d’. Resulting in additional moment P(d’) d’ P Combined Forces Theory d 0 P 39

Second Order Effects Equilibrium is based on DEFORMED GEOMETRY. This either results in an incremental failure, or stabilizes. d > d 0 and M > M 0 where d 0 and M 0 are first order results based on original geometry. M = M 0 + Pd but d depends on M… Combined Forces Theory 40

Second Order Effects When considering a frame with loads applied at joints the same principles can be applied. In these cases, we define joint deflections as D, with D 0 being the first order joint deflection. Combined Forces Theory 41

Second Order Effects P P Combined Forces Theory 42

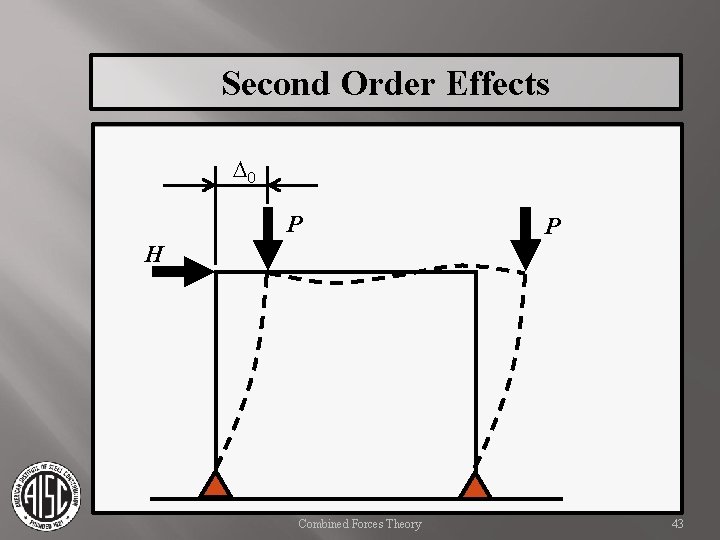
Second Order Effects D 0 P P H Combined Forces Theory 43

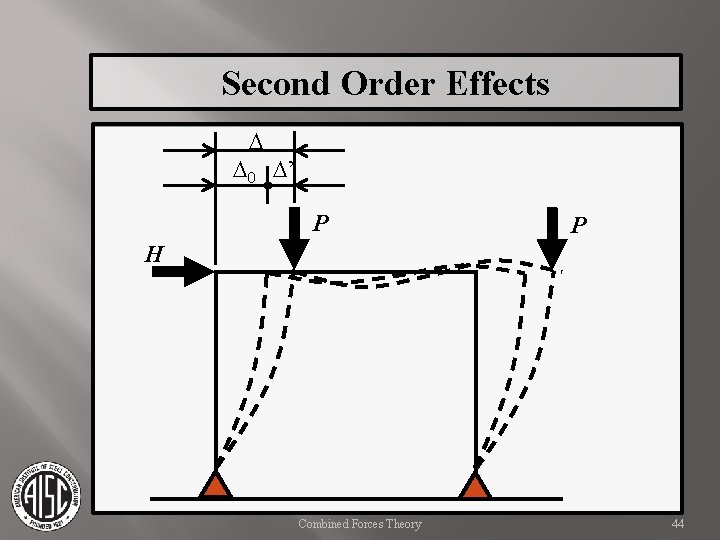
Second Order Effects D D 0 D’ P P H Combined Forces Theory 44

Second Order Effects Tension forces and Flexure Tension forces on a member tend to “straighten” the member. They do not introduce 2 nd order effects. Multiple states of stress are still present and need to be accounted for. Tension in a member can also make lateral torsional buckling less likely to occur. Combined Forces Theory 45

Second Order Effects INDIVIDUAL MEMBERS 2 nd Order Analysis Theory Combined Forces Theory 46

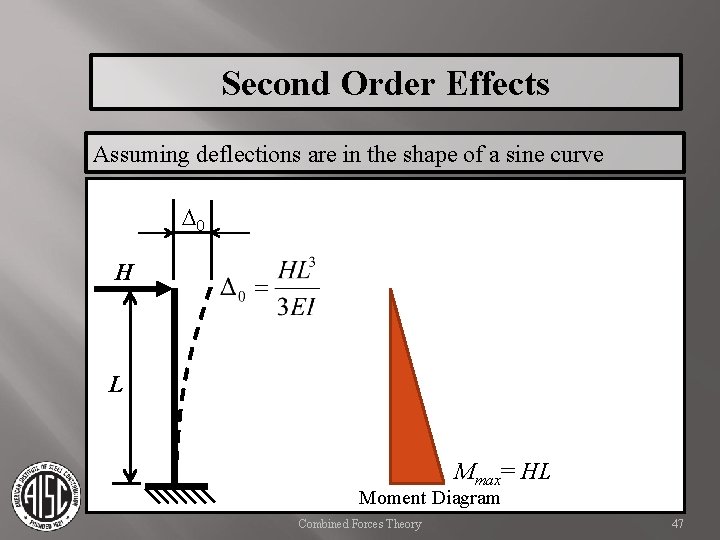
Second Order Effects Assuming deflections are in the shape of a sine curve D 0 H L Mmax= HL Moment Diagram Combined Forces Theory 47

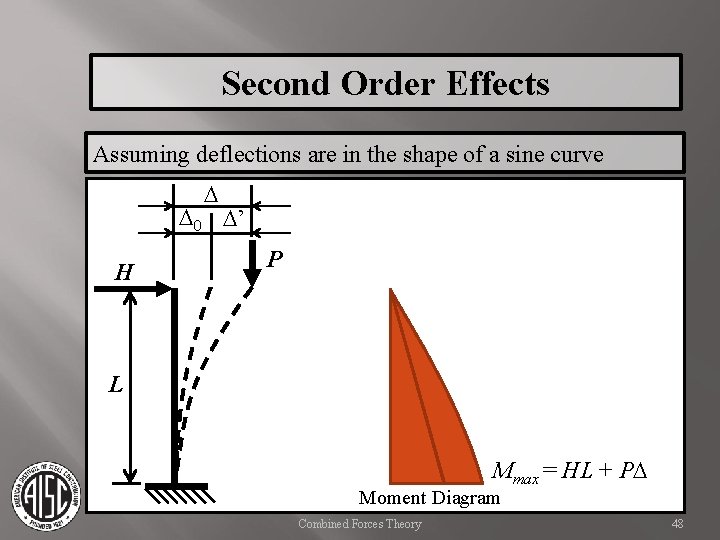
Second Order Effects Assuming deflections are in the shape of a sine curve D D 0 D’ H P L Mmax = HL + PD Moment Diagram Combined Forces Theory 48

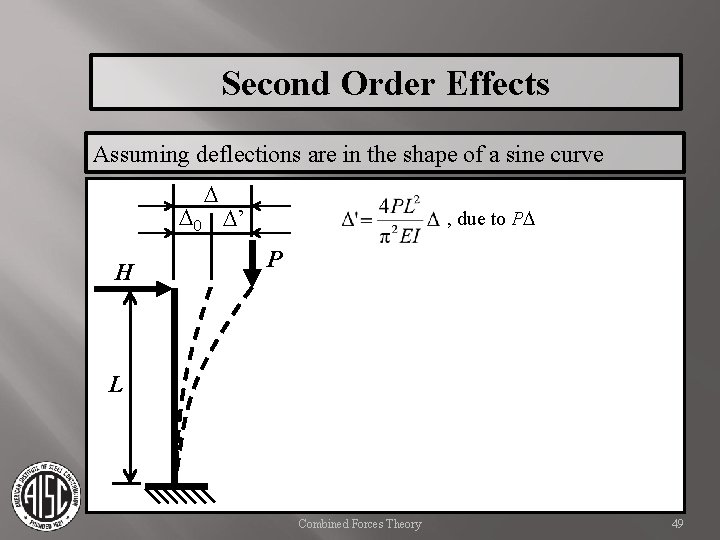
Second Order Effects Assuming deflections are in the shape of a sine curve D D 0 D’ H , due to PD P L Combined Forces Theory 49

Second Order Effects Assuming deflections are in the shape of a sine curve D D 0 D’ H , due to PD P L Combined Forces Theory 50

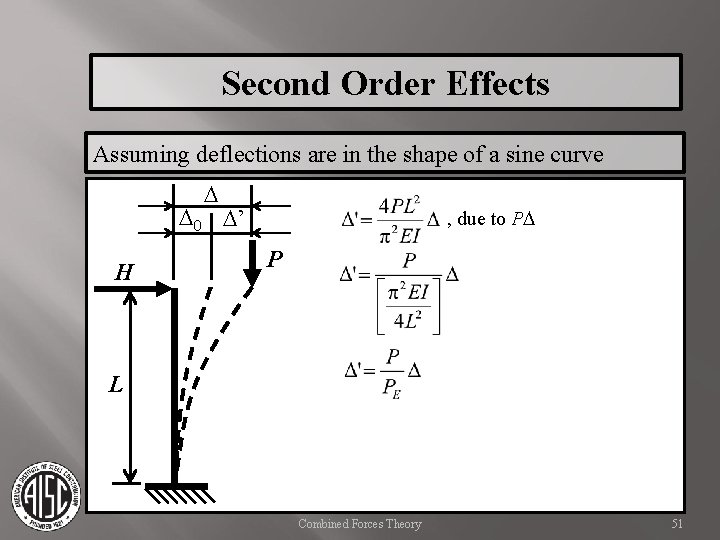
Second Order Effects Assuming deflections are in the shape of a sine curve D D 0 D’ H , due to PD P L Combined Forces Theory 51

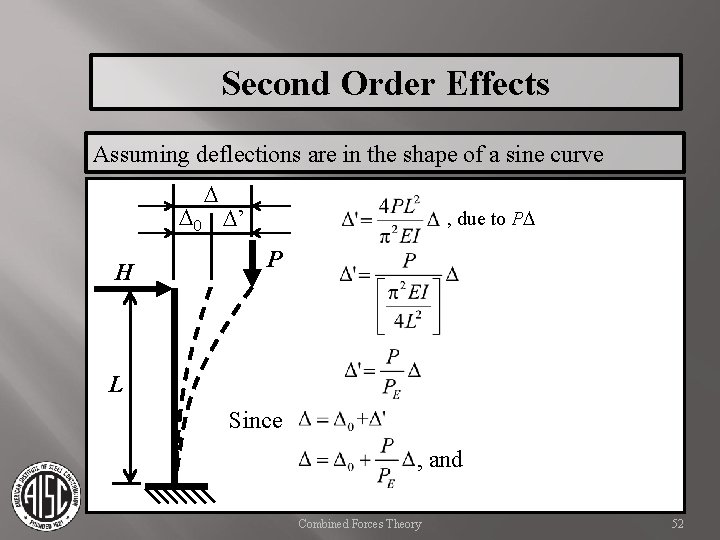
Second Order Effects Assuming deflections are in the shape of a sine curve D D 0 D’ H , due to PD P L Since , and Combined Forces Theory 52

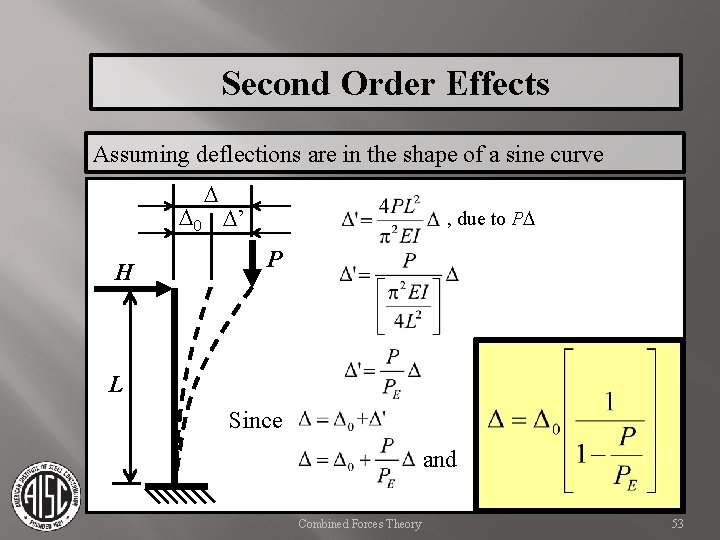
Second Order Effects Assuming deflections are in the shape of a sine curve D D 0 D’ H , due to PD P L Since and Combined Forces Theory 53

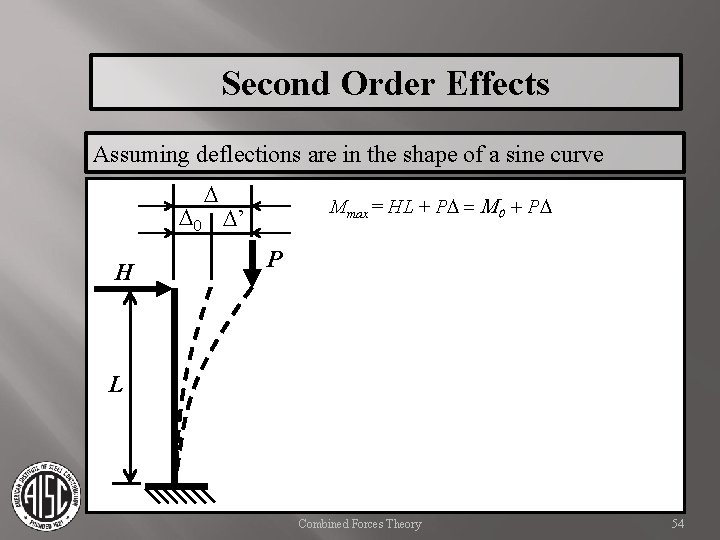
Second Order Effects Assuming deflections are in the shape of a sine curve D Mmax = HL + PD = M 0 + PD D 0 D’ H P L Combined Forces Theory 54

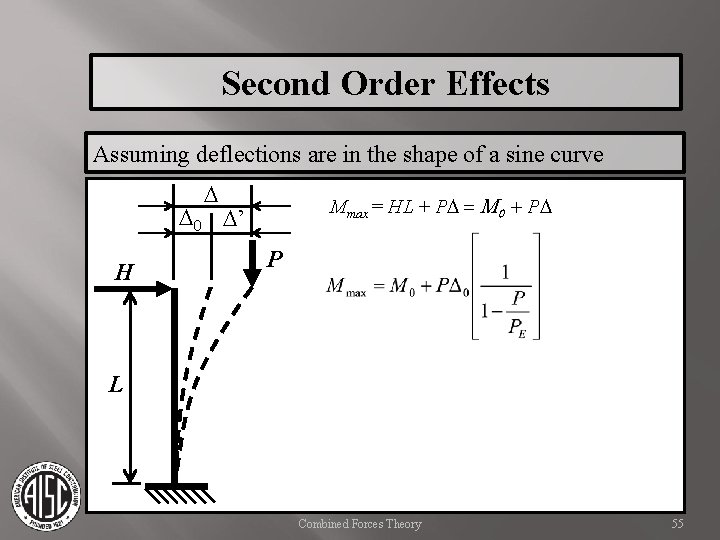
Second Order Effects Assuming deflections are in the shape of a sine curve D Mmax = HL + PD = M 0 + PD D 0 D’ H P L Combined Forces Theory 55

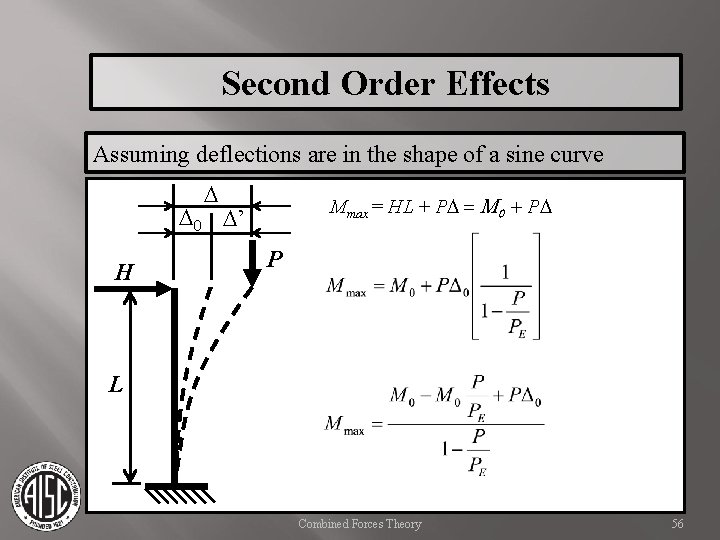
Second Order Effects Assuming deflections are in the shape of a sine curve D Mmax = HL + PD = M 0 + PD D 0 D’ H P L Combined Forces Theory 56

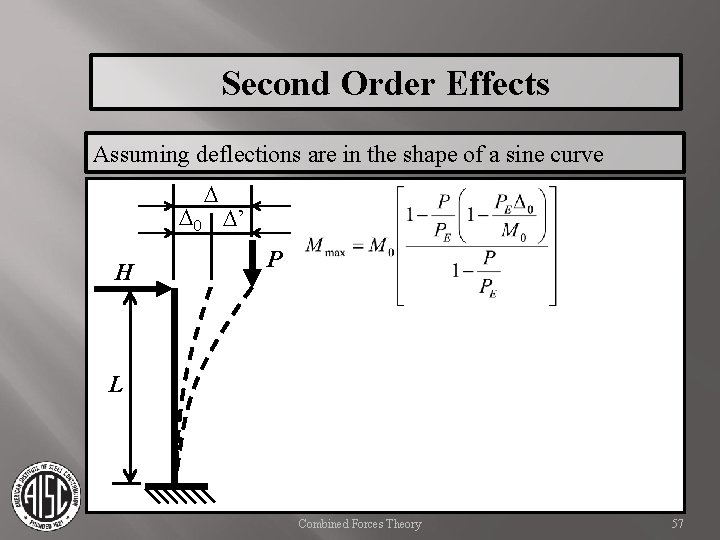
Second Order Effects Assuming deflections are in the shape of a sine curve D D 0 D’ H P L Combined Forces Theory 57

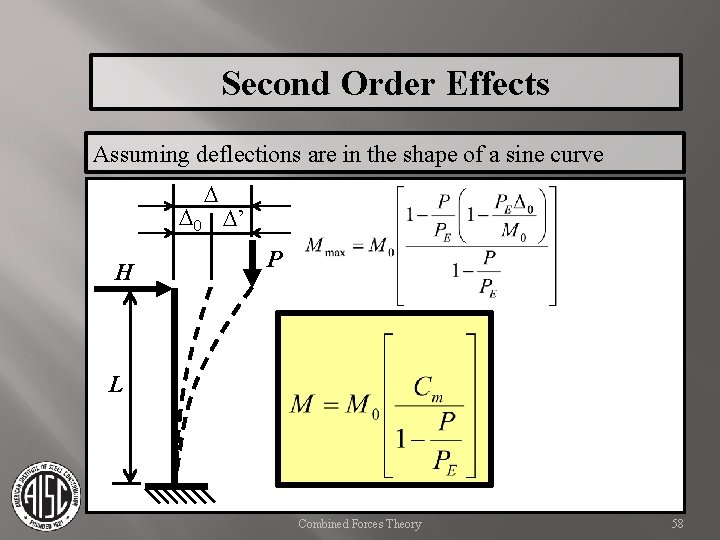
Second Order Effects Assuming deflections are in the shape of a sine curve D D 0 D’ H P L Combined Forces Theory 58

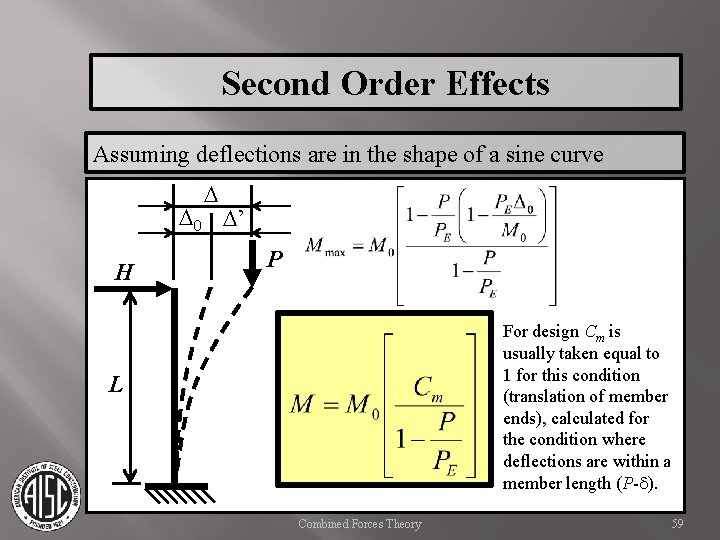
Second Order Effects Assuming deflections are in the shape of a sine curve D D 0 D’ H P For design Cm is usually taken equal to 1 for this condition (translation of member ends), calculated for the condition where deflections are within a member length (P-d). L Combined Forces Theory 59

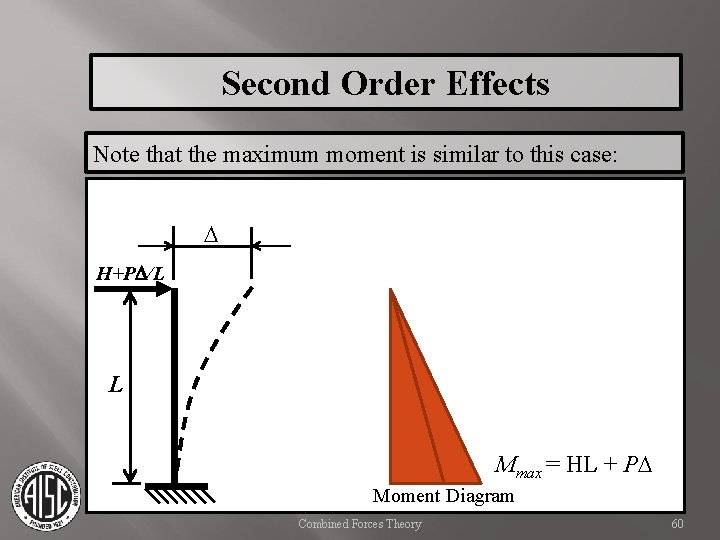
Second Order Effects Note that the maximum moment is similar to this case: D H+PD/L L Mmax = HL + PD Moment Diagram Combined Forces Theory 60

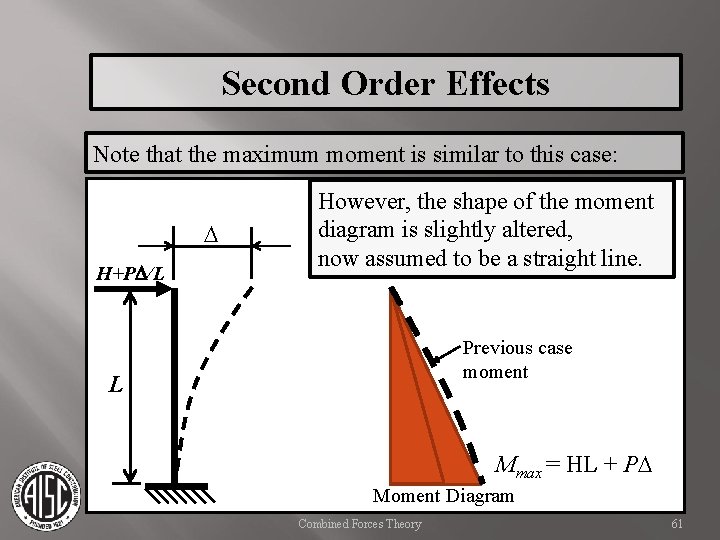
Second Order Effects Note that the maximum moment is similar to this case: D H+PD/L However, the shape of the moment diagram is slightly altered, now assumed to be a straight line. Previous case moment L Mmax = HL + PD Moment Diagram Combined Forces Theory 61

Second Order Effects Note that the maximum moment is similar to this case: D H+PD/L L Combined Forces Theory 62

Second Order Effects Note that the maximum moment is similar to this case: D H+PD/L L Combined Forces Theory 63

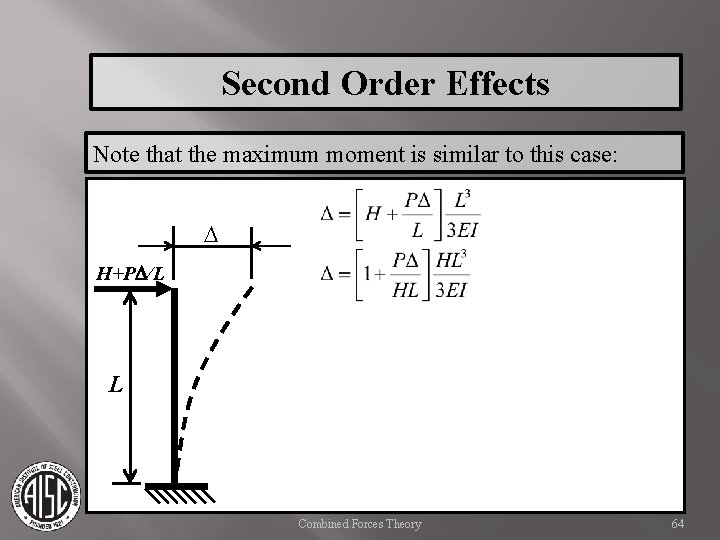
Second Order Effects Note that the maximum moment is similar to this case: D H+PD/L L Combined Forces Theory 64

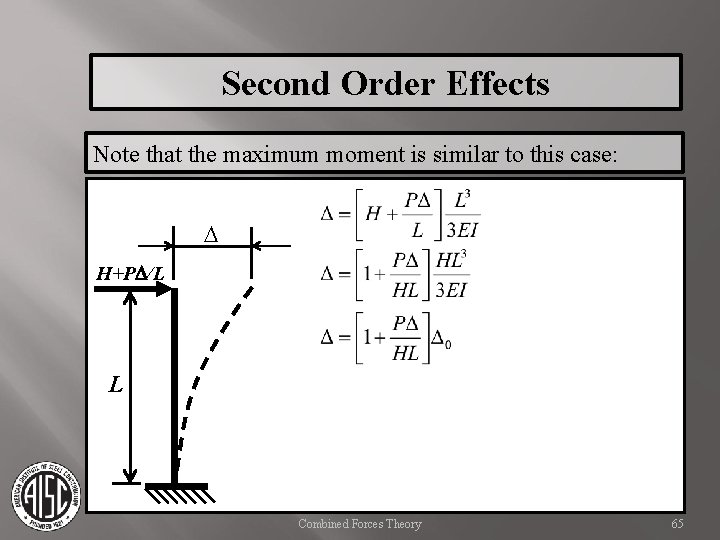
Second Order Effects Note that the maximum moment is similar to this case: D H+PD/L L Combined Forces Theory 65

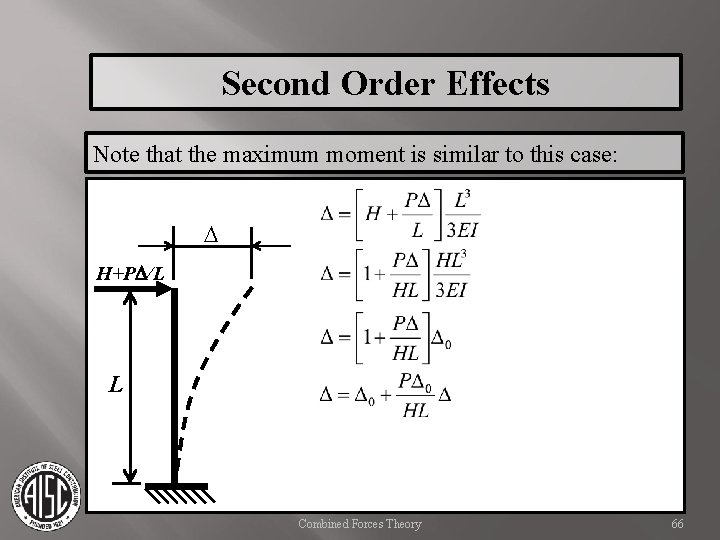
Second Order Effects Note that the maximum moment is similar to this case: D H+PD/L L Combined Forces Theory 66

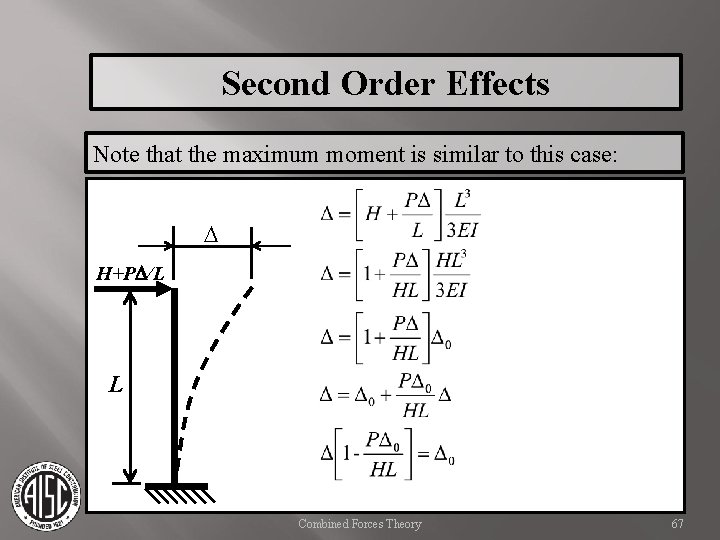
Second Order Effects Note that the maximum moment is similar to this case: D H+PD/L L Combined Forces Theory 67

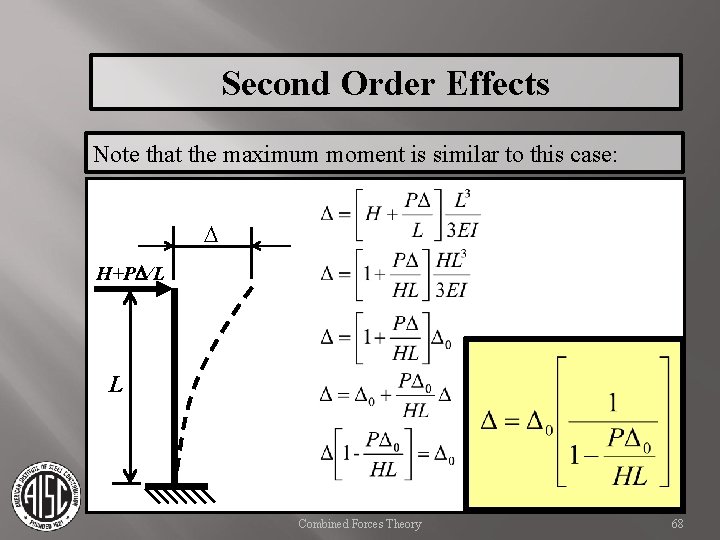
Second Order Effects Note that the maximum moment is similar to this case: D H+PD/L L Combined Forces Theory 68

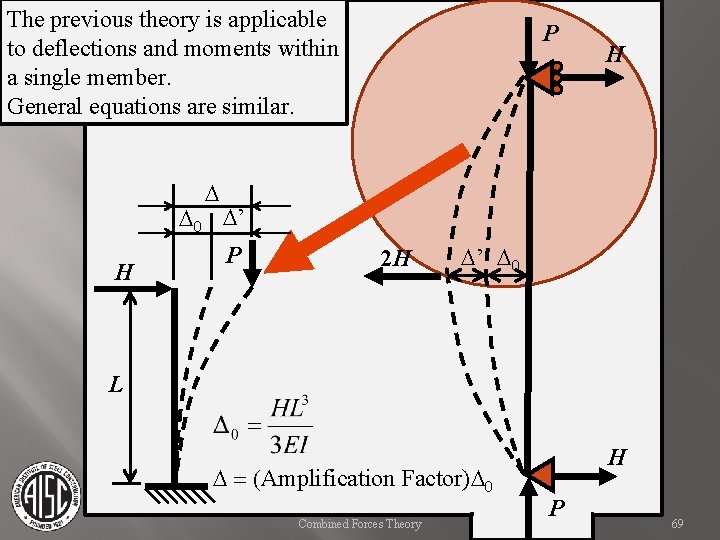
The previous theory is applicable to deflections and moments within a single member. General equations are similar. P H D D 0 D’ H P 2 H D’ D 0 L D = (Amplification Factor)D 0 Combined Forces Theory H P 69

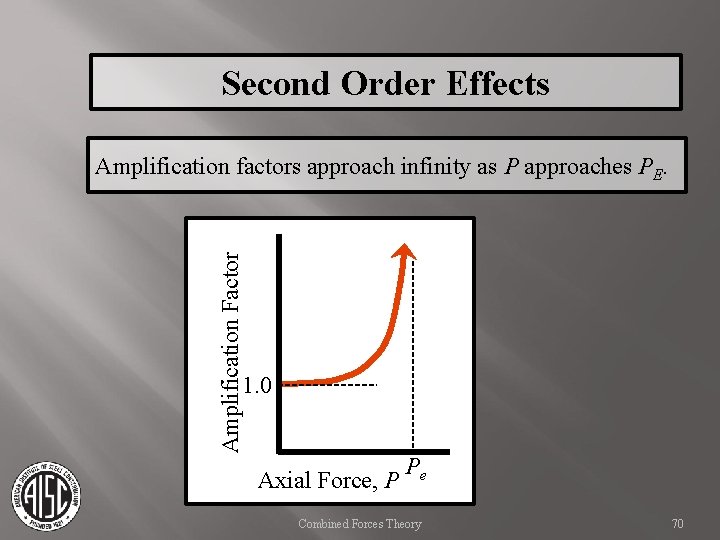
Second Order Effects Amplification Factor Amplification factors approach infinity as P approaches PE. 1. 0 Axial Force, P Pe Combined Forces Theory 70

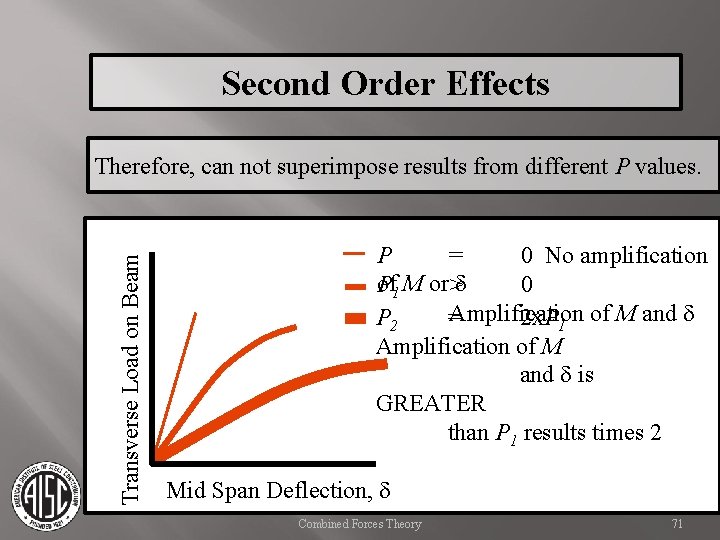
Second Order Effects Transverse Load on Beam Therefore, can not superimpose results from different P values. P = 0 No amplification of M or d P 1 > 0 P 2 =Amplification of M and d 2 x. P 1 Amplification of M and d is GREATER than P 1 results times 2 Mid Span Deflection, d Combined Forces Theory 71

Second Order Effects MEMBERS WITHIN STRUCTURE Combined Forces Theory 72

Second Order Effects Note that in a full structure all displacements within a story are similar. P 1 P 2 P 3 P 4 H L Combined Forces Theory 73

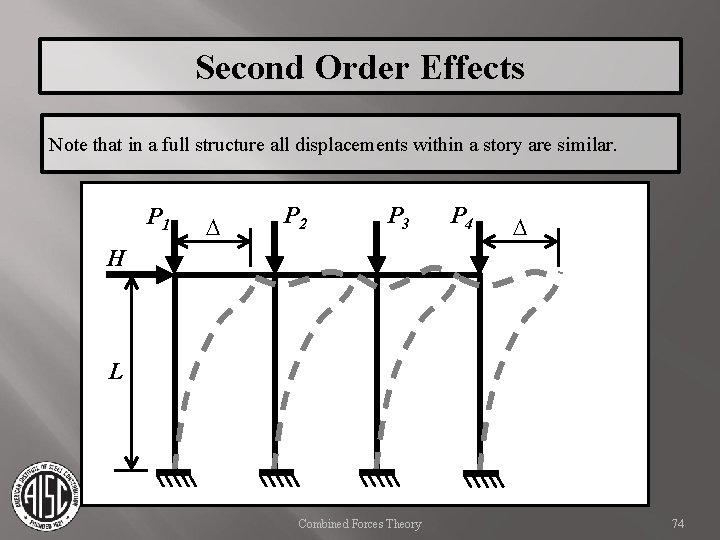
Second Order Effects Note that in a full structure all displacements within a story are similar. P 1 D P 2 P 3 P 4 D H L Combined Forces Theory 74

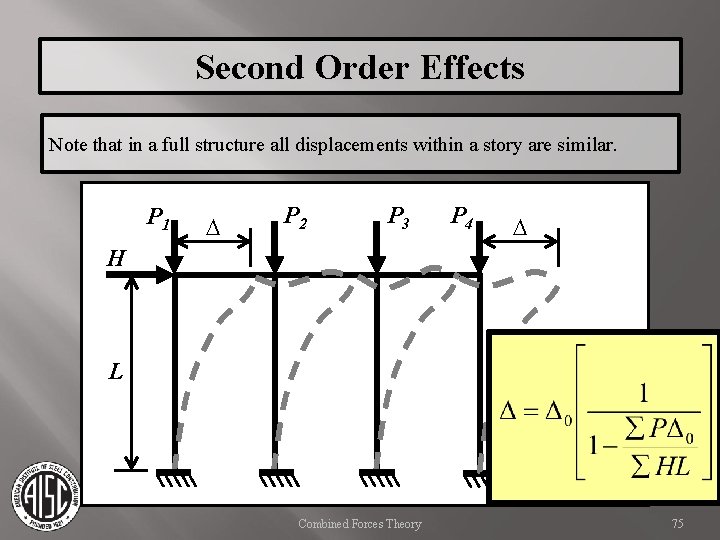
Second Order Effects Note that in a full structure all displacements within a story are similar. P 1 D P 2 P 3 P 4 D H L Combined Forces Theory 75

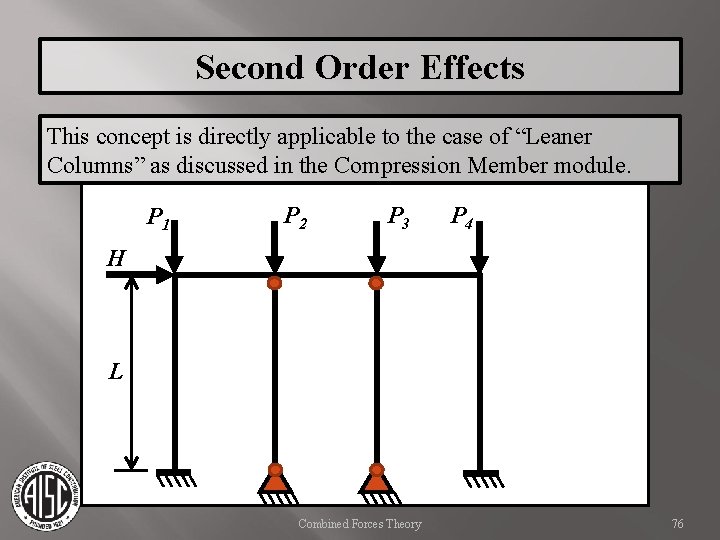
Second Order Effects This concept is directly applicable to the case of “Leaner Columns” as discussed in the Compression Member module. P 1 P 2 P 3 P 4 H L Combined Forces Theory 76

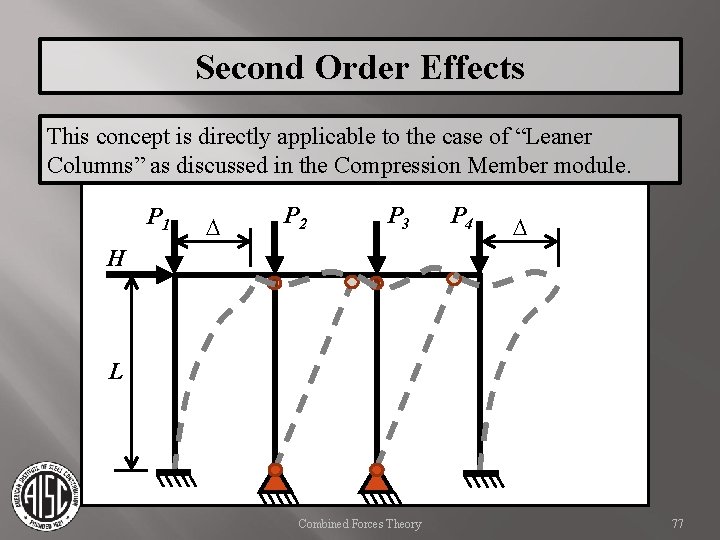
Second Order Effects This concept is directly applicable to the case of “Leaner Columns” as discussed in the Compression Member module. P 1 D P 2 P 3 P 4 D H L Combined Forces Theory 77

NOTIONAL LOADS Combined Forces Theory 78

NOTIONAL LOADS Notional loads are a function of the gravity load being applied. Notional loads are applied as a lateral load at each floor level in the direction that adds to the destabilizing effects of the load combination being considered. Notional loads can account for geometric imperfections, inelasticity of members, and other non-ideal conditions. Notional loads can be thought of as representing an initial out-of-plumbness in each story of the structure of 1/500 times the story height. Combined Forces Theory 79

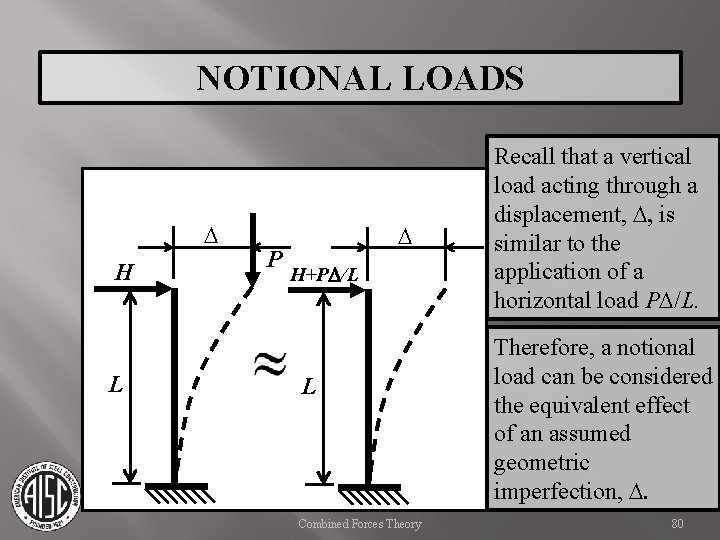
NOTIONAL LOADS D H L P D H+PD/L L Combined Forces Theory Recall that a vertical load acting through a displacement, D, is similar to the application of a horizontal load PD/L. Therefore, a notional load can be considered the equivalent effect of an assumed geometric imperfection, D. 80

MODELING ISSUES Combined Forces Theory 81

Second Order Effects Final deflections and moments can be calculated in several different ways. Closed form mathematical solutions: Derivations exist for standard results, but very difficult, if not impossible, for a full structure. Approximate Methods: Amplification factor applied to first order displacement and moments by simple method OR approximate computer methods will provide results within a given tolerance. Combined Forces Theory 82

Second Order Effects 2 nd order analysis is any method that accounts for P-D and P-d effects. Exact Closed-Form Solution Computer Analysis Amplified First Order Analysis Combined Forces Theory 83

Exact Closed-Form Solution Exact solutions for P-d and P-D can be derived for simple structures. For full structures typically encountered in design the process is generally too tedious to perform. Combined Forces Theory 84

Computer Analysis Most structural analysis programs will include some form of “second order” analysis. To satisfy a “rigorous 2 nd order analysis” a program must include both P-D and P-d analysis, or the designer must verify that P-d effects are minimal in the structure. Computers use approximate solutions rather than exact closed form solutions, and iterate until a specified error tolerance is reached. Combined Forces Theory 85

Computer Analysis Designers must verify that second order effects are correctly handled by the programs being used. Verify that load combinations include second order effects. Some programs analyze individual load cases only. Load case results are factored and summed to produce load combinations, but are not re-analyzed. Therefore, moments resulting from lateral loads in one load case may not be correctly amplified by axial load in a separate load case when combined in a load combination. Combined Forces Theory 86

Computer Analysis H Verify computer programs correctly analyze load combinations. Load Case 1 + P Load Case 2 Combined Forces Theory P 87

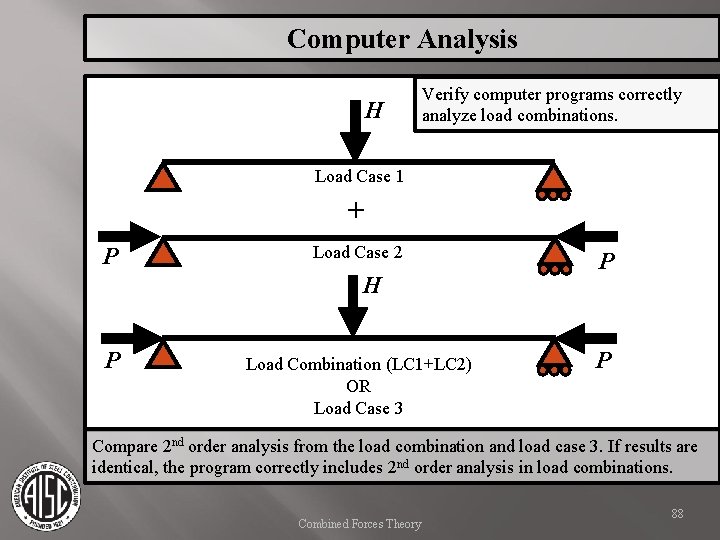
Computer Analysis H Verify computer programs correctly analyze load combinations. Load Case 1 + P Load Case 2 H P Load Combination (LC 1+LC 2) OR Load Case 3 P P Compare 2 nd order analysis from the load combination and load case 3. If results are identical, the program correctly includes 2 nd order analysis in load combinations. Combined Forces Theory 88

Computer Analysis Designers must verify that second order effects are correctly handled by the programs being used. Combined Forces Theory 89

Computer Analysis Designers must verify that second order effects are correctly handled by the programs being used To determine the capabilities of a specific program compare first and second order analysis results for known load cases – typically a flagpole (P-D) and simple beam (P-d) with axial and lateral loads applied. (Figures C-C 2. 2 and C-C 2. 3) Most programs only include P-D. If P-d effects are significant the designer can use multiple elements to provide equivalent P-D effects within the original element. Combined Forces Theory 90

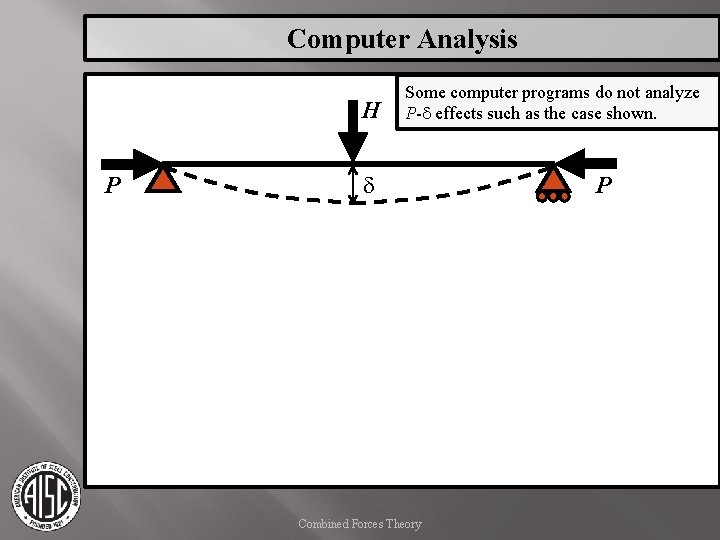
Computer Analysis H P Some computer programs do not analyze P-d effects such as the case shown. d Combined Forces Theory P

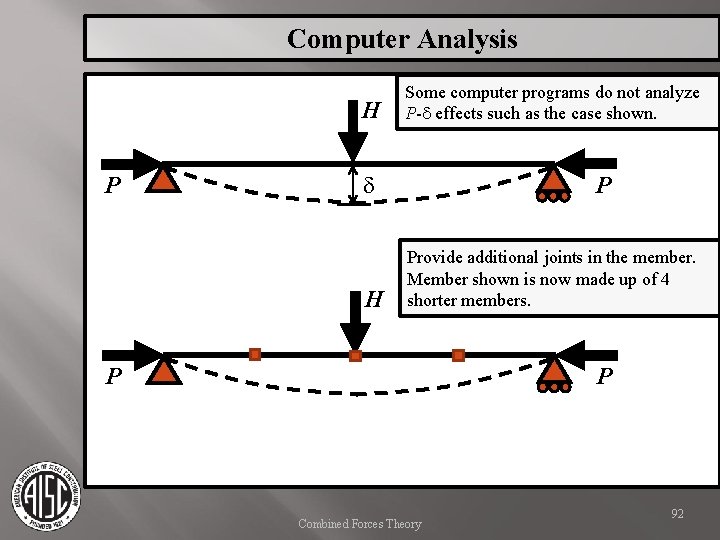
Computer Analysis H P Some computer programs do not analyze P-d effects such as the case shown. d H P Provide additional joints in the member. Member shown is now made up of 4 shorter members. P P Combined Forces Theory 92

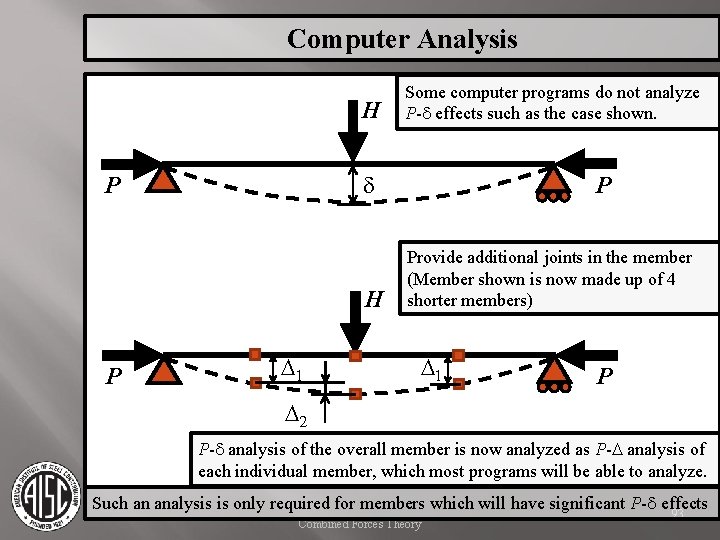
Computer Analysis H d P H P Some computer programs do not analyze P-d effects such as the case shown. D 1 P Provide additional joints in the member (Member shown is now made up of 4 shorter members) D 1 P D 2 P-d analysis of the overall member is now analyzed as P-D analysis of each individual member, which most programs will be able to analyze. Such an analysis is only required for members which will have significant P-d effects Combined Forces Theory 93

Combined Forces Braced frames with pinned member connections: If loads applied at the nodes, members are subjected to axial forces only. Beams and girders may be subjected to combined forces, but designers should take care in understanding whether analysis results represent compressive forces present in the steel section or carried by the floor slab. Combined Forces Theory 94

Combined Forces Moment frames with fixed member connections: Most if not all members will be subjected to a combination of axial forces, flexure and shear. Combined Forces Theory 95

Appendix 8: Approximate Second. Order Analysis Combined Forces – AISC Manual 15 th Ed 96

Amplified First Order Analysis Amplification of First-Order Elastic Analysis Appendix 8 This method is typically used in the following situations: To analyze and design simple structures being performed by hand calculations. To verify second order results in computer analyses. To determine the significance of P-d effects (B 1 factor). Basis for the factors is in 2 nd order analysis theory slides Combined Forces – AISC Manual 15 th Ed 97

Amplified First Order Analysis Mr = B 1 Mnt + B 2 Mlt Equation A-8 -1 Mr = second order required flexural strength B 1 = amplification factor to account for second order effects caused by displacements along member length (P-d effects). Mnt = first order moment, assuming no lateral translation of frame (from load combinations). B 2 = amplification factor to account for second order effects caused by displacements of member ends (P-D effects). Mlt = first order moment caused by lateral translation of frame (from load combinations). Combined Forces – AISC Manual 15 th Ed 98

Amplified First Order Analysis Pr = Pnt + B 2 Plt Equation A-8 -2 Pr = second order required axial strength. Pnt = first order axial force, assuming no lateral translation of frame (from load combinations). B 2 = amplification factor to account for second order effects caused by displacements of member ends (P-D effects). Plt = first order axial force caused by lateral translation of frame (from load combinations). Combined Forces – AISC Manual 15 th Ed 99

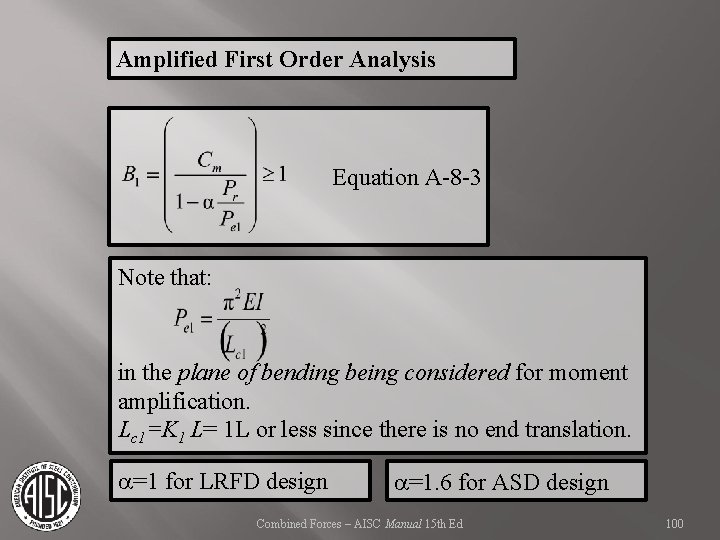
Amplified First Order Analysis Equation A-8 -3 Note that: in the plane of bending being considered for moment amplification. Lc 1=K 1 L= 1 L or less since there is no end translation. a=1 for LRFD design a=1. 6 for ASD design Combined Forces – AISC Manual 15 th Ed 100

Amplified First Order Analysis For cases where member has end moment only (no transverse loads applied): Cm = 0. 6 - 0. 4(M 1/M 2) Equation A-8 -4 M 1 = smaller first order end moment M 2 = larger first order end moment For cases where loads are present transverse to the member: y from Table C-A-8. 1 Combined Forces – AISC Manual 15 th Ed 101

Amplified First Order Analysis M 1 M 2=M 1 (largest possible value) M 1 (smallest possible value) M 2=-M 1 Combined Forces – AISC Manual 15 th Ed 102

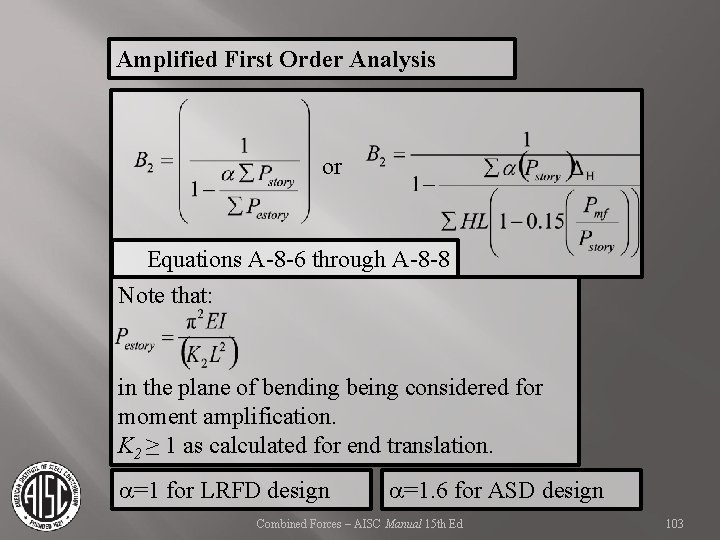
Amplified First Order Analysis or Equations A-8 -6 through A-8 -8 Note that: in the plane of bending being considered for moment amplification. K 2 ≥ 1 as calculated for end translation. a=1 for LRFD design a=1. 6 for ASD design Combined Forces – AISC Manual 15 th Ed 103

Amplified First Order Analysis Combined Forces – AISC Manual 15 th Ed 104

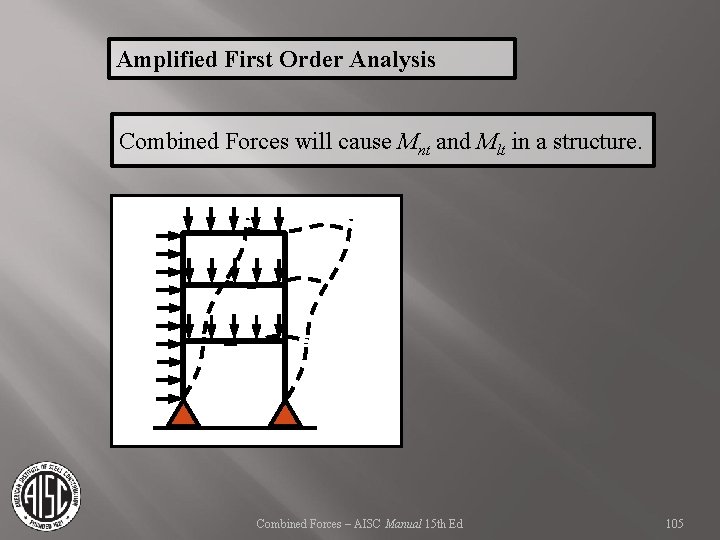
Amplified First Order Analysis Combined Forces will cause Mnt and Mlt in a structure. Combined Forces – AISC Manual 15 th Ed 105

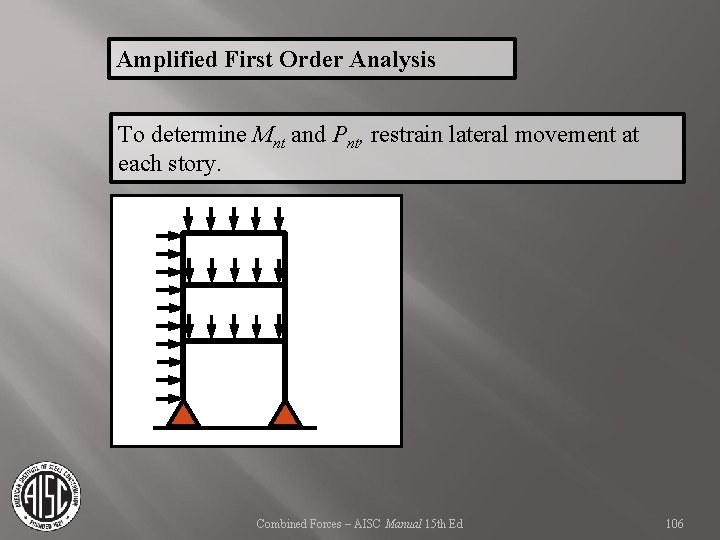
Amplified First Order Analysis To determine Mnt and Pnt, restrain lateral movement at each story. Combined Forces – AISC Manual 15 th Ed 106

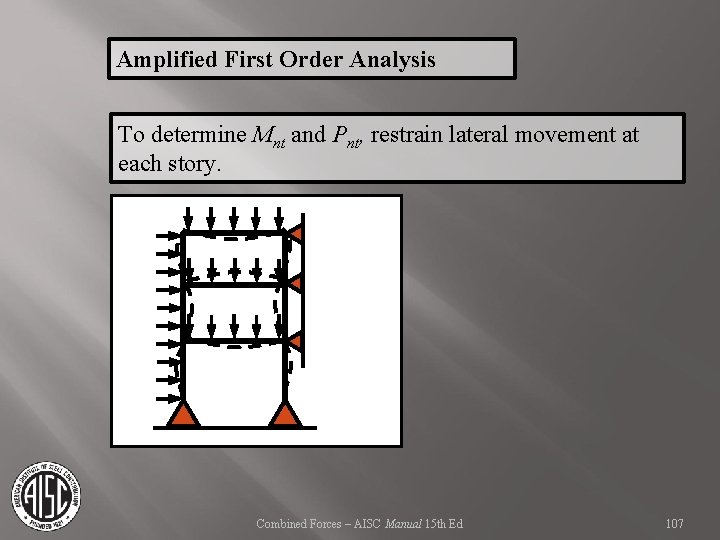
Amplified First Order Analysis To determine Mnt and Pnt, restrain lateral movement at each story. Combined Forces – AISC Manual 15 th Ed 107

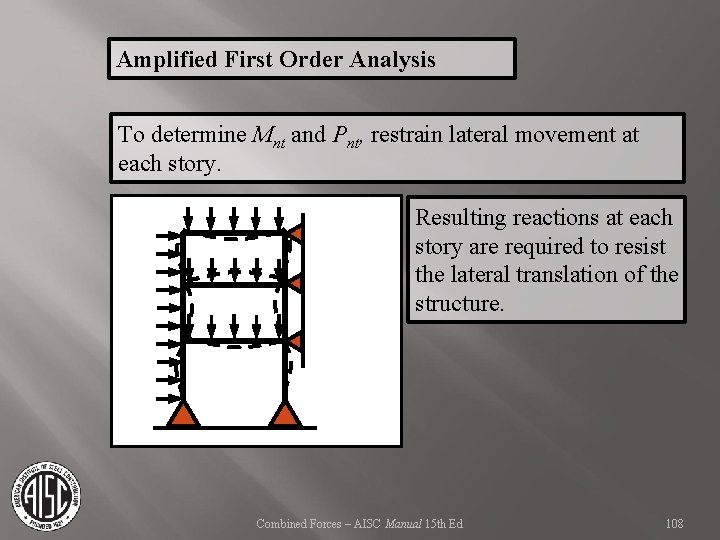
Amplified First Order Analysis To determine Mnt and Pnt, restrain lateral movement at each story. Resulting reactions at each story are required to resist the lateral translation of the structure. Combined Forces – AISC Manual 15 th Ed 108

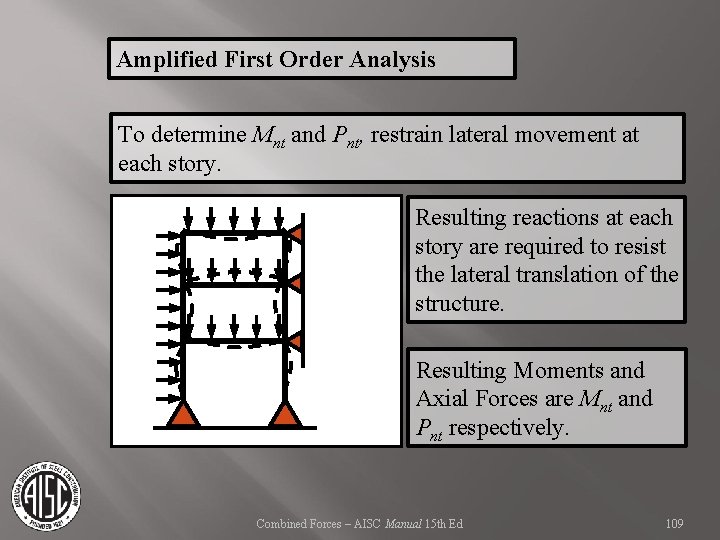
Amplified First Order Analysis To determine Mnt and Pnt, restrain lateral movement at each story. Resulting reactions at each story are required to resist the lateral translation of the structure. Resulting Moments and Axial Forces are Mnt and Pnt respectively. Combined Forces – AISC Manual 15 th Ed 109

Amplified First Order Analysis To determine Mlt and Plt, apply the resulting reaction at each story. Combined Forces – AISC Manual 15 th Ed 110

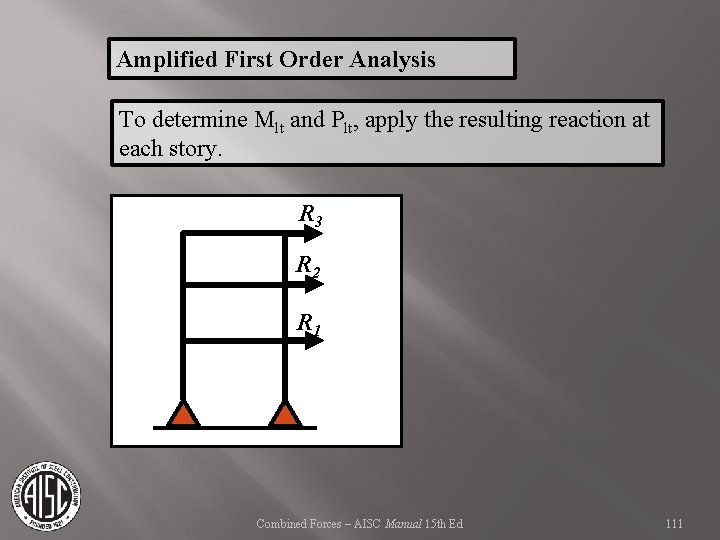
Amplified First Order Analysis To determine Mlt and Plt, apply the resulting reaction at each story. R 3 R 2 R 1 Combined Forces – AISC Manual 15 th Ed 111

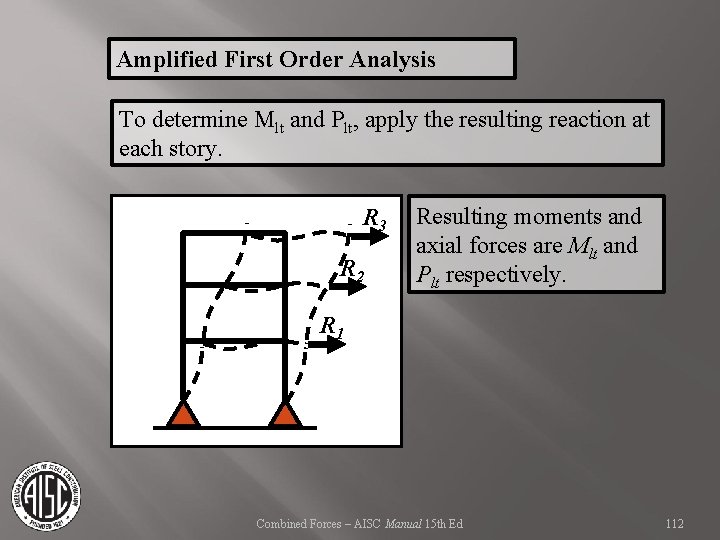
Amplified First Order Analysis To determine Mlt and Plt, apply the resulting reaction at each story. R 3 R 2 Resulting moments and axial forces are Mlt and Plt respectively. R 1 Combined Forces – AISC Manual 15 th Ed 112

DIRECT ANALYSIS METHOD COMPARISON TO TRADITIONAL (K FACTOR) METHOD Combined Forces Theory 113

DIRECT ANALYSIS METHOD Analysis of entire structure interaction. Additional lateral “Notional” loads. Reduced stiffness of structure. No K values required. Combined Forces Theory 114

DIRECT ANALYSIS METHOD Axial Force, P Initially consider a “traditional” analysis Moment, M Combined Forces Theory 115

DIRECT ANALYSIS METHOD Initially consider a “traditional” analysis Axial strength is defined as Pn. KL which includes K factors (Py indicates crushing). Axial Force, P Py Pn. KL Moment, M Combined Forces Theory 116

DIRECT ANALYSIS METHOD Initially consider a “traditional” analysis Axial strength is defined as Pn. KL which includes K factors (Py indicates crushing). Axial Force, P Py Pn. KL Bending Strength is defined as Mn, assumed here to be Mp for a laterally braced member. Moment, M Mp Combined Forces Theory 117

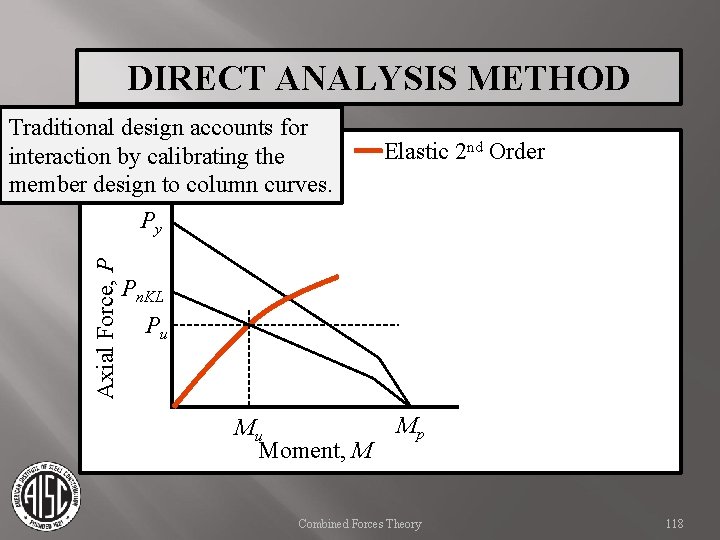
DIRECT ANALYSIS METHOD Axial Force, P Traditional design accounts for interaction by calibrating the member design to column curves. Py Elastic 2 nd Order Pn. KL Pu Mu Moment, M Mp Combined Forces Theory 118

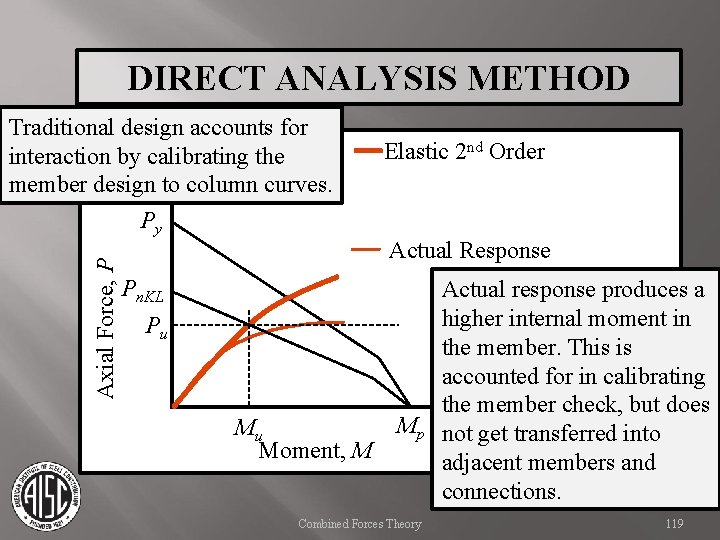
DIRECT ANALYSIS METHOD Axial Force, P Traditional design accounts for interaction by calibrating the member design to column curves. Py Elastic 2 nd Order Actual Response Pn. KL Pu Mu Moment, M Mp Combined Forces Theory Actual response produces a higher internal moment in the member. This is accounted for in calibrating the member check, but does not get transferred into adjacent members and connections. 119

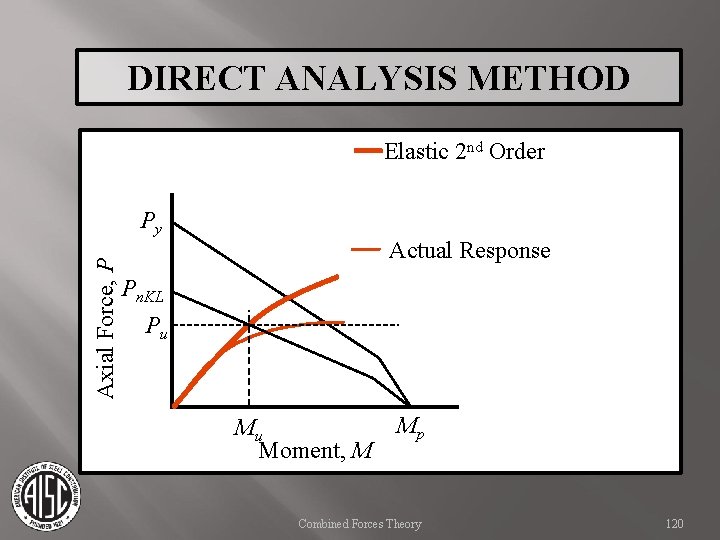
DIRECT ANALYSIS METHOD Elastic 2 nd Order Axial Force, P Py Actual Response Pn. KL Pu Mu Moment, M Mp Combined Forces Theory 120

DIRECT ANALYSIS METHOD Axial Force, P Now consider the “Direct” analysis Moment, M Combined Forces Theory 121

DIRECT ANALYSIS METHOD Axial Force, P Now consider the “Direct” analysis Axial strength is defined as Pn. L which assumes K=1 for all cases. Py Pn. L Moment, M Combined Forces Theory 122

DIRECT ANALYSIS METHOD Axial Force, P Now consider the “Direct” analysis Axial strength is defined as Pn. L which assumes K=1 for all cases. Py Pn. L Bending strength is defined as Mn, assumed here to be Mp for a laterally braced member. Moment, M Mp Combined Forces Theory 123

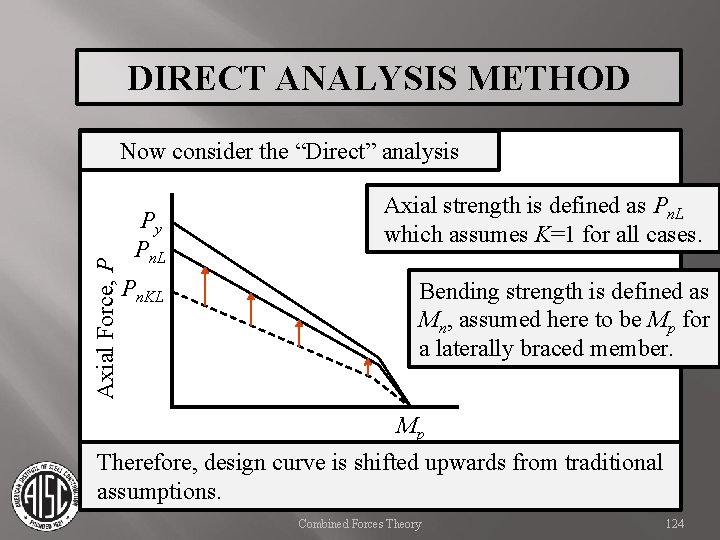
DIRECT ANALYSIS METHOD Axial Force, P Now consider the “Direct” analysis Py Pn. L Pn. KL Axial strength is defined as Pn. L which assumes K=1 for all cases. Bending strength is defined as Mn, assumed here to be Mp for a laterally braced member. Mp Moment, M Therefore, design curve is shifted upwards from traditional assumptions. Combined Forces Theory 124

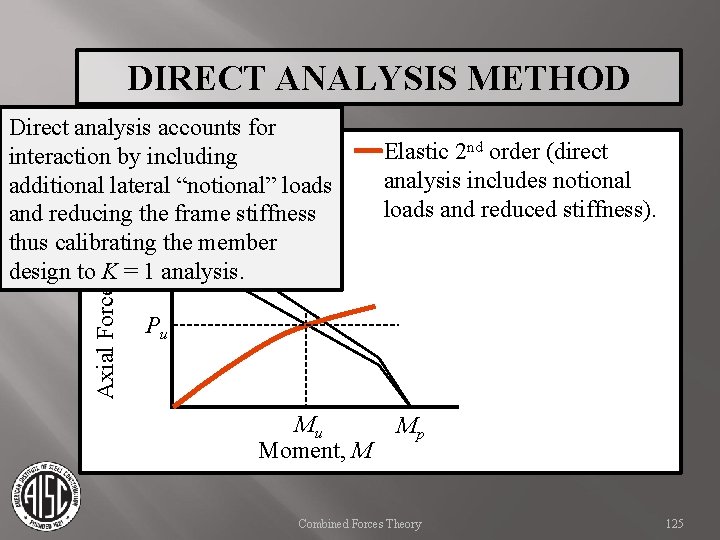
DIRECT ANALYSIS METHOD Axial Force, P Direct analysis accounts for interaction by including additional lateral “notional” loads and reducing the frame stiffness Py thus calibrating the member Pn. L design to K = 1 analysis. Elastic 2 nd order (direct analysis includes notional loads and reduced stiffness). Pu Mu Moment, M Mp Combined Forces Theory 125

DIRECT ANALYSIS METHOD Axial Force, P Direct analysis accounts for interaction by including additional lateral “notional” loads and reducing the frame stiffness Py thus calibrating the member Pn. L design to K = 1 analysis. Elastic 2 nd order (direct analysis includes notional loads and reduced stiffness). Actual Response Pu Mu Moment, M Mp Combined Forces Theory Actual response then should match the internal moment, transferring this moment into adjacent members and connections during analysis. 126

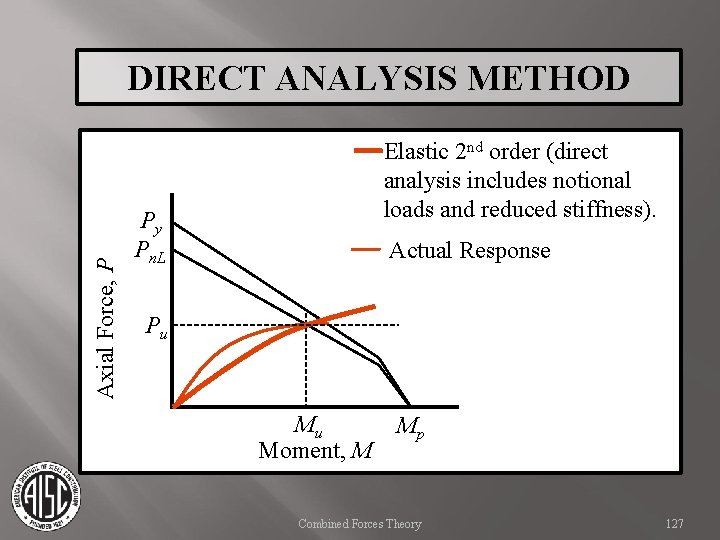
Axial Force, P DIRECT ANALYSIS METHOD Elastic 2 nd order (direct analysis includes notional loads and reduced stiffness). Py Pn. L Actual Response Pu Mu Moment, M Mp Combined Forces Theory 127

DIRECT ANALYSIS METHOD Direct Analysis and Traditional methods are valid for design. Each is reliant on calibration to match the response curves shown on previous slides. The Direct Analysis method has been calibrated for typical building structures. Unusual structures (such as a cantilever with compression and bending) may require additional calibration. Combined Forces Theory 128

DIRECT ANALYSIS METHOD Analysis and Calibration With proper calibration design strength approaches the actual response. Calibration consists of a combination of notional load values and reduction in member stiffness. Analysis is referenced to K = 1 member capacities. Combined Forces Theory 129