Teaching Modules for Steel Instruction Advanced Flexure Design

Teaching Modules for Steel Instruction Advanced Flexure Design COMPOSITE BEAM THEORY SLIDES Developed by Scott Civjan University of Massachusetts, Amherst Composite Beam Theory 1

Composite Beams Composite action accounts for the steel beam and floor slab working together to resist bending moments. Advantages over non-composite design: Increased strength Increased stiffness For given load conditions can achieve: Less steel required Reduced steel depth Composite Beam Theory 2

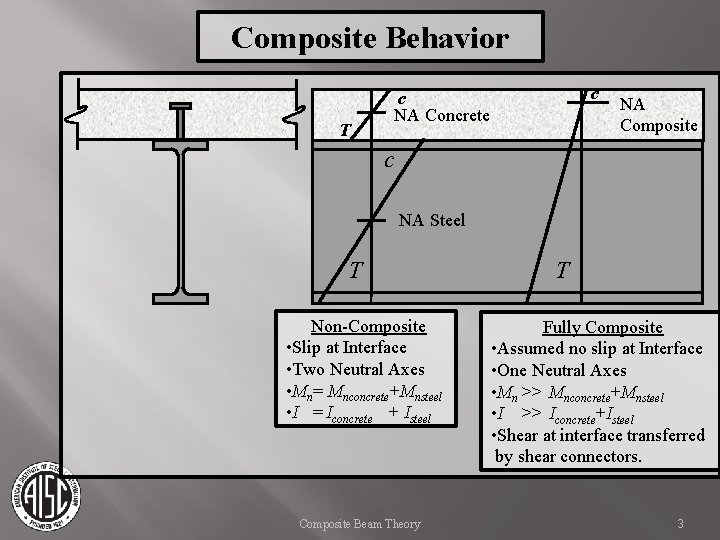
Composite Behavior T c c NA Concrete NA Composite c NA Steel T Non-Composite • Slip at Interface • Two Neutral Axes • Mn= Mnconcrete+Mnsteel • I = Iconcrete + Isteel Composite Beam Theory T Fully Composite • Assumed no slip at Interface • One Neutral Axes • Mn >> Mnconcrete+Mnsteel • I >> Iconcrete+Isteel • Shear at interface transferred by shear connectors. 3

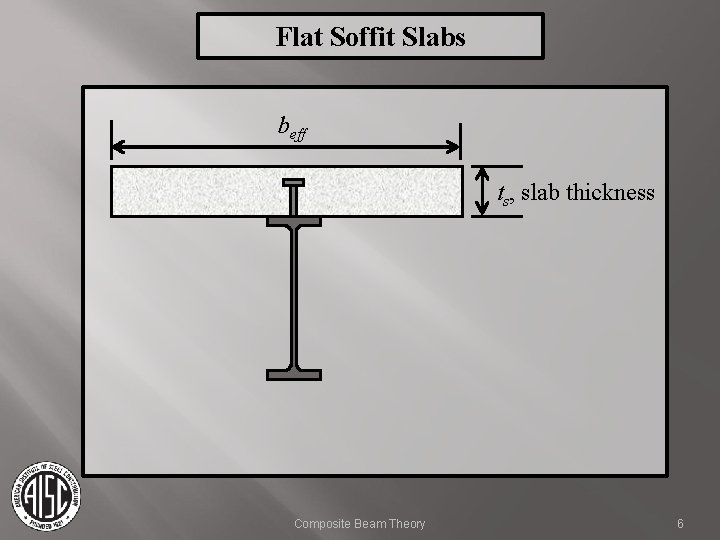
Slabs Composite Metal Deck Slabs – most commonly used today. Advantages: Stay in place form. Slab shoring typically not required. Metal deck serves as positive reinforcement. Metal deck serves as construction platform. Flat Soffit Slabs – typically, older construction. Composite Beam Theory 4

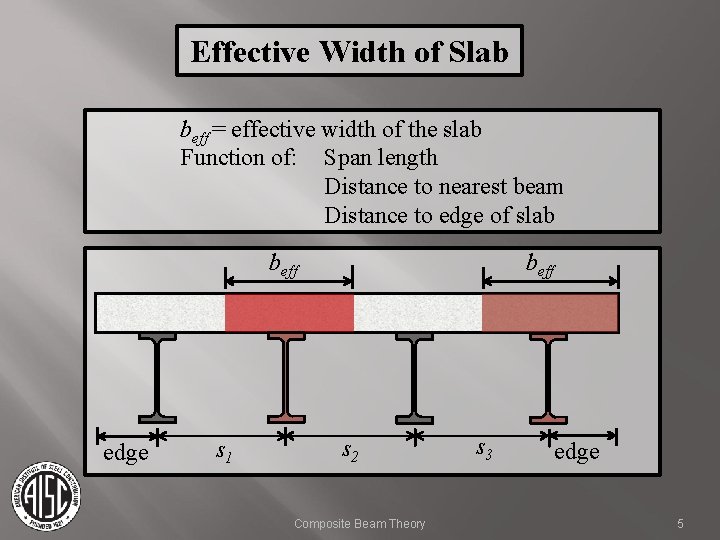
Effective Width of Slab beff = effective width of the slab Function of: Span length Distance to nearest beam Distance to edge of slab beff edge s 1 beff s 2 Composite Beam Theory s 3 edge 5

Flat Soffit Slabs beff ts, slab thickness Composite Beam Theory 6

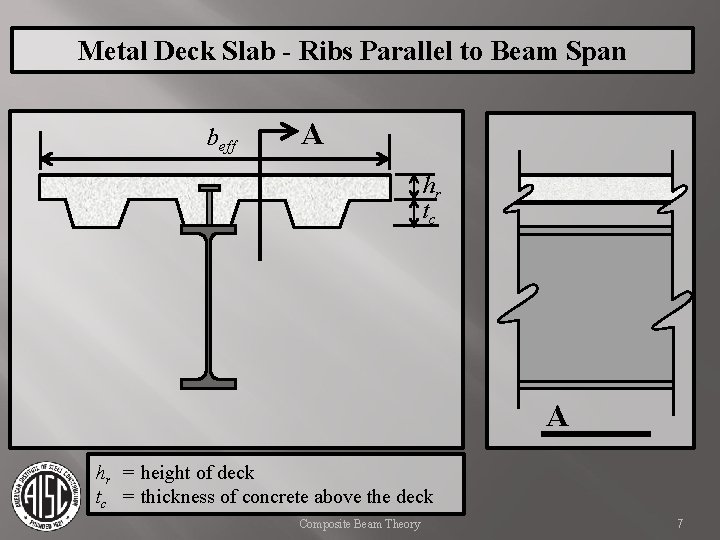
Metal Deck Slab - Ribs Parallel to Beam Span beff A hr tc A hr = height of deck tc = thickness of concrete above the deck Composite Beam Theory 7

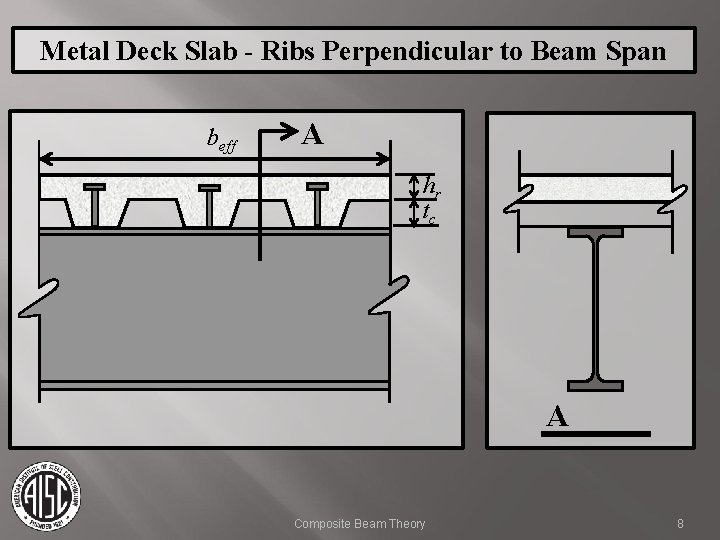
Metal Deck Slab - Ribs Perpendicular to Beam Span beff A hr tc A Composite Beam Theory 8

REFERENCES: COMPOSITE BEAMS Steel Deck Institute web pages Nelson Headed Studs web pages Steel Deck Manufacturer Catalogs These can be found on-line Composite Beam Theory 9

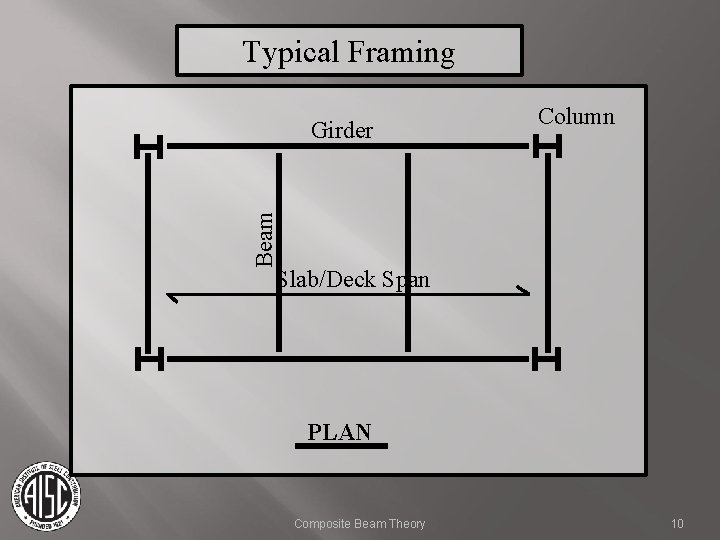
Typical Framing Column Beam Girder Slab/Deck Span PLAN Composite Beam Theory 10

INSERT PHOTOS: AISC Four Story Office Building Photo Slide Shows Metal Decking Slides Shear Studs Slides Composite Beam Theory 11

Flexural Strength Composite Beam Theory 12

Flexural Strength Positive Moment The strength is determined as the plastic stress distribution on the composite section. Negative Moment It typically is assumed that the concrete carries no tensile forces and reinforcement is minimal, therefore strength is identical to a bare steel section. Composite Beam Theory 13

Flexural Strength Positive Moment Fully Composite: The strength of either the floor slab in compression or the steel beam in tension is transferred at the interface. Partially Composite: The force transfer between the slab and beam is limited by the connectors. Composite Beam Theory 14

Flexural Strength Positive Moment Lateral Torsional Buckling is prevented by the slab (continuous bracing). Local Flange Buckling is minimized by the slab. In general, strength is controlled by Mp. Composite Beam Theory 15

INSERT INFORMATION: STRENGTH OF FULLY COMPOSITE BEAM SECTION CALCULATIONS Handout on Calculations: Fully. Composite. Calcs. PDF Composite Beam Theory 16

Flexural Strength The bare steel section must support the temporary construction loads (before the concrete has set), or the steel beam must be shored until the composite section is effective. Composite Beam Theory 17

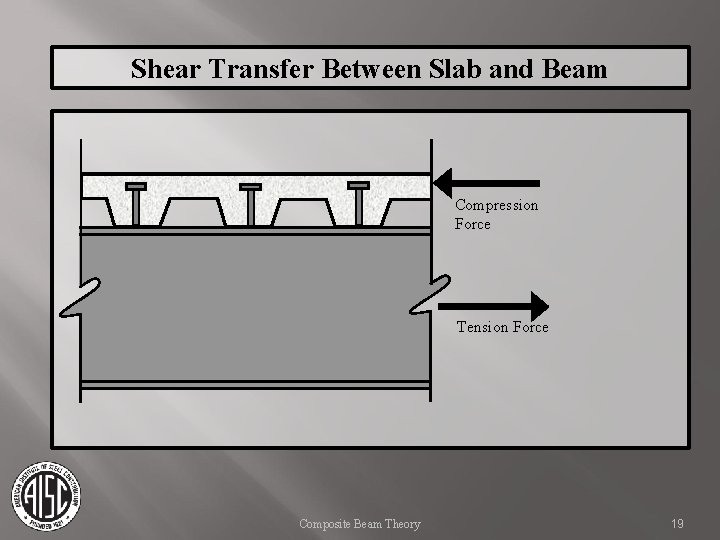
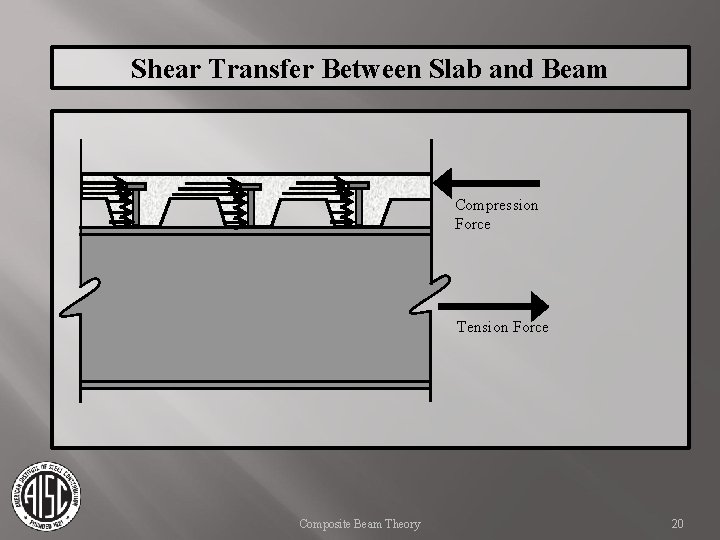
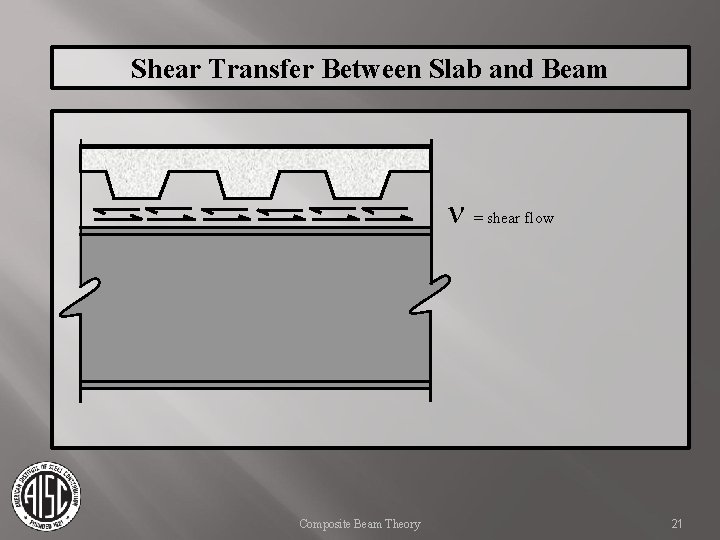
Shear Transfer Between Slab and Beam Typically, provided by headed shear studs. Shear flow, n, is calculated along the interface between slab and beam. Minimal slip allows redistribution of forces among shear studs. Therefore, studs are uniformly distributed along the beam. The total shear flow, n, must be provided on each side of Mmax. Composite Beam Theory 18

Shear Transfer Between Slab and Beam Compression Force Tension Force Composite Beam Theory 19

Shear Transfer Between Slab and Beam Compression Force Tension Force Composite Beam Theory 20

Shear Transfer Between Slab and Beam n = shear flow Composite Beam Theory 21

Shear Transfer Between Slab and Beam n= V= Q= Itr = shear flow to be transferred by shear studs Shear at the location considered first moment of inertia of area above the interface moment of inertia of the transformed cross section Composite Beam Theory 22

Partially Composite Beam Consider when fully composite strength is greater than required. This may occur when: The shape is based on construction loads. The shape is based on architectural constraints. The lightest shape has excess strength. Composite Beam Theory 23

INSERT INFORMATION: STRENGTH OF PARTIALLY COMPOSITE BEAM SECTION CALCULATIONS Handout on Calculations: Partially. Composite. Calcs. PDF Composite Beam Theory 24

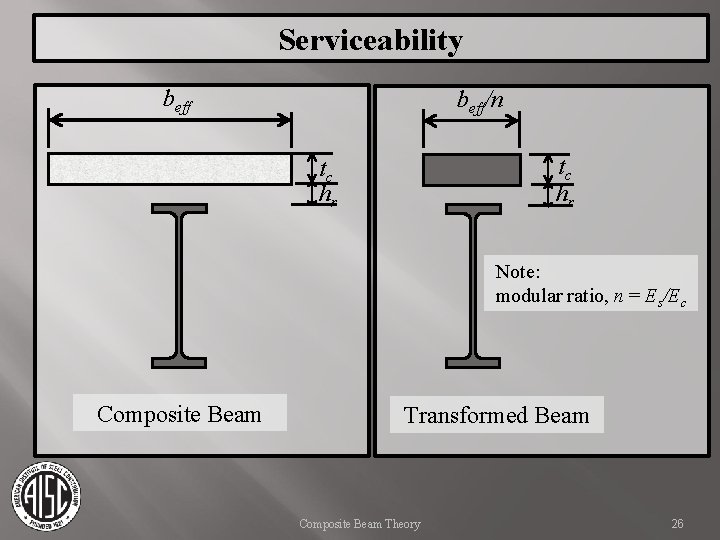
Serviceability For composite section deflections: Transform section into equivalent steel section. Compute center of gravity of transformed section. Compute Itr of transformed section. Composite Beam Theory 25

Serviceability beff/n tc hr Note: modular ratio, n = Es/Ec Composite Beam Transformed Beam Composite Beam Theory 26

Shear Strength It typically is assumed that the slab carries no shear forces, therefore composite strength is identical to that of a bare steel section. Composite Beam Theory 27

Teaching Modules for Steel Instruction Advanced Beam Design COMPOSITE BEAM th AISC Manual -14 Edition Developed by Scott Civjan University of Massachusetts, Amherst 28

Chapter I: Composite Member Design Composite Beam - AISC Manual 14 th Ed 29

Slab effective width, be To each side of the beam, be is limited by: one-eighth beam span one-half distance to adjacent beam distance to edge of slab Lowest value controls. Composite Beam - AISC Manual 14 th Ed 30

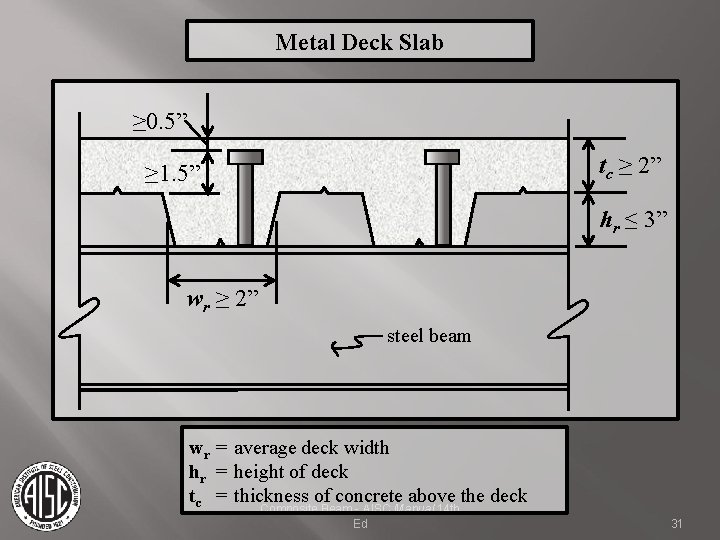
Metal Deck Slab ≥ 0. 5” tc ≥ 2” ≥ 1. 5” hr ≤ 3” wr ≥ 2” steel beam wr = average deck width hr = height of deck tc = thickness of concrete above the deck Composite Beam - AISC Manual 14 th Ed 31

Fully Composite Beam: Bending Strength Composite Beam - AISC Manual 14 th Ed 32

Bending Strength fb = 0. 90 (Wb = 1. 67) Composite Beam - AISC Manual 14 th Ed 33

Bending Strength POSITIVE MOMENT For h/tw The strength is determined as the plastic stress distribution of the composite section. (*Note: All current ASTM A 6 W, S and HP shapes satisfy this limit. ) NEGATIVE MOMENT It is typically assumed that the concrete carries no tensile forces and reinforcement is minimal, therefore strength is identical to a bare steel section. Composite Beam - AISC Manual 14 th Ed 34

INSERT INFORMATION: STRENGTH OF FULLY COMPOSITE BEAM SECTION CALCULATIONS Handout on Calculations: Fully. Composite. Calcs. PDF Composite Beam - AISC Manual 14 th Ed 35

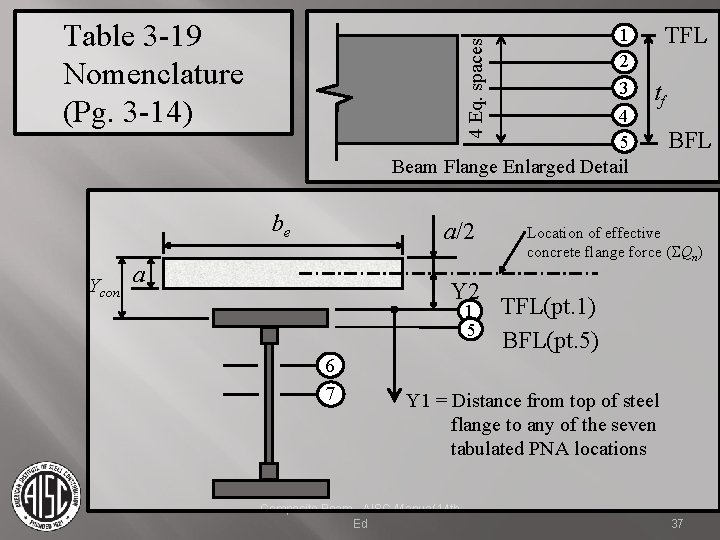
Bending Strength Fully Composite Strength can be determined by using Table 3 -19. Y 2 - Calculated per handout Y 1 = 0 if PNA in the slab, Calculated per handout if PNA in the beam flange or web. Composite Beam - AISC Manual 14 th Ed 36

1 2 3 4 Eq. spaces Table 3 -19 Nomenclature (Pg. 3 -14) 4 5 TFL tf BFL Beam Flange Enlarged Detail be Ycon a/2 a Y 2 1 5 6 7 Location of effective concrete flange force (SQn) TFL(pt. 1) BFL(pt. 5) Y 1 = Distance from top of steel flange to any of the seven tabulated PNA locations Composite Beam - AISC Manual 14 th Ed 37

Bending Strength To reach fully composite strength, shear studs must transfer SQn for Y 1 = 0 (maximum value) listed in Table 3 -19. This is equivalent to value C* in calculations (handout). Composite Beam - AISC Manual 14 th Ed 38

Shear Stud Strength Composite Beam - AISC Manual 14 th Ed 39

Strength of each stud, Qn Equation I 8 -1 limits value to crushing of concrete around the shear stud. limits value to strength of individual shear studs. Composite Beam - AISC Manual 14 th Ed 40

Asa = cross sectional area of shear stud Ec = modulus of elasticity of concrete Fu = shear stud minimum tensile strength (typically 65 ksi) Rg accounts for number of studs welded in each deck rib and wr/hr. Values are 1. 0, 0. 85 or 0. 7. Rp accounts for deck rib orientation with respect to the beam, stud engagement in the concrete above the rib, and weak or strong stud location. Values are 0. 75 or 0. 6. Composite Beam - AISC Manual 14 th Ed 41

Strength, Qn, for one shear stud Table 3 -21 Composite Beam - AISC Manual 14 th Ed 42

Limitations on shear stud placement for shear studs placed in metal decking: Center-Center Spacing: > 4 times diameter ≤ 8 times slab thickness ≤ 36 inches Shear Stud Diameter: ≤ 3/4” ≤ 2. 5 times flange thickness unless over web Composite Beam - AISC Manual 14 th Ed 43

Composite strength requires that shear studs transfer SQn to each side of the maximum moment in the span. If SQn strength of the shear studs is inadequate to provide fully composite action, the beam is partially composite. Composite Beam - AISC Manual 14 th Ed 44

Partially Composite Beam: Bending Strength Fb = 0. 90 (Wb = 1. 67) Composite Beam - AISC Manual 14 th Ed 45

INSERT INFORMATION: STRENGTH OF PARTIALLY COMPOSITE BEAM SECTION CALCULATIONS Handout on Calculations: Partially. Composite. Calcs. PDF Composite Beam - AISC Manual 14 th Ed 46

Partially Composite Strength can be determined by using Table 3 -19. Y 2 - Calculated per handout Y 1 - Calculated per handout Composite Beam - AISC Manual 14 th Ed 47

Partially Composite Action is limited by the total strength of shear studs. SQn listed in Table 3 -19. This is equivalent to value C* in calculations (handout). Composite Beam - AISC Manual 14 th Ed 48

Composite Beam: Shear Strength Composite Beam - AISC Manual 14 th Ed 49

SHEAR STRENGTH It typically is assumed that the slab carries no shear forces. Therefore, strength is identical to a bare steel section. Composite Beam - AISC Manual 14 th Ed 50

Composite Beam Deflection Calculations Composite Beam - AISC Manual 14 th Ed 51

Deflection Calculations Fully Composite Itr = transformed section moment of inertia Lower bound values of Itr are found in Table 3 -20. Values assume concrete area equal to SQn/Fy rather than actual area. Composite Beam - AISC Manual 14 th Ed 52

Deflection Calculations Partially Composite Equation C-I 3 -4 Ieff = Is = Itr = ΣQnr= Cf = effective moment of inertia of steel section only fully composite moment of inertia partially composite shear transfer fully composite shear transfer Composite Beam - AISC Manual 14 th Ed 53

Deflection Calculations Partially Composite Equation C-I 3 -5 Seff = Ss = Str = ΣQnr= Cf = effective elastic section modulus of steel section only fully composite elastic section modulus partially composite shear transfer fully composite shear transfer Composite Beam - AISC Manual 14 th Ed 54

Deflection Calculations Partially Composite Table 3 -20 can be used for lower bound values of Ieff. Composite Beam - AISC Manual 14 th Ed 55