Teaching Dimension and the Complexity of Active Learning

Teaching Dimension and the Complexity of Active Learning Steve Hanneke Machine Learning Department Carnegie Mellon University shanneke@cs. cmu. edu

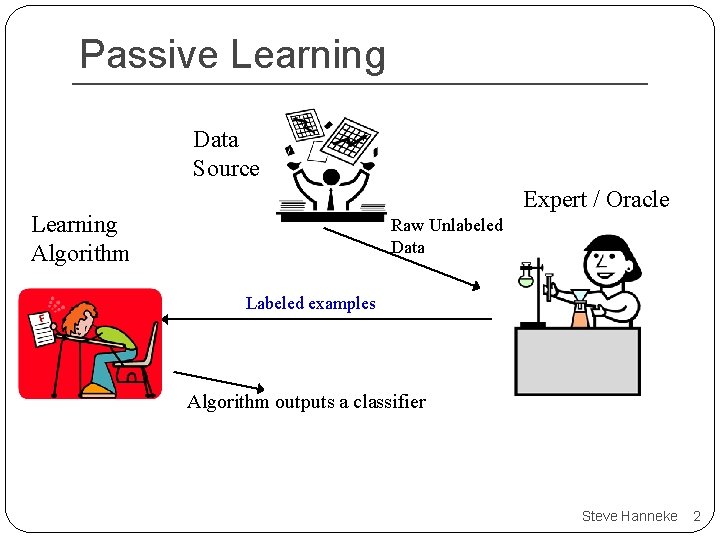
Passive Learning Data Source Expert / Oracle Learning Algorithm Raw Unlabeled Data Labeled examples Algorithm outputs a classifier Steve Hanneke 2

Active Learning Algorithm Data Source Expert / Oracle Raw Unlabeled Data How many label requests are needed to learn? Label Complexity Request for the label of an example The label of that example Request for the label of another example The label of that example. . . Algorithm outputs a classifier Steve Hanneke 3

Outline Formal Model Extended Teaching Dimension Generalization to statistical learning Main Result: Upper Bound on the Label Complexity Steve Hanneke 4

Formal Model Steve Hanneke 5

History Exact Learning Extended Teaching Dimension (XTD(C)): [Hegedüs, 95] Number of membership queries to build an equivalence Halving Algorithm XTD(C) log |C| membership queries query. suffice. Such an R is called a “specifying set for f w. r. t. C” Unavoidable (due to lower bound) [Kääriäinen, 06] Steve Hanneke 6

An Example: Discrete Thresholds Suppose C is thresholds on these points. - - -+ -+ -+ + + + + Steve Hanneke 7

An Example: Discrete Thresholds Suppose C is thresholds on these points. - -+ -+ + + -+ -+ -+ For each f, find a smallest set of examples s. t. there is at most one concept in C that agrees with f on them. (i. e. , a minimal specifying set) So, for discrete thresholds, XTD(C) = 2. Steve Hanneke 8

Extended Teaching Dimension What about PAC-style active learning? Let’s look at Thresholds on [0, 1]. 0 - + 1 XTD(C) = ∞ This doesn’t make sense anymore, but can we generalize it? Steve Hanneke 9

Extended Teaching Dimension What about PAC-style active learning? Let’s look at Thresholds on [0, 1]. 0 1 Let’s use XTD for a finite sample U. Now XTD(C, U)=2 again. Steve Hanneke 10

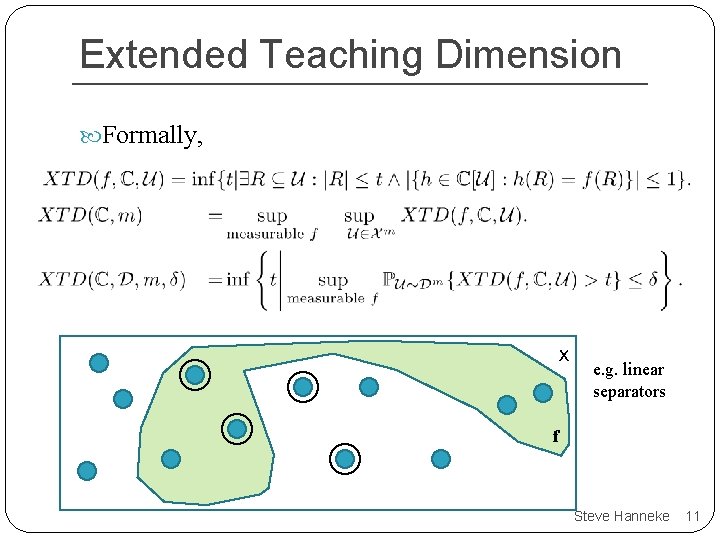
Extended Teaching Dimension Formally, X e. g. linear separators f Steve Hanneke 11

Obvious Bound (Realizable) Formally, “Obvious” bound: Steve Hanneke 12

Distribution-Dependent (Realizable) Suppose the target is f. hmaj Steve Hanneke 13

What About Noisy Labels? Two stage algorithm: “Reduction” and “Error Correction” Reduction: Halving-like. Focus on hmaj. Reduce size of version space by constant factor on each iteration. - produces a concept with a “decent” error rate. Error Correction: Given a “decent” concept, use it to label a large unlabeled data set, but with some tricks to correct mistakes. Steve Hanneke 14

What About Noisy Labels? Stage 1 Steve Hanneke 15

Open Problem Conjecture: The bound holds for Agnostic Learning, (up to constant factors). Steve Hanneke 16

Thank You Steve Hanneke 17

Shameless Plug Hanneke, S. (2007). A Bound on the Label Complexity of Agnostic Active Learning. ICML 2007. Disagreement Coefficient – Sometimes not as tight as XTD, but much simpler to calculate and comprehend, and applies directly to agnostic learning. Steve Hanneke 18

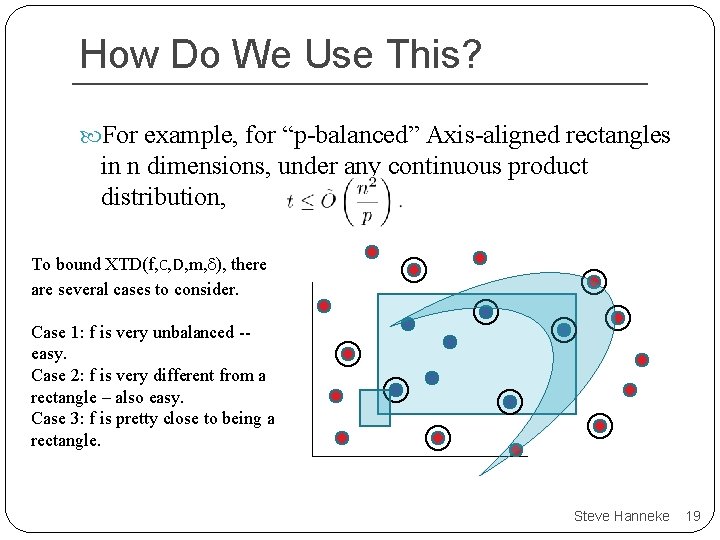
How Do We Use This? For example, for “p-balanced” Axis-aligned rectangles in n dimensions, under any continuous product distribution, To bound XTD(f, C, D, m, ), there are several cases to consider. Case 1: f is very unbalanced -easy. Case 2: f is very different from a rectangle – also easy. Case 3: f is pretty close to being a rectangle. Steve Hanneke 19