Teaching Computing to GCSE Level with Python Sue

Teaching Computing… …to GCSE Level with Python Sue Sentance Sue. sentance@anglia. ac. uk

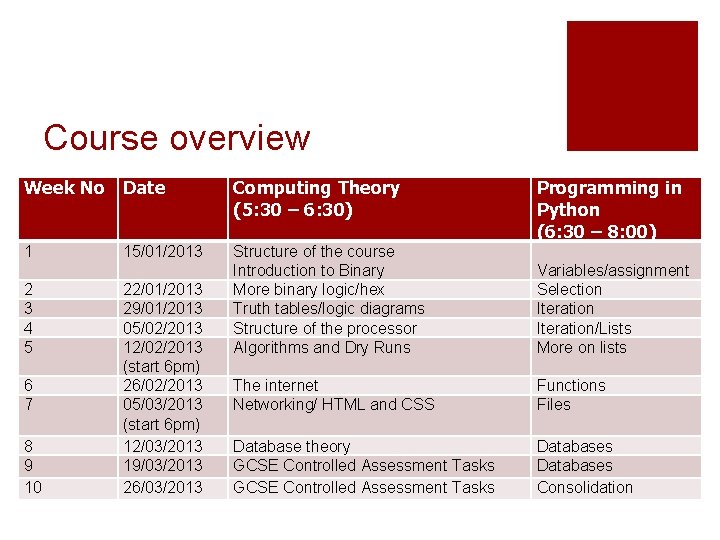
Course overview Week No Date Computing Theory (5: 30 – 6: 30) Programming in Python (6: 30 – 8: 00) 1 15/01/2013 2 3 4 5 22/01/2013 29/01/2013 05/02/2013 12/02/2013 (start 6 pm) 26/02/2013 05/03/2013 (start 6 pm) 12/03/2013 19/03/2013 26/03/2013 Structure of the course Introduction to Binary More binary logic/hex Truth tables/logic diagrams Structure of the processor Algorithms and Dry Runs Variables/assignment Selection Iteration/Lists More on lists The internet Networking/ HTML and CSS Functions Files Database theory GCSE Controlled Assessment Tasks Databases Consolidation 6 7 8 9 10

Available specifications for 20122013 ¡OCR – will be in third year ¡Ed. Excel – now delayed until September 2013 ¡AQA – up and running from September 2012 ¡Behind the Screen – E-Skills work-in-progress to create a GCSE in Computer Science

OCR GCSE Computing 3 units A 451 – Theory (Examination) A 452 – Practical investigation (Controlled Assessment) A 453 – Programming (Controlled Assignment)

AQA Computer Science ¡Component 1 – Practical programming 50 hours controlled assessment Worth 60% ¡Component 2 – Computing fundamentals 1 ½ hour examination Worth 40%

Today’s session 4: 45 – 5: 45 Binary & Binary arithmetic/ Hex 6. 00 – 7. 30 Starting to program in Python

From the specification OCR AQA ¡ (a) define the terms bit, nibble, byte, kilobyte, megabyte, gigabyte, terabyte ¡ understand that computers use the binary alphabet to represent all data and instructions ¡ (b) understand that data needs to be converted into a binary format to be pro ¡ understand the terms bit, nibble, byte, kilobyte, megabyte gigabyte and terabyte ¡ (c) convert positive denary whole numbers (0 -255) into 8 -bit binary numbers and vice versa ¡ understand that a binary code could represent different types of data such as text, image, sound, integer, date, real number ¡ (d) add two 8 -bit binary integers and explain overflow errors which may occur ¡ (e) convert positive denary whole numbers (0 -255) into 2 digit hexadecim ¡ understand how binary can be used to represent positive whole numbers (up to 255) ¡ understand how sound and bitmap images can be represented in binary ¡ understand how characters are represented in binary and be familiar with ASCII and its limitations ¡ understand why hexadecimal number representation is often used and know how to convert between binary, denary and hexadecimal

Binary numbers 0

Binary numbers 1

Learning binary numbers ¡Converting binary to denary ¡Converting denary to binary ¡Binary addition

Storing Binary Numbers Inside the computer each binary digit is stored in a unit called a bit. A series of 8 bits is called a byte. A bit can take the values 0 and 1

What is meant by? 1 byte ? 1 nibble ? 1 kilobyte ? 1 megabyte ? 1 gigabyte ? 1 terabyte ?

Storing data 1 byte = 8 bits 1 nibble = 4 bits 1 kilobyte = 1024 bytes = 2 10 bytes 1 megabyte = 2 20 bytes = 210 kilobytes 1 gigabyte = 2 30 bytes = 210 megabytes 1 terabyte = 2 40 bytes = 2 10 gigabytes

Activity Binary counting exercise

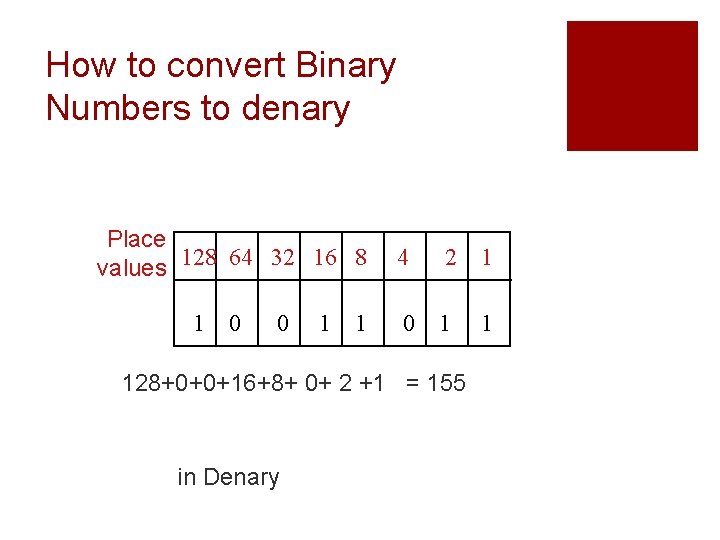
How to convert Binary Numbers to denary Place values 128 64 32 16 8 1 0 0 1 1 4 2 1 0 1 1 128+0+0+16+8+ 0+ 2 +1 = 155 in Denary

Storing Numbers - Binary EXAMPLE Convert the binary number 1011 0111 into denary: Answer 128 64 32 16 8 4 2 1 0 1 1 =128+32+16+4+2+1=183 1 1

Conversion Exercise Convert the following binary numbers into denary: 001 010 1001 101 110 1010 1111 1100 10101 10111 11111

Teaching binary ¡Holding cards up activity ¡Finger binary ¡Cisco binary game ¡CS Unplugged actitivies

Converting Denary to Binary ¡Write down the column headings for the binary number: 64 32 16 8 4 2 1 ¡Process each column from left to right. ¡If the denary number to be translated is greater than or equal to the column heading, place a 1 in the column and subtract the value of the column from the denary value. ¡If the denary value is smaller than the column heading, place a 0 in the column.

Convert to Binary 3 5 8 7 11 16 32 21 14 17 48 255

Sizes of Binary Numbers ¡If we have 4 bits available the largest number is 1 1 (which is 15 in denary) ¡If we have 5 bits available the largest number is 1 1 1 (denary value 31) ¡If we have 7 bits available the largest number is 1 1 1 1 (denary value 127) ¡If we have 8 bits available the largest number is 1 1 1 1 (denary value 255) ¡Can you see a pattern? animated

To calculate the max size ¡In general if we have n bits available then the largest denary number we can store is n 2 -1 ¡For example, for 3 bits, 1112 = 23 – 1 = 8 – 1 = 7

Addition Rules for Binary 0 + 0 = 0 1 + 0 = 1 0 + 1 = 1 1 + 1 = 10 (write down 0 and carry 1) 1 + 1 = 11 (write down 1 and carry 1)

Adding Binary Numbers add 8 and 5 8 1 0 0 0 5 0 1 --------13 1101 check the answer using place values: 8+4+0+1 = 13

Adding Binary Numbers add 9 and 5 9 1 0 0 1 5 0 1 1 --------14 1110 carry check the answer using place values: 8+4+2+0 = 14

Exercises – see sheet