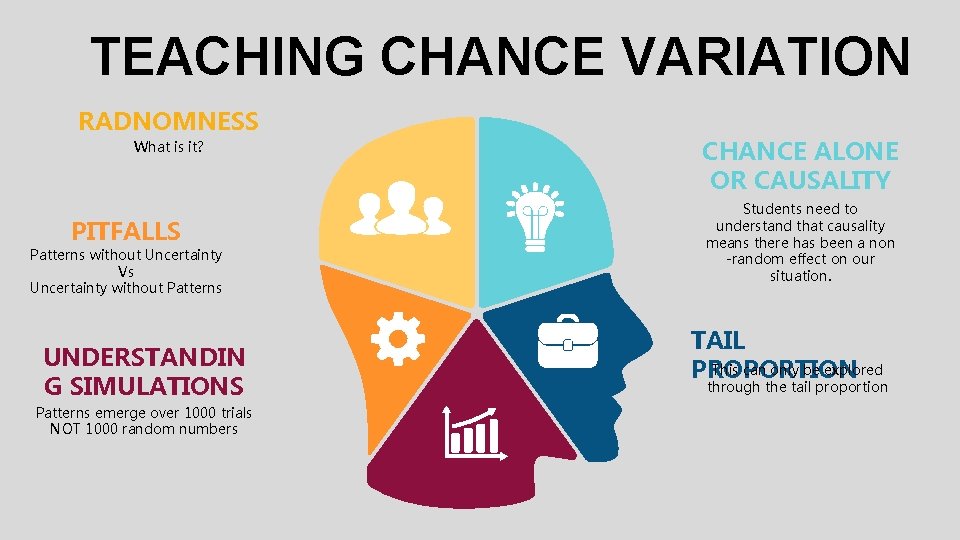
TEACHING CHANCE VARIATION RADNOMNESS What is it PITFALLS

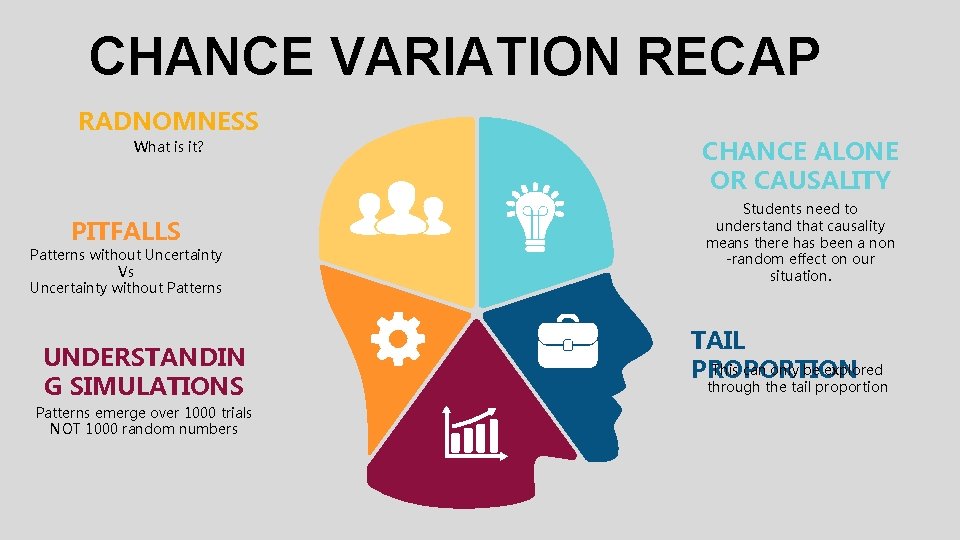
TEACHING CHANCE VARIATION RADNOMNESS What is it? PITFALLS Patterns without Uncertainty Vs Uncertainty without Patterns UNDERSTANDIN G SIMULATIONS Patterns emerge over 1000 trials NOT 1000 random numbers CHANCE ALONE OR CAUSALITY Students need to understand that causality means there has been a non -random effect on our situation. TAIL This can only be explored PROPORTION through the tail proportion

RANDOMNESS Events that have uncertain individual outcomes but a regular pattern of outcomes in many repetitions are called random.

Success Criteria: (1) I can specify the two facets of an event that make it random Events that have uncertain individual outcomes but a regular pattern of outcomes in many repetitions are called random. TASK: Think-Pair-Share: 1. Susan needs a total 4 when she rolls two dice and adds them to win the game. Describe fully what makes her next turn a random event 2. Ms Chida hands Emily a bag of lollies. In the bag, some lollies are red and some green. She knows everyone chooses the red lollies, and to make things fair she has students walk up, thrust their hand inside and choose their lolly without looking. Describe fully what makes this a random event 3. Anzar is on wheel of fortune and is about to spin the wheel. He has 3 spins, and he really hopes one of those spins lands on the “win a car” section. Describe fully what makes his spin a random event.

Success Criteria: (1) I understand that over repeated trials a pattern emerges (2) I can plan a trial using a sequence of random numbers (3) I can run a simple simulation PROBLEM Events that have uncertain individual outcomes but a regular pattern of outcomes in many repetitions are called random. Mr Chida has 3 daughters. He wonders how likely this is, what is the probability of having 3 children and they are all girls? The first thing we’ll need is work out the probability of having a girl. How could we do that? Probability worldwide (Experimental) Could take the last 50 generations in my family tree and find the prob of a girl being born (Experimental) Probability in New Zealand (Experimental) Could assume both outcomes equally likely (Theoretical)

Success Criteria: (1) I understand that over repeated trials a pattern emerges (2) I can plan a trial using a sequence of random numbers (3) I can run a simple simulation Events that have uncertain individual outcomes but a regular pattern of outcomes in many repetitions are called random. G G But today we are going to focus on working out this probability using SIMULATIONS B B G B G B

Success Criteria: (1) I understand that over repeated trials a pattern emerges (2) I can plan a trial using a sequence of random numbers (3) I can run a simple simulation PROBLEM Events that have uncertain individual outcomes but a regular pattern of outcomes in many repetitions are called random. Mr Chida has 3 daughters. He wonders how likely this is, what is the probability of having 3 children and they are all girls? Assume P(Girl)=0. 5 It is impossible to predict whether or not, when I have 3 children, all 3 will be girls. But if I had 3 children 50 times, and kept count of how many times all 3 were girls, I could work out a probability. Doing that literally is pretty laughable, but we can however SIMULATE having 3 children, 50 times

Success Criteria: (1) I understand that over repeated trials a pattern emerges (2) I can plan a trial using a sequence of random numbers (3) I can run a simple simulation PROBLEM Events that have uncertain individual outcomes but a regular pattern of outcomes in many repetitions are called random. Mr Chida has 3 daughters. He wonders how likely this is, what is the probability of having 3 children and they are all girls? Assume P(Girl)=0. 5 THINK PAIR SHARE: How could we simulate the birth of a single child using either a die or a coin? Set about running your simulation in groups Make sure you draw a table that will allow you to record every trial and its outcome. Run 50 simulations so that, at the end of it, you can estimate the probability of having 3 children and they all are girls

Running the same simulation on excel important video: https: //youtu. be/Y 7 x. Cpl 2 RAz. I

DAY 2

Key Points Although a reasonable prediction is unattainable for individual random events, at least prediction becomes possible over the long haul. ie. when the event is repeated many times Learning Objective For Today I understand that variations in estimates can be due either to chance alone or chance along with some form of underlying causality. From Gal, I. & Garfield, J. B. (editors). The Assessment Challenge in Statistics Education. IOS Press, 1997 (on behalf of the ISI). Pages 223 -238. ISBN 90 5199 333 1. Copyright holder: International Statistical Institute. Permission granted by ISI to the IASE to make the chapters from this book freely available on the Internet. The References section is a separate chapter and is available on the Internet at http: //www. stat. auckland. ac. nz/~iase/publications/assessbkref.

Learning Objective For Today I understand that variations in estimates can be due either to chance alone or chance alone with some form of underlying causality. •

Learning Objective For Today I understand that variations in estimates can be due either to chance alone or chance along with some form of underlying causality. No…. because of CHANCE ALONE, you would expect a different number to come up, like 4 yellows, you wouldn’t be surprised at all, because intuitively you would expect CHANCE ALL BY ITSELF to give you that variation from the expected 3 yellows to the 4 yellows when we did a trial BUT, though chance alone (chance all by itself) could easily make the number of yellows 4 instead of the estimated 3, it will have a harder time making it 9 yellows, and there is almost certainly ‘something up’, some sort of ‘causality’ involved, if our spinner gets to 12 yellows CAUSALITY: In this context, establishing causality is establishing that what you see is due to a non-random effect, ie. Something real has interfered with the supposedly random event The statistician needs a way of working out if the number of yellows seen is just due to CHANCE ALONE, or, some sort of CAUSALITY is involved as well, such as bias in the weighting of the spinner causing what we have seen in a particular trial

Learning Objective For Today I understand that variations in estimates can be due either to chance alone or chance along with some form of underlying causality. Plan a simulation as a class to study how many yellows you would get from 12 spins What differences do you find between this study and the one we did to explore having 3 girls

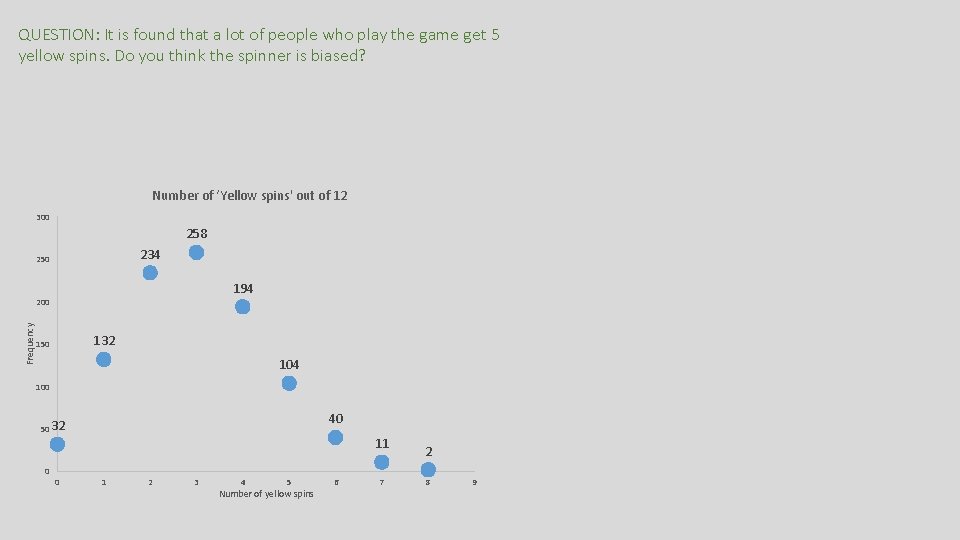
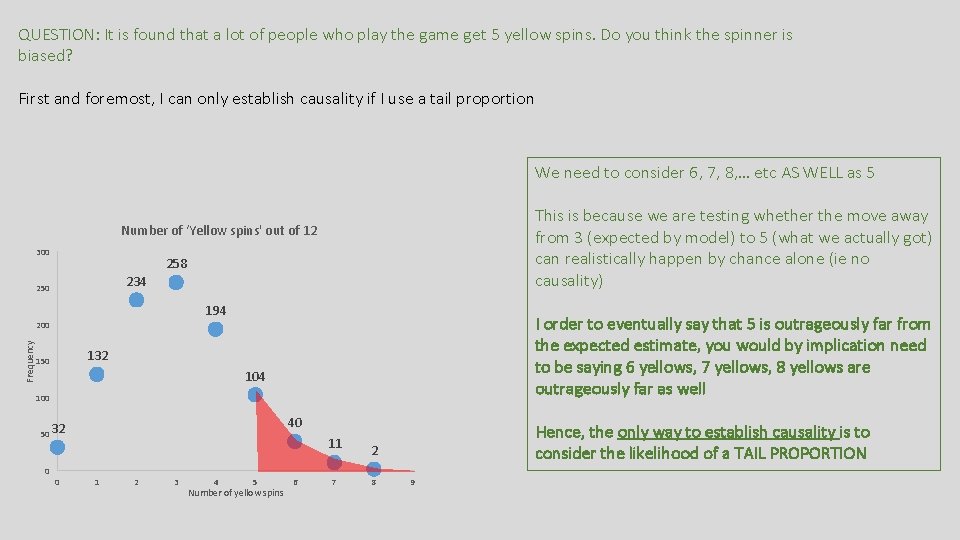
QUESTION: It is found that a lot of people who play the game get 5 yellow spins. Do you think the spinner is biased? Number of ‘Yellow spins' out of 12 300 258 234 250 194 Frequency 200 132 150 104 100 40 50 32 11 0 0 1 2 3 4 5 Number of yellow spins 6 7 2 8 9

QUESTION: It is found that a lot of people who play the game get 5 yellow spins. Do you think the spinner is biased? First and foremost, I can only establish causality if I use a tail proportion We need to consider 6, 7, 8, … etc AS WELL as 5 This is because we are testing whether the move away from 3 (expected by model) to 5 (what we actually got) can realistically happen by chance alone (ie no causality) Number of ‘Yellow spins' out of 12 300 258 234 250 194 I order to eventually say that 5 is outrageously far from the expected estimate, you would by implication need to be saying 6 yellows, 7 yellows, 8 yellows are outrageously far as well Frequency 200 132 150 104 100 40 50 32 0 0 11 1 2 3 4 5 Number of yellow spins 6 7 Hence, the only way to establish causality is to consider the likelihood of a TAIL PROPORTION 2 8 9

[tail proportion quoted] [tail propiortion in context] [Is that above/below 5%] [therefore it is possible chance alone caused this/therefore it is unlikely that chance alone caused this] [Make a call or do not make a call establishing causality] Number of ‘Yellow spins' out of 12 300 258 234 250 194 Frequency 200 132 150 104 100 40 50 32 0 0 11 1 2 3 4 5 Number of yellow spins 6 7 2 8 9

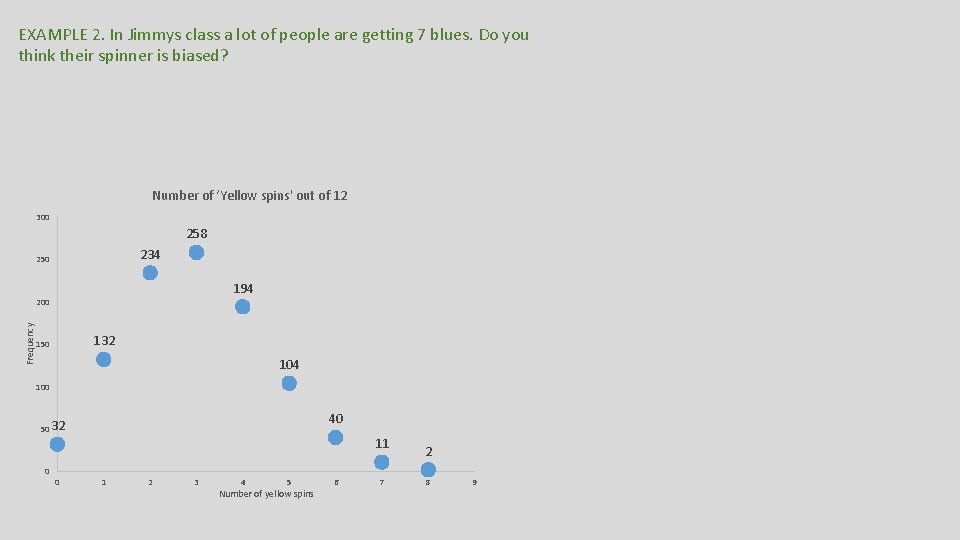
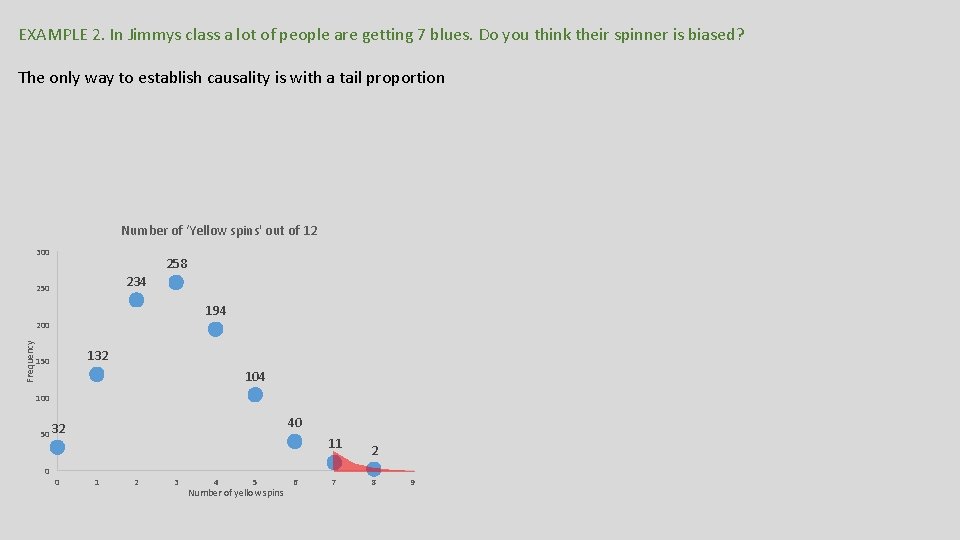
EXAMPLE 2. In Jimmys class a lot of people are getting 7 blues. Do you think their spinner is biased? Number of ‘Yellow spins' out of 12 300 258 234 250 194 Frequency 200 132 150 104 100 40 50 32 11 0 0 1 2 3 4 5 Number of yellow spins 6 7 2 8 9

EXAMPLE 2. In Jimmys class a lot of people are getting 7 blues. Do you think their spinner is biased? The only way to establish causality is with a tail proportion Number of ‘Yellow spins' out of 12 300 258 234 250 194 Frequency 200 132 150 104 100 40 50 32 0 0 11 1 2 3 4 5 Number of yellow spins 6 7 2 8 9

[tail proportion quoted] [tail propiortion in context] [Is that above/below 5%] [therefore it is possible chance alone caused this/therefore it is unlikely that chance alone caused this] [Make a call or do not make a call establishing causality] Number of ‘Yellow spins' out of 12 300 258 234 250 194 Frequency 200 132 150 104 100 40 50 32 0 0 11 1 2 3 4 5 Number of yellow spins 6 7 2 8 9

If we look at the graph, we can see there is a 15. 7% chance of getting a 5 or greater. If we look at the graph, we can see there is a 1. 3% chance of getting a 7 or greater. So, there is a 15. 5% chance that 5, or even greater than 5, yellows will be spun, due to CHANCE ALONE. So, there is a 1. 3% chance that 7, or even greater than 7, yellows will be spun, due to CHANCE ALONE. This is over 5%, and it is possible that chance ALONE can cause this. I cannot make the call that there is anything non-random with the spinner This is below 5%, and it is unlikely that chance ALONE would produce a result like this. Therefore I can make the call that there is something non-random about the spinner, and perhaps it could be weighted funny Number of ‘Yellow spins' out of 12 300 258 234 250 194 Frequency 200 BUT WHY 5% Where did that come from? 132 150 104 100 40 50 32 0 0 11 1 2 3 4 5 Number of yellow spins 6 7 2 8 9

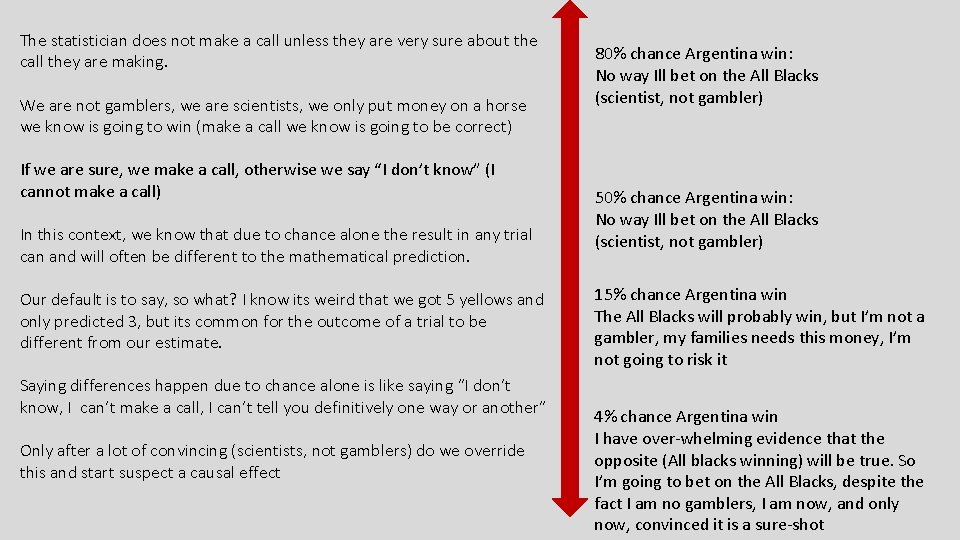
The statistician does not make a call unless they are very sure about the call they are making. We are not gamblers, we are scientists, we only put money on a horse we know is going to win (make a call we know is going to be correct) If we are sure, we make a call, otherwise we say “I don’t know” (I cannot make a call) In this context, we know that due to chance alone the result in any trial can and will often be different to the mathematical prediction. Our default is to say, so what? I know its weird that we got 5 yellows and only predicted 3, but its common for the outcome of a trial to be different from our estimate. Saying differences happen due to chance alone is like saying “I don’t know, I can’t make a call, I can’t tell you definitively one way or another” Only after a lot of convincing (scientists, not gamblers) do we override this and start suspect a causal effect 80% chance Argentina win: No way Ill bet on the All Blacks (scientist, not gambler) 50% chance Argentina win: No way Ill bet on the All Blacks (scientist, not gambler) 15% chance Argentina win The All Blacks will probably win, but I’m not a gambler, my families needs this money, I’m not going to risk it 4% chance Argentina win I have over-whelming evidence that the opposite (All blacks winning) will be true. So I’m going to bet on the All Blacks, despite the fact I am no gamblers, I am now, and only now, convinced it is a sure-shot

50% chance 5 yellow (or greater) under chance alone No way Ill bet against chance alone, this happens regularly even when the trials run are absolutely random 12% chance 5 yellows (or greater) under chance alone There is a pretty low chance of this kind of deviation being created by chance alone, BUT despite that, it is not enough for me to bet against it (scientist, not gambler). People’s lives may be at risk, we will not risk establishing causality And so we stick to our default, and say this finding could be caused by chance/randomness alone (I don’t know) 3% chance 5 yellows (or greater) under chance alone The chance of this deviation happening by chance alone is so low (possible, but rarer than rare) that there is evidence of the opposite, that it is not just chance alone, but some causal effect that is contributing as well. It is now and only now that we leave our default and assert that chance must have been aided by something else to get a result this extreme So, when we consider how many simulations came with 5 yellows or greater

CHANCE VARIATION RECAP RADNOMNESS What is it? PITFALLS Patterns without Uncertainty Vs Uncertainty without Patterns UNDERSTANDIN G SIMULATIONS Patterns emerge over 1000 trials NOT 1000 random numbers CHANCE ALONE OR CAUSALITY Students need to understand that causality means there has been a non -random effect on our situation. TAIL This can only be explored PROPORTION through the tail proportion

(EXTENSION FROM PROBABILITY DISTRIBUTIONS) For example. It is found that a lot of people who play the game get 5 blue spins. Do you think the spinner is biased? One of the ways we can test this is through a theoretical model. Here the binomial would be best. • • Fixed number of trials (12 spins) 2 outcomes (spin a blue or don’t) Probability of success remains constant (0. 25) Independent (the outcome in one spin has no bearing on the outcome in the next spin) Again, when you use the Binomial model in the calculator it REQUIRES that probability of success is 0. 25. So AGAIN, calculations are made under the strict requirement of the spinner being ‘fair’ (0. 25 chance of spinning a blue). P(X >= 5) =0. 1576. So there is a 15. 76% likelihood that chance variation BY ITSELF would create a shift this big. Can’t discount that getting 5 or greater would be created by chance alone (but right a full summary as was taught in the earlier slides)