Teacher Mrs Volynskaya Algebra 2 Absolute Value Equations

Teacher – Mrs. Volynskaya Algebra 2 Absolute Value Equations Absolute value A numbers distance from 0 on number line. ALWAYS POSITIVE!!! n Extraneous Solution A solution that appears to be a solution, but doesn’t work in the original equation. n

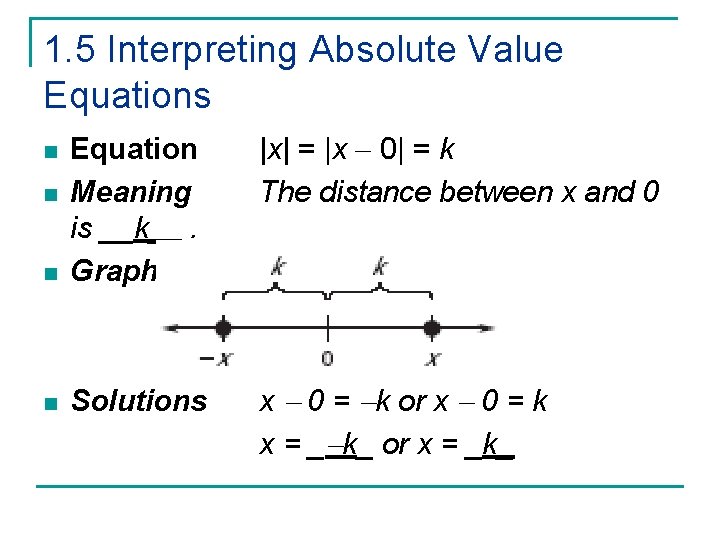
1. 5 Interpreting Absolute Value Equations |x| = |x 0| = k The distance between x and 0 n Equation Meaning is __k__. Graph n Solutions x 0 = k or x 0 = k x = _ k_ or x = _k_ n n

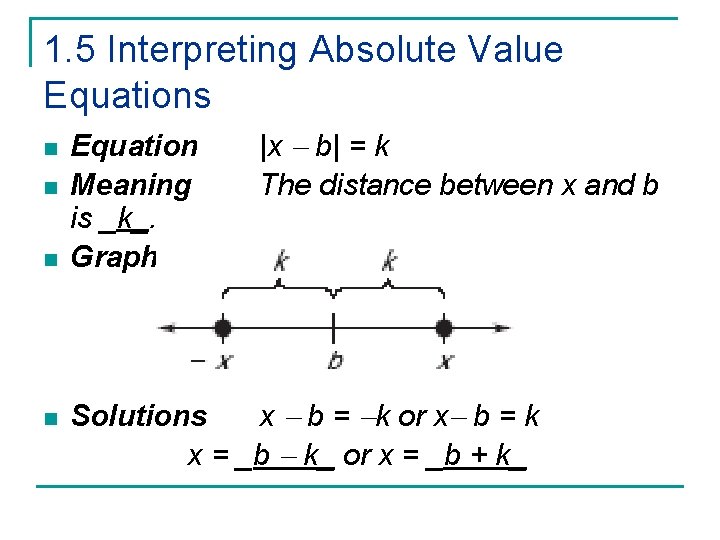
1. 5 Interpreting Absolute Value Equations n n Equation Meaning is _k_. Graph |x b| = k The distance between x and b Solutions x b = k or x b = k x = _b k_ or x = _b + k_

Teacher – Mrs. Volynskaya Algebra 2 1. 5 Solving an absolute value equation Use these steps to solve an absolute value equation | ax + b | = c where c > 0. Step 1 Write two equations: ax + b = _c_ or ax + b = _ c__. n Step 2 Solve each equation. n Step 3 Check each solution in the original _absolute value_ equation. n

Example 1 Solve a simple absolute value equation Solve |x 3 | = 6. Graph the solution. x 3 = -6 or x 3 = 6 +3 +3 x = -3 x=9 These are the values that are 6 from 3 on the number line. n

Example 2 Solve an absolute value equation n Solve |4 x + 10 | = 6 x. Check for extraneous solutions. 4 x + 10 = 6 x or 4 x + 10 = -6 x -4 x -4 x 10 = 2 x 10 = -10 x 10/2 = 2 x/2 10/-10 = -10 x/-10 5=x -1 = x CHECK

Example 2 Solve an absolute value equation n Check |4 x + 10 | = 6 x |4(_5_) + 10| ≟ 6(_5_) |4( 1_ ) + 10 | ≟ 6(_ 1_) |_30_| ≟ _30_ |_6_| ≟ _ 6_ _30_ = _30_ _6_ _ 6_ X=5 x = -1 is rejected, because it is an extraneous solution.

1. 5 Absolute Value Inequalities n Inequality Equivalent Form |ax + b| _<_ c c < ax + b < c n Graph of Solution n Inequality |ax + b| _>_ c n Graph of Solution Equivalent Form ax + b < c or ax + b > c

Example 3 Solve an inequality n Solve |2 x + 5 | > 3. Then graph the solution. 2 x + 5 < -3 or 2 x + 5 > 3 -5 -5 2 x < -8 2 x > -2 2 x/2 < -8/2 2 x/2 > -2/2 x < -4 x > -1

Example 4 Solve an inequality n Solve |x 1. 5| 4. 5. Then graph the solution. x – 1. 5 ≤ 4. 5 or x – 1. 5 ≥ -4. 5 +1. 5 x≤ 6 x ≥ -3