Teach A Level Vol 1 AS Core Maths

















- Slides: 27

“Teach A Level Vol. 1: AS Core Maths” Modules 8: Simultaneous Equations and Intersections © Christine Crisp

Simultaneous Equations and Intersections Module C 1 "Certain images and/or photos on this presentation are the copyrighted property of Jupiter. Images and are being used with permission under license. These images and/or photos may not be copied or downloaded without permission from Jupiter. Images"

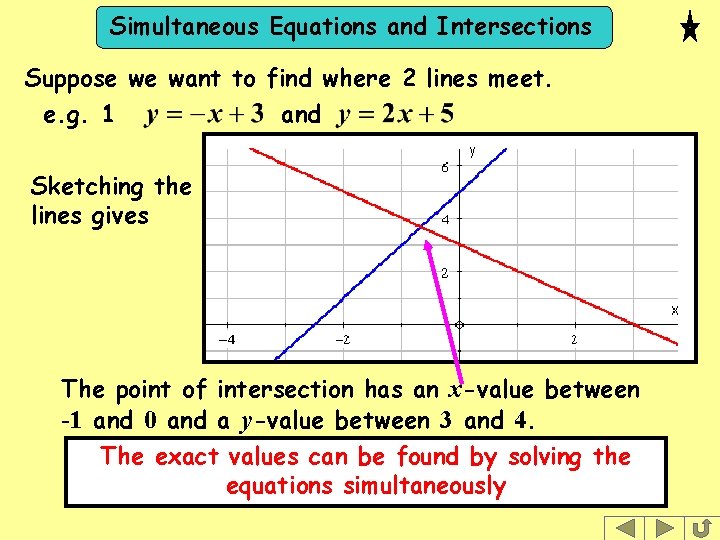
Simultaneous Equations and Intersections Suppose we want to find where 2 lines meet. e. g. 1 and Sketching the lines gives The point of intersection has an x-value between -1 and 0 and a y-value between 3 and 4. The exact values can be found by solving the equations simultaneously

Simultaneous Equations and Intersections At the point of intersection, we notice that the x-values on both lines are the same and the yvalues are also the same. As the y-values are the same, the right-hand sides of the equations must also be the same. Substituting into one of the original equations, we can find y: The point of intersection is

Simultaneous Equations and Intersections Sometimes the equations first need to be rearranged: e. g. 2 Solution: Equation (2) can be written as Now, eliminating y between (1) and (2 a) gives: Substituting into (1): The point of intersection is

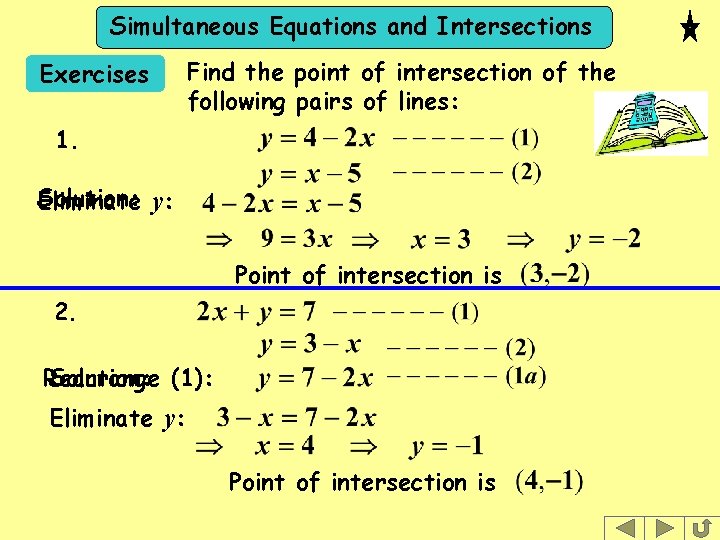
Simultaneous Equations and Intersections Exercises Find the point of intersection of the following pairs of lines: 1. Solution: y: Eliminate Point of intersection is 2. Rearrange Solution: (1): Eliminate y: Point of intersection is

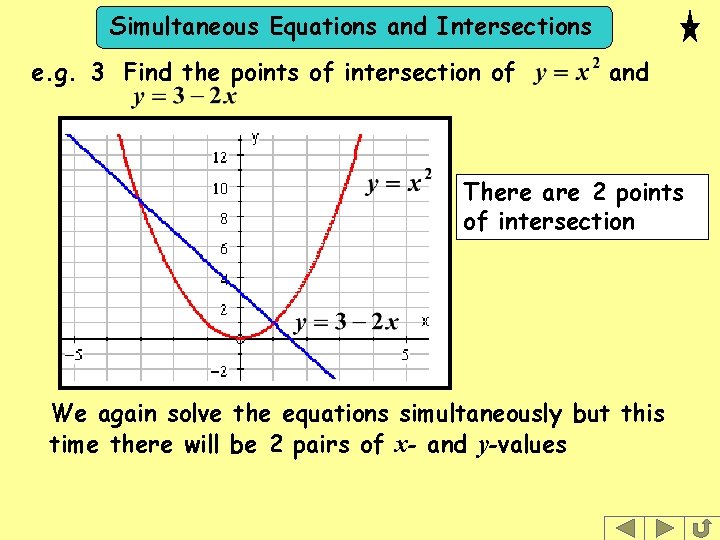
Simultaneous Equations and Intersections e. g. 3 Find the points of intersection of and There are 2 points of intersection We again solve the equations simultaneously but this time there will be 2 pairs of x- and y-values

Simultaneous Equations and Intersections e. g. 1 Since the y-values are equal we can eliminate y by equating the right hand sides of the equations: This is a quadratic equation, so we get zero on one side and try to factorise: To find the y-values, we use the linear equation, which in this example is equation (2) The points of intersection are (1, 1) and (-3, 9)

Simultaneous Equations and Intersections Sometimes we need to rearrange the linear equation before eliminating y e. g. 2 Rearranging (2) gives Eliminating y: or Substituting in (2 a):

Simultaneous Equations and Intersections Exercise Find the points of intersections of the following curve and line The solution is on the next slide

Simultaneous Equations and Intersections Solution: Rearrange (2): Eliminate y: Substitute in (2 a): The points of intersection are

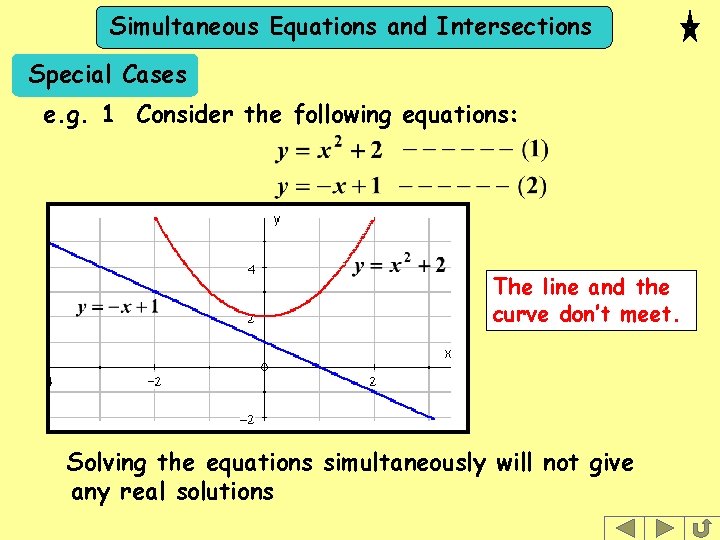
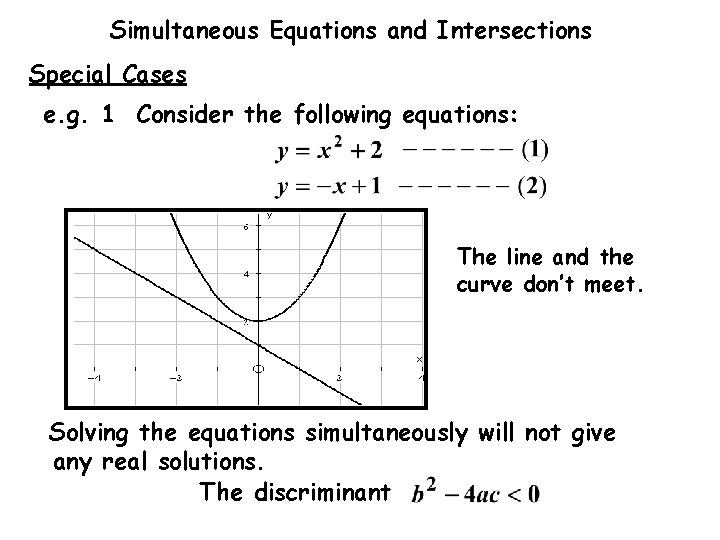
Simultaneous Equations and Intersections Special Cases e. g. 1 Consider the following equations: The line and the curve don’t meet. Solving the equations simultaneously will not give any real solutions

Simultaneous Equations and Intersections Suppose we try to solve the equations: Eliminate y: Calculating the discriminant, we get: The quadratic equation has no real roots.

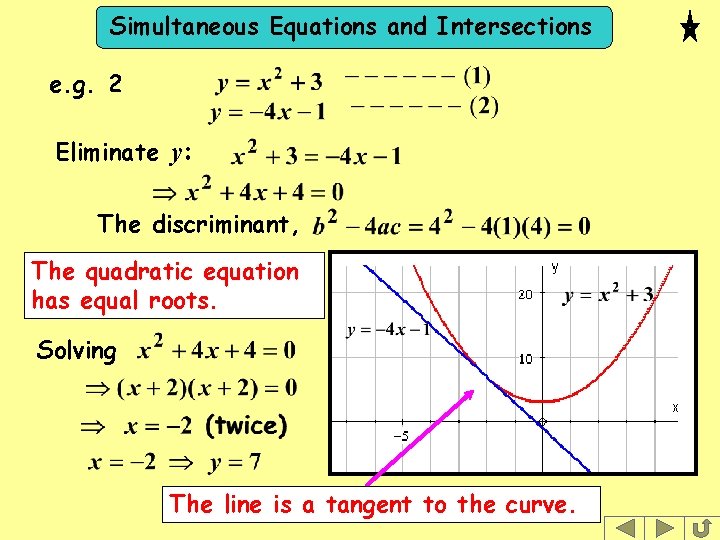
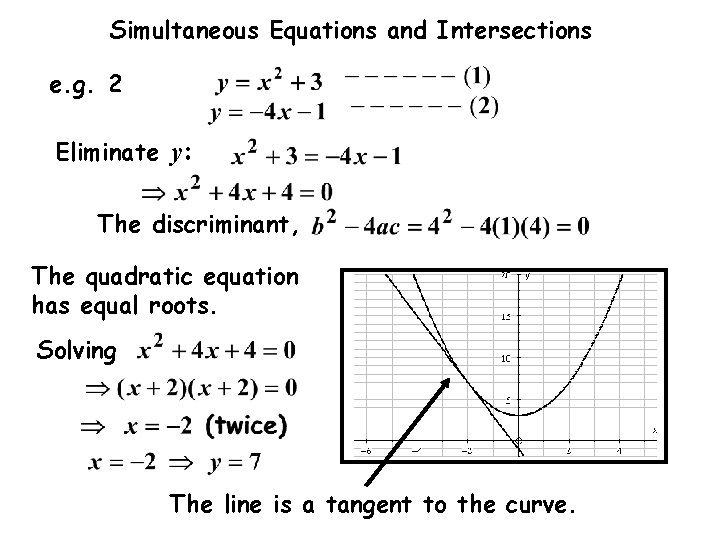
Simultaneous Equations and Intersections e. g. 2 Eliminate y: The discriminant, The quadratic equation has equal roots. Solving The line is a tangent to the curve.

Simultaneous Equations and Intersections SUMMARY Ø A linear and a quadratic equation represent a line and a curve. Ø To solve a linear and a quadratic equation simultaneously: • Eliminate one unknown to give a quadratic equation in the 2 nd unknown, e. g. 2 points of intersection • • the line is a tangent to the curve Substitute into the linear equation to find the values of the 1 st unknown. Solve for the 2 nd unknown the line and curve do not meet and the equations have no real solutions.

Simultaneous Equations and Intersections Exercises Decide whether the following pairs of lines and curves meet. If they do, find the point(s) of intersection. For each pair, sketch the curve and line. 1. 2. 3.

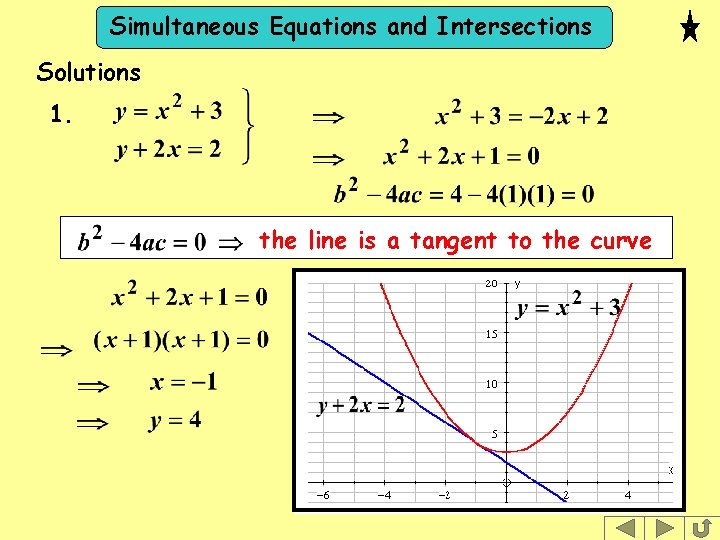
Simultaneous Equations and Intersections Solutions 1. the line is a tangent to the curve

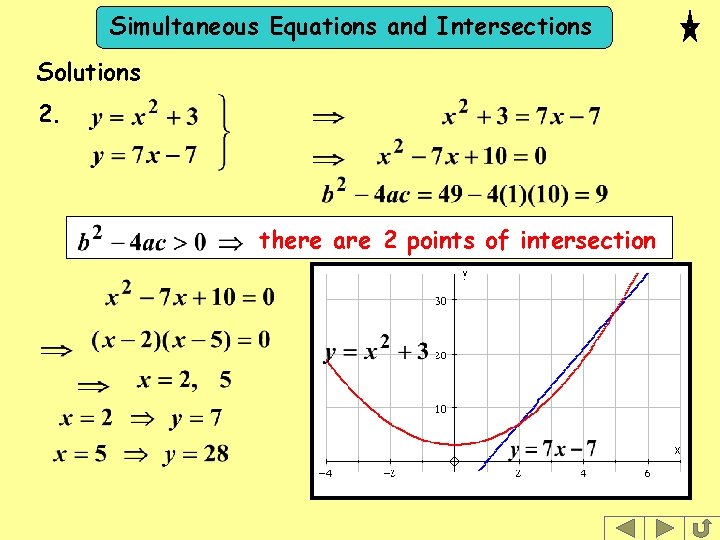
Simultaneous Equations and Intersections Solutions 2. there are 2 points of intersection

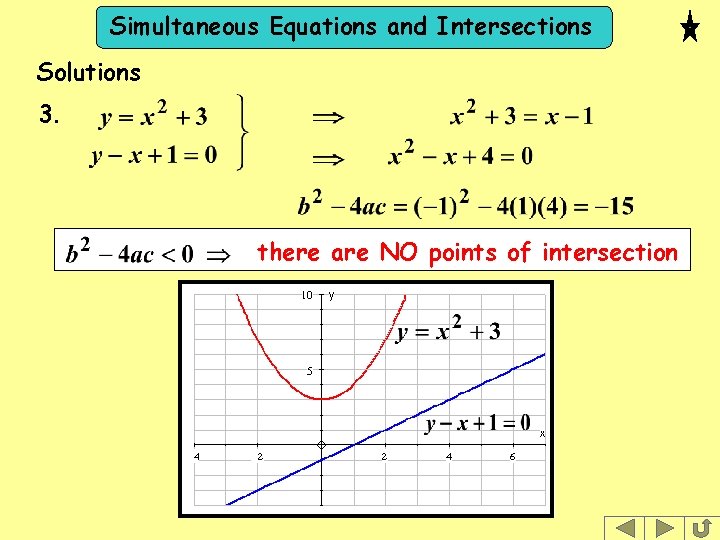
Simultaneous Equations and Intersections Solutions 3. there are NO points of intersection

Simultaneous Equations and Intersections

Simultaneous Equations and Intersections The following slides contain repeats of information on earlier slides, shown without colour, so that they can be printed and photocopied. For most purposes the slides can be printed as “Handouts” with up to 6 slides per sheet.

Simultaneous Equations and Intersections Two Lines At the point of intersection, we notice that the x-values on both lines are the same and the y-values are the same. As the y-values are the same, the righthand sides of the equations must also be the same. Substituting into one of the original equations, we can find y: The point of intersection is

Simultaneous Equations and Intersections 1 quadratic equation and 1 linear equation e. g. Since the y-values are equal we can eliminate y by equating the right hand sides of the equations: This is a quadratic equation, so we get zero on one side and try to factorise: To find the y-values, we use the linear equation, which in this example is equation (2) The points of intersection are (1, 1) and (-3, 9)

Simultaneous Equations and Intersections Sometimes we need to rearrange the linear equation before eliminating y e. g. Rearranging (2) gives Eliminating y: or Substituting in (2 a):

Simultaneous Equations and Intersections Special Cases e. g. 1 Consider the following equations: The line and the curve don’t meet. Solving the equations simultaneously will not give any real solutions. The discriminant

Simultaneous Equations and Intersections e. g. 2 Eliminate y: The discriminant, The quadratic equation has equal roots. Solving The line is a tangent to the curve.

Simultaneous Equations and Intersections SUMMARY Ø A linear and a quadratic equation represent a line and a curve. Ø To solve a linear and a quadratic equation simultaneously: • Eliminate one unknown to give a quadratic equation in the 2 nd unknown, e. g. 2 points of intersection • • the line is a tangent to the curve Substitute into the linear equation to find the values of the 1 st unknown. Solve for the 2 nd unknown the line and curve do not meet and the equations have no real solutions.