Teach A Level Maths Vol 1 AS Core

“Teach A Level Maths” Vol. 1: AS Core Modules 50: Harder Indefinite Integration © Christine Crisp

Indefinite Integration Module C 2 "Certain images and/or photos on this presentation are the copyrighted property of Jupiter. Images and are being used with permission under license. These images and/or photos may not be copied or downloaded without permission from Jupiter. Images"

Indefinite Integration Reminder: • • • add 1 to the power divide by the new power add C n does not need to be an integer BUT notice that the rule is for It cannot be used directly for terms such as

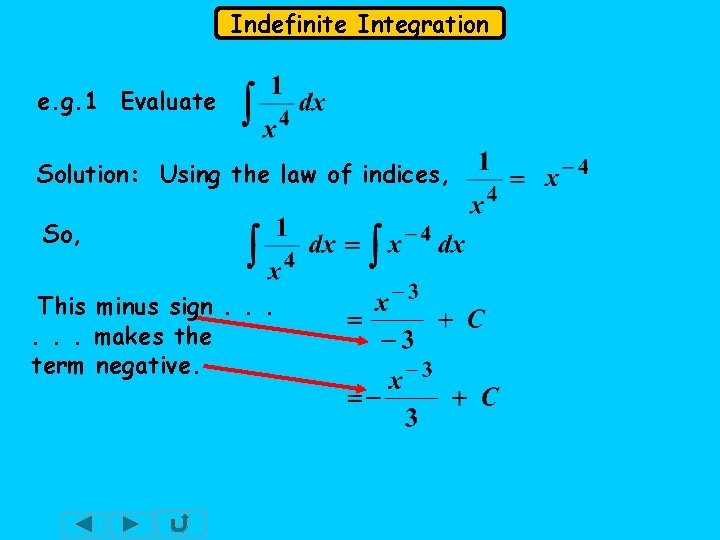
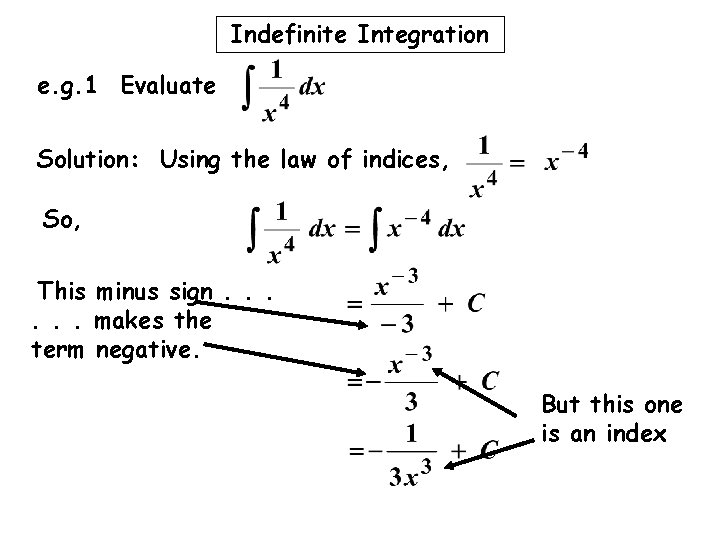
Indefinite Integration e. g. 1 Evaluate Solution: Using the law of indices, So, This minus sign. . . makes the term negative.

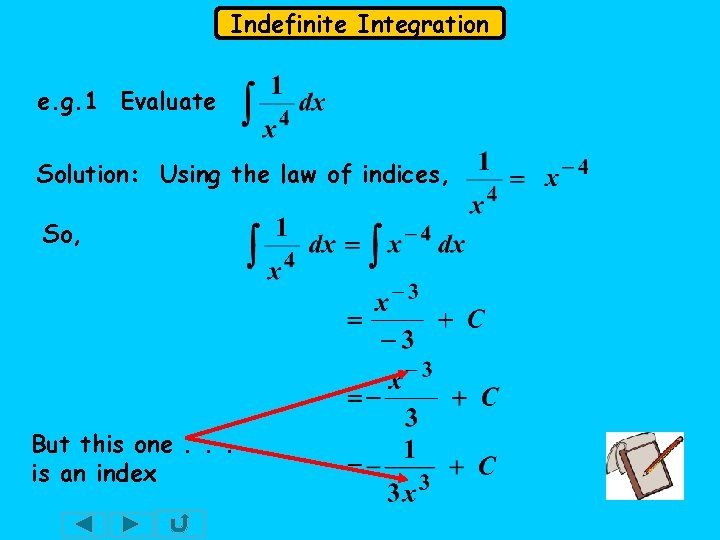
Indefinite Integration e. g. 1 Evaluate Solution: Using the law of indices, So, But this one. . . is an index

Indefinite Integration e. g. 2 Evaluate Solution: We need to simplify this “piled up” fraction. Multiplying the numerator and denominator by 2 gives We can get this answer directly by noticing that. . . dividing by a fraction is the same as multiplying by its reciprocal. ( We “flip” the fraction over ).

Indefinite Integration e. g. 2 Evaluate Solution: We need to simplify this “piled up” fraction. Multiplying the numerator and denominator by 2 gives We can get this answer directly by noticing that. . . dividing by a fraction is the same as multiplying by its reciprocal. ( We “flip” the fraction over ).

Indefinite Integration e. g. 3 Evaluate Solution: So, Using the law of indices,

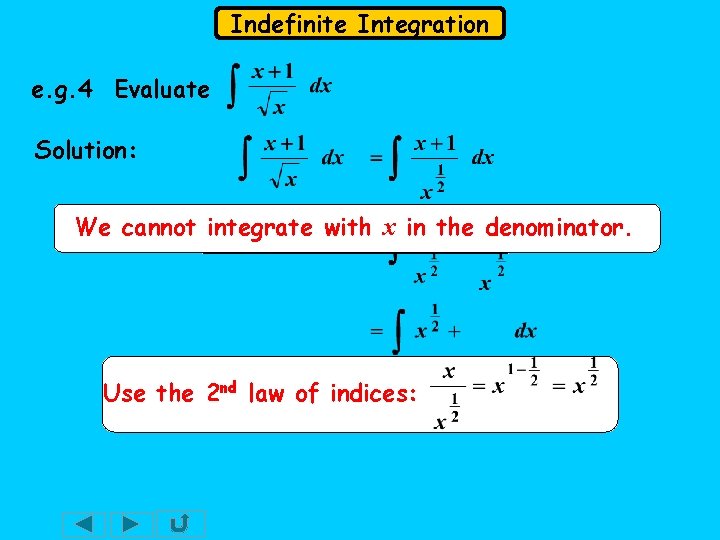
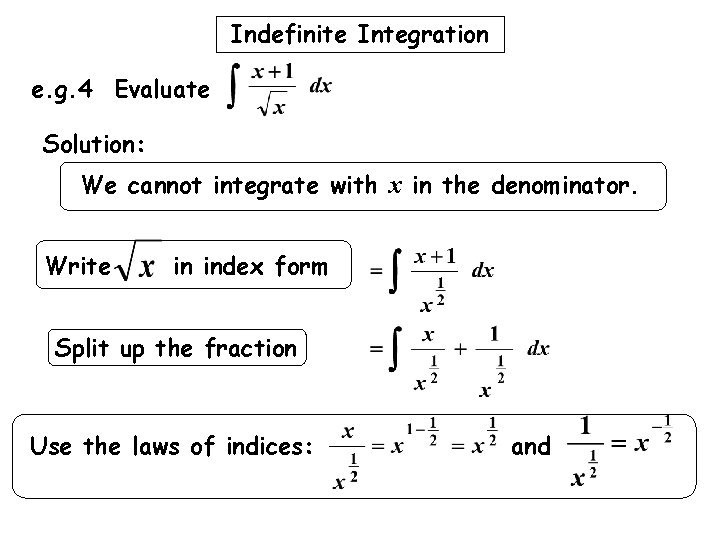
Indefinite Integration e. g. 4 Evaluate Solution: We cannot Split integrate with x in the up the Write infraction index formdenominator. Use the 2 nd law of indices:

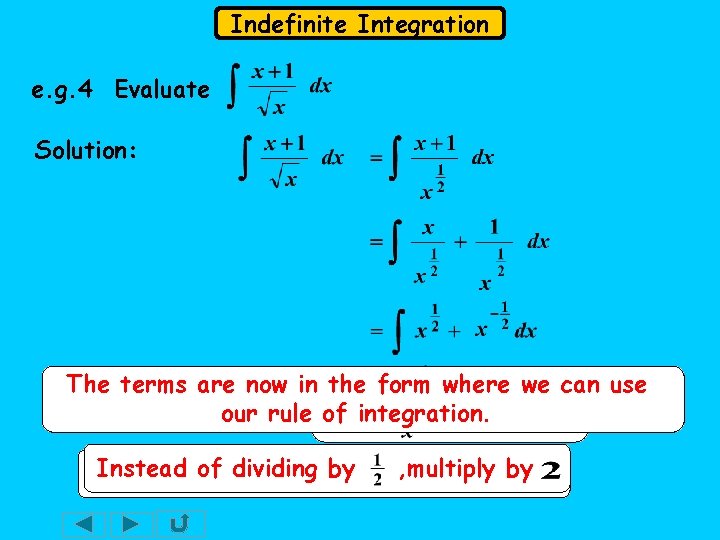
Indefinite Integration e. g. 4 Evaluate Solution: The terms are now in the form where we can use and our rule of integration. Instead of of dividing by by Instead , multiply by by , multiply

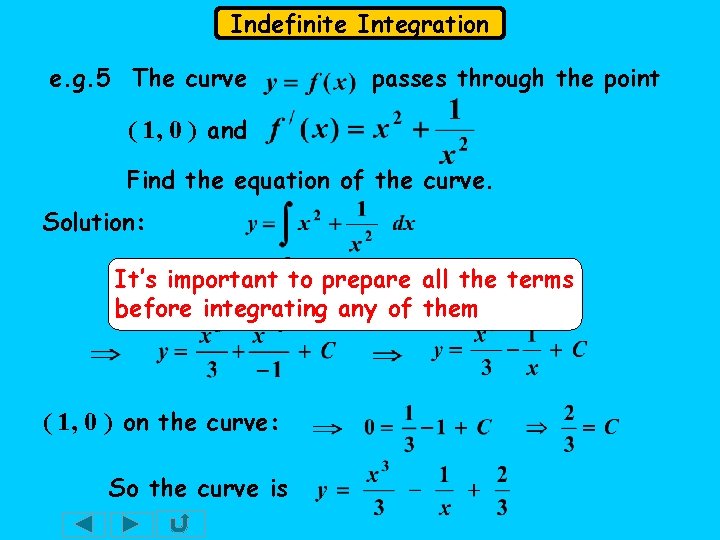
Indefinite Integration e. g. 5 The curve passes through the point ( 1, 0 ) and Find the equation of the curve. Solution: It’s important to prepare all the terms before integrating any of them ( 1, 0 ) on the curve: So the curve is

Indefinite Integration Exercise Evaluate 1. Solution: 2.

Indefinite Integration Exercise 3. Given that , find the equation of the curve through the point ( 1, 0 ). Solution: ( 2, 0 ) on the curve: So the curve is

Indefinite Integration

Indefinite Integration The following slides contain repeats of information on earlier slides, shown without colour, so that they can be printed and photocopied. For most purposes the slides can be printed as “Handouts” with up to 6 slides per sheet.

Indefinite Integration e. g. 1 Evaluate Solution: Using the law of indices, So, This minus sign. . . makes the term negative. But this one is an index

Indefinite Integration e. g. 2 Evaluate Solution: We need to simplify this “piled up” fraction. Multiplying the numerator and denominator by 2 gives We can get this answer directly by noticing that. . . dividing by a fraction is the same as multiplying by its reciprocal. ( We “flip” the fraction over ).

Indefinite Integration e. g. 3 Evaluate Solution: So, Using the law of indices,

Indefinite Integration e. g. 4 Evaluate Solution: We cannot integrate with x in the denominator. Write in index form Split up the fraction Use the laws of indices: and

Indefinite Integration The terms are now in the form where we can use our rule of integration.

Indefinite Integration e. g. 5 The curve ( 1, 0 ) and passes through the point. Find the equation of the curve. Solution: It’s important to prepare all the terms before integrating any of them ( 1, 0 ) on the curve: So the curve is