TB week 1 Wachtrijtheorie en Simulatie Waarom duurt

TB week 1: Wachtrijtheorie en Simulatie Waarom duurt wachten lang en wat kunnen we er aan doen met simulatie Alexander Verbraeck Sectie Systeemkunde 7 september 2011 1

Wachtrijen. . . • Op de weg (net te laat weg, en dan loop je vast) • In de supermarkt (en dan net de verkeerde rij kiezen) • Bij het call-centrum via de telefoon (er zijn nog 68 wachtenden voor u. . . ) • In de kantine (helaas te laat voor de lekkere broodjes) • In de fabriek (onderdelen die op verwerking liggen te wachten) • Op kantoor (stapels dossiers en lijsten met e-mails die nog afgehandeld moeten worden) • Vliegtuigen die rondcirkelen voordat ze kunnen landen 7 september 2011 2

Waarom wachtrijen? • Waar komen de wachtrijen vandaan en waarom zijn ze zo hardnekkig? • Waarom zijn de wachtrijen vaak langer dan wat we op grond van ons ‘gevoel’ zouden zeggen? • Hoe goed kunnen we het optreden van wachtrijen voorspellen? • Er is theorie over wachtrijen • We kunnen wachtrijen simuleren • We kunnen de opgedane kennis toepassen 7 september 2011 3

Hoe goed snappen we wachten (1)? • Stel dat we de tram met een frequentie volgens de dienstregeling van eens per 10 minuten willen nemen, maar we wonen halverwege het tracé, dus met alle verstoringen gedraagt de tram zich alsof hij geheel willekeurig aankomt. Gemiddeld komen er wel 6 trams per uur, maar soms zit er een groot gat, en soms zitten er twee vlak achter elkaar. • Stel ik kom op de halte aan, en ik zie daar iemand staan die zegt dat zij al 10 minuten wacht. Hoe lang moet ik dan gemiddeld nog wachten op de tram? 7 september 2011 4

Hoe goed snappen we wachten (2)? • Stel dat we de tram met een frequentie volgens de dienstregeling van eens per 10 minuten willen nemen, maar we wonen halverwege het tracé, dus met alle verstoringen gedraagt de tram zich alsof hij geheel willekeurig aankomt. Gemiddeld komen er wel 6 trams per uur, maar soms zit er een groot gat, en soms zitten er twee vlak achter elkaar. • Stel ik kom op de halte aan, en ik zie daar iemand staan die zegt dat zij al 10 minuten wacht. Hoe lang moet ik dan gemiddeld nog wachten op de tram? • Antwoord: gemiddeld 10 minuten. . . 7 september 2011 5

Hoe goed ‘snappen’ we wachten (3)? • Stel, we hebben een balie met 5 medewerkers, die elk 10 mensen per uur kunnen helpen. Er komen gemiddeld 48 mensen per uur binnen. Ze kunnen het dus makkelijk aan. Hoe lang is: de gemiddelde wachtrij? de gemiddelde wachttijd? komt de wachtrij wel eens boven de 20? boven de 10? boven de 5? 7 september 2011 6

Hoe goed ‘snappen’ we wachten (4)? • Stel, we hebben een balie met 5 medewerkers, die elk 10 mensen per uur kunnen helpen. Er komen gemiddeld 48 mensen per uur binnen. Ze kunnen het dus makkelijk aan. Hoe lang is: de gemiddelde wachtrij de gemiddelde wachttijd komt de wachtrij wel eens boven de 20 boven de 10 boven de 5 7 september 2011 13 16 min. JA VAAK 7

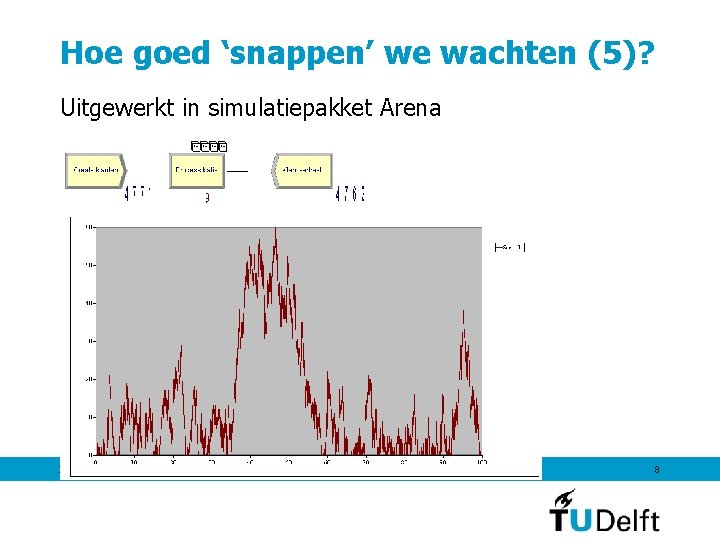
Hoe goed ‘snappen’ we wachten (5)? Uitgewerkt in simulatiepakket Arena 7 september 2011 8

Wachten in één rij of meer rijen (1) • Soms is er één wachtrij bij meer ‘loketten’, b. v. veiligheidsscan op sommige luchthavens • Soms heeft elk ‘loket’ een eigen wachtrij, b. v. kassa’s bij de supermarkt • • Maakt dat verschil? Wat is ‘eerlijker’? Verschilt de gemiddelde wachttijd? Waarom? 7 september 2011 9

Wachten in één rij of meer rijen (2) • Soms is er één wachtrij bij meer ‘loketten’, b. v. veiligheidsscan op sommige luchthavens • Soms heeft elk ‘loket’ een eigen wachtrij, b. v. kassa’s bij de supermarkt • • Maakt dat verschil? JA Wat is ‘eerlijker’? 1 rij Verschilt de gemiddelde wachttijd? Waarom? Lege rij 7 september 2011 JA 10

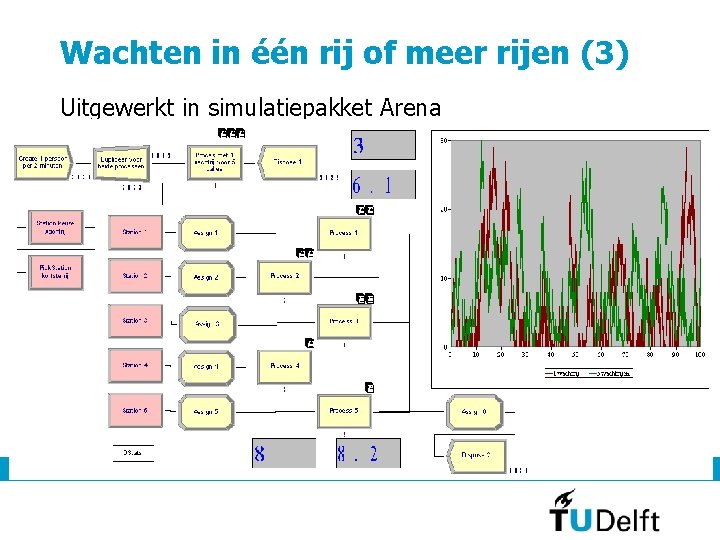
Wachten in één rij of meer rijen (3) Uitgewerkt in simulatiepakket Arena 7 september 2011 11

Telefonische diensten (1) • Als je een telefonische dienst belt, moet je vaak keuzes maken met nummers voordat je iemand aan de lijn krijgt. • Waarom is dat? • Maakt het verschil in de wachtrijen? • Waarom? 7 september 2011 12

Telefonische diensten (2) • Als je een telefonische dienst belt, moet je vaak keuzes maken met nummers voordat je iemand aan de lijn krijgt. • Waarom is dat? Specialisatie van taken • Maakt het verschil in de wachtrijen? Ja • Waarom? Meer “gelijke” taken per medewerker 7 september 2011 13

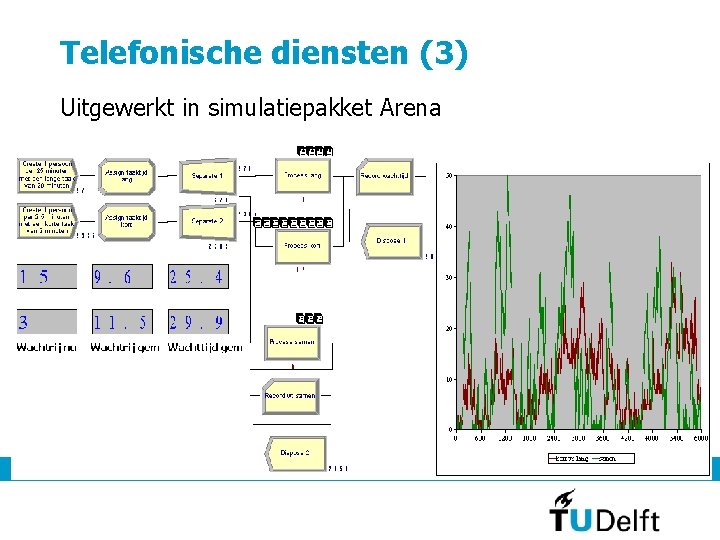
Telefonische diensten (3) Uitgewerkt in simulatiepakket Arena 7 september 2011 14

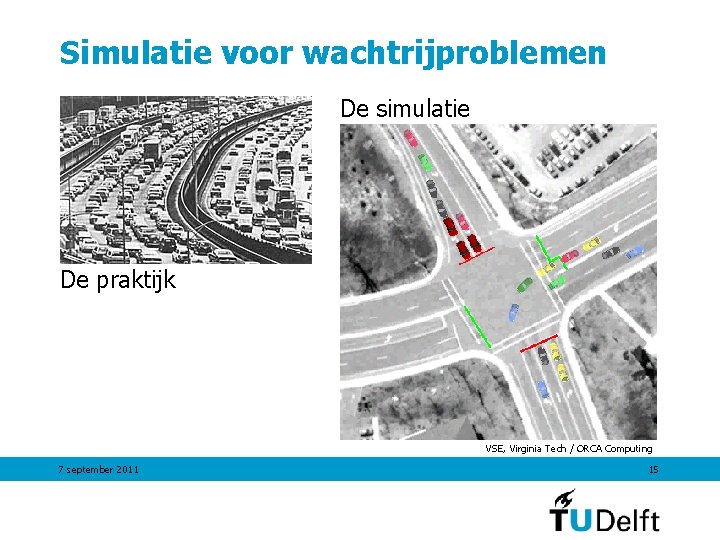
Simulatie voor wachtrijproblemen De simulatie De praktijk VSE, Virginia Tech / ORCA Computing 7 september 2011 15

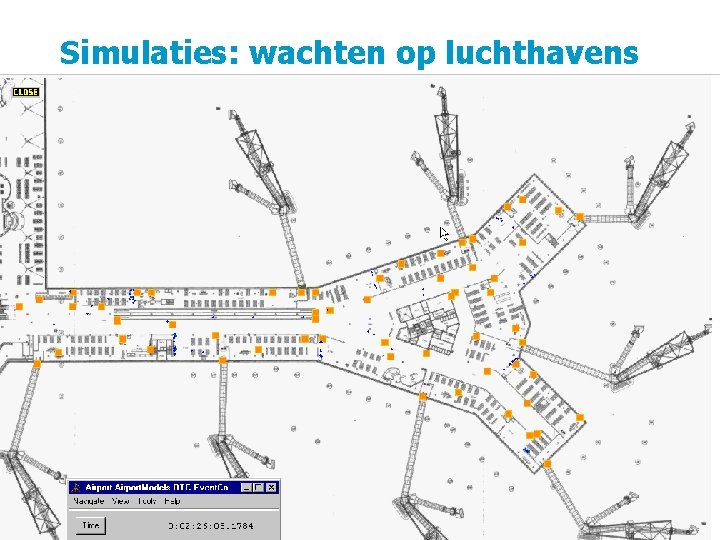
Simulaties: wachten op luchthavens 7 september 2011 16

Model: ARC, Aken, Duitsland Simulatie: wachten bij klaarmaken vliegtuig 7 september 2011 17

Simulatie: Wachten bij instappen Model: ARC, Aken, Duitsland 7 september 2011 18

Simulatie: wachten bij taxiën Model: ARC, Aken, Duitsland 7 september 2011 19

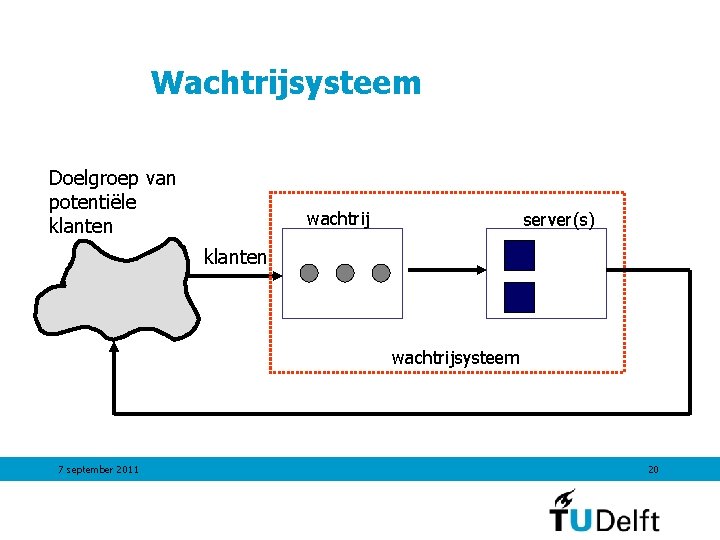
Wachtrijsysteem Doelgroep van potentiële klanten wachtrij server(s) klanten wachtrijsysteem 7 september 2011 20

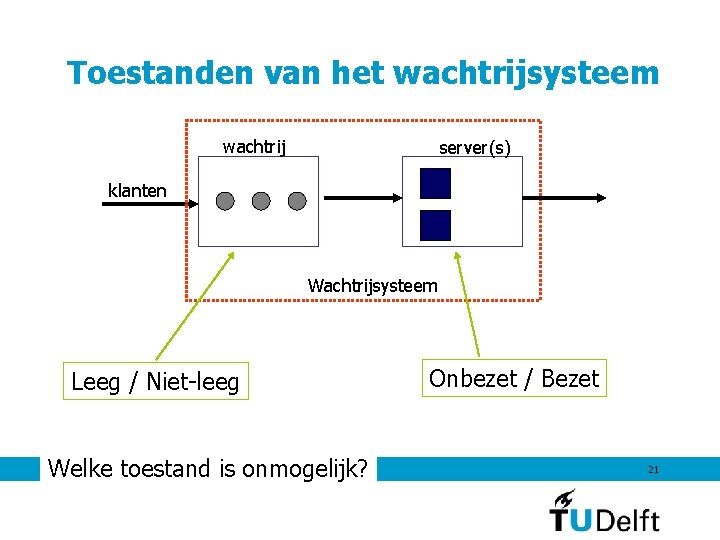
Toestanden van het wachtrijsysteem wachtrij server(s) klanten Wachtrijsysteem Leeg / Niet-leeg 7 september 2011 Welke toestand is onmogelijk? Onbezet / Bezet 21

Parameters van een wachtrijsysteem Prestatie van het wachtrijsysteem is afhankelijk van: • • • Aankomstproces ( en verdeling tussentijd) Bedieningsproces ( en verdeling bedieningstijd) Aantal loketten Capaciteit van wachtrij Capaciteit van het systeem + Aantal servers Omvang van de doelgroep ∞ of niet 7 september 2011 22

Voorbeeld bezettingsgraad Bij de helpdesk van de faculteit: • Gemiddeld arriveren er 4 klanten per uur met een hulpvraag (Poisson) • Gemiddeld kunnen 6 klanten per uur worden geholpen (Poisson) • Wat is de bezettingsgraad (Griekse letter rho) voor • 1 helpdesk medewerker? • 2 helpdesk medewerkers? 7 september 2011 23

Aankomstproces • Aankomsttussentijden stochastisch of deterministisch? • Eén voor één op groepsgewijs? • Groepsgrootte stochastisch of deterministisch • Meestal: • Aantal klanten per tijdseenheid Poisson verdeeld • Tussenaankomsttijden exponentieel verdeeld zelfde! • Eén voor één • Aankomstintensiteit (aantal/tijdseenheid): λ 7 september 2011 24

Bedieningsproces • Bedieningstijden stochastisch of deterministisch? • Bijv. normaal verdeeld of exponentieel verdeeld? • Volgorde van bediening • Eerste eerst? • Laatste eerst? • Snelste eerst? • Urgentste eerst? • Bedieningsintensiteit (aantal/tijdseenheid): µ 7 september 2011 25

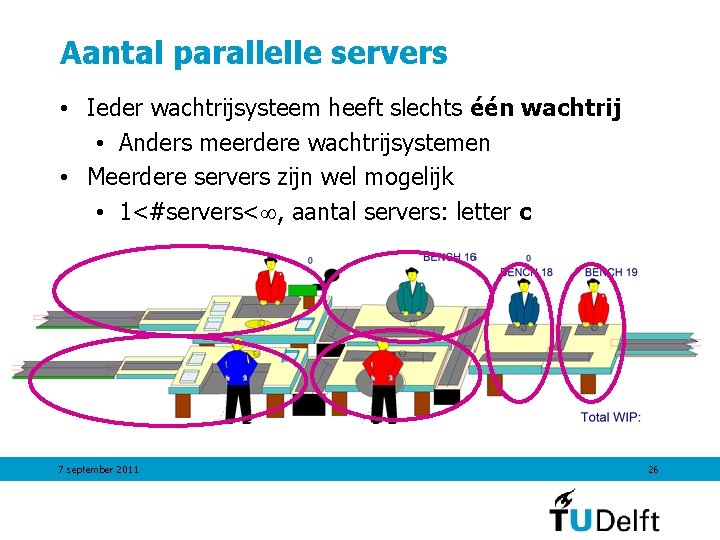
Aantal parallelle servers • Ieder wachtrijsysteem heeft slechts één wachtrij • Anders meerdere wachtrijsystemen • Meerdere servers zijn wel mogelijk • 1<#servers< , aantal servers: letter c 7 september 2011 26

Capaciteit van het systeem • Totale aantal klanten in de wachtrij en bij de loketten • Bij eindige capaciteit • Klanten gaan terug naar doelgroep als wachtrij vol • Effectieve aankomsten Werkelijke aankomsten • Bijvoorbeeld • Bellen van klantenservice (in gesprek bij volle rij) • Numerus fixus voor studie geneeskunde • Opslag in fietsenwinkel 7 september 2011 27

Omvang van de doelgroep • Eindig of oneindig groot? • Oneindig als groep potentiële klanten is groot • Klanten in systeem verwaarloosbaar t. o. v. doelgroep • Restaurant, OV-reisinformatie, Postkantoor, etc. • Eindige doelgroep • Aantal aankomsten hangt af van aantal klanten in systeem • Computers te repareren door de helpdesk, #patiënten op een ziekenhuisafdeling, etc. 7 september 2011 28

Notatie van Kendall A/B/c/N/K waarin: A Verdeling aankomsttussentijd B Verdeling bedieningstijd c Aantal servers N Capaciteit van het systeem K Omvang van de doelgroep Afkortingen verdelingen: M Exponentieel D Constant of deterministisch Ek Erlang G Random of algemeen 7 september 2011 29

Nu een beetje dieper 7 september 2011 30

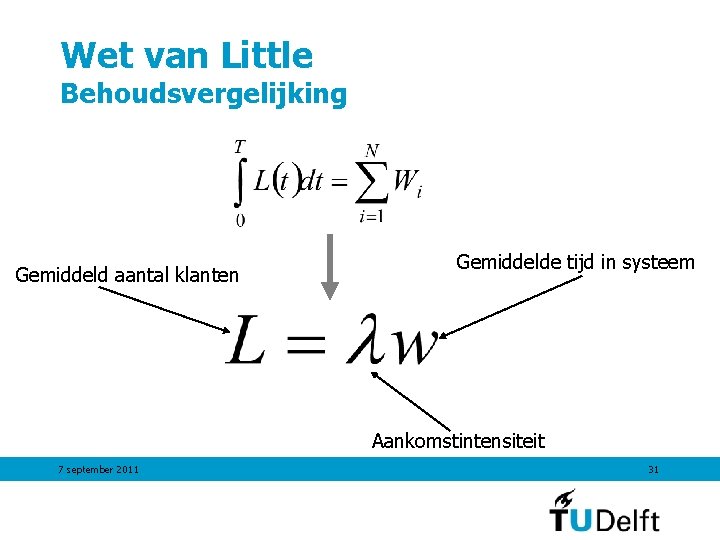
Wet van Little Behoudsvergelijking Gemiddeld aantal klanten Gemiddelde tijd in systeem Aankomstintensiteit 7 september 2011 31

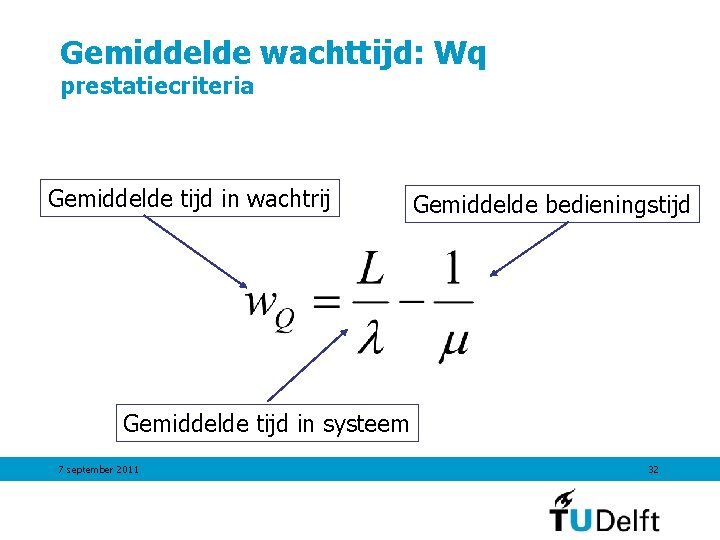
Gemiddelde wachttijd: Wq prestatiecriteria Gemiddelde tijd in wachtrij Gemiddelde bedieningstijd Gemiddelde tijd in systeem 7 september 2011 32

Gemiddelde # klanten in wachtrij: Lq prestatiecriteria Totaal # klanten in systeem Bezettingsgraad server Little’s vergelijking voor de wachtrij 7 september 2011 33

Gemiddeld # klanten in systeem Prestatiecriteria M/M/1 7 september 2011 34

Oefening 1: Kantine met 1 kassa u u u Gemiddeld komt er één klant aan per minuut (Poisson verdeeld) Gemiddelde bedieningstijd is 40 seconde per klant (exponentieel verdeeld) Bepaal … – – – 7 september 2011 Kendall notatie Gemiddelde tijd in systeem? Gemiddelde wachttijd? Gemiddeld aantal klanten in de rij? Kans dat er precies 5 klanten in systeem zijn? 35

Bedieningsproces • Bedieningsvolgorde: • FIFO First In, First Out • LIFO Last In, First Out • SIRO Service In Random Order • SPT Shortest Processing Time first • PR Service according to Priority Wie is er aan de beurt • Bedieningstijden stochastisch of deterministisch? • Bijv. normaal verdeeld of exponentiëel verdeeld? • is de bedieningsintensiteit (bijv. 12 klanten/uur) • 1/ is de gemiddelde bedieningstijd (5 minuten) 7 september 2011 36

Bedieningsvolgorde versus Prestatie wachtrijsysteem • Bedieningsvolgorde heeft geen invloed op • Bezettinggraad • Totale tijd in het systeem • Gemiddelde wachttijd • Totaal aantal klanten in het systeem • Gemiddelde lengte wachtrij • Bedieningsvolgorde heeft alleen invloed op • Variantie van de wachttijd 7 september 2011 37

Oefening 2 • Wat is de klantenvolgorde als bedieningsvolgorde “Shortest processing time first” wordt gebruikt? • Welke andere bedieningsvolgorde zou hetzelfde resultaat geven? • Wat is de gemiddelde wachttijd? (Wq) • Wat is het gemiddeld aantal klanten in de wachtrij? (Lq) Klant Aankomsttijd Bedieningstijd Prioriteit 1 0 2 3 2 1 1 2 3 1. 5 0. 75 4 4 1. 75 0. 5 5 5 2. 75 0. 5 1 7 september 2011 38

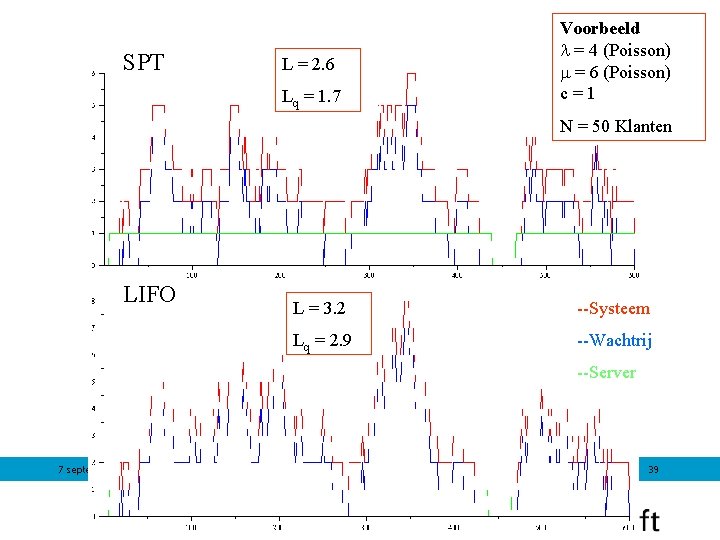
SPT L = 2. 6 Lq = 1. 7 Voorbeeld = 4 (Poisson) = 6 (Poisson) c=1 N = 50 Klanten LIFO L = 3. 2 --Systeem Lq = 2. 9 --Wachtrij --Server 7 september 2011 39

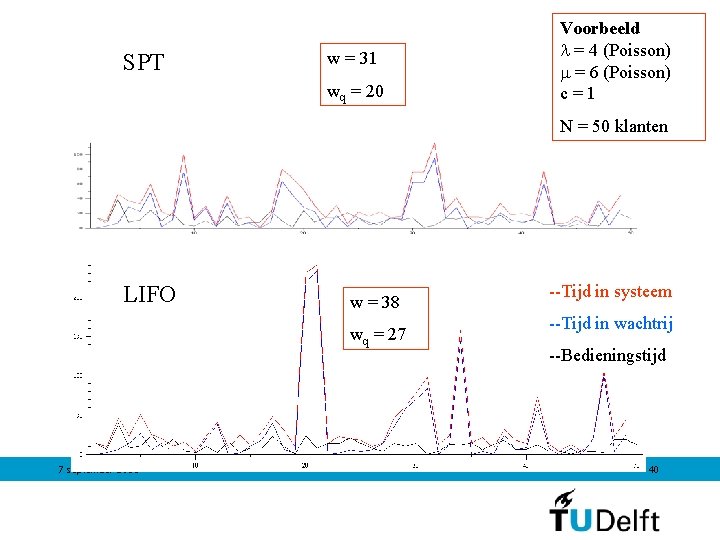
SPT w = 31 wq = 20 Voorbeeld = 4 (Poisson) = 6 (Poisson) c=1 N = 50 klanten LIFO w = 38 wq = 27 7 september 2011 --Tijd in systeem --Tijd in wachtrij --Bedieningstijd 40

Systeem met meer servers. . . bezettingsgraad systeem P 0 kans op 0 klanten in systeem Pn kans op n klanten in systeem L gem. aantal klanten in systeem w gemiddelde tijd dat klant in systeem is w. Q gemiddelde tijd in wachtrij LQ gemiddelde lengte wachtrij L-LQ gem. aantal bezette balies 7 september 2011 41

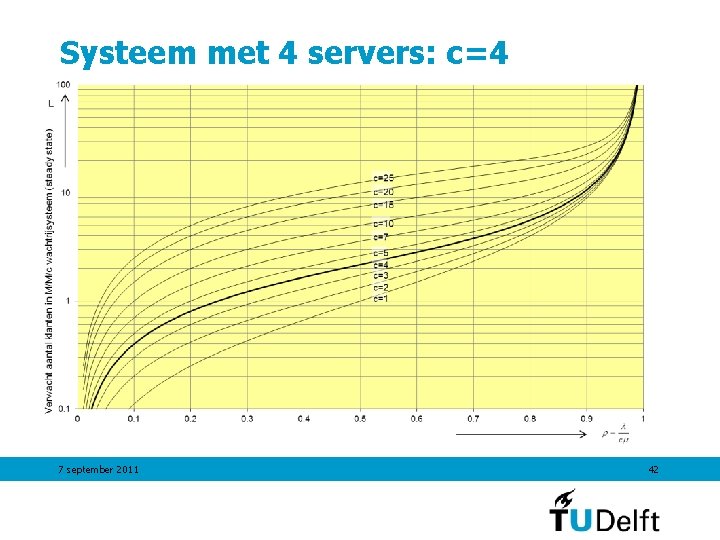
Systeem met 4 servers: c=4 7 september 2011 42

Het systeem met 4 balies in Arena 7 september 2011 43

Berekende waarden 4 balies, =40/uur, =12/uur M/M/4 bezettingsgraad 0. 83 P 0 kans op 0 klanten in systeem 3% L gem. aantal klanten in systeem 5. 5 w gemiddelde tijd dat klant in systeem is 8. 25 min w. Q gemiddelde tijd in wachtrij LQ 5. 5/40 -1/12 = 0. 054 uur = 3. 25 min gemiddelde lengte wachtrij 2. 16 L-LQ gem. aantal bezette balies 7 september 2011 3. 33 44

Simulatie • Met grafen en wachttijdtheorie kunnen bepaalde problemen analytisch worden opgelost maar wat als: • het systeem zo complex is dat het ondoenlijk is de beste oplossing analytisch te berekenen • er veel oplossingen berekend moeten worden en het berekenen veel tijd kost • snel een oplossing nodig is en er geen tijd is voor berekeningen • inzicht verschaft moet worden aan een opdrachtgever over de analyse en de oplossingen • Werkelijkheid TB-problemen is meestal zo complex dat alleen simulatie gebruikt kan worden 7 september 2011 45

Handsimulatie • Kunnen we een dergelijk proces in een wachtrijsysteem ook met de hand uitvoeren? • Laten we een voorbeeld uitproberen met de groep. . . 7 september 2011 46

Voorbeeld Simulatie met de hand Proces in b. v. postkantoor Klanten komen uniform verdeeld aan: • tussentijd discreet tussen 1 en 6 minuten Klanten hebben een bedieningstijd: • 1 op de 6 klanten 1 minuut, • 1 op de 2 klanten 2 minuten, • 1 op de 3 klanten 5 minuten 7 september 2011 47

Bouw van een simulatiemodel • Veel soorten simulatietalen • In 2 e jaar: ARENA (v/a 2012 Simio) uitgebreid behandeld • Andere simulatietalen worden getoond • Voorbeeld: hoe wordt een model van de M/M/c wachtrij met 40 aankomsten per uur, 4 loketten en 5 minuten per bediening gesimuleerd? 7 september 2011 48

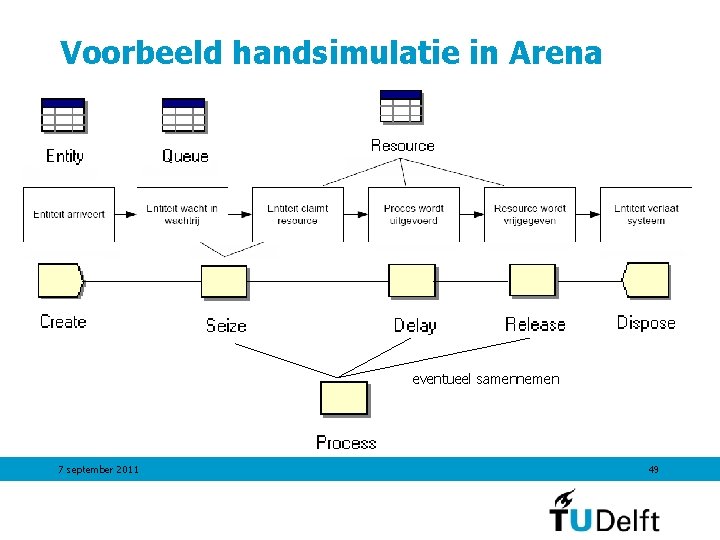
Voorbeeld handsimulatie in Arena eventueel samennemen 7 september 2011 49

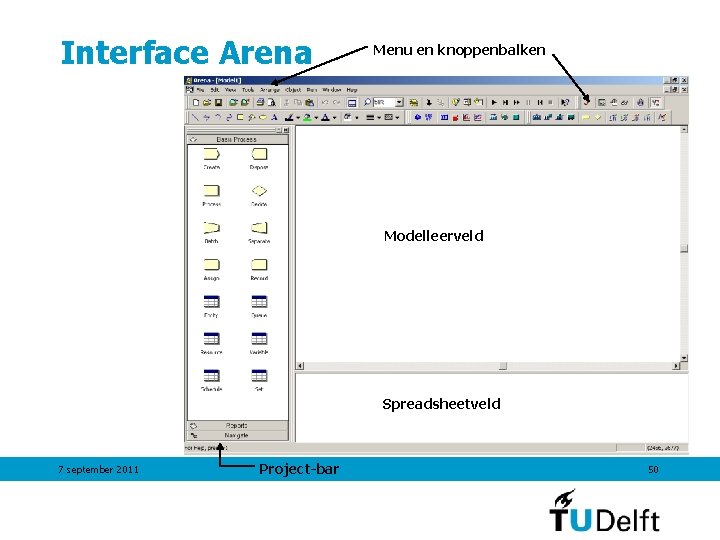
Interface Arena Menu en knoppenbalken Modelleerveld Spreadsheetveld 7 september 2011 Project-bar 50

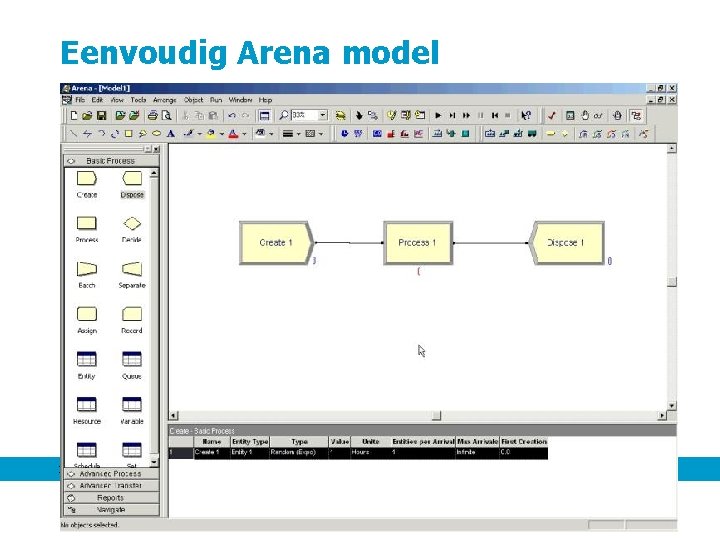
Eenvoudig Arena model 7 september 2011 51

Gesimuleerde waarden 40 aankomsten per uur, 4 loketten en 5 minuten per bediening berekend simulatie bezettingsgraad 0. 83 3. 36/4 = 0. 84 P 0 kans op 0 klanten in systeem 3% - L 5. 5 2. 24+3. 36 = 5. 6 8. 25 min 8. 47 min 3. 25 min 3. 39 min LQ gemiddelde lengte wachtrij 2. 16 2. 24 L-LQ 3. 33 3. 36 gem. aantal klanten in systeem w gemiddelde tijd klant in systeem w. Q gemiddelde tijd in wachtrij 5. 5/40 -1/12 = 0. 054 uur = gem. aantal bezette balies 7 september 2011 52

Gesimuleerde waarden wachtrij Zijn ze precies hetzelfde? Zo nee, waarom niet? Is de simulatie wel valide? Hoe bepalen we dat? Hoe lang moeten we draaien om een bepaalde betrouwbaarheid te bereiken? • Wat is de invloed van de lengte van de simulatie? • Wat is de invloed van het “leeg starten”? • • • 7 september 2011 53

Verkorten wachttijden De theorie leert ons dat de wachttijd verkort kan worden door het: • • • Reduceren aantal aankomsten per tijdseenheid Reduceren bedieningstijd Verhogen aantal servers Verlagen spreiding in aankomsten Verlagen spreiding in bedieningstijd Veranderen van de volgorde voor helpen van klanten 7 september 2011 54

Conclusie wachtrijen en simulatie Murphy heeft gelijk Maar we kunnen er wel wat aan doen! 7 september 2011 55

Wanneer zit dit in het programma? • Basis in het eerste jaar: • analyse • statistiek • modelleertechnieken • Colleges aan het begin van het 2 e jaar • discrete wiskunde • simulatie • Gebruik in 2 e en 3 e jaar • project discreet modelleren • Bachelor project 7 september 2011 56

Voorbeelden recente simulatiestudies (Alle voorbeelden hieronder zijn afstudeerstages bij Systeemkunde 2010 -2011) • • • • Verbeteren bagagesysteem E-kelder Schiphol Plaatsing nieuwe remises voor trams bij de HTM Doorrekenen logistiek nieuw schip voor pijpenleggen Heerema Simulatie voor risicomanagement Heerema Visualisatie en simulatie kosten gebruik van opvouwbare containers Gedistribueerde simulatie en serious games voor Pro. Rail Simulaties voor kadeprocessen Maersk containerterminal Rotterdam Doorrekenen wachtlijstproblematiek bij Jeugdzorg Verbeteren doorlooptijd laboratorium Reinier de Graaf ziekenhuis Verbeteren laad- en losprocessen Norfolkline terminal Vlaardingen Personeelsdoorstroming verbeteren bij grote organisaties (Accenture) Verbeteren voorraadposities bij Proctor & Gamble Pet Food Just-in-Time voorraadstrategie voor KLM motorenonderhoud Verbeteren prestaties fabricagelijn Ford in Engeland 7 september 2011 57

Opdracht 3 e en 4 e uur (v/a 10: 45) • Vorm groepen van 5 studenten • TBM vleugel “D” Logistieke problemen • kleine opgave • theoretische berekening • handsimulatie met dobbelstenen • Arena model • simulatie Schiphol grensfilter met Arena • simulatie Eiffeltoren met Arena • 1 computer per groep • 1 antwoordblad per groep inleveren 7 september 2011 58