TaskSpecific Information Amit Ashok 1 Pawan K Baheti

Task-Specific Information Amit Ashok 1, Pawan K Baheti 1 and Mark A. Neifeld 1, 2 Optical Computing and Processing Laboratory 1 Dept. of Electrical and Computer Engineering, 2 College of Optical Sciences, University of Arizona, Tucson. ece FIO/LS 2006

Presentation Outline • Images and Information • Task-specific information (TSI) • Detection and Localization tasks • Comparison for conventional and compressive imagers • Results and Conclusions ece FIO/LS 2006

Information content of an image 64 512 × 3 × 8 512 64 64 × 1 × 8 = 32 Kb = 6. 2 Mb Compression 512 24 Kb 2. 1 Mb • More precise measure requires source probability density ρ • • PROBLEM: ρ is very complex/unknown ece FIO/LS 2006

Motivation • Information content is task specific Detection task: For equal probability of presence/absence the information content < 1 bit Detection & Localization task: Probability of tank being absent = ½ ; Probability of occurrence in each region: ⅛ Information content < 2 bits Classification task: For equal probability of each target the information content < 1 bit • How to quantify task specific information (TSI) ece FIO/LS 2006

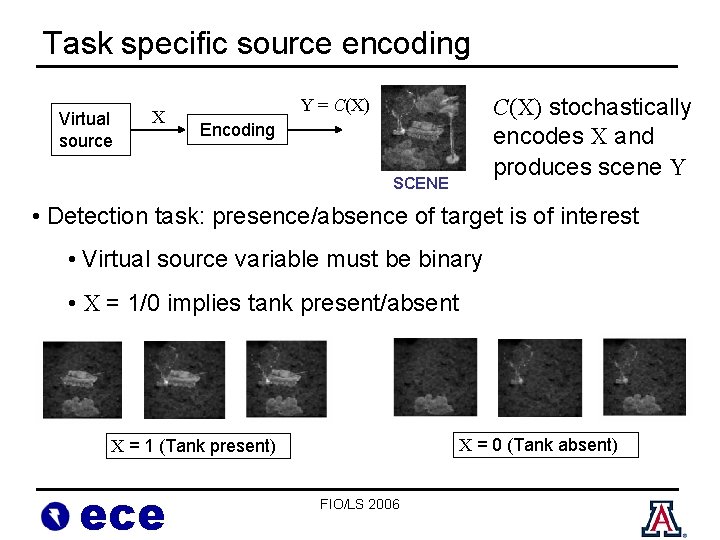
Task specific source encoding Virtual source X C(X) stochastically encodes X and produces scene Y Y = C(X) Encoding SCENE • Detection task: presence/absence of target is of interest • Virtual source variable must be binary • X = 1/0 implies tank present/absent X = 0 (Tank absent) X = 1 (Tank present) ece FIO/LS 2006

Task specific information (TSI) • Imaging chain block diagram Virtual source X Encoding Y = C(X) Channel SCENE H(Y) Noise R = n(H(C(X))) IMAGER • Imager is characterized by channel H and noise n • Imager does not add entropy to the relevant task • Definition for Task-specific information: Mutual information between X and R Always bounded by the entropy of X Entropy Z(X) – maximum task-specific information content ece FIO/LS 2006

TSI (continued) • Measurement can be written as n and s denote additive Gaussian noise and snr respectively • Computing TSI is difficult for non-Gaussian source • Use Verdu’s relation between mutual information and minimum estimation error ece FIO/LS 2006

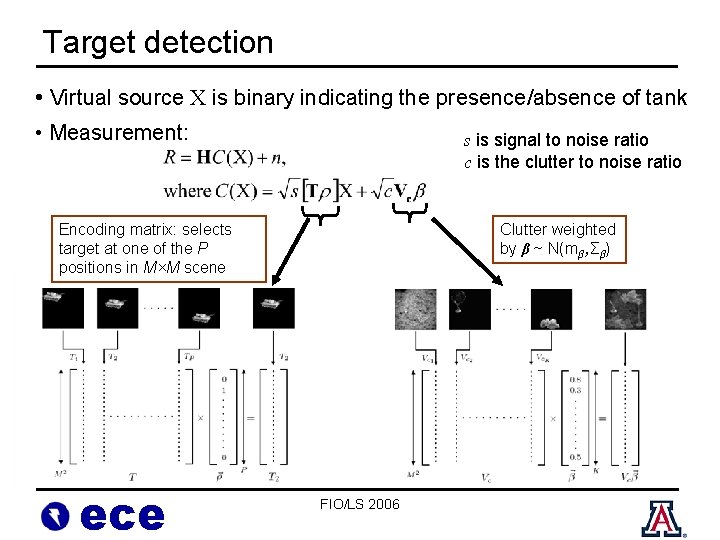
Target detection • Virtual source X is binary indicating the presence/absence of tank • Measurement: s is signal to noise ratio c is the clutter to noise ratio Encoding matrix: selects target at one of the P positions in M×M scene ece Clutter weighted by β ~ N(mβ , Σβ) FIO/LS 2006

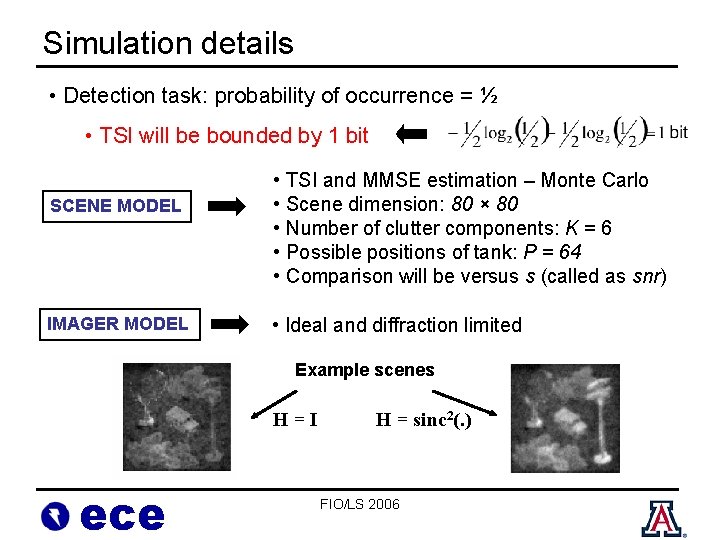
Simulation details • Detection task: probability of occurrence = ½ • TSI will be bounded by 1 bit SCENE MODEL IMAGER MODEL • TSI and MMSE estimation – Monte Carlo • Scene dimension: 80 × 80 • Number of clutter components: K = 6 • Possible positions of tank: P = 64 • Comparison will be versus s (called as snr) • Ideal and diffraction limited Example scenes H=I ece H = sinc 2(. ) FIO/LS 2006

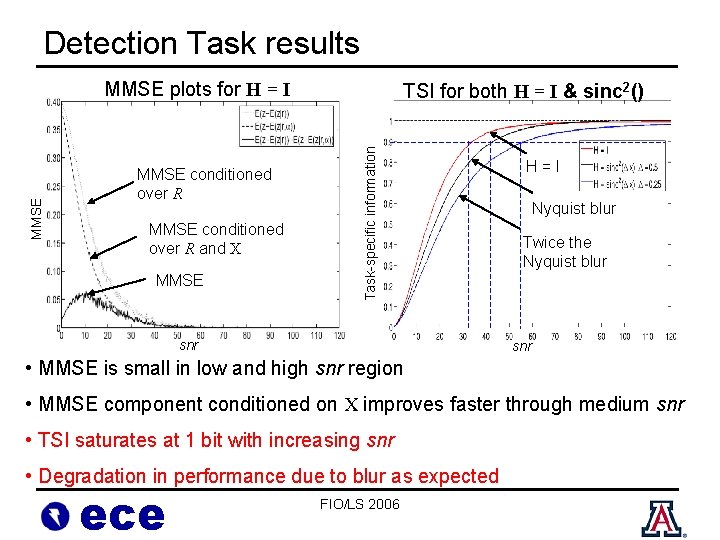
Detection Task results MMSE conditioned over R and X MMSE TSI for both H = I & sinc 2() Task-specific information MMSE plots for H = I snr H=I Nyquist blur Twice the Nyquist blur snr • MMSE is small in low and high snr region • MMSE component conditioned on X improves faster through medium snr • TSI saturates at 1 bit with increasing snr • Degradation in performance due to blur as expected ece FIO/LS 2006

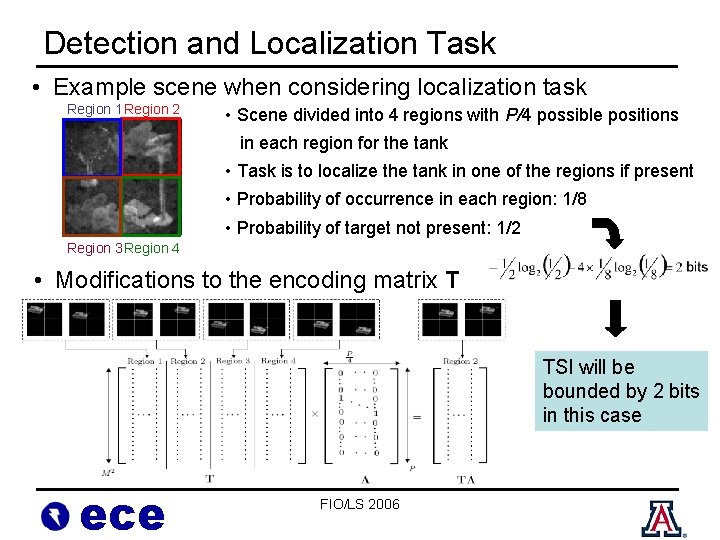
Detection and Localization Task • Example scene when considering localization task Region 1 Region 2 • Scene divided into 4 regions with P/4 possible positions in each region for the tank • Task is to localize the tank in one of the regions if present • Probability of occurrence in each region: 1/8 • Probability of target not present: 1/2 Region 3 Region 4 • Modifications to the encoding matrix T TSI will be bounded by 2 bits in this case ece FIO/LS 2006

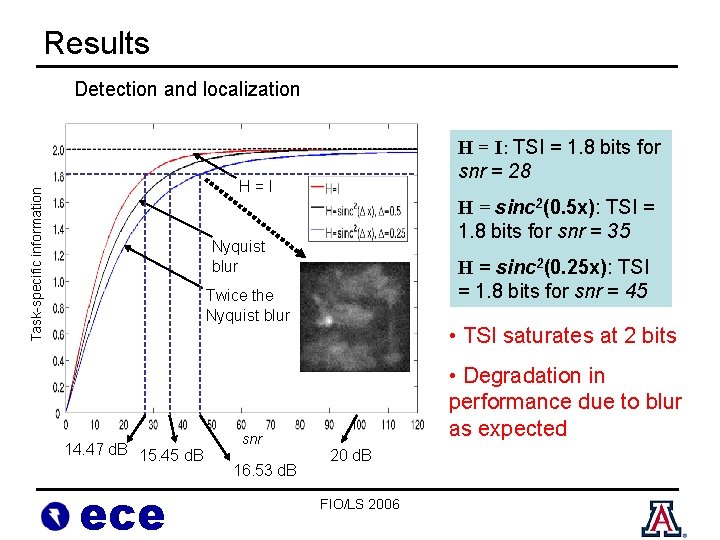
Results Detection and localization H = I: TSI = 1. 8 bits for snr = 28 Task-specific information H=I H = sinc 2(0. 5 x): TSI = 1. 8 bits for snr = 35 Nyquist blur H = sinc 2(0. 25 x): TSI = 1. 8 bits for snr = 45 Twice the Nyquist blur 14. 47 d. B 15. 45 d. B ece snr 16. 53 d. B • TSI saturates at 2 bits • Degradation in performance due to blur as expected 20 d. B FIO/LS 2006

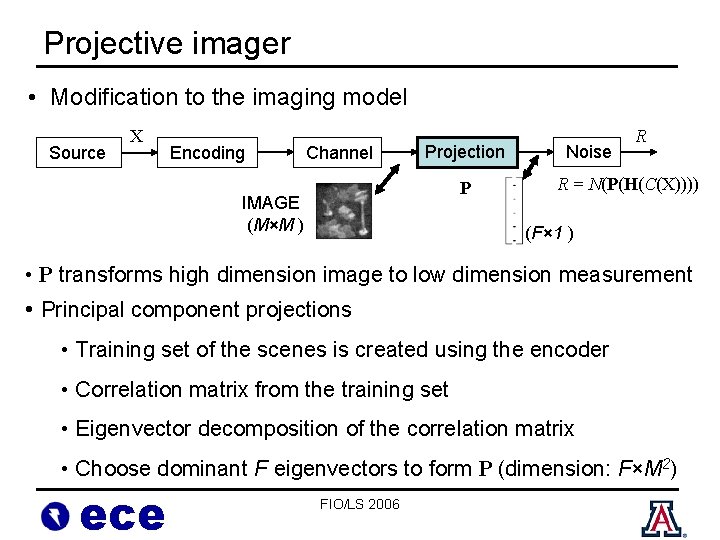
Projective imager • Modification to the imaging model Source X Encoding Channel Projection P IMAGE (M×M ) Noise R R = N(P(H(C(X)))) (F× 1 ) • P transforms high dimension image to low dimension measurement • Principal component projections • Training set of the scenes is created using the encoder • Correlation matrix from the training set • Eigenvector decomposition of the correlation matrix • Choose dominant F eigenvectors to form P (dimension: F×M 2) ece FIO/LS 2006

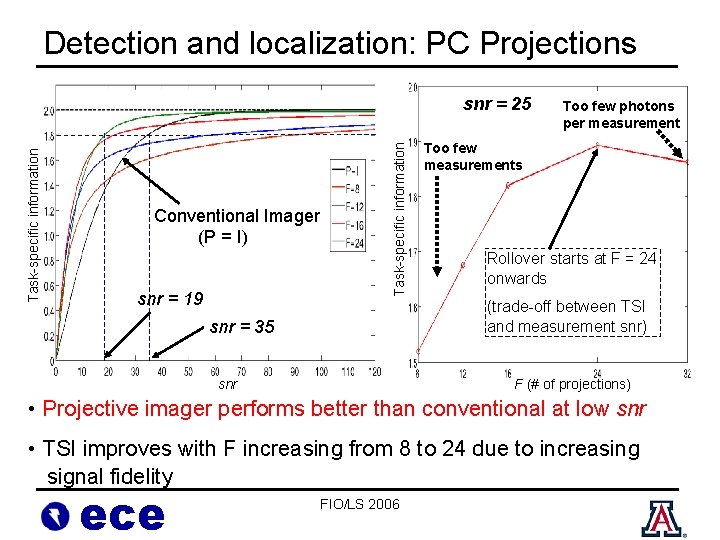
Detection and localization: PC Projections Conventional Imager (P = I) snr = 19 Task-specific information snr = 25 Too few photons per measurement Too few measurements Rollover starts at F = 24 onwards (trade-off between TSI and measurement snr) snr = 35 snr F (# of projections) • Projective imager performs better than conventional at low snr • TSI improves with F increasing from 8 to 24 due to increasing signal fidelity ece FIO/LS 2006

Conclusions • Information content of an image is associated with a task • Introduced the framework for task-specific information • TSI confirms our intuition about ideal, diffraction-limited and projective imagers • Can be used as a metric to optimize the systems based on task specificity ece FIO/LS 2006