Tangents and Gradients Points with a Given Gradient






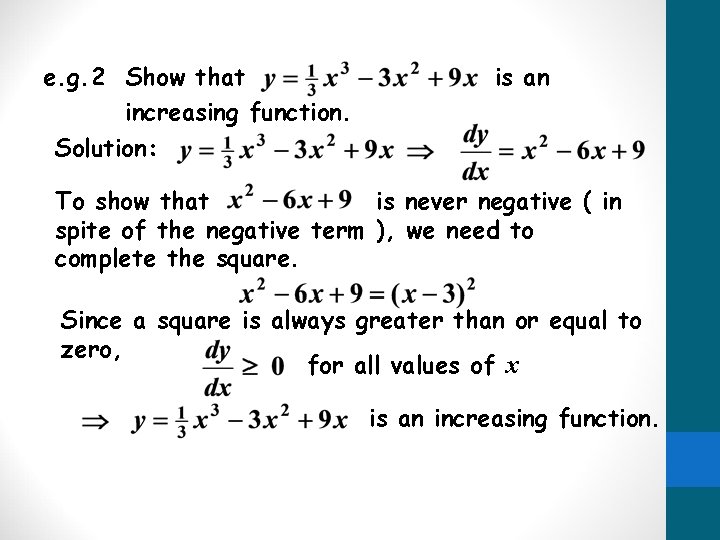








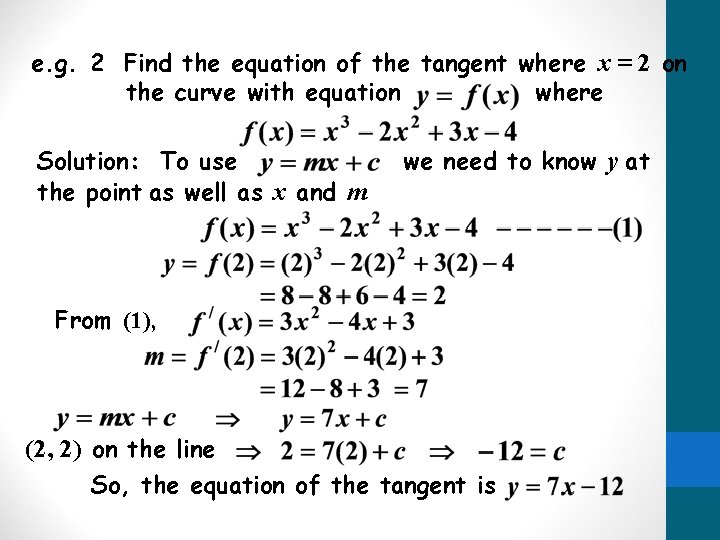
- Slides: 20

Tangents and Gradients

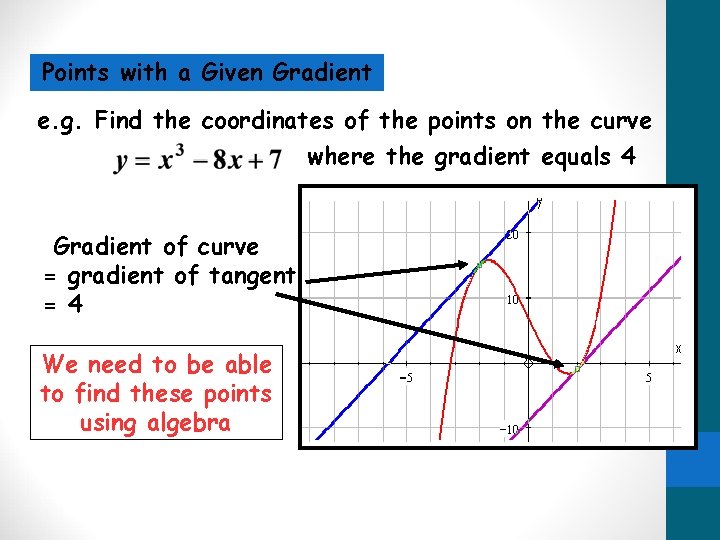
Points with a Given Gradient e. g. Find the coordinates of the points on the curve where the gradient equals 4 Gradient of curve = gradient of tangent = 4 We need to be able to find these points using algebra

Points with a Given Gradient e. g. Find the coordinates of the points on the curve where the gradient is 4 Solution: The gradient of the curve is given by Gradient is 4 Quadratic equation with no linear x -term

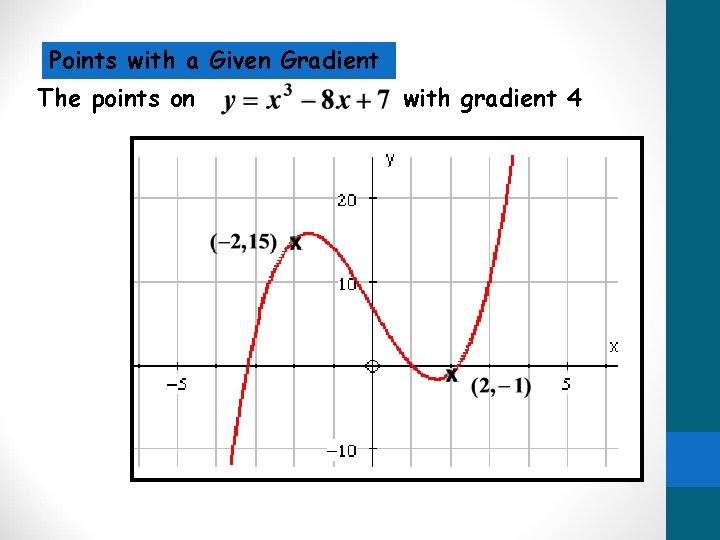
Points with a Given Gradient The points on with gradient 4

SUMMARY Ø To find the point(s) on a curve given gradient: • find the gradient function • let • solve the resulting equation equal the given gradient with a

Exercises Find the coordinates of the points on the curves with the gradients given 1. where the gradient is -2 Ans: (-3, -6) 2. where the gradient is 3 ( Watch out for the common factor in the quadratic equation ) Ans: (-2, 2) and (4, -88)

Increasing and Decreasing Functions • An increasing function is one whose gradient is always greater than or equal to zero. for all values of x • A decreasing function has a gradient that is always negative or zero. for all values of x

e. g. 1 Show that function Solution: is an increasing is the sum of • a positive number ( 3 ) a perfect square ( which is positive or zero for all values of x, and • a positive number ( 4 ) for all values of x so, is an increasing function
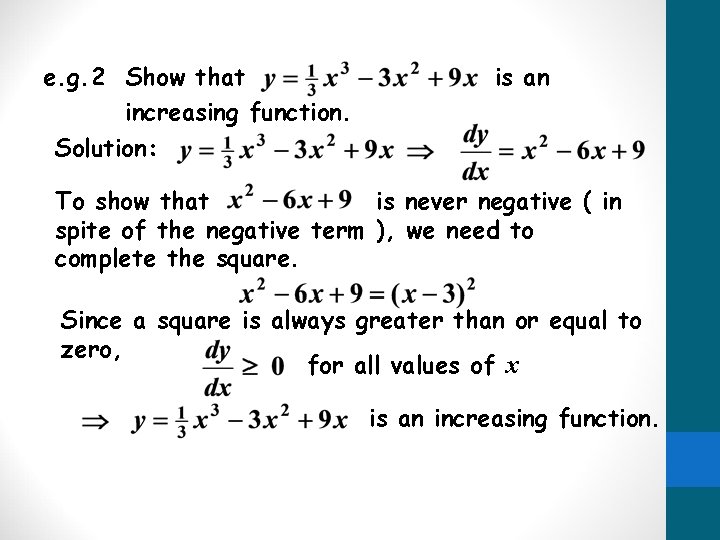
e. g. 2 Show that increasing function. Solution: is an To show that is never negative ( in spite of the negative term ), we need to complete the square. Since a square is always greater than or equal to zero, for all values of x is an increasing function.

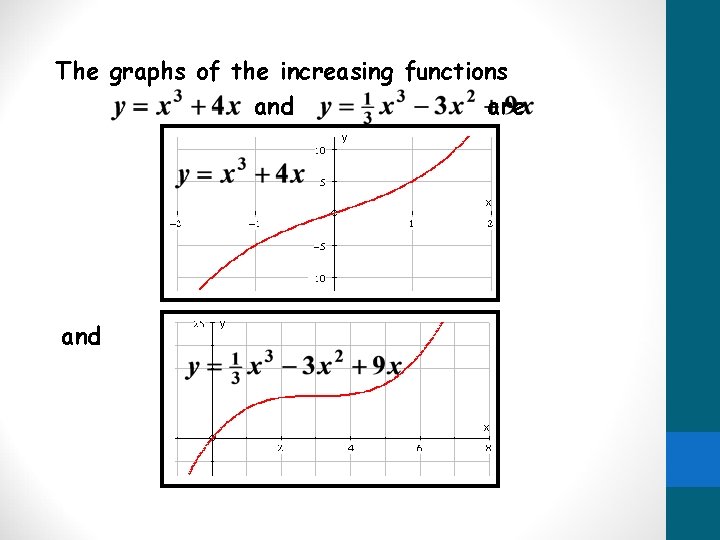
The graphs of the increasing functions and are and

Exercises 1. Show that sketch its graph. is a decreasing function and 2. Show that function and sketch its graph. is an increasing Solutions are on the next 2 slides.

Solutions 1. Show that sketch its graph. Solution: is a decreasing function and. This is the product of a square which is always so for all x. Hence decreasing function. and a negative number, is a

Solutions 2. Show that function and sketch its graph. Solution: is an increasing . Completing the square: which is the sum of a square which is and a positive number. Hence y is an increasing function.

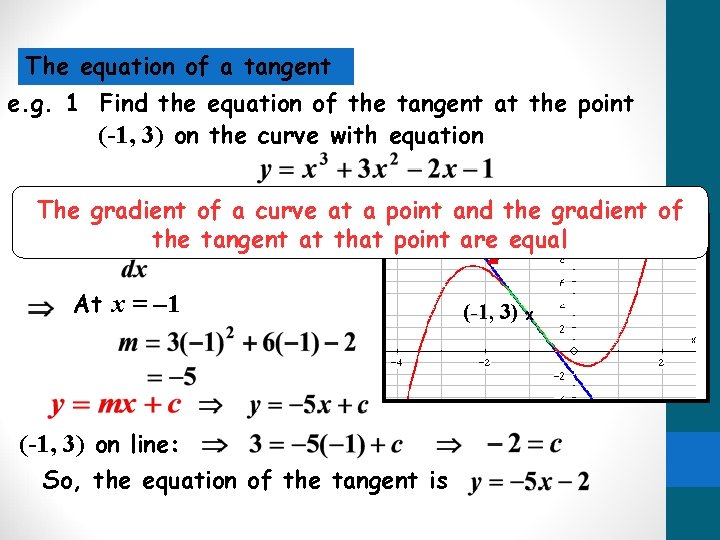
The equation of a tangent e. g. 1 Find the equation of the tangent at the point (-1, 3) on the curve with equation Solution: The gradient of a curve at a point and the gradient of Gradient -5 the tangent at that point are =equal At x = -1 (-1, 3) on line: So, the equation of the tangent is (-1, 3) x

An Alternative Notation The notation for a function of x can be used instead of y. When is used, instead of using for the gradient function, we write ( We read this as “ f dashed x ” ) This notation is helpful if we need to substitute for x. e. g.

e. g. 2 Find the equation of the tangent where x = 2 on the curve with equation where Solution: To use the point as well as x and m we need to know y at From (1), (2, 2) on the line So, the equation of the tangent is

SUMMARY Ø To find the equation of the tangent at a point on the curve : • if the y-value at the point is not given, substitute the x -value into the equation of the curve to find y • find the gradient function • substitute the x-value into to find the gradient of the tangent, m • substitute for y, m and x into to find c

Exercises 1. Find the equation of the tangent to the curve at the point (2, -1) Ans: 2. Find the equation of the tangent to the curve at the point x = -1, where Ans:

The equation of a tangent e. g. 1 Find the equation of the tangent at the point (-1, 3) on the curve with equation Solution: Gradient = -5 At x = -1 (-1, 3) on line: So, the equation of the tangent is (-1, 3) x
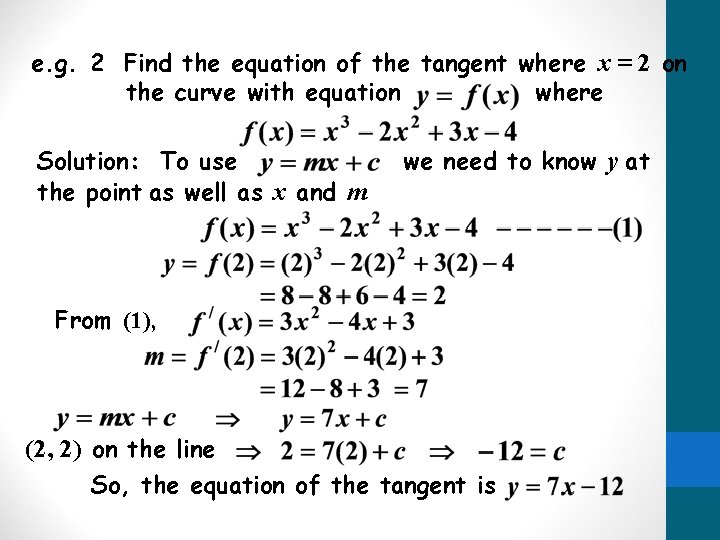
e. g. 2 Find the equation of the tangent where x = 2 on the curve with equation where Solution: To use the point as well as x and m we need to know y at From (1), (2, 2) on the line So, the equation of the tangent is