TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute Bioelectromagnetism

TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute Bioelectromagnetism Exercise #3 – Answers

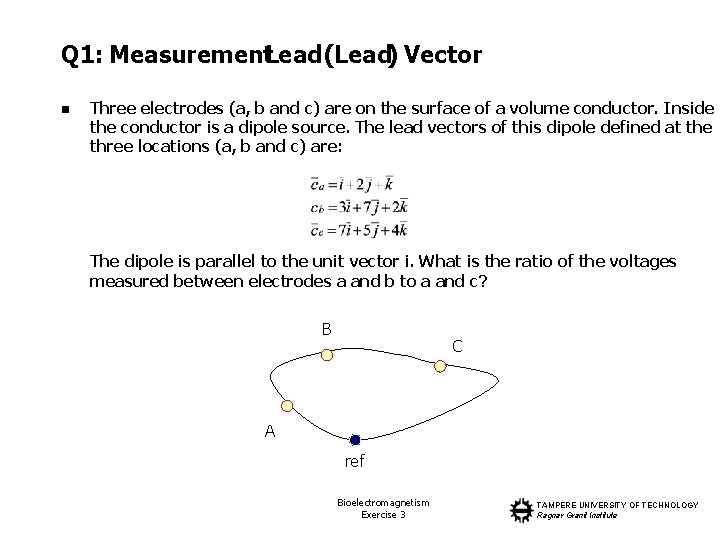
Q 1: Measurement. Lead (Lead) Vector n Three electrodes (a, b and c) are on the surface of a volume conductor. Inside the conductor is a dipole source. The lead vectors of this dipole defined at the three locations (a, b and c) are: The dipole is parallel to the unit vector i. What is the ratio of the voltages measured between electrodes a and b to a and c? B C A ref Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

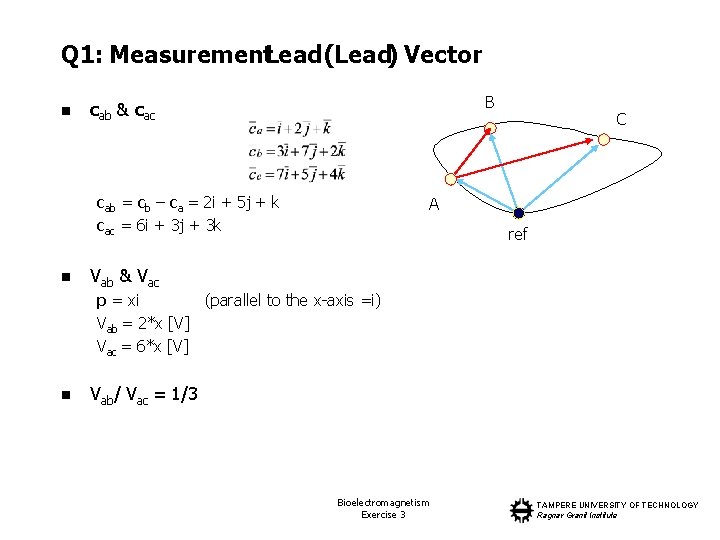
Q 1: Measurement. Lead (Lead) Vector n B cab & cac cab = cb – ca = 2 i + 5 j + k cac = 6 i + 3 j + 3 k n C A ref Vab & Vac p = xi (parallel to the x-axis =i) Vab = 2*x [V] Vac = 6*x [V] n Vab/ Vac = 1/3 Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

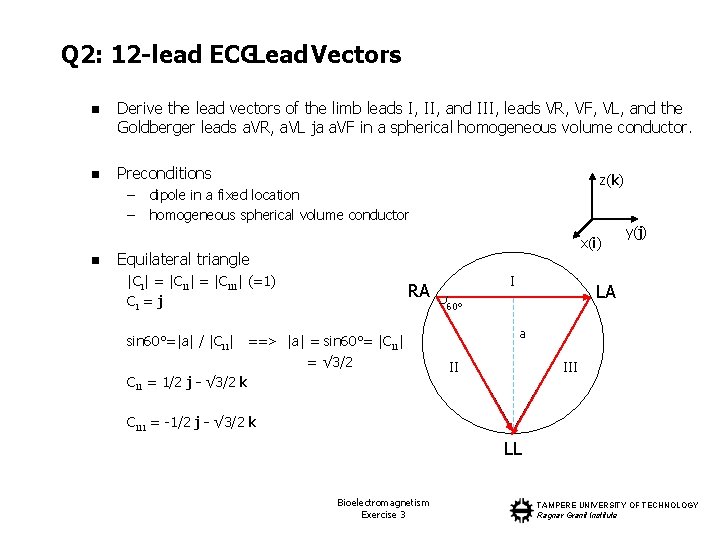
Q 2: 12 -lead ECGLead Vectors n Derive the lead vectors of the limb leads I, II, and III, leads VR, VF, VL, and the Goldberger leads a. VR, a. VL ja a. VF in a spherical homogeneous volume conductor. n Preconditions – – n z(k) dipole in a fixed location homogeneous spherical volume conductor x(i) Equilateral triangle |CI| = |CIII| (=1) CI = j RA sin 60°=|a| / |CII| ==> |a| = sin 60°= |CII| = √ 3/2 CII = 1/2 j - √ 3/2 k I y(j) LA 60° a II III CIII = -1/2 j - √ 3/2 k LL Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

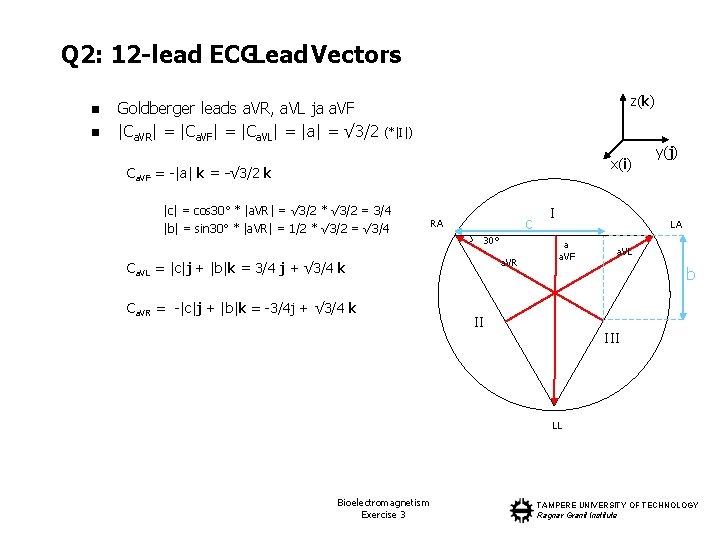
Q 2: 12 -lead ECGLead Vectors n n Goldberger leads a. VR, a. VL ja a. VF |Ca. VR| = |Ca. VF| = |Ca. VL| = |a| = √ 3/2 z(k) (*|I|) x(i) Ca. VF = -|a| k = -√ 3/2 k |c| = cos 30° * |a. VR| = √ 3/2 * √ 3/2 = 3/4 |b| = sin 30° * |a. VR| = 1/2 * √ 3/2 = √ 3/4 c RA 30° a. VR Ca. VL = |c|j + |b|k = 3/4 j + √ 3/4 k Ca. VR = -|c|j + |b|k = -3/4 j + √ 3/4 k I y(j) LA a a. VF a. VL b II III LL Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

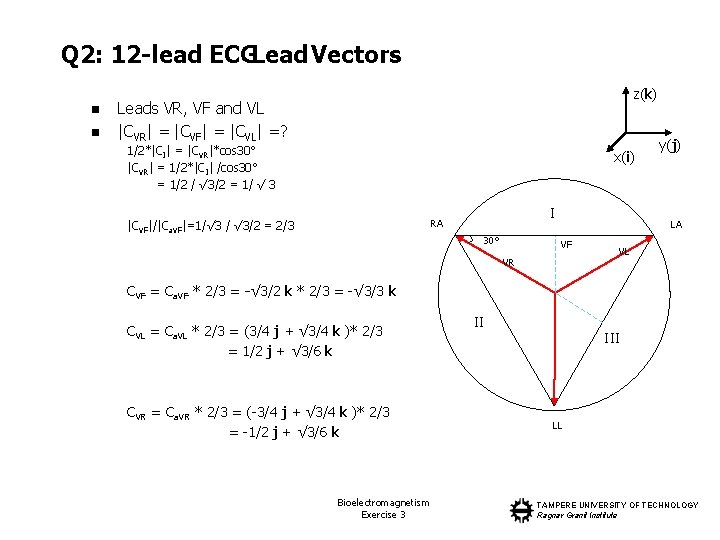
Q 2: 12 -lead ECGLead Vectors n n z(k) Leads VR, VF and VL |CVR| = |CVF| = |CVL| =? 1/2*|CI| = |CVR|*cos 30° |CVR| = 1/2*|CI| /cos 30° = 1/2 / √ 3/2 = 1/ √ 3 x(i) I RA |CVF|/|Ca. VF|=1/√ 3 / √ 3/2 = 2/3 30° y(j) LA VF VR VL CVF = Ca. VF * 2/3 = -√ 3/2 k * 2/3 = -√ 3/3 k CVL = Ca. VL * 2/3 = (3/4 j + √ 3/4 k )* 2/3 = 1/2 j + √ 3/6 k CVR = Ca. VR * 2/3 = (-3/4 j + √ 3/4 k )* 2/3 = -1/2 j + √ 3/6 k Bioelectromagnetism Exercise 3 II III LL TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

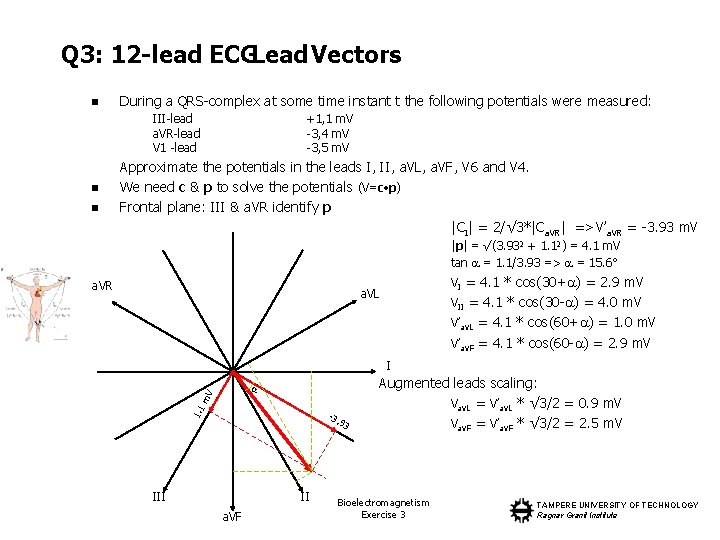
Q 3: 12 -lead ECGLead Vectors n During a QRS-complex at some time instant t the following potentials were measured: III-lead a. VR-lead V 1 -lead n n +1, 1 m. V -3, 4 m. V -3, 5 m. V Approximate the potentials in the leads I, II, a. VL, a. VF, V 6 and V 4. We need c & p to solve the potentials (V=c • p) Frontal plane: III & a. VR identify p |CI| = 2/√ 3*|Ca. VR| =>V’a. VR = -3. 93 m. V |p| = √(3. 932 + 1. 12) = 4. 1 m. V tan = 1. 1/3. 93 => = 15. 6° a. VR VI = 4. 1 * cos(30+ ) = 2. 9 m. V a. VL VII = 4. 1 * cos(30 - ) = 4. 0 m. V V’a. VL = 4. 1 * cos(60+ ) = 1. 0 m. V V’a. VF = 4. 1 * cos(60 - ) = 2. 9 m. V I 1. 1 m. V -3. 93 III II a. VF Augmented leads scaling: Va. VL = V’a. VL * √ 3/2 = 0. 9 m. V Va. VF = V’a. VF * √ 3/2 = 2. 5 m. V Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

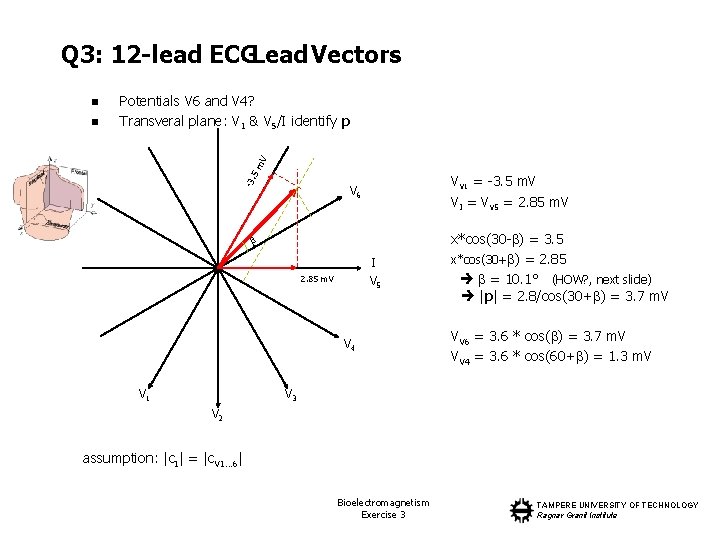
Q 3: 12 -lead ECGLead Vectors n -3. 5 m V n Potentials V 6 and V 4? Transveral plane: V 1 & V 5/I identify p VV 1 = -3. 5 m. V VI = VV 5 = 2. 85 m. V V 6 I 2. 85 m. V V 5 V 4 V 1 x*cos(30 - ) = 3. 5 x*cos(30+ ) = 2. 85 = 10. 1° (HOW? , next slide) |p| = 2. 8/cos(30+ ) = 3. 7 m. V VV 6 = 3. 6 * cos( ) = 3. 7 m. V VV 4 = 3. 6 * cos(60+ ) = 1. 3 m. V V 3 V 2 assumption: |c. I| = |c. V 1… 6| Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

Q 3: 12 -lead ECGLead Vectors Summation equation: cos(x y) = cosxcosy sinxsiny x*cos(30 - ) = 3. 5 => cos 30 cos + sin 30 sin = 3. 5/X x*cos(30+ ) = 2. 85 => x = 2. 85/(cos 30 cos -sin 30 sin ) cos 30 cos + sin 30 sin = 3. 5/ 2. 85 * (cos 30 cos -sin 30 sin ) cos 30 cos -1. 25*cos 30 cos = -a*sin 30 sin - sin 30 sin (a=3. 5/2. 85) (cos 30 -a*cos 30)*cos = -(a*sin 30+sin 30)*sin /cos = -(cos 30 -a*cos 30)/(a*sin 30+sin 30) tan = 0. 1755 => =10. 1° Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

Q 4: Lead vectors… n On the outer rim of a two dimensional volume conductor at points P i, i = 1, . . . , 6 the potentials generated by a unit dipole oriented parallel to X or Y axes at point Po are as follows: Electrode Pi 1 2 3 4 5 6 n Potentials generated by X and Y dipoles VX VY 4 6 1 -4 -4 -1 5 -1 -4 -2 2 5 Using these measurements is it possible to a) Derive the image surface of this source dipole location? b) Calculate the lead vector of a lead between the points 3 and 6? c) Derive the potential at the point 4 generated by a unit dipole at a point Pz? d) Derive the lead field of the volume conductor? e) Construct a VECG lead system (X and Y-leads) that would measure the X and Y components of the dipole at the point Po with similar sensitivity? Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

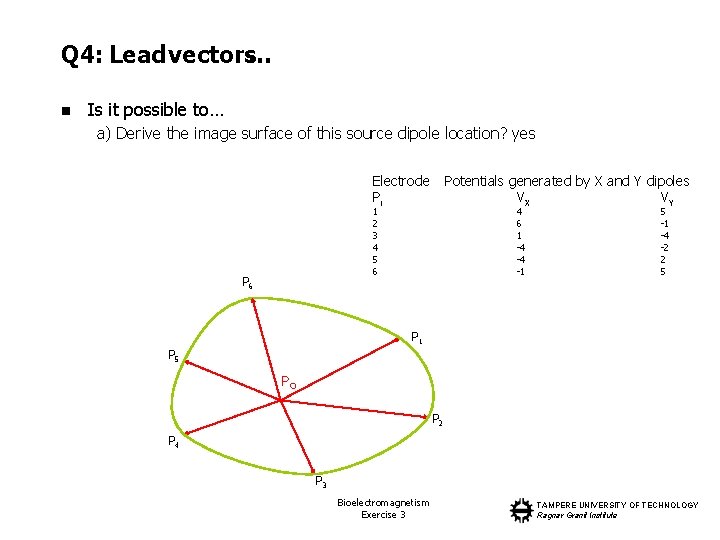
Q 4: Lead vectors… n Is it possible to… a) Derive the image surface of this source dipole location? yes Electrode Pi Potentials generated by X and Y dipoles VX VY 1 2 3 4 5 6 P 6 4 6 1 -4 -4 -1 5 -1 -4 -2 2 5 P 1 P 5 PO P 2 P 4 P 3 Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

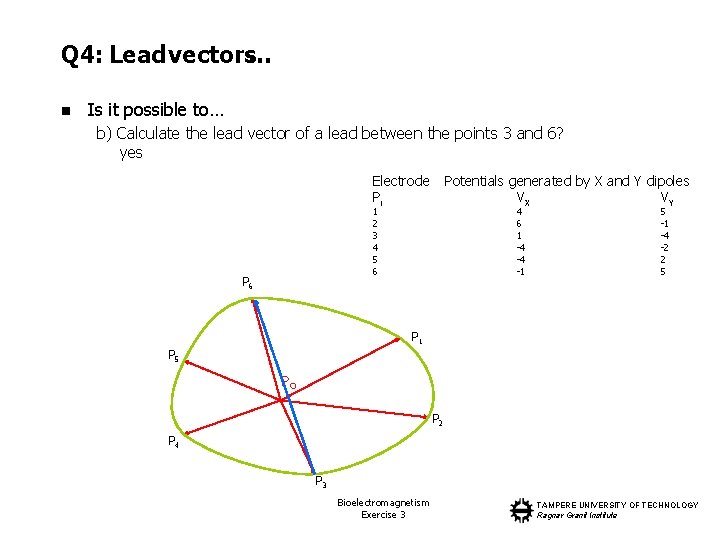
Q 4: Lead vectors… n Is it possible to… b) Calculate the lead vector of a lead between the points 3 and 6? yes Electrode Pi Potentials generated by X and Y dipoles VX VY 1 2 3 4 5 6 P 6 4 6 1 -4 -4 -1 5 -1 -4 -2 2 5 P 1 P 5 PO P 2 P 4 P 3 Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

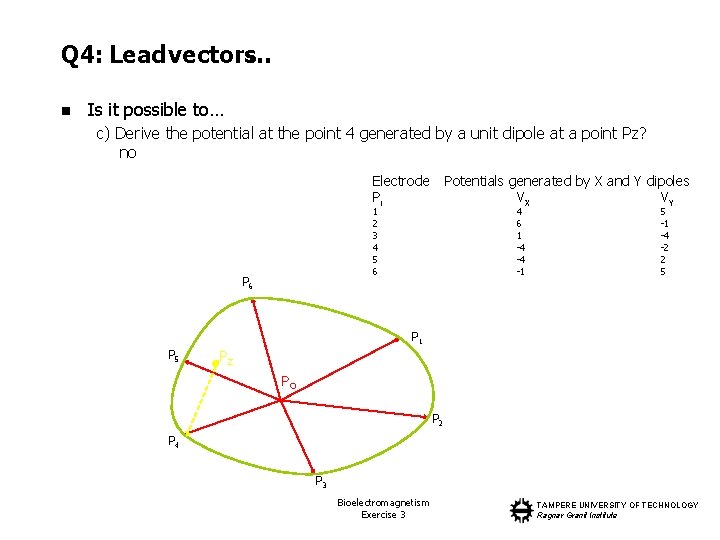
Q 4: Lead vectors… n Is it possible to… c) Derive the potential at the point 4 generated by a unit dipole at a point Pz? no Electrode Pi Potentials generated by X and Y dipoles VX VY 1 2 3 4 5 6 P 6 4 6 1 -4 -4 -1 5 -1 -4 -2 2 5 P 1 P 5 PZ PO P 2 P 4 P 3 Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

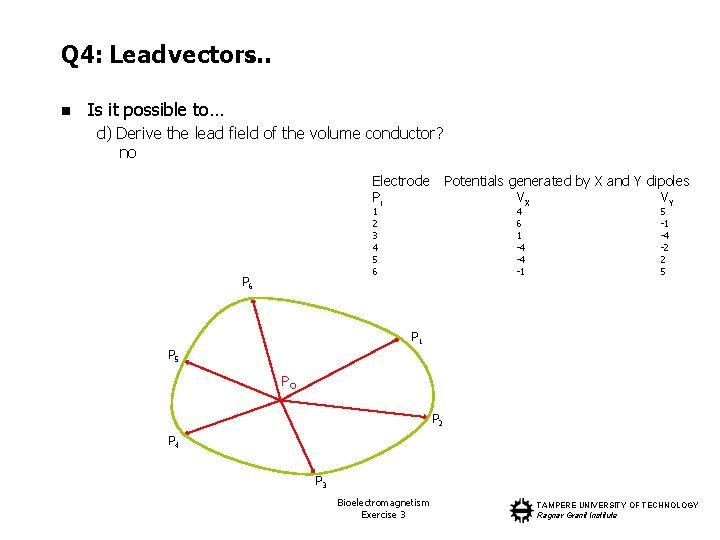
Q 4: Lead vectors… n Is it possible to… d) Derive the lead field of the volume conductor? no Electrode Pi Potentials generated by X and Y dipoles VX VY 1 2 3 4 5 6 P 6 4 6 1 -4 -4 -1 5 -1 -4 -2 2 5 P 1 P 5 PO P 2 P 4 P 3 Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

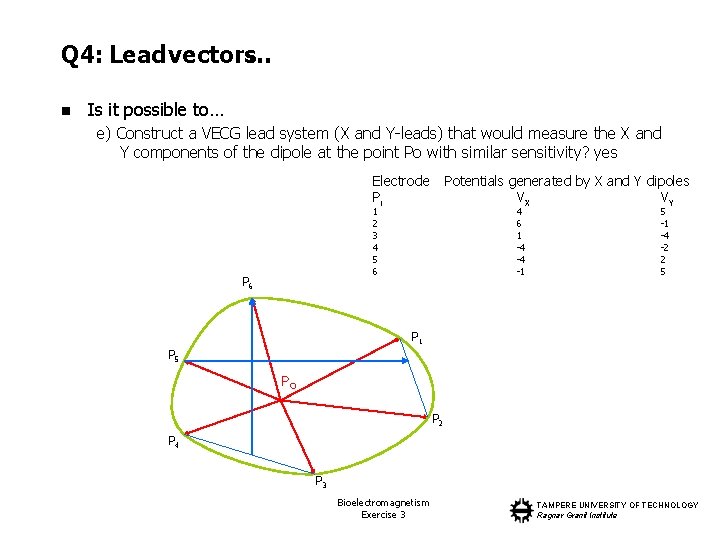
Q 4: Lead vectors… n Is it possible to… e) Construct a VECG lead system (X and Y-leads) that would measure the X and Y components of the dipole at the point Po with similar sensitivity? yes Electrode Pi Potentials generated by X and Y dipoles VX VY 1 2 3 4 5 6 P 6 4 6 1 -4 -4 -1 5 -1 -4 -2 2 5 P 1 P 5 PO P 2 P 4 P 3 Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

Q 5: EEG Sensitivity n Figure 1 represents a potential data distribution at a model of a (half) head generated by a reciprocal current of 1. 0 µA applied to electrodes C and D. Calculate the potential between electrodes C and D generated by current dipoles A and B (|P| = 4 µAcm). Fig 1. Potential data at surface of a electrolytic tank (midsagittal plane). Lines between 0. 1 m. V curves are spaced at equal potential differences (0. 02 m. V) apart. I=1. 0 µA in the half-head model; fluid Bioelectromagnetism TAMPERE UNIVERSITY OF TECHNOLOGY resistivity is 2220 Ωcm. Exercise 3 Ragnar Granit Institute

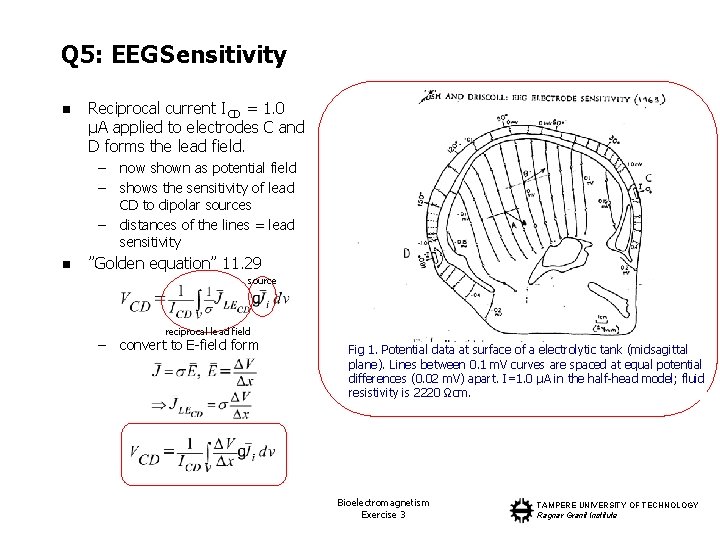
Q 5: EEG Sensitivity n Reciprocal current ICD = 1. 0 µA applied to electrodes C and D forms the lead field. – – – n now shown as potential field shows the sensitivity of lead CD to dipolar sources distances of the lines = lead sensitivity ”Golden equation” 11. 29 source – reciprocal lead field convert to E-field form Fig 1. Potential data at surface of a electrolytic tank (midsagittal plane). Lines between 0. 1 m. V curves are spaced at equal potential differences (0. 02 m. V) apart. I=1. 0 µA in the half-head model; fluid resistivity is 2220 Ωcm. Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute

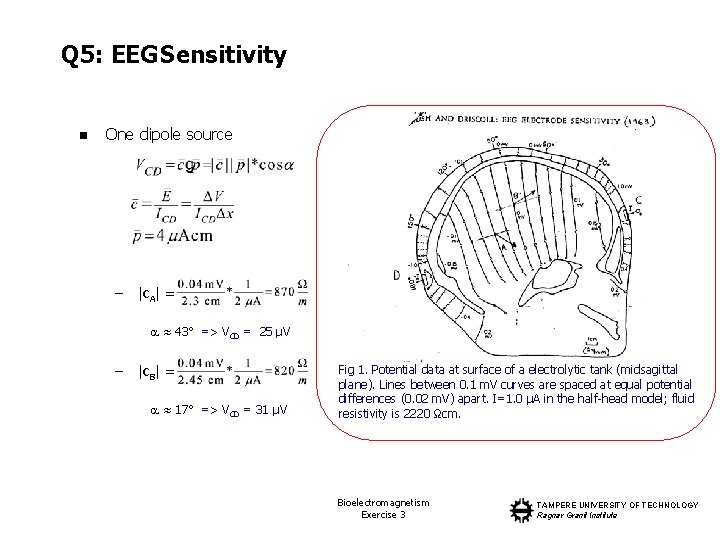
Q 5: EEG Sensitivity n One dipole source – |c. A| = ≈ 43° => VCD = 25 µV – |c. B| = ≈ 17° => VCD = 31 µV Fig 1. Potential data at surface of a electrolytic tank (midsagittal plane). Lines between 0. 1 m. V curves are spaced at equal potential differences (0. 02 m. V) apart. I=1. 0 µA in the half-head model; fluid resistivity is 2220 Ωcm. Bioelectromagnetism Exercise 3 TAMPERE UNIVERSITY OF TECHNOLOGY Ragnar Granit Institute