Talking Statistics Impressions from the ATLAS Statistics WS

Talking Statistics Impressions from the ATLAS Statistics WS, Jan 2007 Andreas Hoecker (CERN) CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 1

Preliminary Remarks Main statistical topics of importance for HEP data analysis Avoid biases (statistics is science – its correct use is not a question of taste !) Be objective: use frequentist statistics as much as possible Determine statistical approach beforehand “Gauge” your test statistics with toy Monte Carlo experiments Be “blind” during analysis optimisation and systematics studies Choose optimised approaches (under all aspects, i. e. , including systematics) Use multivariate techniques (minimise Type-II errors) Minimise Type-I errors Precisely model your data Optimise your test statistics (include all available information) CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 2

Preliminaries CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 3

Significance p-value: P (data reject H 0|H 0), where H 0 null hypothesis G. Cowan, Introduction Probability of getting a value of test statistic more signal-like than that observed, if the null hypothesis is true In frequentist statistics one cannot talk about P (H 0), unless H 0 is a repeatable observation The p-value is equal to the significance level of the test for which we would only reject the null hypothesis. The p-value is compared with the significance level and, if it is smaller, the result is significant. Define beforehand what leads to an exclusion of the null hypothesis One-sided p-value: e. g. , only N > N [H 0] leads to exclusion Two-sided p-value: e. g. , any deviation from N [H 0] leads to exclusion For Gaussian test statistics: pone-sided = 0. 5×ptwo-sided CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 4

Kinds of Errors in Statistical Interpretation Type-I error: reject null hypothesis though it is true G. Cowan, Introduction S. Caron, Search strategies … Frequency of Type-I errors rises with number of trials Naïve p-value must be corrected: for n independent trials: pcorr = 1– (1 – p)n “Look elsewhere effect” Frequency of Type-I errors independent of analysis optimisation (unless prior information can be exploited) Type-II error: accept null hypothesis though it is not true The frequency of Type-II errors depends on analysis optimisation It may decrease with number of trials Goal: minimise frequency of Type-I and Type-II errors Focus search using prior information (e. g. , SUSY may have large ET, miss) Optimise the sensitivity of the analysis using prior information CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 5

Frequentist versus Subjective (Bayesian) Frequentist probability defines an event's probability as the limit of its relative frequency in a large number of trials G. Cowan, Introduction The true outcome of an event is fixed but not known and cannot be known The tools of frequentist statistics tell us what to expect, under the assumption of certain probabilities, about hypothetical repeated observations Frequentist confidence levels (CLs) are straightforwardly obtained from toy MC samples The nuisance parameters in these toys must be set such that the lowest CLs are obtained Confidence levels determine exclusion probabilities. If in presence of nuisance parameters a measurement gave x ± , this does not mean that x is the most probable value ! Subjective Bayesian statistics gives the probability of x to take some value It is the result of a convolution of input PDFs for all observables and nuisance parameters The “posterior” result is subjective w. r. t. the arbitrary prior PDFs, bounds and parameterisations used It is extremely difficult to reproduce a Bayesian result w/o having all the subjective details CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 6

A Frequentist Analysis The principles of a frequentist analysis are simple: G. Cowan, Introduction Define a test statistics, e. g. : a Likelihood estimator a multivariate analyser output Your age Throw toy experiments and determine the p-value to achieve an as extreme or more extreme value than the one found in the data Examples: exclusion analysis, Nobs events observed for Nexp expected: determine the fraction of toy experiments with null hypothesis for which Nobs Nexp measurement, x 0 ± : throw toys with true value x 0 – , and determine fraction of experiments with x 0, toy x 0, same for positive error If one wants to be smart, one can compute the first example by hand: That’s elegant, but there is no law that requires elegance… CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 7

More Complicated When the model gets more realistic, elegant solutions are not always straightforward… T. Eifert-AH Examples: exclusion analysis, Nobs events observed for Nexp expected – but: Nexp has uncertainty ! If one wants to be smart, one can computes the p-value by hand: 1 F 1 are confluent hypergeometric functions of first kind where: Is this any elegant ? toys perform numerical integration and are super simple, just use: TRandom: : Poisson(Nobs, N ) TRandom: : Gauss(N , Nexp, ) CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 8

Categorisation of Systematic Errors K. Cranmer Class - I: the Good Can be taken from auxiliary measurements Taken from P. Sinervo’s Phy. Stat 03 talk Well behaved statistics wise, improve with luminosity Class - II: the Bad Arise from poorly understood analysis features or model assumptions Can control size of effects No statistical meaning, may be modeled by Gaussians (giving it Bayesian credibility intervals) following “central limit theorem” Class - III: the Evil Arise from theoretical assumptions or uncontrolled model uncertainties Cannot reasonably control size of effect No statistical meaning, no reasonable prior modeling CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 9

A statistical method has “coverage” (1–α) if, in infinitely many repeated experiments the resulting CLs include (cover) the true value in a fraction (1–α) of all cases (irrespective of what the true value is) Coverage Treat the test statistics interpretation (limit setting procedure, errors) as black box K. Cranmer Fix its nuisance parameters (e. g. , to values found in a maximum-likelihood fit) Generate toy MC samples Determine the true Type-I error rate for this setup Compare with initial statistical interpretation: test its “coverage” Undercoverage “optimistic” Overcoverage “conservative” Best is good coverage Coverage calibrates the statistical apparatus Different statistical methods may have different coverage ! CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues Coverage versus nuisance parameters G. Punzi, Phy. Stat’ 05 10

Applications CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 11

Example: Higgs Searches at LEP A. Read, Lessons from LEP Higgs searches at LEP Likelihood includes shape information Test statistics likelihood ratio (LR): Determine PDFs for ln. Q with MC Other test statistics have been tried: similar sensitivity to exclusion and discovery, but none performed better Define another statistics “CLs” to obtain lower bound on m. H The P’s are obtained from integrating Q PDFs The CLs is not gauged with MC anymore, but directly used CLs(m. H) = 0. 05, m. H is excluded at 95% This interpretation leads to an overcoverage, i. e. , to a conservative (too low) limit Ouf ! (why so complicated ? ) CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 12

Example: Lessons from TEVATRON T. Junks, Lessons from Tevatron Tom Junk gave an interesting talk about lessons from Tevatron. Many concrete examples of statistics use cases and pitfalls (some touched in this résumé). Too rich to summarise here. Have a look yourself ! CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 13

Example: ATLAS Higgs Searches W. Quayle, Higgs searches “You can’t do discovery physics at LHC without at least a little bit of statistical analysis” … my god ! Use as straightforward statistical arguments (LEP missed that one), which are as rigorous as possible Points out danger of Type-I errors when scanning m. H range [Guillaume et al. ’s note, ‘ 06] Bill advertises to perform a fit of m. H instead [EPJ C 45, 659 (2006)] AH: cannot believe it makes a difference whether one scans or fits m. H Toy MC must model the entire hypothesis test ! “Many analyses evolve towards background extraction from ML fits” H (use categories in rapidity & more variables, fit nuisance parameters) tt. H (H bb) (fit m. H and signal, background yields) H WW qq (uncertainty in BG, signal can be near BG peak, W + jets control samples) + others … Combined limit/discovery: combine test statistics (e. g. , likelihoods) ? requires combined toy analysis ! Combine confidence levels ? not unambiguous ! Hot topic, I guess ! CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 14

Example: ATLAS SUSY Searches MSSM has 105 parameters use constrained models for signal MC (e. g. , m. SUGRA with 4. 5 parameters) T. Lari, Stat issues in SUSY searches Searches driven by signature: hard jets, LSP (ET, miss), large Meff, maybe leptons Optimise (and finalize) analysis before looking into signal region ! Statistics challenges: Optimise analysis at a single m. SUGRA point ? (small T-I error, but maybe large T-II error) Optimise and test full m. SUGRA grid ? (large T-I error, maybe smaller T-II error) Apply “general search strategy” (S. Caron) ? (huge T-I error, maybe smaller T-II error) We can compute rate of T-I errors, but do not know anything about the T-II error rate ! Optimisation should include systematics ! Other challenges, potentially more important for early discovery: Need to control backgrounds (from data ? ) and systematic errors Can we extrapolate background from “sidebands” into signal region ? CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 15

Analysis Optimisation CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 16

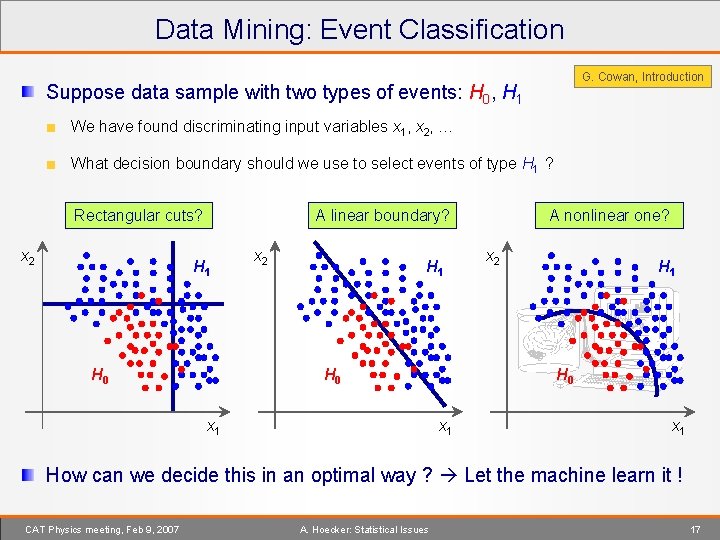
Data Mining: Event Classification G. Cowan, Introduction Suppose data sample with two types of events: H 0, H 1 We have found discriminating input variables x 1, x 2, … What decision boundary should we use to select events of type H 1 ? Rectangular cuts? x 2 A linear boundary? H 1 H 0 x 2 H 1 H 0 x 1 A nonlinear one? x 2 H 1 H 0 x 1 How can we decide this in an optimal way ? Let the machine learn it ! CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 17

Multivariate Analysis (MVA) Create test statistics compactifying the input information in a scalar quantity y, with e. g. , y(H 0) 0, y(H 1) 1 G. Cowan, Introduction J. Stelzer, TMVA W. Verkerke, Roo. Fit Large variety of MVA methods, reaching from cuts, over likelihood, to linear and nonlinear discriminants to rule-based approaches like Boosted Decision Trees and Rule. Fit If correlations among the xi are negligible, one can perform maximumlikelihood fit (same principle, see later) CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 18

Example: DØ Single Top Search (I) Electroweak top quark production: s-channel @Tevatron: tb vertex: ≈ 0. 9 pb B. Vachon, Stat. methods for single top search, hep-ex/0612052 t-channel @Tevatron: tqb vertex: ≈ 2 pb Event signature: isolated leptons, 2 -4 jets, 1 b-jet, ET, miss Dominant background: W + jets, multi-jets, tt-bar Use 3 MV discrimination methods: Boosted Decision Trees: 36 signal classes (s/t, e/ , #jets, #b-tags), 49 input variables Bayesian (~ average of many) neural network: 24 input variables, 40 hidden nodes Matrix element: ratio of signal and background PDFs from approx. matrix element of event CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 19

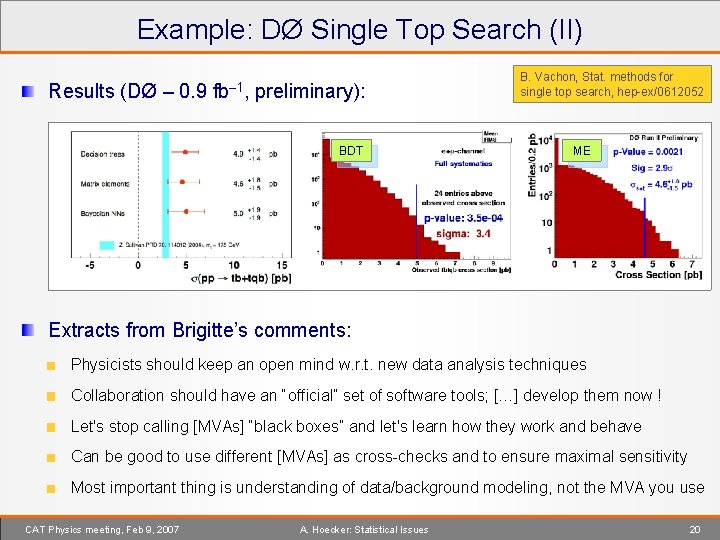
Example: DØ Single Top Search (II) Results (DØ – 0. 9 fb– 1, preliminary): BDT B. Vachon, Stat. methods for single top search, hep-ex/0612052 ME Extracts from Brigitte’s comments: Physicists should keep an open mind w. r. t. new data analysis techniques Collaboration should have an “official” set of software tools; […] develop them now ! Let's stop calling [MVAs] “black boxes” and let's learn how they work and behave Can be good to use different [MVAs] as cross-checks and to ensure maximal sensitivity Most important thing is understanding of data/background modeling, not the MVA you use CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 20

Optimised Analysis Strategy – BABAR Example Kinematic variables Maximum Likelihood Fit Comprise measurement, validation and evaluation of systematics in single analysis step the ML fit A. Farbin, Practical experience from BABAR (figure modified) Also see: ML fits by Bphys group (E. Kneringer) Signal CP Parameters (blind) MVA It would be naïve to believe that all analyses at the LHC Signal/Background Yields could be done that. PIDway, but we should keep in mind B h h’ signal variables candidates Amir’s main message: draw as much information on the Background PDF parameters Flavour nuisance parameters from the data as possible, and do Tagging this simultaneously. Same with the fit of the signal component Signal PDF parameters 0 + - Control sample variables for control sample 119 free parameters in fit; weak (but not negligible) correlations External input: PDF parameters from MC or other control samples not in fit CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 21

Comment on Goodness-Of-Fit Validation It is often said that the unbinned ML fits cannot easily be validated However, there exists a straightforward manner to visualize exactly what the fit does, and to quantitatively determine its goodness AH & Remark by G. Cowan Form the likelihood ratio after fit: Tuple with fit results Compute R(x) for all events entering the ML fit and plot them Produce high-statistics toy MC for all fit components using the likelihood model Plot the events normalised to their relative abundances used/found in fit compare ! CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues Example from BABAR B analysis AH, 2003 22

Statistics Toolkits CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 23

Tools – Summary from the Workshop ROOT (http: //root. cern. ch/) Large number of utilities needed for statistical analysis, including: minimisation, random generation, statistical tests, also TRolke, TLimit… (and a poor man’s TFeldman. Cousins) Roo. Fit (http: //roofit. sf. net/) W. Verkerke ROOT data modelling toolkit for unbinned maximum-likelihood fits and toy MC analysis TMVA (http: //tmva. sf. net/) J. Stelzer ROOT multivariate analysis toolkit for parallel discrimination analysis and data mining s. Plots (ROOT: : TSPlots, physics/0402083) T. Petersen Optimised visualization of maximum-likelihood fit results (not (yet) Roo. Fit based ) Roo. Stats (under development, prototype for Phy. Stat’ 07) K. Cranmer ROOT & Roo. Fit based statistical interpretation with horizontal comparison of methods If you can’t wait, and need p-value for count analysis taking into account background systematics you may checkout catsusy/Stat. Tools CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 24

Blind Analysis CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 25

Blind Analysis (I) Most modern HEP experiments apply blind techniques AH, Blind Analysis Hidden signal box Yield measurements: rare decays, new physics searches, … Hidden answer method Parameter measurements: masses, asymmetries, … Adding or removing unknown number of events Branching fraction, rate measurements Prescaling events (known factor) All types of measurements, notably searches (early discovery) CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 26

Blind Analysis (II) Hiding the result formalises our way to do data analysis AH, Blind Analysis Besides the obvious advantages, blind analysis canalises competition and improves internal review. It strengthens the role of the physics groups Cannot determine general blinding rule, but can suggest to consider and discuss blinding and the technique to use for each analysis individually Most serious objection: could miss/delay obvious new physics signal Could be dealt with by weakening the validation requirements for search analyses… … once ok: unblind the data – and if no clear-cut signal, re-hide signal box and finalise My impression from discussions after the talk: ATLAS is not yet mature for the adventure of blind analysis … ; -) CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues 27

Conclusions D. Froidevaux’s “Motherhood statements” Daniel doesn’t adhere to frequentist vs. Bayesian discussions, and he doesn’t seem to like nuisance parameters either ; -) “Today we have acquired far more sophisticated tools than twenty years ago, but we do not write them always ourselves, which often entails the risk that we do not test them adequately” MC generators, analysis tools ! Need to detain our statistics enthusiasm and first understand: …the detector response …the basic QCD processes and other backgrounds …and validate the MC simulation Fortunately: optimised analysis also helps to reduce background systematics ! (AH) Statistics working group contacts with CMS being prepared (by whom? ) Inter-experiment combination should not wait years to be started CAT Physics meeting, Feb 9, 2007 A. Hoecker: Statistical Issues A. Read 28