Taking Measurements AccuracyPrecision Significant Figures Scientific Notation Accuracy

Taking Measurements Accuracy/Precision Significant Figures Scientific Notation

Accuracy • . Accuracy – Compares a measurement to the true value

Example: Accuracy Who is more accurate when measuring a book that has a true length of 17. 0 cm? Susan: 17. 0 cm, 16. 0 cm, 18. 0 cm, 15. 0 cm • Amy: 15. 5 cm, 15. 0 cm, 15. 2 cm, 15. 3 cm

Precision • • Precision = describes how closely measurements are to each other and how carefully measurements were made Which set is more precise? 18. 2 , 18. 4 , 18. 35 17. 9 , 18. 3 , 18. 85 16. 8 , 17. 2 , 19. 44

Example: Precision Who is more precise when measuring the same 17. 0 cm book? Susan: 17. 0 cm, 16. 0 cm, 18. 0 cm, 15. 0 cm Amy: 15. 5 cm, 15. 0 cm, 15. 2 cm, 15. 3 cm

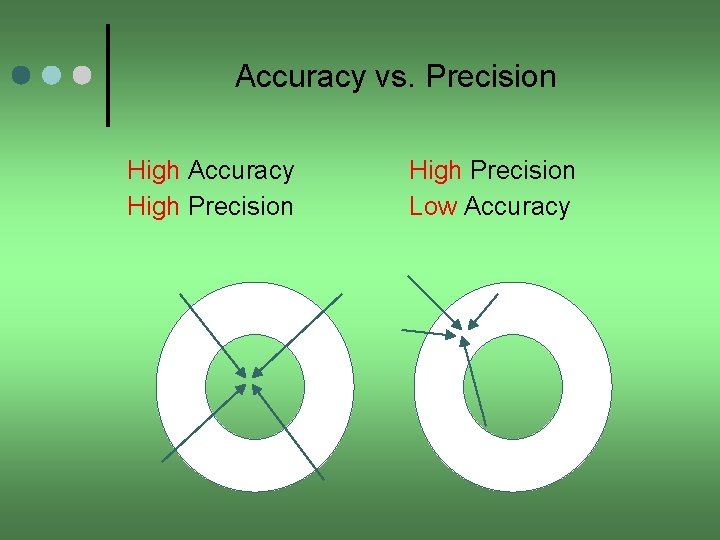
Accuracy vs. Precision High Accuracy High Precision Low Accuracy

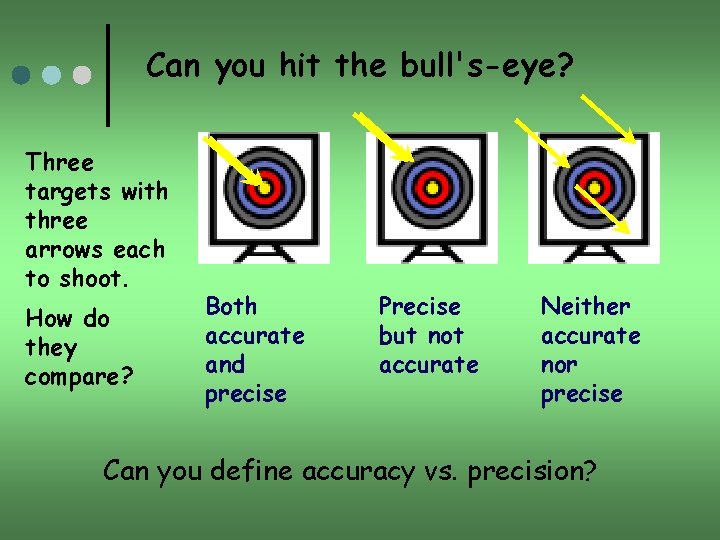
Can you hit the bull's-eye? Three targets with three arrows each to shoot. How do they compare? Both accurate and precise Precise but not accurate Neither accurate nor precise Can you define accuracy vs. precision?

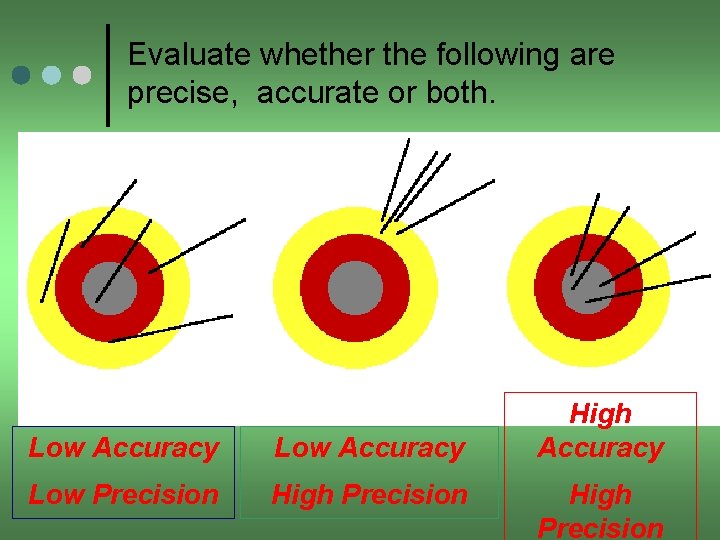
Evaluate whether the following are precise, accurate or both. Low Accuracy Low Precision High Accuracy High Precision

Significant Figures • Scientist use significant figures to determine how precise a measurement is • Significant digits in a measurement include all of the known digits plus one estimated digit

For example… • Look at the ruler below • Each line is 0. 1 cm or 1 mm • You can read that the arrow is on 13. 3 cm • However, using significant figures, you must estimate the next digit • That would give you 13. 30 cm

Let’s try this one • Look at the ruler below • What can you read before you estimate? • 12. 8 cm • Now estimate the next digit… • 12. 85 cm

The same rules apply with all instruments • The same rules apply • Read to the last digit that you know • Estimate the final digit

Let’s try graduated cylinders • Look at the graduated cylinder below • • What can you read with confidence? 56 ml Now estimate the last digit 56. 0 ml

One more graduated cylinder • Look at the cylinder below… • What is the measurement? • 53. 5 ml

So how do we know when a number can be considered significant? There are rules we need to follow!

Rules for Significant figures Rule #1 • All non zero digits are ALWAYS significant • How many significant digits are in the following numbers? • 274 • 3 Significant Figures • 25. 632 • 5 Significant Digits • 8. 987 • 4 Significant Figures

Rule #2 • All zeros between significant digits are ALWAYS significant • How many significant digits are in the following numbers? 504 3 Significant Figures 60002 5 Significant Digits 9. 077 4 Significant Figures

Rule #3 • All FINAL zeros to the right of the decimal ARE significant • Because of this, zeros between a non-zero digit and the final zero ARE significant • How many significant digits are in the following numbers? 32. 0 3 Significant Figures 19. 000 5 Significant Digits 105. 0020 7 Significant Figures

Rule #4 • All zeros that act as place holders are NOT significant • Another way to say this is: zeros are only significant if they are between significant digits OR are the very final thing at the end of a decimal

For example How many significant digits are in the following numbers? 0. 0002 6. 02 x 1023 100. 000 150000 800 1 Significant Digit 3 Significant Digits 6 Significant Digits 2 Significant Digits 1 Significant Digit

Rule #5 • All counting numbers and constants have an infinite number of significant digits • For example: 1 hour = 60 minutes 12 inches = 1 foot 24 hours = 1 day

How many significant digits are in the following numbers? 0. 0073 100. 020 2500 7. 90 x 10 -3 670. 00001 18. 84 2 Significant Digits 6 Significant Digits 2 Significant Digits 3 Significant Digits 4 Significant Digits 1 Significant Digit 4 Significant Digits

Rules Rounding Significant Digits Rule #1 • If the digit to the immediate right of the last significant digit is less that 5, do not round up the last significant digit. • For example, let’s say you have the number 43. 82 and you want 3 significant digits • The last number that you want is the 8 – 43. 82 • The number to the right of the 8 is a 2 • Therefore, you would not round up & the number would be 43. 8

Rounding Rule #2 • If the digit to the immediate right of the last significant digit is greater that a 5, you round up the last significant figure • Let’s say you have the number 234. 87 and you want 4 significant digits • 234. 87 – The last number you want is the 8 and the number to the right is a 7 • Therefore, you would round up & get 234. 9

Rounding Rule #3 • If the number to the immediate right of the last significant is a 5, and that 5 is followed by a non zero digit, round up • 78. 657 (you want 3 significant digits) • The number you want is the 6 • The 6 is followed by a 5 and the 5 is followed by a non zero number • Therefore, you round up • 78. 7

Let’s try these examples… 200. 99 (want 3 SF) 201 18. 22 (want 2 SF) 18 135. 50 (want 3 SF) 135 0. 00299 (want 1 SF) 0. 003 98. 59 (want 2 SF) 99

Sig Figs Example #1 How many significant figures are in the following number: 0. 0032 a. 1 b. 3 c. 2 d. 4

Sig Figs Example #1 How many significant figures are in the following number: 0. 0032 a. 1 b. 3 c. 2 d. 4

Sig Figs Example #2 Which of the following has 4 significant figures? a. 0. 00302 b. 4. 40 x 10 -4 c. 34, 001 d. 3, 401

Sig Figs Example #2 Which of the following has 4 significant figures? a. 0. 00302 b. 4. 40 x 10 -4 c. 34, 001 d. 3, 401

Adding/Subtracting Sig Figs • Use only the # of sig figs as the last place value of the least precise measurement Example: 142 - 14. 56 = 127. 44 142 is the least precise so the answer is 127.

Add/Subtract Example Add the following numbers with your answer having the correct amount of significant figures. 127. 54 + 233 + 134. 555

Add/Subtract Example Add the following numbers with your answer having the correct amount of significant figures. 127. 54 + 233 + 134. 555 = 495. 095 The answer is 495

Multiplying/Dividing Sig Figs • Use the same amount of sig figs as the number with the least amount of significant figures Example: 118. 88 x 525 = 62, 412 The correct answer is 62, 400 (3 sig figs)

Mult/Divide Example Divide the following numbers with your answer having the correct number of significant figures. 170, 666 4, 208 =

Mult/Divide Example Divide the following numbers with your answer having the correct number of significant figures. 170, 666 4, 208 = 40. 5575095 The correct answer is 40. 56 (4 sig figs)

Be the Teacher! Left Side of the Room: • Become experts on adding/subtracting with sig figs • Chat with others in your group • Create examples/explanations Right Side of the Room: • Become experts on multiplying/dividing with sig figs • Chat with others in your group • Create examples/explanations

Be the Teacher Then, choose a partner from the other side of the room and…. Teach them

Scientific Notation • Scientific notation is used to express very large or very small numbers • I consists of a number between 1 & 10 followed by x 10 to an exponent • The exponent can be determined by the number of decimal places you have to move to get only 1 number in front of the decimal

Large Numbers • If the number you start with is greater than 1, the exponent will be positive • Write the number 39923 in scientific notation • First move the decimal until 1 number is in front –> 3. 9923 • Now add x 10 –> 3. 9923 x 10 • Now count the number of decimal places that you moved (4) • Since the number you started with was greater than 1, the exponent will be positive • 3. 9923 x 10 4

Small Numbers • If the number you start with is less than 1, the exponent will be negative • Write the number 0. 0052 in scientific notation • First move the decimal until 1 number is in front – 5. 2 • Now at x 10 – 5. 2 x 10 • Now count the number of decimal places that you moved (3) • Since the number you started with was less than 1, the exponent will be negative • 5. 2 x 10 -3

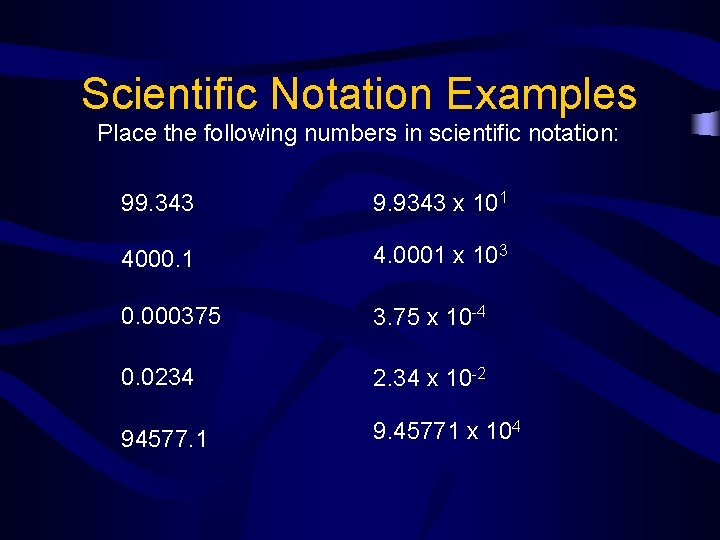
Scientific Notation Examples Place the following numbers in scientific notation: 99. 343 9. 9343 x 101 4000. 1 4. 0001 x 103 0. 000375 3. 75 x 10 -4 0. 0234 2. 34 x 10 -2 94577. 1 9. 45771 x 104

Going from Scientific Notation to Ordinary Notation • You start with the number and move the decimal the same number of spaces as the exponent. • If the exponent is positive, the number will be greater than 1 • If the exponent is negative, the number will be less than 1

Going to Ordinary Notation Examples Place the following numbers in ordinary notation: 3 x 106 6. 26 x 109 5 x 10 -4 8. 45 x 10 -7 2. 25 x 103 3000000 6260000000 0. 0005 0. 000000845 2250