Tablouri unidimensionale vectori Introducere Definiie Declararea tabloului Iniializarea

Tablouri unidimensionale (vectori) • Introducere • Definiție • Declararea tabloului • Inițializarea tabloului • Accesul la elemente • Operații posibile Prof. Informatica: Bokor Cristina Liceul Tehnologic “Dumitru Dumitrescu” Buftea

Tablouri unidimensionale Numărul de variabile ce pot fi declarate și utilizate într-o aplicație Necesitate este limitat. Există aplicații care necesită memorarea și prelucrarea unor serii de sute și mii de valori. Accesarea unui număr mare de variabile este anevoios și generator de erori. Pentru a rezolva această problemă au fost create structuri de date (colecții de date) specializate ce ocupă spații de memorie învecinate și în care aranjarea lor este interdependentă. Exemple ! Memorarea și prelucrarea mediilor de absolvire pentru totalitatea elevilor unui liceu Memorarea și identificarea numerelor de înmatriculare ale autovehiculelor dintr-un județ Evidența biletelor eliberate (vândute) către clienți cu ocazia unui spectacol de anvergură (de exemplul pe un stadion)

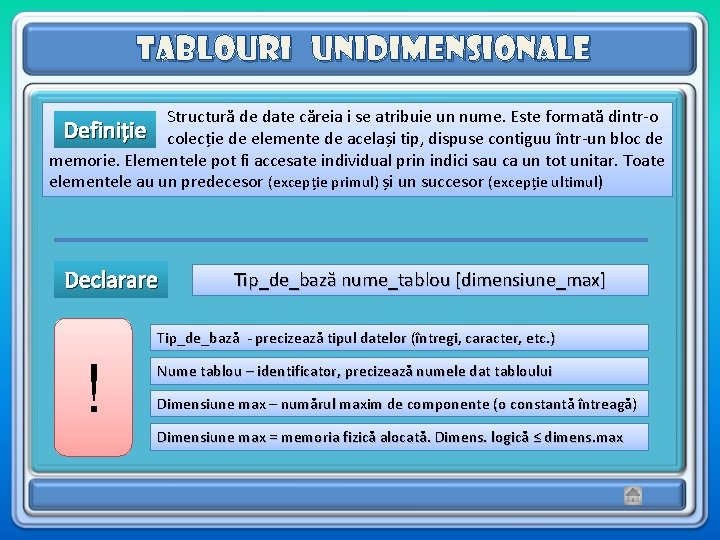
Tablouri unidimensionale Structură de date căreia i se atribuie un nume. Este formată dintr-o Definiție colecție de elemente de același tip, dispuse contiguu într-un bloc de memorie. Elementele pot fi accesate individual prin indici sau ca un tot unitar. Toate elementele au un predecesor (excepție primul) și un succesor (excepție ultimul) Declarare Tip_de_bază nume_tablou [dimensiune_max] Tip_de_bază - precizează tipul datelor (întregi, caracter, etc. ) ! Nume tablou – identificator, precizează numele dat tabloului Dimensiune max – numărul maxim de componente (o constantă întreagă) Dimensiune max = memoria fizică alocată. Dimens. logică ≤ dimens. max

Tablouri unidimensionale Declararea tablourilor int vec [3]; vectorul (poate) conține 3 elemente de tip int const int max=99; int vec[max]; vectorul (poate) conține 99 elem. float vec [99] ; vectorul (poate) conține 99 elem de tip float char vec [3] ; vectorul (poate) conține 3 elemente de tip char int sir[3*3+2] ; vectorul “sir”(poate) conține 11 elemente de tip char int a[99], b[99] ; au fost declarați doi vectori a, b

Tablouri unidimensionale Exemple incorecte de declarare pentru că : integer vec [99] ; tipul integer nu e definit in C++ float vec [max] ; “max” este declarat ca variabilă char vec 1 [3*9] ; în nume există caracterul “spațiu” int char[99] ; s-a folosit ca nume cuvântul rezervat “char” int char[3] ={“eroare”} ; lungimea declarata este mai mare ca max[3]

Tablouri unidimensionale Inițializarea tablourilor int vec [3]; vectorul (poate) conține 3 elemente de tip int vec [3] = {5, 6, 7}; vectorul conține elementele din acoladă float vec [] = {1. 4, -2, 1. 2 e+2}; char vec [3] = {‘a’, ‘b’, ‘c’}; char sir[]={“vector”} ; conținutul este indicat în acoladă vectorul conține caracterele a, b , c vectorul “sir” conține 6 elemente de tip char sir[3]={char(97), char(98)} ; vectorul conține caracterele a, b

Tablouri unidimensionale Accesul la elementele tabloului : Se folosește numele tabloului urmat de indicele (numărul de ordine) elementului referit, înscris între paranteze pătrate. Ex. nume[indice] int vec [4] = {12, 23, 34, 45}; 12 23 34 45 Referirea la elemente V[0] V[1] V[2] V[3] Primul element din vector are numărul de ordine (indicele) zero ! Astfel, elementul cu număr de ordine 0 din vector este 12, elementul al 2 -lea este 23 și elementul 45 este al 4 -lea element din vector (are indicele 3).

Tablouri unidimensionale Operații posibile Inițializarea (generarea) tabloului unidimensional Mememorarea și afișarea elementelor unui tablou Parcurgerea și căutarea elementelor memorate în tablou Prelucrarea elementelor tabloului (sume, medii , căutări, maxime, verificări) Ștergerea sau adaugarea unui element din tablou Sortarea elementelor unui tablou Interclasarea (concatenarea) a doi vectori sortați anterior

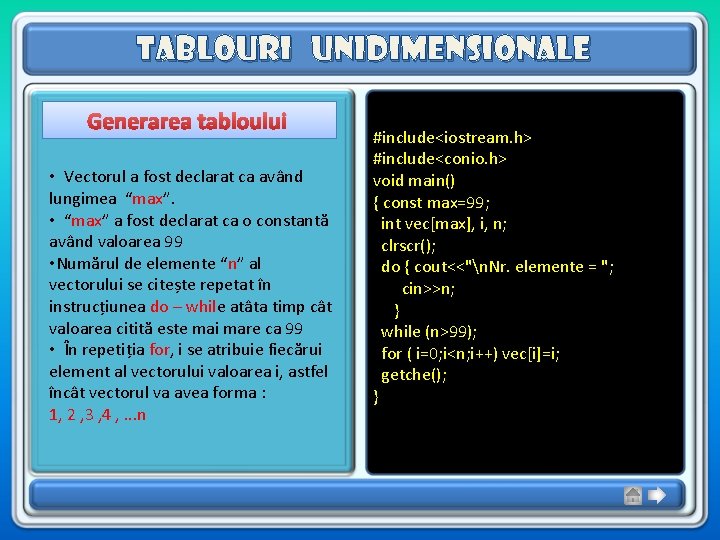
Tablouri unidimensionale Generarea tabloului • Vectorul a fost declarat ca având lungimea “max”. • “max” a fost declarat ca o constantă având valoarea 99 • Numărul de elemente “n” al vectorului se citește repetat în instrucțiunea do – while atâta timp cât valoarea citită este mai mare ca 99 • În repetiția for, i se atribuie fiecărui element al vectorului valoarea i, astfel încât vectorul va avea forma : 1, 2 , 3 , 4 , . . . n #include<iostream. h> #include<conio. h> void main() { const max=99; int vec[max], i, n; clrscr(); do { cout<<"n. Nr. elemente = "; cin>>n; } while (n>99); for ( i=0; i<n; i++) vec[i]=i; getche(); }

Tablouri unidimensionale Crearea și afisarea tabloului • Numărul “n” de elemente al vectorului se citește de la tastatură în mod repetat atâta timp cât numărul citit este mai mare ca 99 • În repetiția for, se citește de la tastatură valoarea fiecărui element al vectorului (citirea se face simultan cu memorarea în vector) • Afișarea se face în interiorul structurii repetitive “for”, între elementele vectorului fiind un spațiu liber (cout<<vec[i]<<" “; ) #include<iostream. h> #include<conio. h> void main() { int vec[999], i, n; clrscr(); do { cout<<"n. Nr. elemente = "; cin>>n; } while (n>99); for ( i=0; i<n; i++) { cout<<"n. Elementul = "; cin>>vec[i]; } cout<<"n. Vectorul este : "; for (i=0; i<n; i++) cout<<vec[i]<<" "; getche(); }

Tablouri unidimensionale Căutarea unui element • Numărul “n” de elemente al vectorului se citește de la tastatură • În repetiția for, se citește de la tastatură valoarea fiecărui element al vectorului (citirea se face simultan cu memorarea în vector) • Pentru căutarea elementului “k” se parcurge vectorul și fiecare element al său se compară dacă este egal cu “k”. • Dacă se găsește o egalitate, variabila “este” se modifică din 0 în 1 și variabila “poz” memorează valoarea lui “i” (unde a fost găsit elementul). • Afișarea se face funcție de “este”. #include<iostream. h> #include<conio. h> void main() { int vec[999], i, n, este=0, k, poz; cout<<"n. Nr. elemente = "; cin>>n; for ( i=0; i<n; i++) { cout<<"n. Elementul = "; cin>>vec[i]; } cout<<"Cautam elementul : "; cin>>k; for (i=0; i<n; i++) if (vec[i]==k) { poz=i; este=1; } if (este == 1) cout<<“Gasit pe pozitia "<<poz; else cout<<k<<“ nu e in vector"; getche(); }

Tablouri unidimensionale Căutarea binară în vector • Algoritmul presupune că vectorul este sortat anterior • Căutarea se execută prin înjumătățiri repetate a intervalului de căutare rezultând doi subvectori x[st]…x[mij-1] și x[mij+1]…x[dr] (st = indicele primului element din stânga, dr = indice din dreapta, mij = indice element central) • Algoritmul identifică subvectorul în care poate fi elementul căutat divizându-l succesiv dacă este cazul, până la găsirea elementului căutat sau până când subvectorul nu mai poate fi divizat (elementul nu a fost găsit) #include<iostream. h> #include<conio. h> void main() { int a[9]={3, 5, 6, 7, 8, 9, 19, 99, 101}, n=0, x, este=0, st=0, dr, mi; while (a[n+1]!=NULL) { cout<<a[n]<<" "; n++; } dr=n-1; cout<<"n. Elementul cautat = "; cin>>x; while (st<=dr && !este) { mi=(st+dr)/2; if(a[mi]==x) este=1; else if (x<a[mi]) dr=mi-1; else st=mi+1; } if (st>dr) cout<<"Element negasit !"; else cout<<“Gasit pe pozitia "<<mi+1; getch(); }

Tablouri unidimensionale Sume în tablou • Variabila “sum” este inițializată cu 0 • În repetiția do-while, se citește numărul de elemente “n” până când acesea este mai mic ca 99 • Simultan cu citirea elementelor vectorului (în repetiția “for”) suma se incrementează cu valoarea elementului de vector citit adică altfel scris : suma = suma + vec[i] • La terminarea repetiției, suma elementelor citite este afișată #include<iostream. h> #include<conio. h> void main() { int vec[999], i, n, sum=0; clrscr(); do { cout<<"n. Nr. elemente = "; cin>>n; } while (n>99); for ( i=0; i<n; i++) { cout<<"n. Elementul = "; cin>>vec[i]; sum+=vec[i]; } cout<<"n. Suma elementelor = " <<sum; getche(); }

Tablouri unidimensionale Numărarea unor elemente • Variabila “par” este inițializată cu 0. Ea va număra câte elemente sunt pare • În repetiția do-while, se citește numărul de elemente “n” până când acesta este mai mic ca 99 • După memorarea elementelor, parcurgem vectorul (cu repetiția“for”) și comparăm pentru fiecare element dacă restul împărțirii lui la 2 este 0. (vec[i] % 2 == 0). • Dacă da, (restul = 0) atunci înseamnă că elementul este par și contorul “par” crește cu o unitate. • Număr impare = total – par #include<iostream. h> #include<conio. h> void main() { int vec[999], i, n, par=0; clrscr(); do { cout<<"n. Nr. elemente = "; cin>>n; } while (n>99); for ( i=0; i<n; i++) { cout<<"n. Elementul = "; cin>>vec[i]; } for (i=0; i<n; i++) if (vec[i]%2 == 0) par++; cout<<"n. Elem. pare = "<<par; cout<<"Elem. impare = "<<n-par; getche(); }

Tablouri unidimensionale Determinare min, max • Variabilele “min” și “max” sunt inițializate cu valoarea primului element de vector “vec[0]”. • După memorarea elementelor, parcurgem vectorul (cu repetiția“for”) • Comparăm pentru fiecare element dacă este mai mic ca “min”. Dacă da, atunci acesta devine “min” min=vec[i]) • Comparăm și dacă este mai mare ca “max”. Dacă da, acestuia i se atribuie valoarea lui “max” (max=vec[i]). • La terminarea parcurgerii, valorile “min” și “max” sunt afișate #include<iostream. h> #include<conio. h> void main() { int vec[999], i, n, max, min; cout<<"n. Nr. elemente = "; cin>>n; } for ( i=0; i<n; i++) { cout<<"n. Elementul = " cin>>vec[i]; } max = min = vec[0]; for (i=0; i<n; i++) { if (vec[i]>max) max = vec[i]; if (vec[i]<min) min = vec[i]; } cout<<"n. Element max = "<<max; cout<<"n. Element min = "<<min; getche(); }

Tablouri unidimensionale Adaugare element la capăt • Vectorul este afișat folosind instrucțiunea “while” în mod repetat, atâta timp cât elementul de afișat este diferit de NULL • Variabila “i” reține lungimea vectorului, crescând cu o unitate după fiecare afișare (“i++”) • După ultima afișare, lungimea vectorului crește cu o unitate, astfel se crează o locație suplimentară pentru adăugarea unui element nou. • Elementul ce se adaugă la capăt se introduce așadar pe poziția “i” (pe ultima poziție) #include<iostream. h> #include<conio. h> void main() { int vec[]={1, 2, 3, 4, 5, 6, 7, 8, 9}, i=0; clrscr(); while (vec[i]!=NULL) { cout<<vec[i]<<" "; i++; } cout<<"Element = "; cin>>vec[i]; i=1; do { cout<<vec[i-1]<<" "; i++; } while (vec[i] != NULL); getche(); }

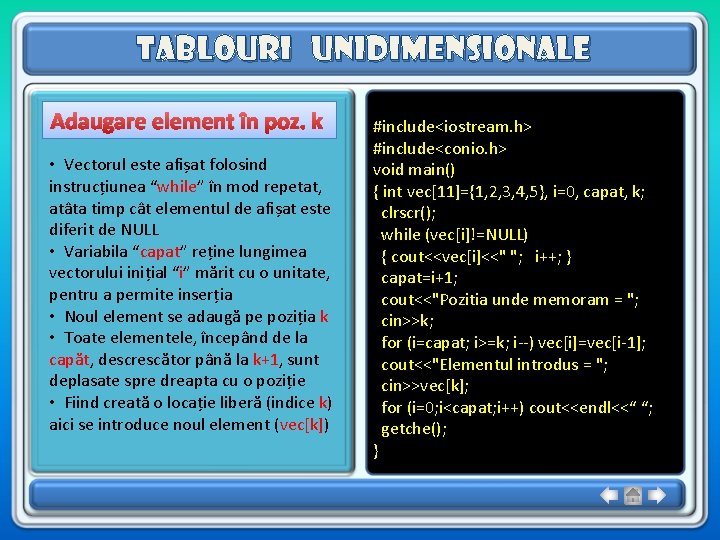
Tablouri unidimensionale Adaugare element în poz. k • Vectorul este afișat folosind instrucțiunea “while” în mod repetat, atâta timp cât elementul de afișat este diferit de NULL • Variabila “capat” reține lungimea vectorului inițial “i” mărit cu o unitate, pentru a permite inserția • Noul element se adaugă pe poziția k • Toate elementele, începând de la capăt, descrescător până la k+1, sunt deplasate spre dreapta cu o poziție • Fiind creată o locație liberă (indice k) aici se introduce noul element (vec[k]) #include<iostream. h> #include<conio. h> void main() { int vec[11]={1, 2, 3, 4, 5}, i=0, capat, k; clrscr(); while (vec[i]!=NULL) { cout<<vec[i]<<" "; i++; } capat=i+1; cout<<"Pozitia unde memoram = "; cin>>k; for (i=capat; i>=k; i--) vec[i]=vec[i-1]; cout<<"Elementul introdus = "; cin>>vec[k]; for (i=0; i<capat; i++) cout<<endl<<“ “; getche(); }

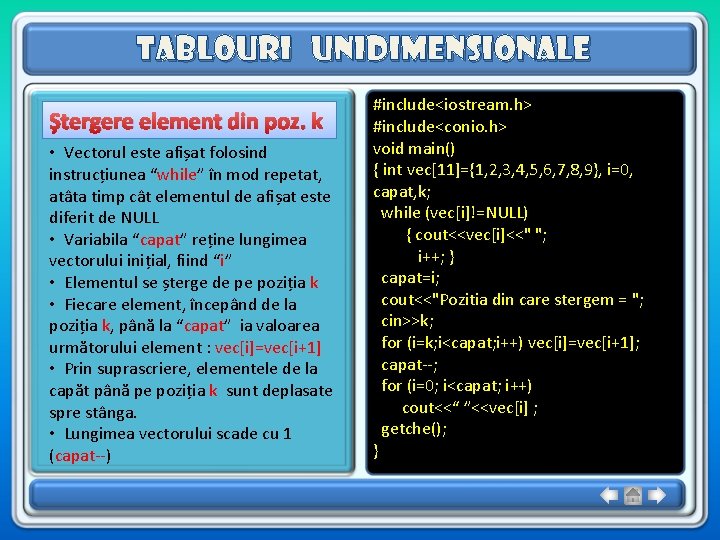
Tablouri unidimensionale Ștergere element din poz. k • Vectorul este afișat folosind instrucțiunea “while” în mod repetat, atâta timp cât elementul de afișat este diferit de NULL • Variabila “capat” reține lungimea vectorului inițial, fiind “i” • Elementul se șterge de pe poziția k • Fiecare element, începând de la poziția k, până la “capat” ia valoarea următorului element : vec[i]=vec[i+1] • Prin suprascriere, elementele de la capăt până pe poziția k sunt deplasate spre stânga. • Lungimea vectorului scade cu 1 (capat--) #include<iostream. h> #include<conio. h> void main() { int vec[11]={1, 2, 3, 4, 5, 6, 7, 8, 9}, i=0, capat, k; while (vec[i]!=NULL) { cout<<vec[i]<<" "; i++; } capat=i; cout<<"Pozitia din care stergem = "; cin>>k; for (i=k; i<capat; i++) vec[i]=vec[i+1]; capat--; for (i=0; i<capat; i++) cout<<“ ”<<vec[i] ; getche(); }

Tablouri unidimensionale Sortări A sorta un vector înseamnă a-l reordona după anumite criterii. • Sortare prin metoda bulelor Criterii uzuale folosite în sortare : o numeric crescător o numeric descrescător o alfabetic crescător (A. . . Z) o alfabetic descrescător (Z. . . A) Exemplu tablou nesortat = {2, 7, 9, 1, 0, 5, 4} tablou sortat = {0, 1, 2, 4, 5, 7, 9} • Sortare prin inserție Există mai multe metode de sortare bazate pe algoritmi diferiți. În continuare sunt prezentate câteva metode utilizate în acest scop. • Sortare prin inserție directă • Sortare prin numărare • Sortare prin inserție rapidă • Sortare prin selecție directă

Tablouri unidimensionale Sortare - metoda bulelor • Elementele de vector se afișază până când elementul de afișat este NULL • Variabilele: “n”= lungimea vectorului “inv”= variabilă pentru inversarea elementelor, “ok”=comutator (inițial 1) • Se parcurge vectorul și se compară elementele învecinate. Dacă elementul din stânga e mai mic decât vecinul din dreapta (vec[i]>vec[i+1]), ele se interschimbă și comutatorul “ok” devine 0. • Interschimbarea (a două câte două elemente) continuă atâta timp cât comutatorul “ok” este egal cu 0 #include<iostream. h> #include<conio. h> void main() { int vec[99]={7, 5, 29, 9}, i=0, n, ok, inv; while (vec[i] != NULL) { cout<<vec[i]<<" "; i++; } n = i; do { ok=1; for (i=0; i<n-1; i++) if (vec[i]>vec[i+1]) { inv=vec[i]; vec[i]=vec[i+1]; vec[i+1]=inv; ok=0; } } while (ok==0); cout<<endl<<“Vectorul sortat = “; for (i=0; i<n; i++) cout<<" "<<vec[i]; }

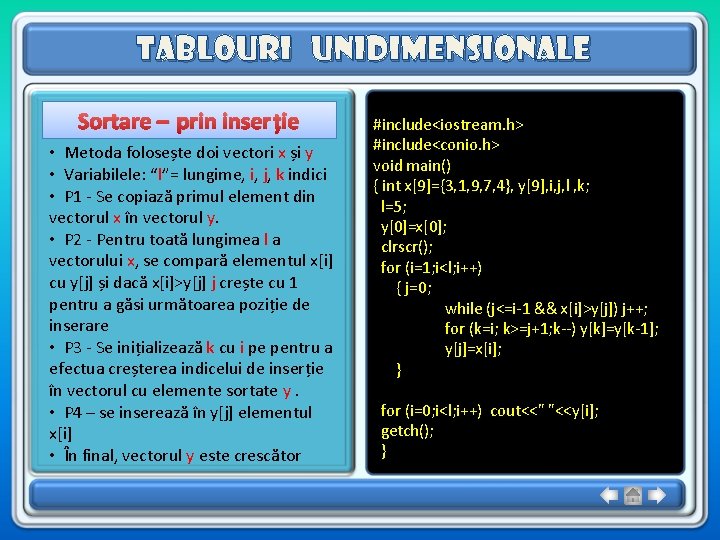
Tablouri unidimensionale Sortare – prin inserție • Metoda folosește doi vectori x și y • Variabilele: “l”= lungime, i, j, k indici • P 1 - Se copiază primul element din vectorul x în vectorul y. • P 2 - Pentru toată lungimea l a vectorului x, se compară elementul x[i] cu y[j] și dacă x[i]>y[j] j crește cu 1 pentru a găsi următoarea poziție de inserare • P 3 - Se inițializează k cu i pe pentru a efectua creșterea indicelui de inserție în vectorul cu elemente sortate y. • P 4 – se inserează în y[j] elementul x[i] • În final, vectorul y este crescător #include<iostream. h> #include<conio. h> void main() { int x[9]={3, 1, 9, 7, 4}, y[9], i, j, l , k; l=5; y[0]=x[0]; clrscr(); for (i=1; i<l; i++) { j=0; while (j<=i-1 && x[i]>y[j]) j++; for (k=i; k>=j+1; k--) y[k]=y[k-1]; y[j]=x[i]; } for (i=0; i<l; i++) cout<<" "<<y[i]; getch(); }

Tablouri unidimensionale Sortare prin inserție directă • Metoda împarte vectorul în doi subvectori : sursă x[i]…x[l-1] și destinație x[0]…x[i-1] • Variabila inv memorează elementul x[i] pe timpul deplasării spre dreapta în interiorul vectorului destinație • Variabila i împarte vectorul în subvectori și la fiecare împărțire crește cu 1 până când are valoarea n-1 (subvectorul sursă nu mai conține elemente) • Variabila j se inițializează cu indicele ultimului element din subvectorul destinație #include<iostream. h> #include<conio. h> void main() { int x[9]={3, 1, 9, 7, 4}, i, j, l , inv; l=5; clrscr(); for (i=1; i<l; i++) { inv=x[i]; j=i-1; while (j>0 && inv<x[j]) { x[j+1]=x[j]; j--; } if (inv>=x[j]) x[j+1]=inv; else {x[1]=x[0]; x[0]=inv; } } for (i=0; i<l; i++) cout<<" "<<x[i]; getch(); }

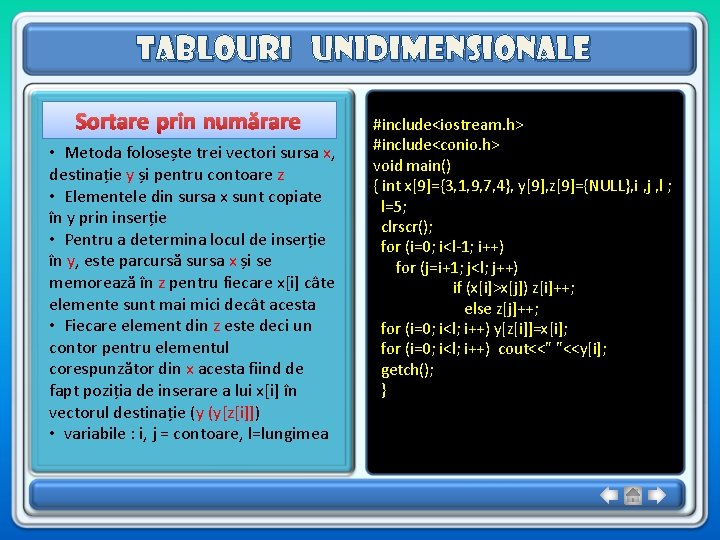
Tablouri unidimensionale Sortare prin numărare • Metoda folosește trei vectori sursa x, destinație y și pentru contoare z • Elementele din sursa x sunt copiate în y prin inserție • Pentru a determina locul de inserție în y, este parcursă sursa x și se memorează în z pentru fiecare x[i] câte elemente sunt mai mici decât acesta • Fiecare element din z este deci un contor pentru elementul corespunzător din x acesta fiind de fapt poziția de inserare a lui x[i] în vectorul destinație (y (y[z[i]]) • variabile : i, j = contoare, l=lungimea #include<iostream. h> #include<conio. h> void main() { int x[9]={3, 1, 9, 7, 4}, y[9], z[9]={NULL}, i , j , l ; l=5; clrscr(); for (i=0; i<l-1; i++) for (j=i+1; j<l; j++) if (x[i]>x[j]) z[i]++; else z[j]++; for (i=0; i<l; i++) y[z[i]]=x[i]; for (i=0; i<l; i++) cout<<" "<<y[i]; getch(); }

Tablouri unidimensionale Sortare prin inserție rapidă • Metoda folosește împărțirea vectorului în doi subvectori sursă și destinație ca la inserția directă • Căutarea poziției unde se inserează elementul x[i] din subvectorul sursă se face prin algoritmul de căutare binară. • Astfel subvectorul destinație se împarte în doi subvectori și se testează relația dintre elementul de mijloc și elementul a[i] • Se stabilește dacă inserția are loc în dreapta sau stânga față de mijloc • Operația de împărțire a subvectorului continuă până se găsește poziția de inserat a lui a[i] #include<iostream. h> #include<conio. h> void main() { int x[9]={3, 1, 9, 7, 4}, i, j, l=5, inv, st, dr, mi; for (i=1; i<l; i++) { inv=x[i]; st=0; dr=i-1; while (st<dr) { mi=(st+dr)/2; if (inv<x[mi]) dr=mi-1; else st=mi+1; } j=i-1; while (j>=st) { x[j+1]=x[j]; j--; } x[st]=inv; } for (i=0; i<l; i++) cout<<" "<<x[i]; getch(); }

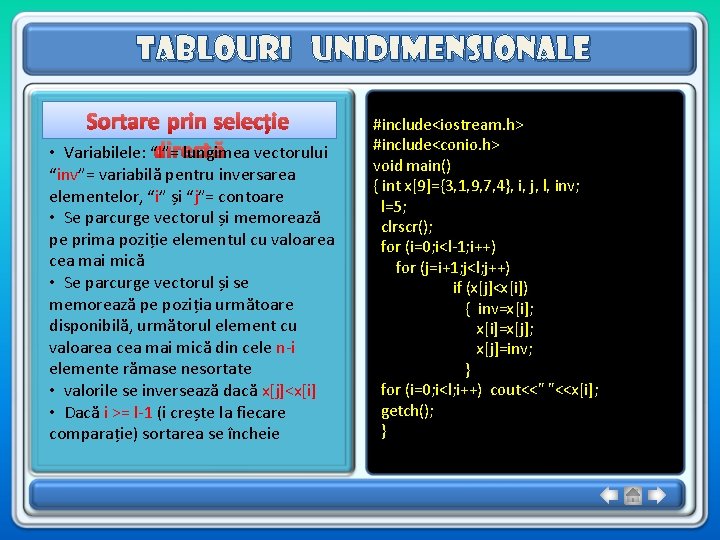
Tablouri unidimensionale Sortare prin selecție directă Variabilele: “l”= lungimea vectorului • “inv”= variabilă pentru inversarea elementelor, “i” și “j”= contoare • Se parcurge vectorul și memorează pe prima poziție elementul cu valoarea cea mai mică • Se parcurge vectorul și se memorează pe poziția următoare disponibilă, următorul element cu valoarea cea mai mică din cele n-i elemente rămase nesortate • valorile se inversează dacă x[j]<x[i] • Dacă i >= l-1 (i crește la fiecare comparație) sortarea se încheie #include<iostream. h> #include<conio. h> void main() { int x[9]={3, 1, 9, 7, 4}, i, j, l, inv; l=5; clrscr(); for (i=0; i<l-1; i++) for (j=i+1; j<l; j++) if (x[j]<x[i]) { inv=x[i]; x[i]=x[j]; x[j]=inv; } for (i=0; i<l; i++) cout<<" "<<x[i]; getch(); }

Tablouri unidimensionale Interclasare vectori (sortați) Intreclasarea presupune reuniunea a • doi vectori care au fost sortați anterior. • Algoritmul parcurge cei doi vectori sursă a și b și compară elementele. • Elementul determinat a avea valoarea cea mai mică din sursă este memorat în vectorul destinație c • Operația de comparare și memorare în destinație continuă până când se ajunge la capătul unuia dintre cele două surse • Elementele rămase în celălalt vector sunt memorate la capătul vectorului destinație c #include<iostream. h> #include<conio. h> void main() { int a[9]={3, 5, 9, 19, 99}, b[9]={1, 7, 33}, c[99], i, j, n=5, m=3, k; i=0; j=0; k=0; while ((i<n) && (j<m)) { if (a[i]<b[j]) { c[k]=a[i]; i++; k++; } else { c[k]=b[j]; j++; k++; } } if (i<n) while (i<n) { c[k]=a[i]; k++; i++; } else while (j<m) { c[k]=b[i]; k++; j++; } for (i=0; i<k; i++) cout<<" "<<c[i]; getch(); }

Unități de conținut Exemple de activități de învățare • elevii, utilizând o aplicație software adecvată indicată de profesor: o platformă online de învățare-evaluare, vor rezolva o serie de probleme şi exerciții specifice temei date, din culegerea online conținută de acea platformă • - elevii vor primi un feedback imediat, vor discuta împreună cu profesorul soluțiile propuse, îşi vor corecta eventualele erori sau iși vor îmbunătății rezolvările

Instrumente TIC propuse -videoproiector - software de mamagement al clasei (Net. Support. School). - Platfome de învățare: AEL, INSAM, . campion http: //www. elearning. ro/cisco -in-educatia-preuniversitara

https: //insam. softwin. ro/insam/my. Test. do

http: //campion. edu. ro/arhiva/index. php? page=problem&action=view&id=569

http: //portal. edu. ro/materiale_ael/index. php? locale=ro_RO. utf-8