Tables Patterns and Graphs LINEAR PATTERNS Linear number

Tables, Patterns and Graphs

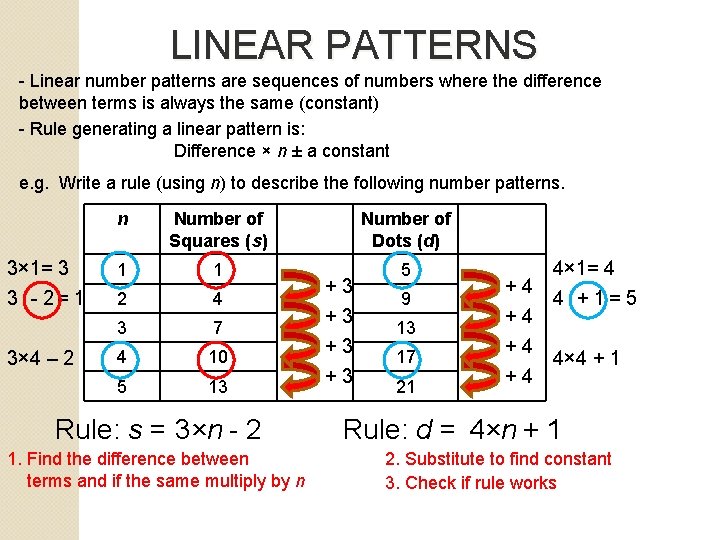
LINEAR PATTERNS - Linear number patterns are sequences of numbers where the difference between terms is always the same (constant) - Rule generating a linear pattern is: Difference × n ± a constant e. g. Write a rule (using n) to describe the following number patterns. 3× 1= 3 3 - 2= 1 3× 4 – 2 n Number of Squares (s) Number of Dots (d) 1 1 5 2 4 3 7 4 10 5 13 Rule: s = 3×n - 2 1. Find the difference between terms and if the same multiply by n +3 +3 9 13 17 21 4× 1= 4 +4 4 + 1= 5 +4 +4 4× 4 + 1 +4 Rule: d = 4×n + 1 2. Substitute to find constant 3. Check if rule works

SIMPLE QUADRATIC PATTERNS - Quadratic number patterns are sequences of numbers where the difference between terms is not the same and the rule contains a squared term - You need to halve the difference of the differences to find the squared term - i. e. If the difference of the differences is a 2, the rule contains 1 n 2 e. g. Write a rule for the following pattern n Term (T) 1 4 2 7 3 12 4 19 5 28 Rule: T = 1 n 2+ 3 +3 +5 +7 +9 +2 +2 +2 1× 12 = 1 1 + 3= 4 42 + 3 = 19 nd 1. Find the difference between terms 3. Halve the 2 difference to find the n 2 rule 2. If difference is not the same, find 4. Substitute to find constant the difference of the differences! 5. Check if rule works

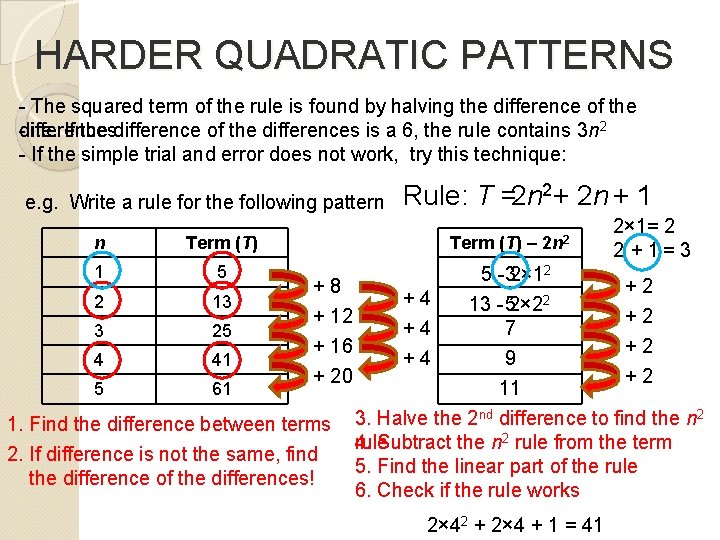
HARDER QUADRATIC PATTERNS - The squared term of the rule is found by halving the difference of the - i. e. If the difference of the differences is a 6, the rule contains 3 n 2 differences - If the simple trial and error does not work, try this technique: e. g. Write a rule for the following pattern n Term (T) 1 5 Rule: T =2 n 2+ 2 n + 1 Term (T) – 2 n 2 2× 1= 2 2 + 1= 3 5 - 32× 12 +8 +2 +4 2 2 13 13 - 52× 2 + 12 +2 + 4 7 3 25 + 16 +2 +4 9 4 41 + 20 +2 11 5 61 nd 2 1. Find the difference between terms 3. Halve the 2 difference to find the n rule 4. Subtract the n 2 rule from the term 2. If difference is not the same, find 5. Find the linear part of the rule the difference of the differences! 6. Check if the rule works 2× 42 + 2× 4 + 1 = 41

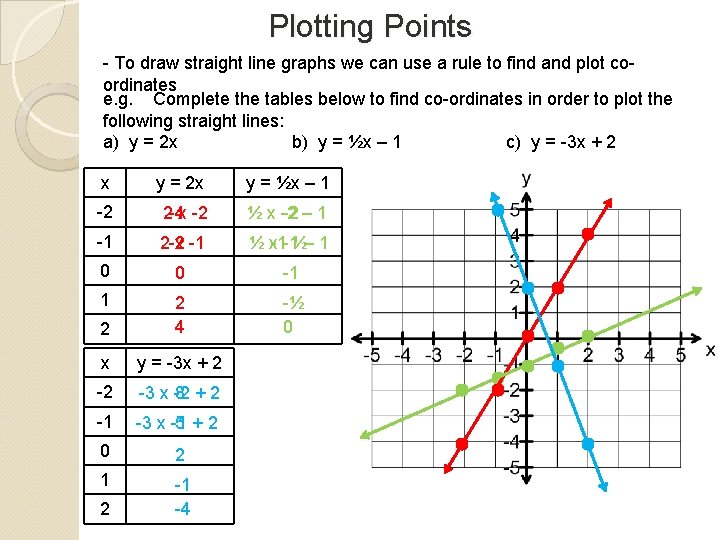
Plotting Points - To draw straight line graphs we can use a rule to find and plot coordinates e. g. Complete the tables below to find co-ordinates in order to plot the following straight lines: a) y = 2 x b) y = ½x – 1 c) y = -3 x + 2 x y = 2 x y = ½x – 1 -2 2 -4 x -2 ½ x -2 – 1 -1 2 -2 x -1 ½ x-1 -1½– 1 0 0 -1 1 2 2 4 -½ 0 x y = -3 x + 2 -2 -3 x -2 8 +2 -1 -3 x -1 5 +2 0 2 1 -1 -4 2

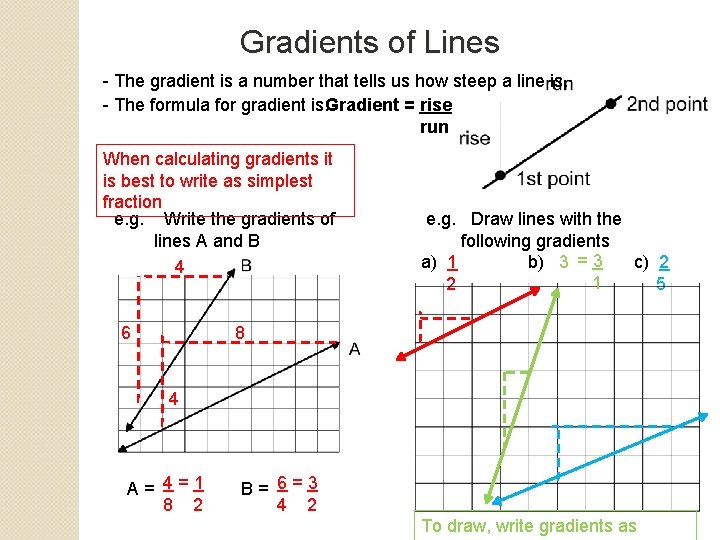
Gradients of Lines - The gradient is a number that tells us how steep a line is. - The formula for gradient is: Gradient = rise run When calculating gradients it is best to write as simplest fraction e. g. Write the gradients of lines A and B 4 6 e. g. Draw lines with the following gradients a) 1 b) 3 = 3 c) 2 1 2 5 8 4 A= 4=1 8 2 B= 6=3 4 2 To draw, write gradients as

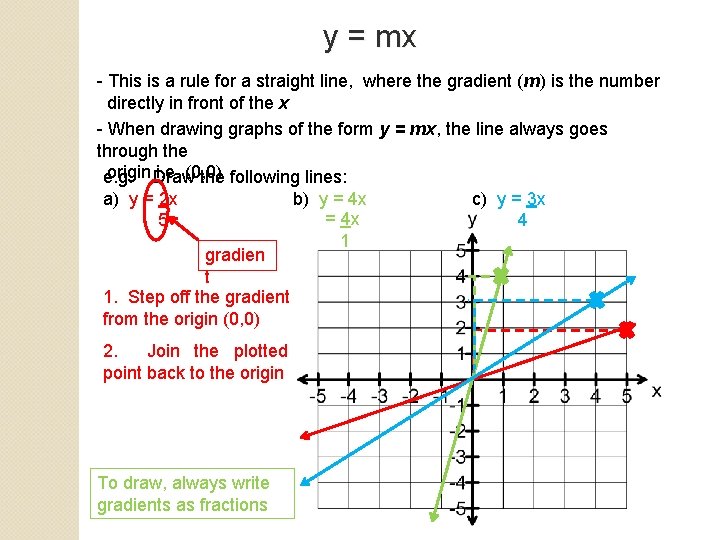
y = mx - This is a rule for a straight line, where the gradient (m) is the number directly in front of the x - When drawing graphs of the form y = mx, the line always goes through the origin Draw i. e. (0, 0) e. g. the following lines: a) y = 2 x b) y = 4 x c) y = 3 x = 4 x 5 4 1 gradien t 1. Step off the gradient from the origin (0, 0) 2. Join the plotted point back to the origin To draw, always write gradients as fractions

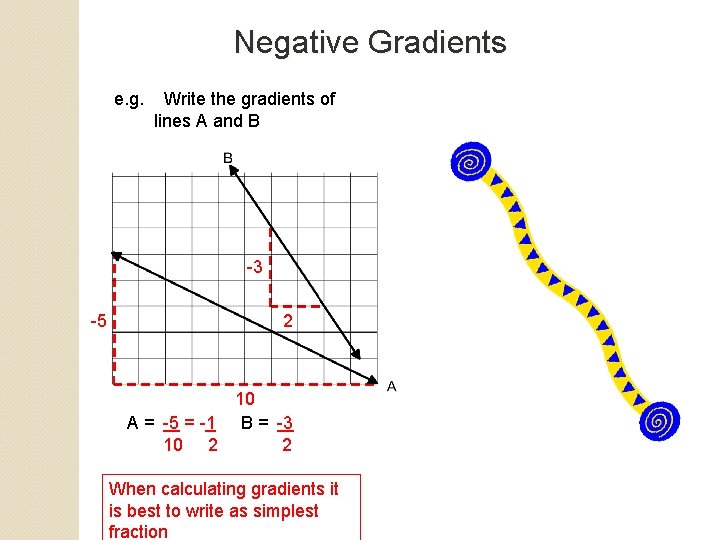
Negative Gradients e. g. Write the gradients of lines A and B -3 -5 2 10 A = -5 = -1 B = -3 10 2 2 When calculating gradients it is best to write as simplest fraction

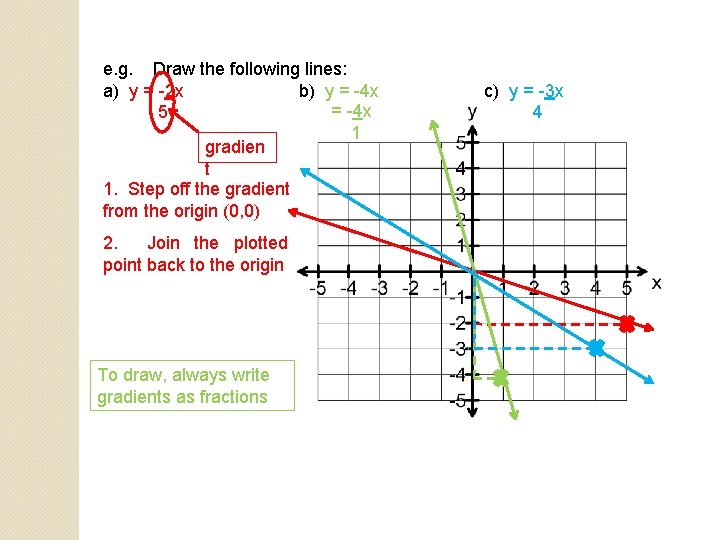
e. g. Draw the following lines: a) y = -2 x b) y = -4 x 5 1 gradien t 1. Step off the gradient from the origin (0, 0) 2. Join the plotted point back to the origin To draw, always write gradients as fractions c) y = -3 x 4

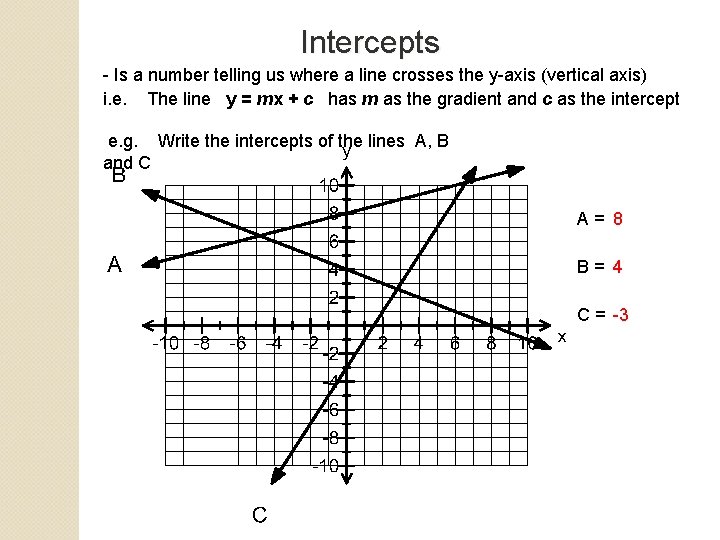
Intercepts - Is a number telling us where a line crosses the y-axis (vertical axis) i. e. The line y = mx + c has m as the gradient and c as the intercept e. g. Write the intercepts of the lines A, B and C A= 8 B= 4 C = -3

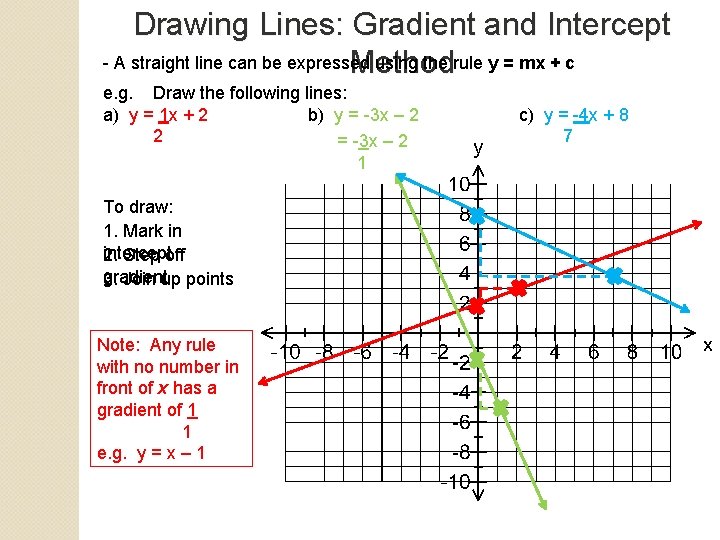
Drawing Lines: Gradient and Intercept - A straight line can be expressed using the rule y = mx + c Method e. g. Draw the following lines: a) y = 1 x + 2 b) y = -3 x – 2 2 = -3 x – 2 1 To draw: 1. Mark in intercept 2. Step off gradient 3. Join up points Note: Any rule with no number in front of x has a gradient of 1 1 e. g. y = x – 1 c) y = -4 x + 8 7

Writing Equations of Lines - A straight line can be expressed using the rule y = mx + c e. g. Write equations for the following lines 3 c = -6 4 y = 3 x – 6 4 A: m = -2 c = +1 3 y = -2 x + 1 3 B: m = 4 c =+4 1 y = 4 x + 4 1 C: m =

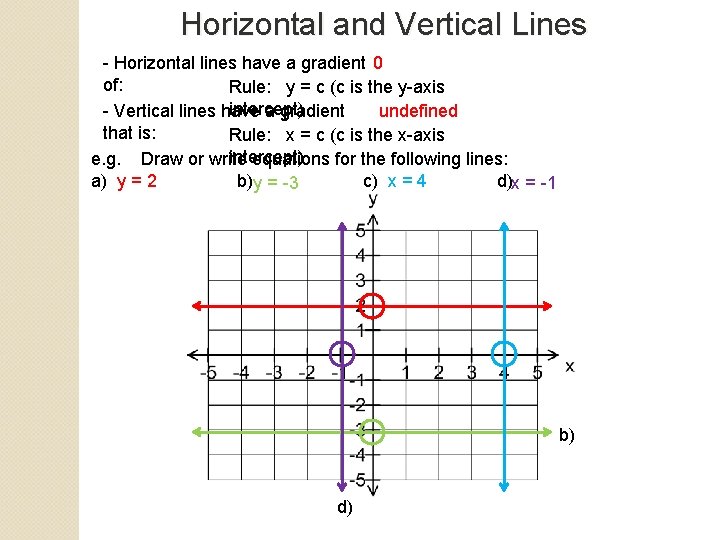
Horizontal and Vertical Lines - Horizontal lines have a gradient 0 of: Rule: y = c (c is the y-axis intercept) - Vertical lines have a gradient undefined that is: Rule: x = c (c is the x-axis intercept) e. g. Draw or write equations for the following lines: a) y = 2 b)y = -3 c) x = 4 d)x = -1 b) d)

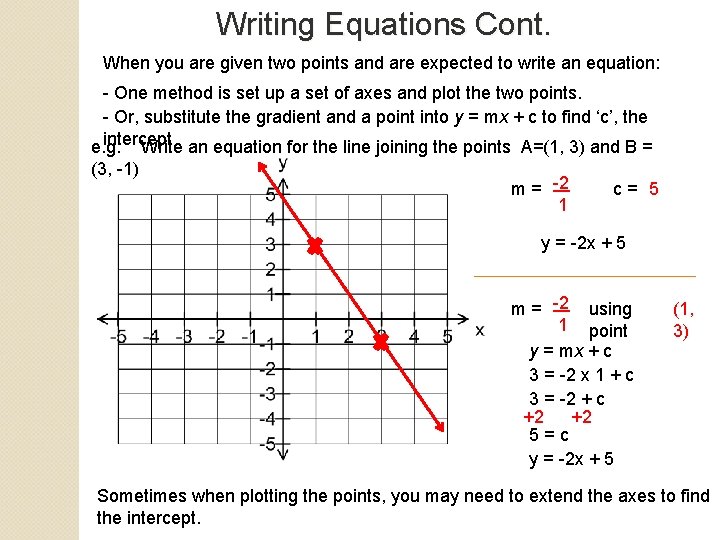
Writing Equations Cont. When you are given two points and are expected to write an equation: - One method is set up a set of axes and plot the two points. - Or, substitute the gradient and a point into y = mx + c to find ‘c’, the intercept e. g. Write an equation for the line joining the points A=(1, 3) and B = (3, -1) m = -2 1 c= 5 y = -2 x + 5 m = -2 using 1 point y = mx + c 3 = -2 x 1 + c 3 = -2 + c +2 +2 5=c y = -2 x + 5 (1, 3) Sometimes when plotting the points, you may need to extend the axes to find the intercept.

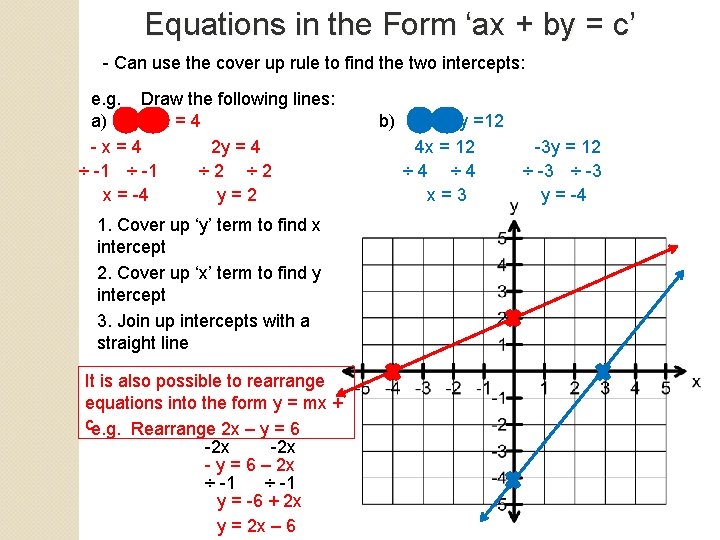
Equations in the Form ‘ax + by = c’ - Can use the cover up rule to find the two intercepts: e. g. Draw the following lines: a) 2 y – x = 4 -x=4 2 y = 4 ÷ -1 ÷ 2 x = -4 y=2 1. Cover up ‘y’ term to find x intercept 2. Cover up ‘x’ term to find y intercept 3. Join up intercepts with a straight line It is also possible to rearrange equations into the form y = mx + ce. g. Rearrange 2 x – y = 6 -2 x - y = 6 – 2 x ÷ -1 y = -6 + 2 x y = 2 x – 6 b) 4 x – 3 y =12 4 x = 12 ÷ 4 x=3 -3 y = 12 ÷ -3 y = -4

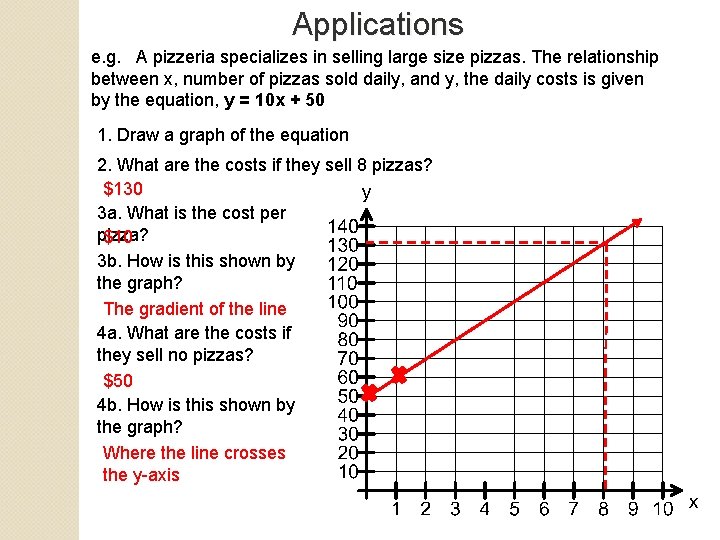
Applications e. g. A pizzeria specializes in selling large size pizzas. The relationship between x, number of pizzas sold daily, and y, the daily costs is given by the equation, y = 10 x + 50 1. Draw a graph of the equation 2. What are the costs if they sell 8 pizzas? $130 3 a. What is the cost per pizza? $10 3 b. How is this shown by the graph? The gradient of the line 4 a. What are the costs if they sell no pizzas? $50 4 b. How is this shown by the graph? Where the line crosses the y-axis

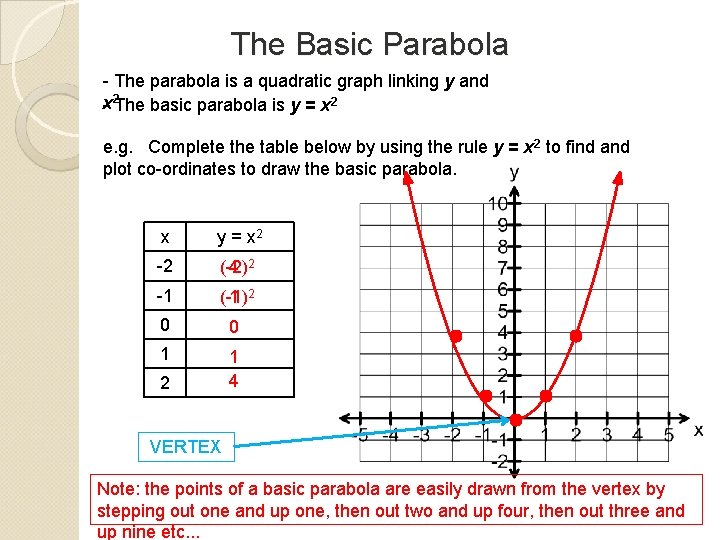
The Basic Parabola - The parabola is a quadratic graph linking y and -x 2 The basic parabola is y = x 2 e. g. Complete the table below by using the rule y = x 2 to find and plot co-ordinates to draw the basic parabola. x y = x 2 -2 (-2) 4 2 -1 (-1) 1 2 0 0 1 1 4 2 VERTEX Note: the points of a basic parabola are easily drawn from the vertex by stepping out one and up one, then out two and up four, then out three and up nine etc. . .

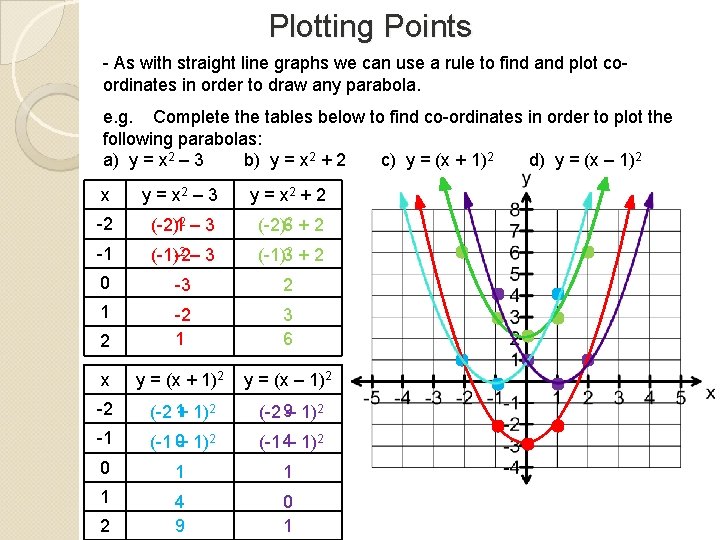
Plotting Points - As with straight line graphs we can use a rule to find and plot coordinates in order to draw any parabola. e. g. Complete the tables below to find co-ordinates in order to plot the following parabolas: a) y = x 2 – 3 b) y = x 2 + 2 c) y = (x + 1)2 d) y = (x – 1)2 x y = x 2 – 3 y = x 2 + 2 -2 (-2)12 – 3 (-2)62 + 2 -1 2 – 3 (-1)-2 (-1)32 + 2 0 -3 2 1 2 -2 1 3 6 x y = (x + 1)2 y = (x – 1)2 -2 (-2 1+ 1)2 (-2 9– 1)2 -1 (-1 0+ 1)2 (-1 4– 1)2 0 1 1 1 4 9 0 1 2

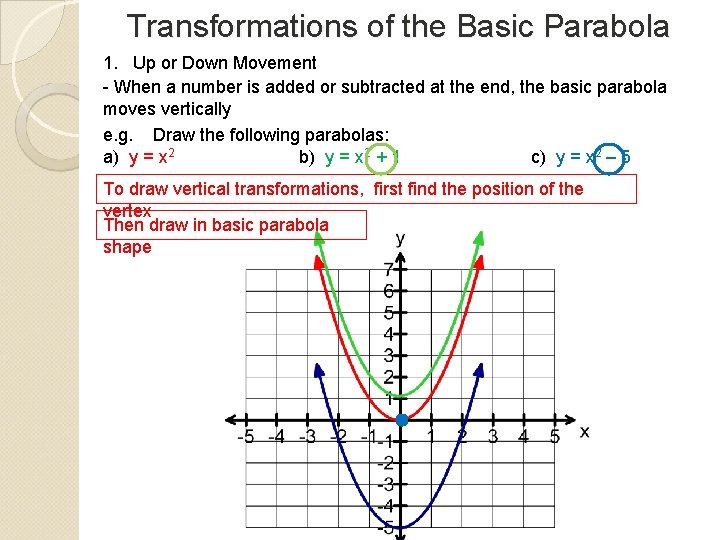
Transformations of the Basic Parabola 1. Up or Down Movement - When a number is added or subtracted at the end, the basic parabola moves vertically e. g. Draw the following parabolas: a) y = x 2 b) y = x 2 + 1 c) y = x 2 – 5 To draw vertical transformations, first find the position of the vertex Then draw in basic parabola shape

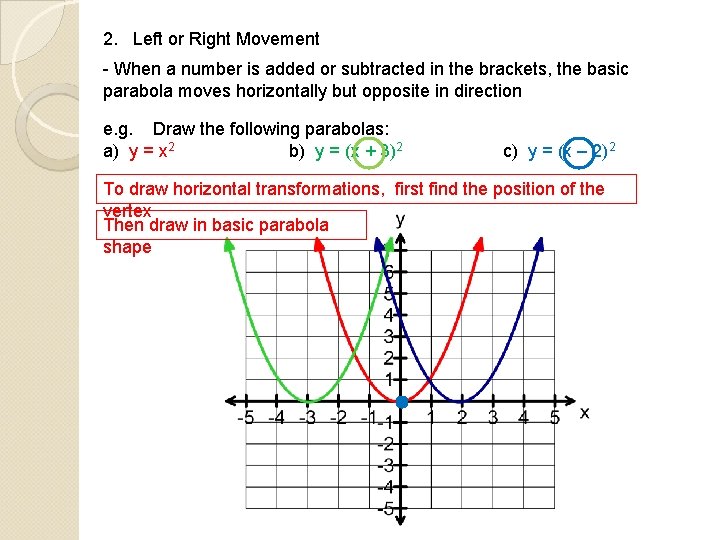
2. Left or Right Movement - When a number is added or subtracted in the brackets, the basic parabola moves horizontally but opposite in direction e. g. Draw the following parabolas: a) y = x 2 b) y = (x + 3)2 c) y = (x – 2)2 To draw horizontal transformations, first find the position of the vertex Then draw in basic parabola shape

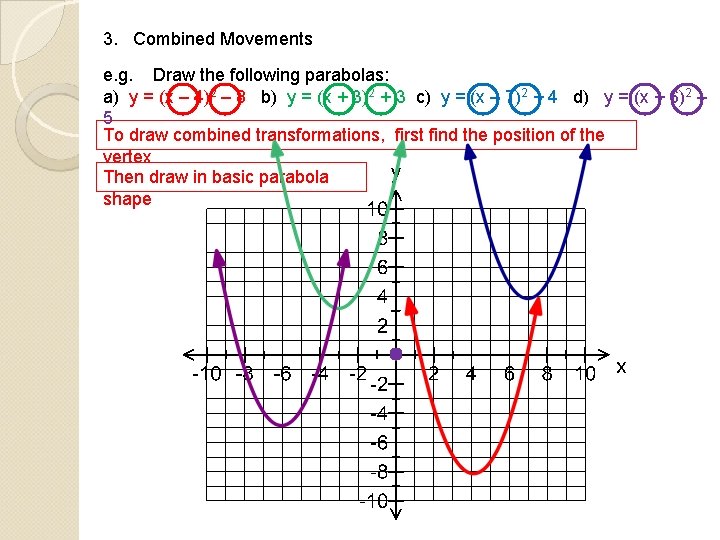
3. Combined Movements e. g. Draw the following parabolas: a) y = (x – 4)2 – 8 b) y = (x + 3)2 + 3 c) y = (x – 7)2 + 4 d) y = (x + 6)2 – 5 To draw combined transformations, first find the position of the vertex Then draw in basic parabola shape

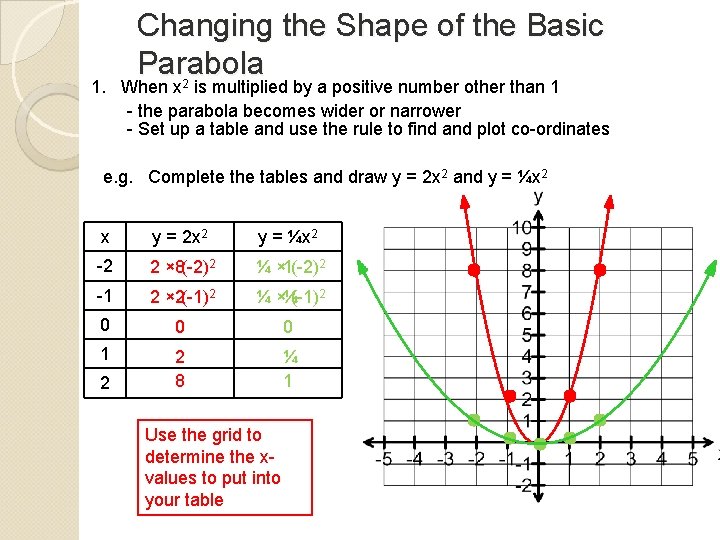
Changing the Shape of the Basic Parabola 1. When x 2 is multiplied by a positive number other than 1 - the parabola becomes wider or narrower - Set up a table and use the rule to find and plot co-ordinates e. g. Complete the tables and draw y = 2 x 2 and y = ¼x 2 x y = 2 x 2 y = ¼x 2 -2 2 × 8(-2)2 ¼ × 1(-2)2 -1 2 × 2(-1)2 ¼ ×¼(-1)2 0 0 0 1 2 8 ¼ 1 2 Use the grid to determine the xvalues to put into your table

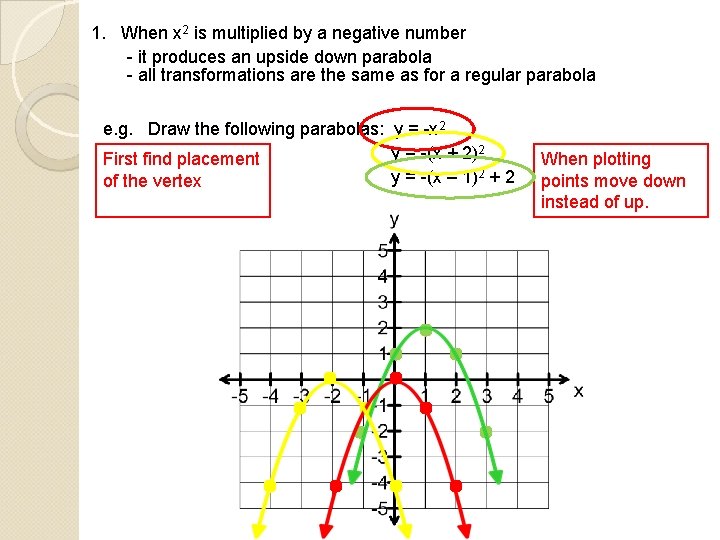
1. When x 2 is multiplied by a negative number - it produces an upside down parabola - all transformations are the same as for a regular parabola e. g. Draw the following parabolas: y = -x 2 y = -(x + 2)2 First find placement y = -(x – 1)2 + 2 of the vertex When plotting points move down instead of up.

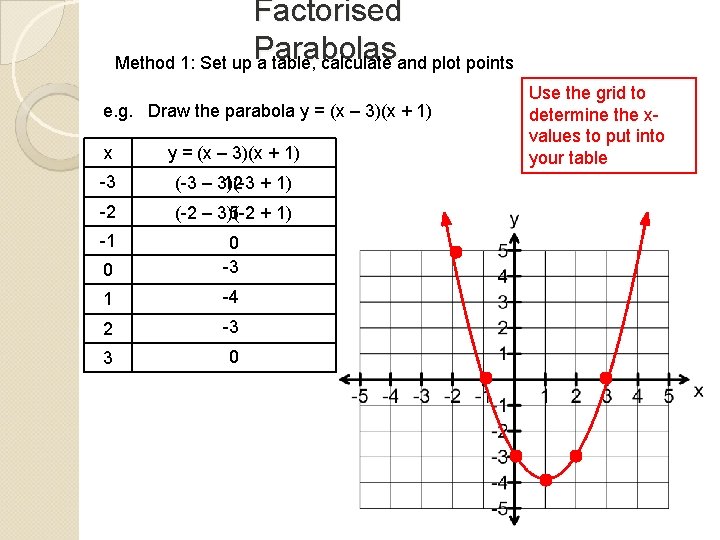
Factorised Parabolas Method 1: Set up a table, calculate and plot points e. g. Draw the parabola y = (x – 3)(x + 1) x y = (x – 3)(x + 1) -3 (-3 – 3)(-3 12 + 1) -2 (-2 – 3)(-2 5 + 1) -1 0 0 -3 1 -4 2 -3 3 0 Use the grid to determine the xvalues to put into your table

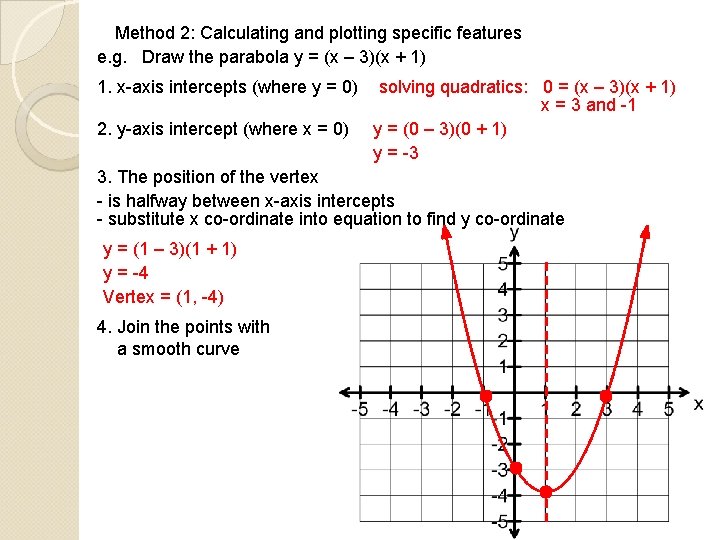
Method 2: Calculating and plotting specific features e. g. Draw the parabola y = (x – 3)(x + 1) 1. x-axis intercepts (where y = 0) 2. y-axis intercept (where x = 0) solving quadratics: 0 = (x – 3)(x + 1) x = 3 and -1 y = (0 – 3)(0 + 1) y = -3 3. The position of the vertex - is halfway between x-axis intercepts - substitute x co-ordinate into equation to find y co-ordinate y = (1 – 3)(1 + 1) y = -4 Vertex = (1, -4) 4. Join the points with a smooth curve

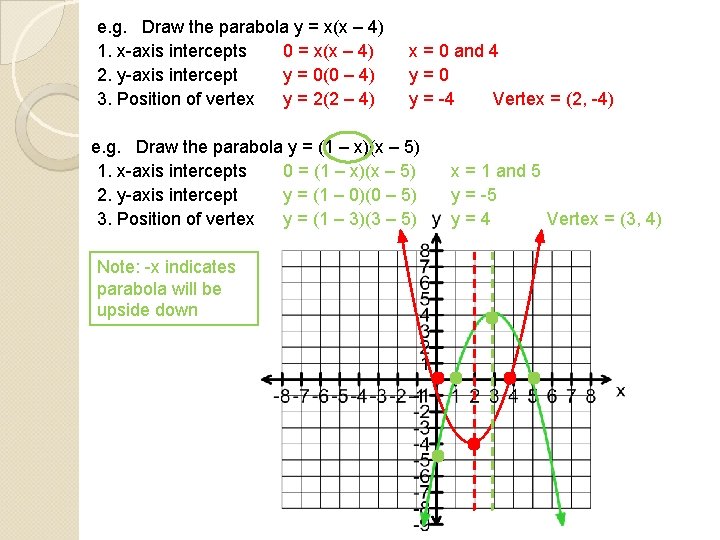
e. g. Draw the parabola y = x(x – 4) 1. x-axis intercepts 0 = x(x – 4) 2. y-axis intercept y = 0(0 – 4) 3. Position of vertex y = 2(2 – 4) x = 0 and 4 y=0 y = -4 Vertex = (2, -4) e. g. Draw the parabola y = (1 – x)(x – 5) 1. x-axis intercepts 0 = (1 – x)(x – 5) 2. y-axis intercept y = (1 – 0)(0 – 5) 3. Position of vertex y = (1 – 3)(3 – 5) Note: -x indicates parabola will be upside down x = 1 and 5 y = -5 y=4 Vertex = (3, 4)

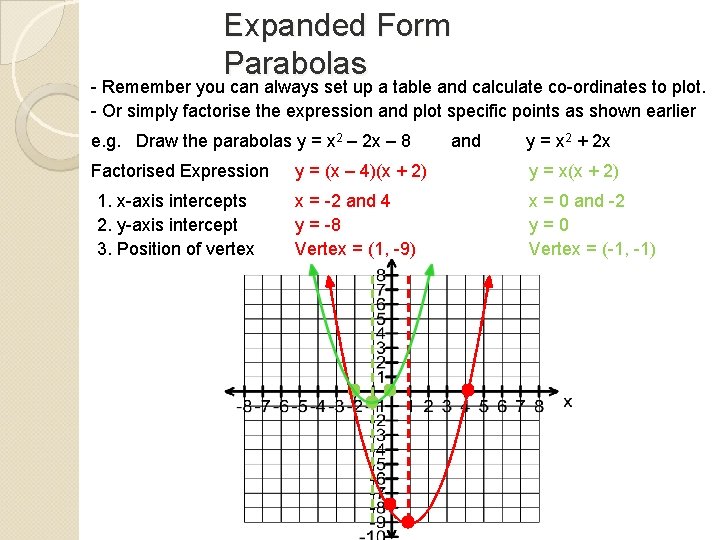
Expanded Form Parabolas - Remember you can always set up a table and calculate co-ordinates to plot. - Or simply factorise the expression and plot specific points as shown earlier e. g. Draw the parabolas y = x 2 – 2 x – 8 Factorised Expression 1. x-axis intercepts 2. y-axis intercept 3. Position of vertex and y = x 2 + 2 x y = (x – 4)(x + 2) y = x(x + 2) x = -2 and 4 y = -8 Vertex = (1, -9) x = 0 and -2 y=0 Vertex = (-1, -1)

Writing Equations - If the parabola intercepts x-axis, you can substitute into y = (x – a)(x – b) - Or, you can substitute the vertex co-ordinates into y = (x – a)2 + b e. g. Write equations for the following parabolas a) y = (x – 2)(x – 4) or Vertex = (3, -1) y = (x – 3)2 – 1 b) Vertex = (-2, 1) y = (x + 2)2 + 1 c) y = - (x + 1)(x + 5) or Vertex = (-3, 4) y = - (x + 3)2 + 4 Always substitute in the opposite sign x-value Add in a negative sign if parabola upside down

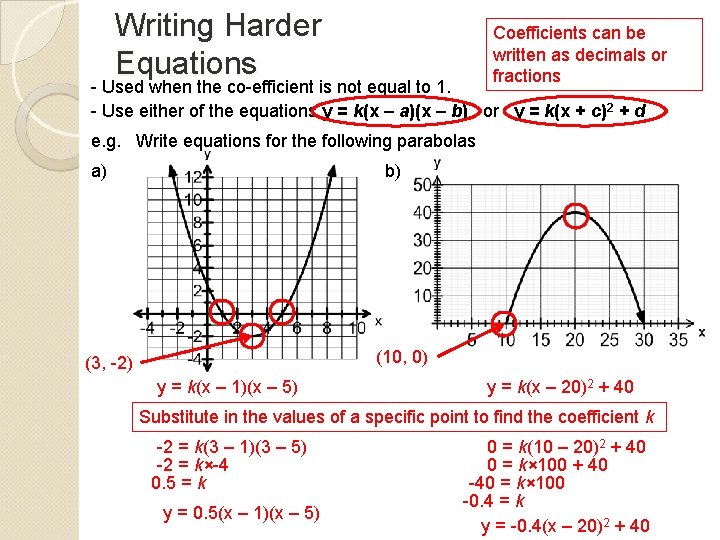
Writing Harder Equations Coefficients can be written as decimals or fractions - Used when the co-efficient is not equal to 1. - Use either of the equations y = k(x – a)(x – b) or y = k(x + c)2 + d e. g. Write equations for the following parabolas a) b) (10, 0) (3, -2) y = k(x – 1)(x – 5) y = k(x – 20)2 + 40 Substitute in the values of a specific point to find the coefficient k -2 = k(3 – 1)(3 – 5) -2 = k×-4 0. 5 = k y = 0. 5(x – 1)(x – 5) 0 = k(10 – 20)2 + 40 0 = k× 100 + 40 -40 = k× 100 -0. 4 = k y = -0. 4(x – 20)2 + 40