Table of Contents Chapter 6 Network Optimization Problems

Table of Contents Chapter 6 (Network Optimization Problems) Minimum-Cost Flow Problems (Section 6. 1) A Case Study: The BMZ Maximum Flow Problem (Section 6. 2) Maximum Flow Problems (Section 6. 3) Shortest Path Problems: Littletown Fire Department (Section 6. 4) Shortest Path Problems: General Characteristics (Section 6. 4) Shortest Path Problems: Minimizing Sarah’s Total Cost (Section 6. 4) Shortest Path Problems: Minimizing Quick’s Total Time (Section 6. 4) 6. 2– 6. 12 6. 13– 6. 16 6. 17– 6. 21 6. 22– 6. 25 6. 26– 6. 27 6. 28– 6. 31 6. 32– 6. 36 © 2014 by Mc. Graw-Hill Education. This is proprietary material solely for authorized instructor use. Not authorized for sale or distribution in any manner. This document may not be copied, scanned, duplicated, forwarded, distributed, or posted on a website, in whole or part.

Distribution Unlimited Co. Problem • The Distribution Unlimited Co. has two factories producing a product that needs to be shipped to two warehouses – – Factory 1 produces 80 units. Factory 2 produces 70 units. Warehouse 1 needs 60 units. Warehouse 2 needs 90 units. • There are rail links directly from Factory 1 to Warehouse 1 and Factory 2 to Warehouse 2. • Independent truckers are available to ship up to 50 units from each factory to the distribution center, and then 50 units from the distribution center to each warehouse. Question: How many units (truckloads) should be shipped along each shipping lane? 6 -2

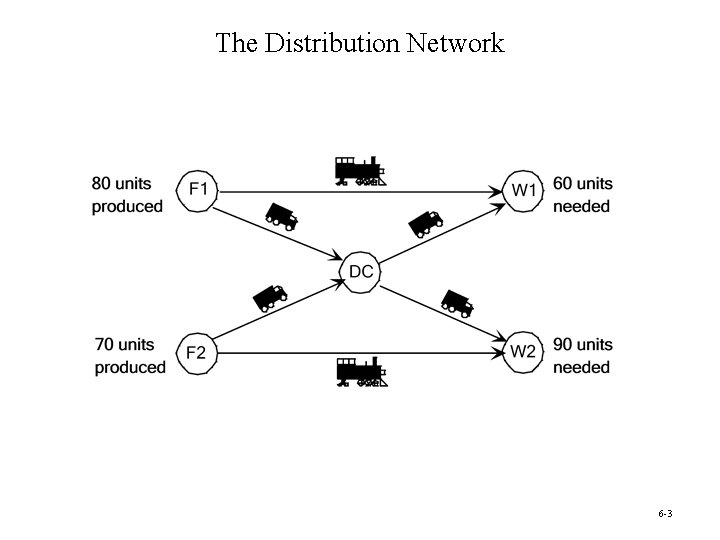
The Distribution Network 6 -3

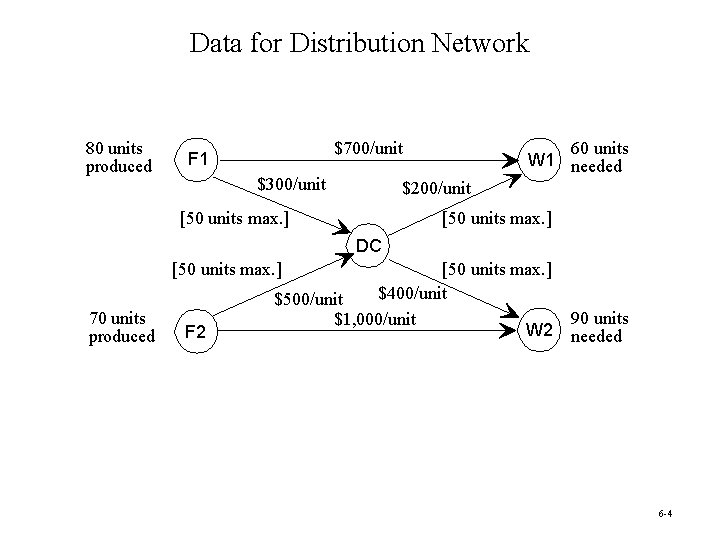
Data for Distribution Network 80 units produced $700/unit F 1 $300/unit 60 units W 1 needed $200/unit [50 units max. ] DC [50 units max. ] 70 units produced F 2 [50 units max. ] $400/unit $500/unit $1, 000/unit W 2 90 units needed 6 -4

A Network Model [80] [- 60] $700 F 1 $300 [50] [0] W 1 $200 [50] DC $500 [50] F 2 [70] $400 [50] $1, 000 W 2 [- 90] 6 -5

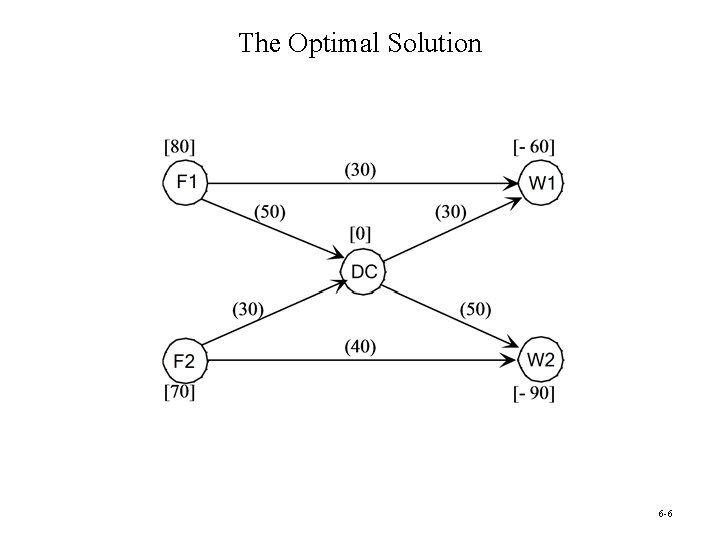
The Optimal Solution 6 -6

Terminology for Minimum-Cost Flow Problems 1. The model for any minimum-cost flow problem is represented by a network with flow passing through it. 2. The circles in the network are called nodes. 3. Each node where the net amount of flow generated (outflow minus inflow) is a fixed positive number is a supply node. 4. Each node where the net amount of flow generated is a fixed negative number is a demand node. 5. Any node where the net amount of flow generated is fixed at zero is a transshipment node. Having the amount of flow out of the node equal the amount of flow into the node is referred to as conservation of flow. 6. The arrows in the network are called arcs. 7. The maximum amount of flow allowed through an arc is referred to as the capacity of that arc. 6 -7

Assumptions of a Minimum-Cost Flow Problem 1. At least one of the nodes is a supply node. 2. At least one of the other nodes is a demand node. 3. All the remaining nodes are transshipment nodes. 4. Flow through an arc is only allowed in the direction indicated by the arrowhead, where the maximum amount of flow is given by the capacity of that arc. (If flow can occur in both directions, this would be represented by a pair of arcs pointing in opposite directions. ) 5. The network has enough arcs with sufficient capacity to enable all the flow generated at the supply nodes to reach all the demand nodes. 6. The cost of the flow through each arc is proportional to the amount of that flow, where the cost per unit flow is known. 7. The objective is to minimize the total cost of sending the available supply through the network to satisfy the given demand. (An alternative objective is to maximize the total profit from doing this. ) 6 -8

Properties of Minimum-Cost Flow Problems • The Feasible Solutions Property: Under the previous assumptions, a minimum-cost flow problem will have feasible solutions if and only if the sum of the supplies from its supply nodes equals the sum of the demands at its demand nodes. • The Integer Solutions Property: As long as all the supplies, demands, and arc capacities have integer values, any minimum-cost flow problem with feasible solutions is guaranteed to have an optimal solution with integer values for all its flow quantities. 6 -9

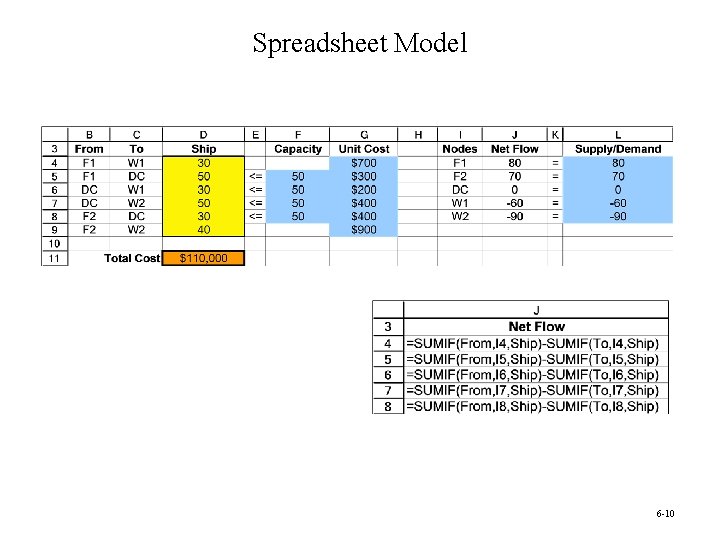
Spreadsheet Model 6 -10

The SUMIF Function • The SUMIF formula can be used to simplify the node flow constraints. =SUMIF(Range A, x, Range B) • For each quantity in (Range A) that equals x, SUMIF sums the corresponding entries in (Range B). • The net outflow (flow out – flow in) from node x is then =SUMIF(“From labels”, x, “Flow”) – SUMIF(“To labels”, x, “Flow”) 6 -11

Typical Applications of Minimum-Cost Flow Problems Kind of Application Supply Nodes Transshipment Nodes Demand Nodes Operation of a distribution network Sources of goods Intermediate storage facilities Customers Solid waste management Sources of solid waste Processing facilities Landfill locations Operation of a supply Vendors network Intermediate warehouses Processing facilities Coordinating product Plants mixes at plants Production of a specific product Market for a specific product Cash flow management Short-term investment options Needs for cash at a specific time Sources of cash at a specific time 6 -12

The BMZ Maximum Flow Problem • The BMZ Company is a European manufacturer of luxury automobiles. Its exports to the United States are particularly important. • BMZ cars are becoming especially popular in California, so it is particularly important to keep the Los Angeles center well supplied with replacement parts for repairing these cars. • BMZ needs to execute a plan quickly for shipping as much as possible from the main factory in Stuttgart, Germany to the distribution center in Los Angeles over the next month. • The limiting factor on how much can be shipped is the limited capacity of the company’s distribution network. Question: How many units should be sent through each shipping lane to maximize the total units flowing from Stuttgart to Los Angeles? 6 -13

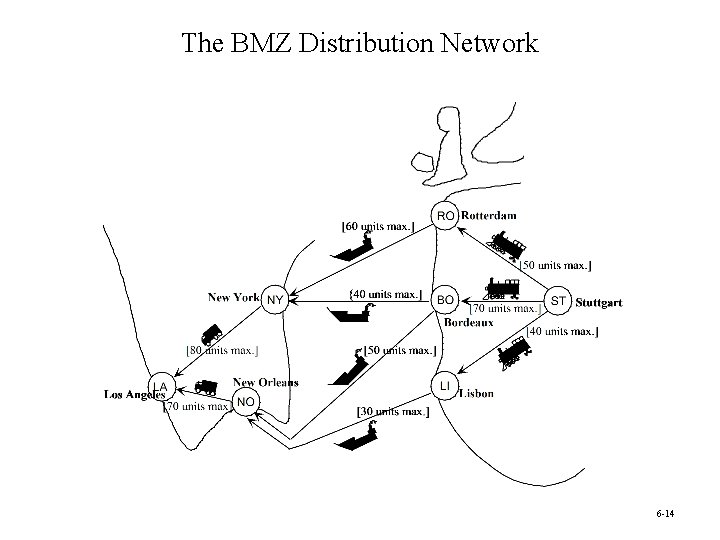
The BMZ Distribution Network 6 -14

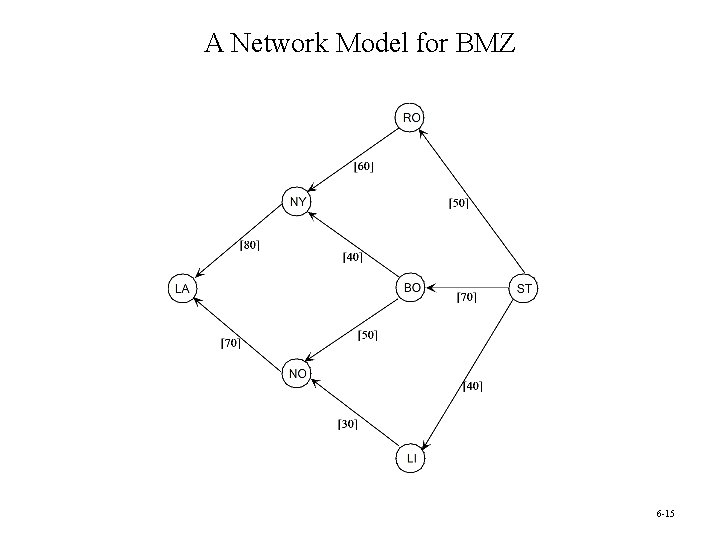
A Network Model for BMZ 6 -15

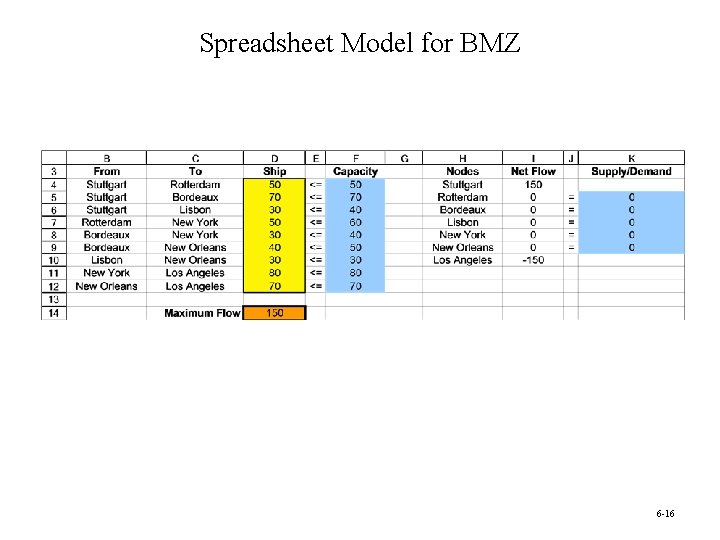
Spreadsheet Model for BMZ 6 -16

Assumptions of Maximum Flow Problems 1. All flow through the network originates at one node, called the source, and terminates at one other node, called the sink. (The source and sink in the BMZ problem are the factory and the distribution center, respectively. ) 2. All the remaining nodes are transshipment nodes. 3. Flow through an arc is only allowed in the direction indicated by the arrowhead, where the maximum amount of flow is given by the capacity of that arc. At the source, all arcs point away from the node. At the sink, all arcs point into the node. 4. The objective is to maximize the total amount of flow from the source to the sink. This amount is measured in either of two equivalent ways, namely, either the amount leaving the source or the amount entering the sink. 6 -17

BMZ with Multiple Supply and Demand Points • BMZ has a second, smaller factory in Berlin. • The distribution center in Seattle has the capability of supplying parts to the customers of the distribution center in Los Angeles when shortages occur at the latter center. Question: How many units should be sent through each shipping lane to maximize the total units flowing from Stuttgart and Berlin to Los Angeles and Seattle? 6 -18

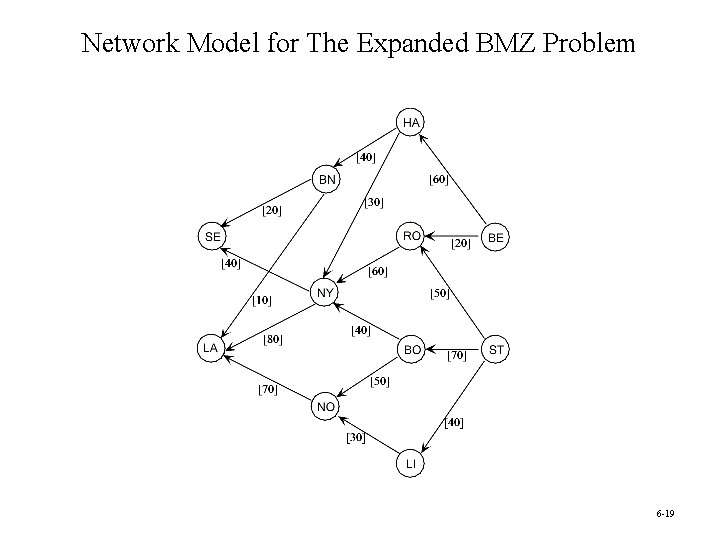
Network Model for The Expanded BMZ Problem 6 -19

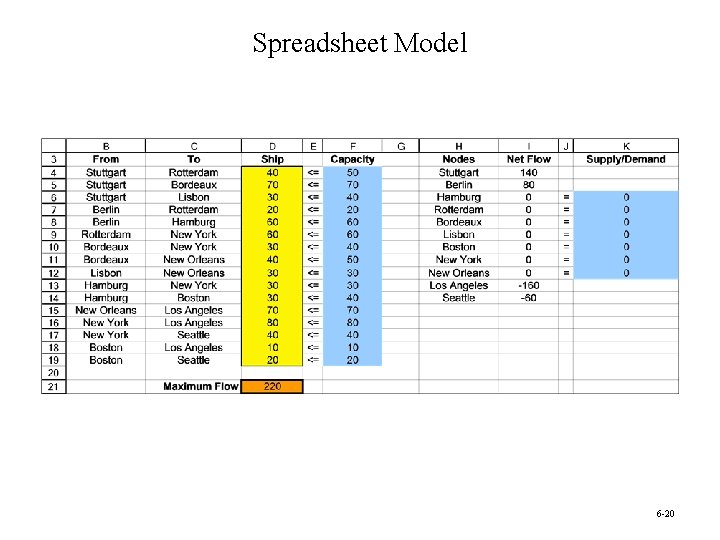
Spreadsheet Model 6 -20

Some Applications of Maximum Flow Problems 1. Maximize the flow through a distribution network, as for BMZ. 2. Maximize the flow through a company’s supply network from its vendors to its processing facilities. 3. Maximize the flow of oil through a system of pipelines. 4. Maximize the flow of water through a system of aqueducts. 5. Maximize the flow of vehicles through a transportation network. 6 -21

Littletown Fire Department • Littletown is a small town in a rural area. • Its fire department serves a relatively large geographical area that includes many farming communities. • Since there are numerous roads throughout the area, many possible routes may be available for traveling to any given farming community. Question: Which route from the fire station to a certain farming community minimizes the total number of miles? 6 -22

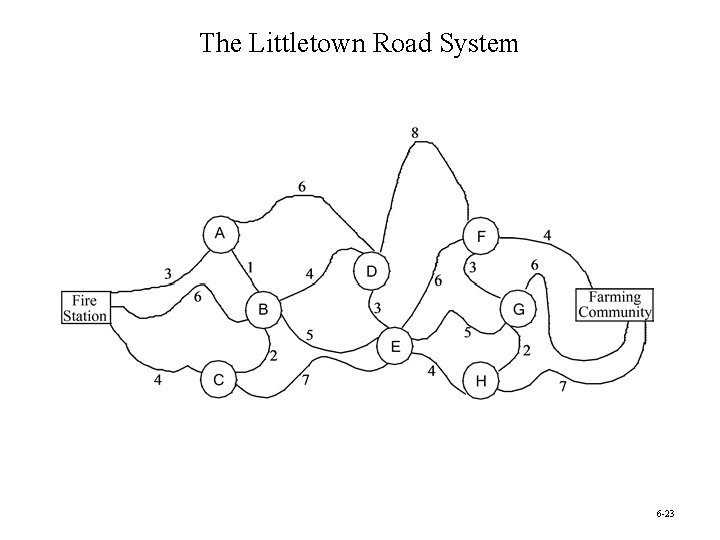
The Littletown Road System 6 -23

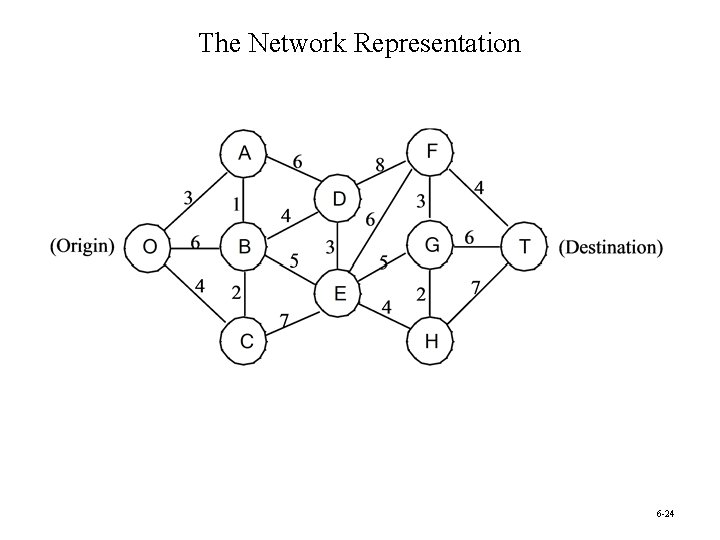
The Network Representation 6 -24

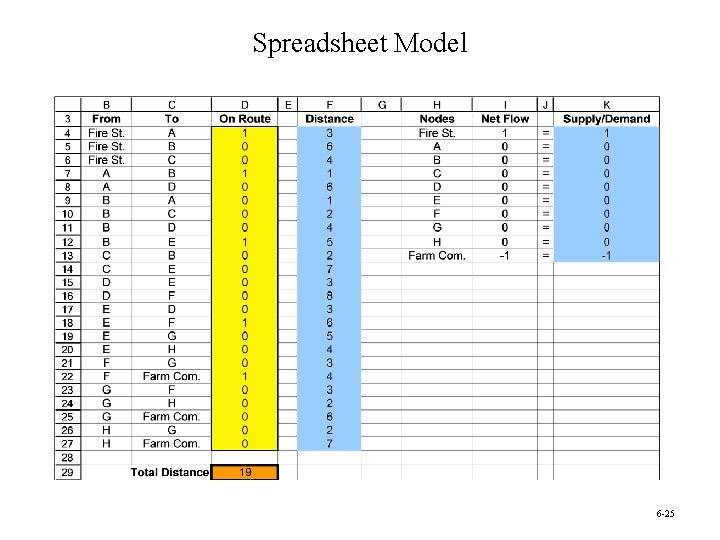
Spreadsheet Model 6 -25

Assumptions of a Shortest Path Problem 1. You need to choose a path through the network that starts at a certain node, called the origin, and ends at another certain node, called the destination. 2. The lines connecting certain pairs of nodes commonly are links (which allow travel in either direction), although arcs (which only permit travel in one direction) also are allowed. 3. Associated with each link (or arc) is a nonnegative number called its length. (Be aware that the drawing of each link in the network typically makes no effort to show its true length other than giving the correct number next to the link. ) 4. The objective is to find the shortest path (the path with the minimum total length) from the origin to the destination. 6 -26

Applications of Shortest Path Problems 1. Minimize the total distance traveled. 2. Minimize the total cost of a sequence of activities. 3. Minimize the total time of a sequence of activities. 6 -27

Minimizing Total Cost: Sarah’s Car Fund • Sarah has just graduated from high school. • As a graduation present, her parents have given her a car fund of $21, 000 to help purchase and maintain a three-year-old used car for college. • Since operating and maintenance costs go up rapidly as the car ages, Sarah may trade in her car on another three-year-old car one or more times during the next three summers if it will minimize her total net cost. (At the end of the four years of college, her parents will trade in the current used car on a new car for Sarah. ) Question: When should Sarah trade in her car (if at all) during the next three summers? 6 -28

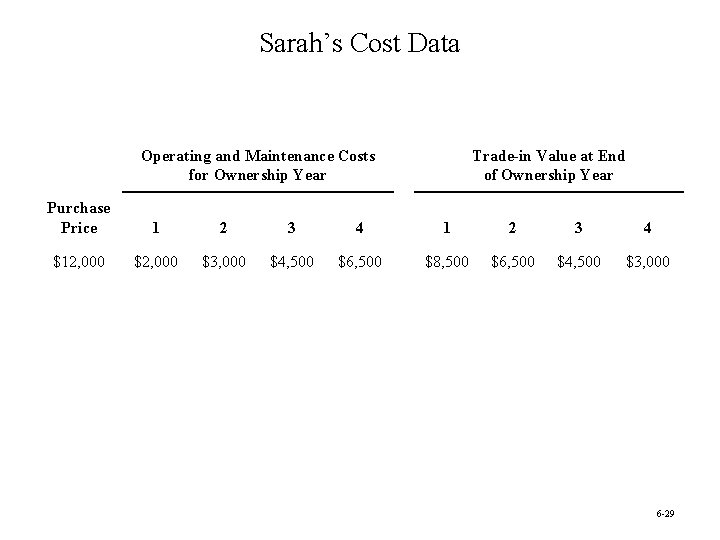
Sarah’s Cost Data Operating and Maintenance Costs for Ownership Year Trade-in Value at End of Ownership Year Purchase Price 1 2 3 4 $12, 000 $3, 000 $4, 500 $6, 500 $8, 500 $6, 500 $4, 500 $3, 000 6 -29

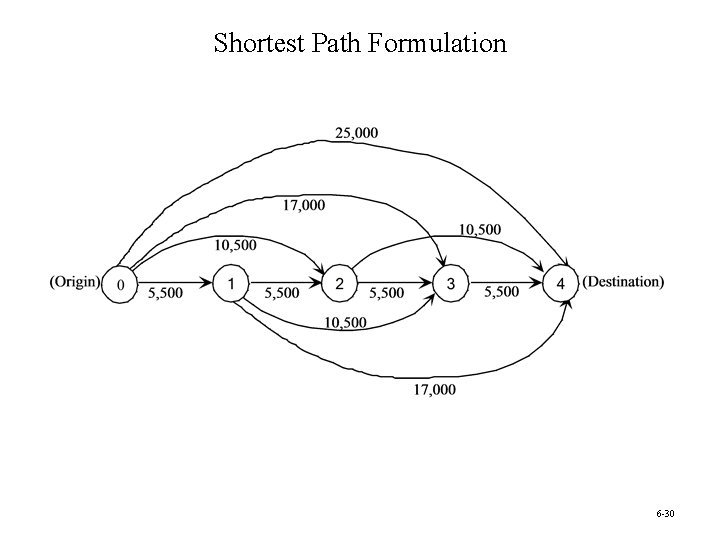
Shortest Path Formulation 6 -30

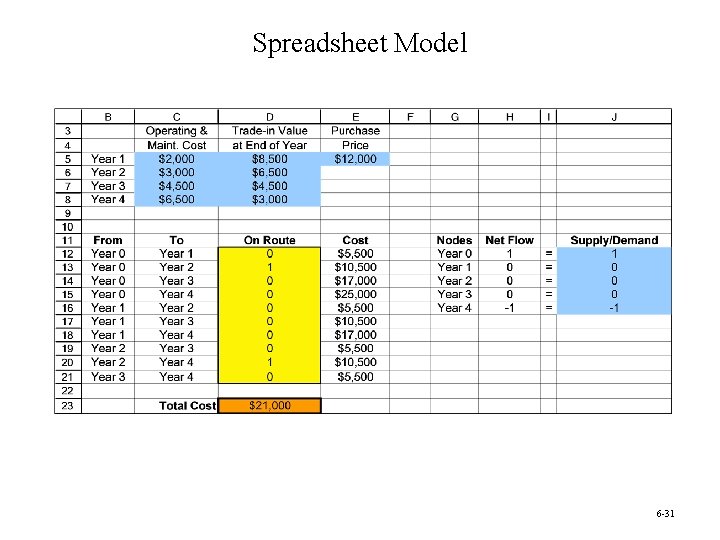
Spreadsheet Model 6 -31

Minimizing Total Time: Quick Company • The Quick Company has learned that a competitor is planning to come out with a new kind of product with great sales potential. • Quick has been working on a similar product that had been scheduled to come to market in 20 months. • Quick’s management wishes to rush the product out to meet the competition. • Each of four remaining phases can be conducted at a normal pace, at a priority pace, or at crash level to expedite completion. However, the normal pace has been ruled out as too slow for the last three phases. • $30 million is available for all four phases. Question: At what pace should each of the four phases be conducted? 6 -32

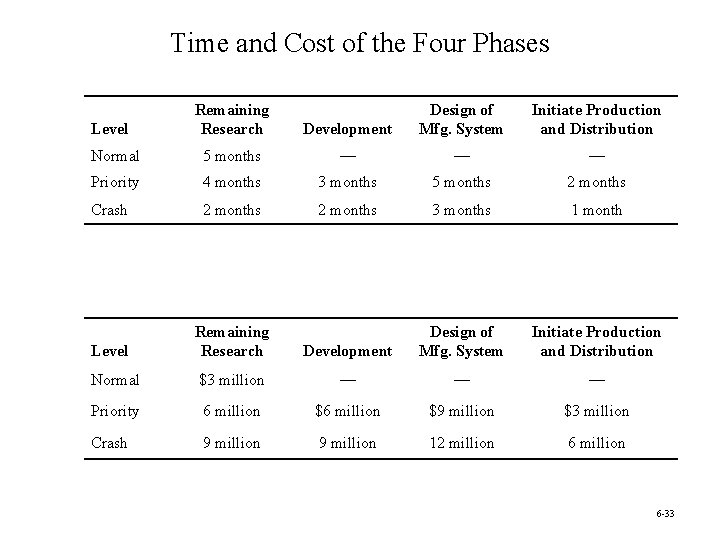
Time and Cost of the Four Phases Remaining Research Development Design of Mfg. System Initiate Production and Distribution Normal 5 months — — — Priority 4 months 3 months 5 months 2 months Crash 2 months 3 months 1 month Level Remaining Research Development Design of Mfg. System Initiate Production and Distribution Normal $3 million — — — Priority 6 million $9 million $3 million Crash 9 million 12 million 6 million Level 6 -33

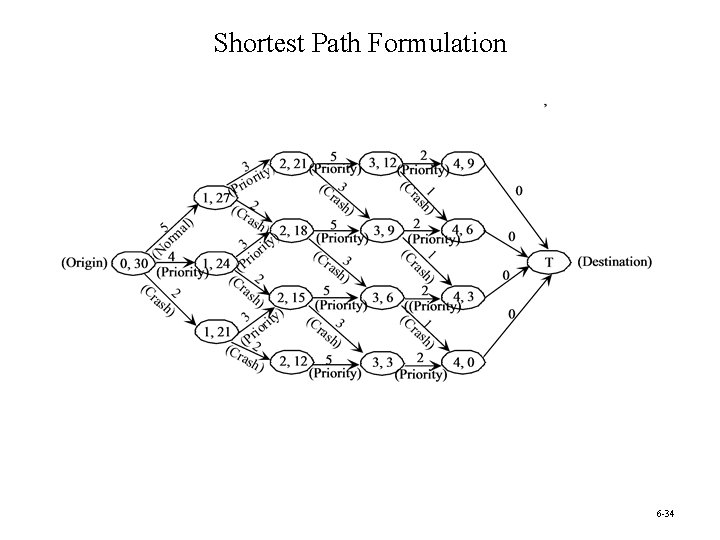
Shortest Path Formulation 6 -34

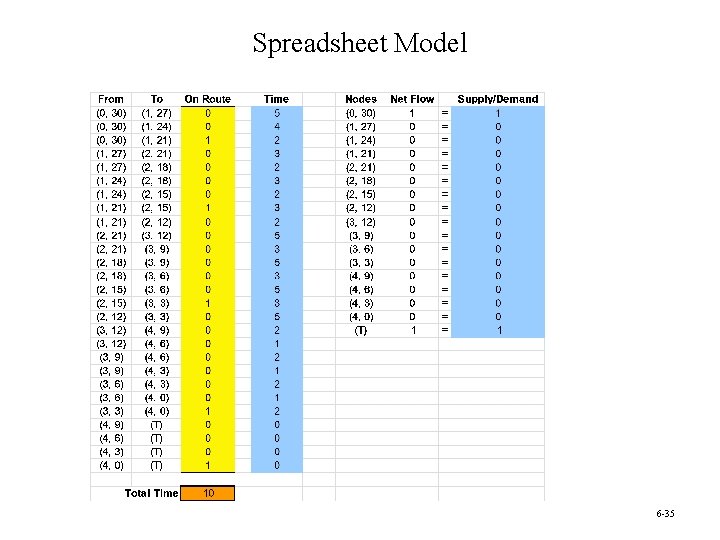
Spreadsheet Model 6 -35

The Optimal Solution Phase Level Time Cost Remaining research Crash 2 months $9 million Priority 3 months 6 million Crash 3 months 12 million Priority 2 months 3 million 10 months $30 million Development Design of manufacturing system Initiate production and distribution Total 6 -36