Table 2 1c and bent about their minor

Table 2. 1(c), and bent about their minor axis; solid round and square bars; solid rectangular sections bent about their minor axis: F b = 0. 72 F y …………… 3. 19 R R 3. 2. 6. 5. 3 Tension and compression on extreme fibers of rectangular tubular sections meeting the compact section requirements of Table 3. 1(b), and bent about their minor axis: F b = 0. 64 F y ……………. … 3. 20 R R 3. 2. 6. 5. 4 Tension and compression on extreme fibers of box-type flexural members meeting the “non-compact” section requirements of Table 3. 1(b): Fb = 0. 58 ……………. ……. R Fy R R R 3. 21 3. 2. 6. 5. 5 On extreme fibers of flexural members not covered by Clauses 3. 2. 6. 5. 1 – 3. 2. 6. 5. 4 : 1 - Tension F bt R F bt = 0. 58 ………………. . . R F y 3. 22 R R R Hence, F bt is taken as follows: R R Grade of Steel St 37 St 44 St 52 Fbt (t/cm 2) R t � 40 mm 1. 4 1. 6 2. 1 R P P 40 mm < t 1. 3 1. 5 2. 0 2 Compression F bc R I. When the compression flange is braced laterally at intervals exceeding L u as defined by Equations 3. 17 or 3. 18, the allowable bending stress in compression F bc will be taken as the larger value from Equations 3. 23 and 3. 24 or 3. 25) with a maximum value of 0. 58 F y : R R R

i- For shallow thick flanged sections, for any value of L/r T , the lateral torsional buckling stress is governed by the torsional strength given by: R R 800 C b 0. 58 Fy ………. 3. 23 Lu. d / Af Fltb 1 ii- For deep thin flanged sections, the lateral torsional buckling stress is governed by the buckling strength given by: a- When 84 Cb C Lu / r. T 188 b , then : Fy Fy Fltb 2 (0. 64 b- When L u / r. T 188 Fltb 2 (L u / r. T ) 2 Fy 1. 176 x 105 C b )Fy 0. 58 Fy ……. . 3. 24 Cb , then: Fy 12000 C 0. 58 Fy …………. . . …… 3. 25 (L u / r. T ) 2 b Alternatively, the lateral torsional buckling stress can be computed more accurately as the resultant of the above mentioned two components as: Fltb 2 1 Fltb 2 2 0. 58 F y …………… 3. 26 In the above Equations: Lu = Effective laterally unsupported length of compression flange = K. (distance between cross sections braced against twist, or lateral displacement of the compression flange in cm). K = Effective length factor (as given in Chapter 4 of Code) r T = Radius of gyration about minor axis of a section comprising the compression flange plus one third of compression web area (in cms) A f = (b f * t f ) Area of compression flange (in cm 2) R R R

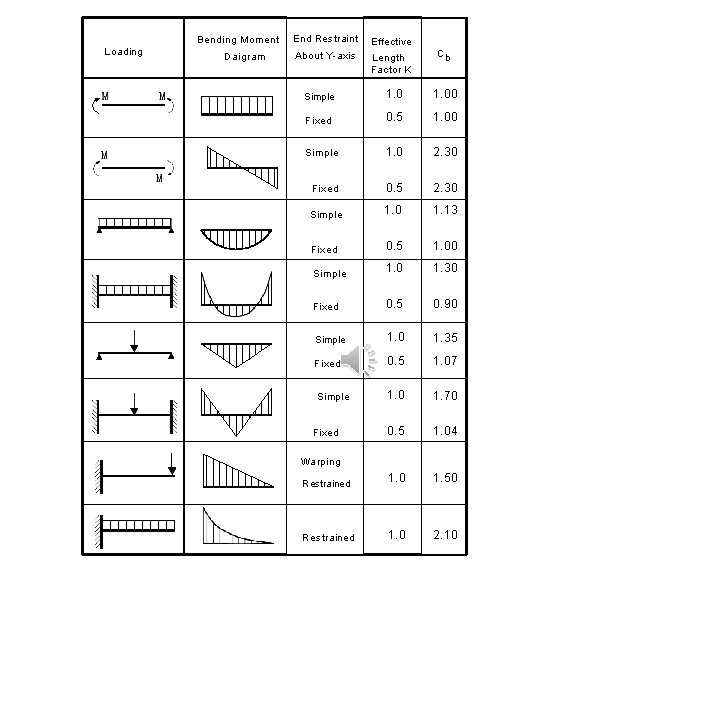
D = Depth of web (in cm) 2 Fy = Yield stress (t/cm ) t f = Compression flange thickness (in cm) P P R C b = Coefficient depending on the type of load and support conditions as given in Table 3. 2. For cases of unequal end moments without transverse loads, (C b ) can be computed from the expression : R R R C b = 1. 75 + 1. 05 (M 1 /M 2 ) + 0. 3 (M 1 /M 2 )2 ………………. . . R R R M 1 R R R 2. 3 3. 27 M 2 Where: (M 1 /M 2 ) is the algebraic ratio of the smaller to the larger end moments taken as positive for reverse curvature bending. When the bending moment at any point within the un-braced length is larger than the values at both ends of this length, the value of (C b) shall be taken as unity. R R R II- Compression on extreme fibres of channels bent about their major axis and meeting the requirements of Table 3. 1. Fltb 800 (L u. d / A f ) C b 0. 58 F y . … 3. 28 III. Slender sections which do not meet the non-compact section requirements of Table 3. 1 shall be designed using the same allowable stresses used for noncompact sections except that the section properties used in the design shall be based on the effective widths b e of compression elements as specified in Table 3. 3 for stiffened elements and Table 3. 4 for unstiffened elements. The effective R R width is calculated using a reduction factor ρ as b e = ρ b R R Where: 2 ρ = ( 0. 15 0. 05 ) / p 1 p and ……………. . . …… 3. 29 = normalized plate slenderness given by p p b/t 44 F y K …………… 3. 30

K = Plate buckling factor which depends on the stress ratio ψ as shown in Tables 3. 3 and 3. 4. b = Appropriate width, (see Table 3. 1) as follows : R b = d for webs b = = = b b t b for internal flange elements (except rectangle hollow sections) b-3 t for flanges of rectangle hollow sections. c for outstand flanges b for equal leg angles b or (b+h)/2 for unequal leg angles relevant thickness. Table (3. 2) Values of Coefficients K and C b R

Bending Moment Loading Daigram End Restraint Effective About Y-axis Length Factor K Cb Simple 1. 00 Fixed 0. 5 1. 00 Simple 1. 0 2. 30 Fixed 0. 5 2. 30 Simple 1. 0 1. 13 Fixed 0. 5 1. 00 Simple 1. 0 1. 30 Fixed 0. 5 0. 90 Simple 1. 0 1. 35 Fixed 0. 5 1. 07 Simple 1. 0 1. 70 0. 5 1. 04 1. 0 1. 50 1. 0 2. 10 Fixed Warping Restrained

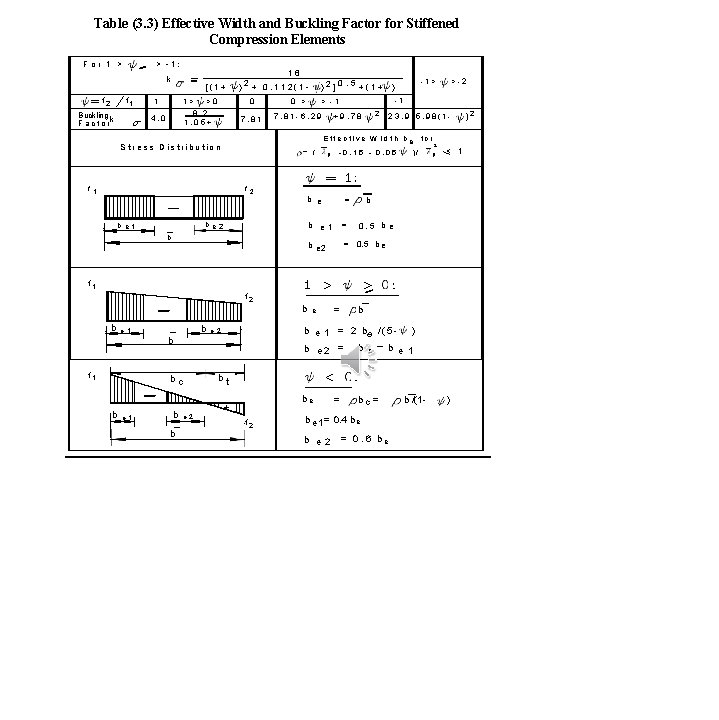
Table (3. 3) Effective Width and Buckling Factor for Stiffened Compression Elements For 1 > > -1: k f 2 f 1 Buckling k Factor [(1+ 1 0 1> >0 8. 2 1. 05+ 4. 0 16 2 ) + 0. 112(1 - 7. 81 2 +9. 78 = ( f 1 f 2 b e 2 b p >-2 -1 > -1 7. 81 -6. 29 -1> ) 23. 9 5. 98(1 - Effective W i d t h be Stress Distribution b e 1 0 > )2 ] 0. 5 +(1+ -0. 15 - 0. 05 b e = b e 1 = b e 2 = 0. 5 b e for )/ 2 p < 1 b 0. 5 b e f 1 f 2 b e 1 f 1 b b e 2 b b e 1 = 2 b e 2 b bc = /(5 - b e 2 = b e be bc = ) b e 1 bt + f 2 = b e 1 = 0. 4 b e 2 = 0. 6 be b /(1 - ) )2

Table (3. 4) Effective Width and Buckling Factor For Unstiffened Compression Elements Effective Width be Stress Distribution 1> 1 B u c k l i n g factor = p -0. 15 -0. 05 0 >0 0. 578 + 0. 34 0. 43 k ( 1. 70 c 0 > 1. 7 -5 for ) / 2 < 1 p >-1 +17. 1 > 0: 1 > be be b bc be t c B u c k l i n g factor k 0. 43 0. 57 0. 85 be 1 > 0. 57 -0. 21 + 0. 0 7 > 0: c bc be be c 3. 2. 6. 6 Allowable Crippling Stress in Web Fcrp Web crippling is a localised yielding that arises from high compressive stresses occurring in the vicinity of heavy concentrated loads. On the web of rolled shapes or built-up I-sections, at the toe of the fillet, the allowable crippling stress shall not exceed: -1 23. 8

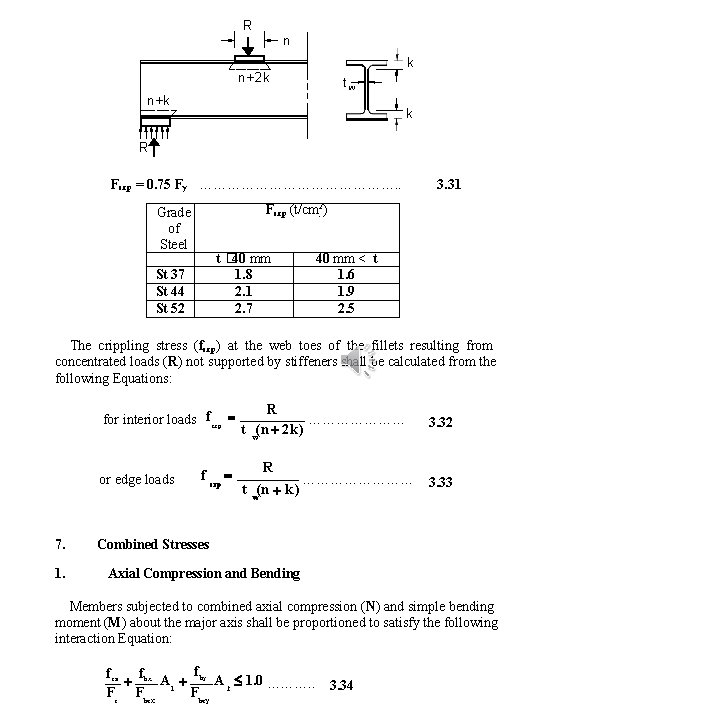
R n k n+2 k tw n+k k R Fcrp = 0. 75 Fy …………………. . 3. 31 Fcrp (t/cm 2) Grade of Steel P t � 40 mm 1. 8 2. 1 2. 7 St 37 St 44 St 52 P 40 mm < t 1. 6 1. 9 2. 5 The crippling stress (fcrp) at the web toes of the fillets resulting from concentrated loads (R) not supported by stiffeners shall be calculated from the following Equations: for interior loads f crp or edge loads 7. 1. f crp R ………………… t w(n 2 k) 3. 32 R ………… 3. 33 t w(n k) Combined Stresses Axial Compression and Bending Members subjected to combined axial compression (N) and simple bending moment (M) about the major axis shall be proportioned to satisfy the following interaction Equation: f f ca f bx A 1 by A 2 1. 0 ………. . Fc Fbcx Fbcy 3. 34

For cases when fca/ Fc < 0. 15, A 1 = A 2 = 1. 0. otherwise: C my C mx A A 1 2 , f f (1 ca ) FEy FEx fca Fc fbx, fby Fbcx, Fbcy FEx, FEy = Actual compressive stress due to axial compression. = The allowable compressive stress, as-appropriate, prescribed in Clause 3. 2. 6. 4. = The actual bending stresses based on moments about the x and y axes respectively. = The allowable compressive bending stresses for the x and y axes respectively, considering the member loaded in bending only as prescribed in Clause 3. 2. 6. 5. = The Euler stress divided by the factor of safety for buckling in the x and y directions respectively (t/cm 2). P FEx 7500 2 x , FEy 75 00 2 y P ……………. . 3. 35 Cm = Moment modification factor, and to be taken according to the following: a. For frames prevented from sway without transverse loading between supports Cm = 0. 6 - 0. 4 (M 1/ M 2) > 0. 4 where the end moments M 1 and M 2 carry a sign in accordance with end rotational direction; i. e. positive moment ratio for reverse curvature and negative moment ratio for single curvature (M 2 > M 1). b. For frames, prevented from sway, with transverse lateral loading between supports, Cm may be taken: i- For members with moment restraint at the ends Cm = 0. 85. ii- For members with simply supported end Cm = 1. 0. c. For frames permitted to sway, Cm= 0. 85.

d- In addition, sections at critical locations, e. g. at member ends, shall satisfy the following Equation: f f ca bx by 1. 0 …………………. . . ………… F F F 3. 36 c bcx bcy f 3. 2. 6. 7. 2 Axial Tension and Bending Members subjected to combined axial tension "N" and bending moment "M" shall be proportioned to satisfy the following conditions: f. N + f. M 0. 58 Fy …………………. 3. 37 Where: f. N = the tensile stress due to the axial tensile force (N)=N/Anet f. M = the maximum tensile stress due to the bending moment (M). In addition, the compressive bending stress alone shall be checked against the lateral torsional buckling stress. 3. 2. 6. 8 Equivalent Stress fe Whenever the material is subjected to axial and shear stresses, the equivalent stress (fe) must not exceed the permitted stresses given in this code plus 10%, and the equivalent stress shall be calculated as follows: f 7. e f 2 3 q 2 1. 1 F ……………… all 3. 38 ALLOWABLE STRESSES IN BEARINGS AND HINGES 1. Table 3. 5 gives the allowable stresses in (t/cm 2) in the parts of bearings and hinges made of cast iron, cast steel, and forged steel subject to bending or compression. P P These allowable stresses may be exceeded by 20% when the maximum combination of primary and additional stresses is taken into account.

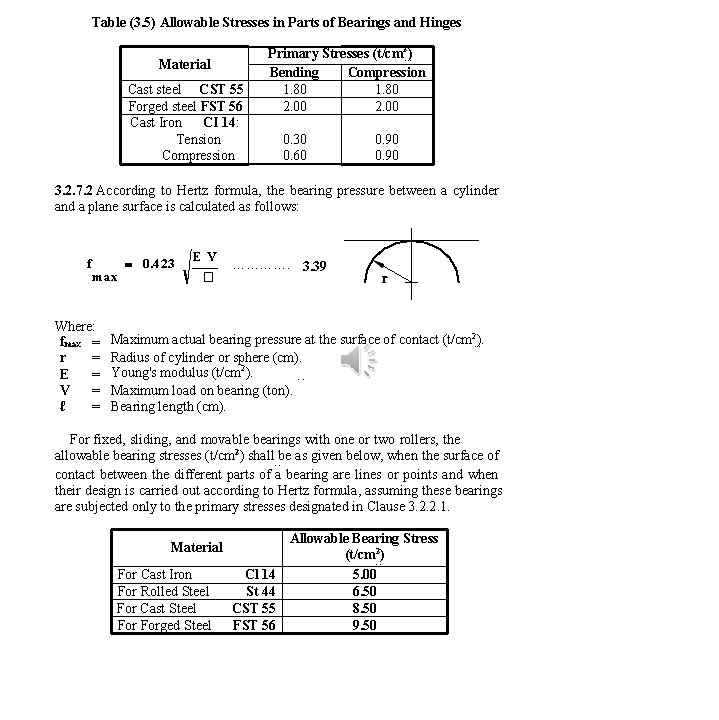
Table (3. 5) Allowable Stresses in Parts of Bearings and Hinges Material Primary Stresses (t/cm 2) Bending Compression 1. 80 2. 00 P 2 B Cast steel CST 55 Forged steel FST 56 Cast Iron CI 14: Tension Compression P 4 B 0. 30 0. 60 0. 90 3. 2. 7. 2 According to Hertz formula, the bearing pressure between a cylinder and a plane surface is calculated as follows: f max Where: fmax = r = E = V = ℓ = 0. 423 EV � …………. 3. 39 Maximum actual bearing pressure at the surface of contact (t/cm 2). Radius of cylinder or sphere (cm). Young's modulus (t/cm 2). Maximum load on bearing (ton). Bearing length (cm). P P For fixed, sliding, and movable bearings with one or two rollers, the allowable bearing stresses (t/cm 2) shall be as given below, when the surface of contact between the different parts of a bearing are lines or points and when their design is carried out according to Hertz formula, assuming these bearings are subjected only to the primary stresses designated in Clause 3. 2. 2. 1. P Material 5 B P Allowable Bearing Stress (t/cm 2) 5. 00 6. 50 8. 50 9. 50 P For Cast Iron For Rolled Steel For Cast Steel Forged Steel Cl 14 St 44 CST 55 FST 56 P

3. 2. 7. 3 The allowable load V (ton) on a cylindrical expansion roller shall not exceed the following values: Material Allowable Reaction (ton) Rolled steel St 37 Rolled steel St 44 Cast steel CST 55 Forged steel FST 56 0. 040 0. 055 0. 095 0. 117 d. ℓ Where: d ℓ = Diameter of roller (cm). = Length of roller (cm). In the case of movable bearings with more than two rollers, where the compressive force affecting the said rollers cannot be equally shared by all their parts, the aforesaid allowable reactions shall be increased by 20%. 3. 2. 7. 4 When bearings are provided with cylindrical cast steel knuckle pins, the diameter (d) of the pins shall be given by the formula: d 4 V. ……………… 3 � 3. 40 Where: d = Diameter of pin (cm). V = Vertical load (ton). ℓ = Length of pin (cm). The bearing pressure between pins made of cast or forged steel and the gusset plates shall not exceed 2. 40 t/cm 2. P P

3. FATIGUE 1. General A bridge member may respond to applied loads in one of the following three ways, see Fig 3. 1: (a) deform elastically, or (b) deform plastically, or (c) break. Since steel is a ductile material, failure of steel members is normally preceded by a considerable amount of elastic or plastic deformations. This amount depends on the magnitude of applied loads (below or above the yield level) and on the repetitive and cyclic nature of the load. Elastic Yield Failure Fig. 3. 1 Behaviour Stages: (a) Elastic, (b) Plastic, (c) Failure Sometimes, however, certain types of steel members may fail suddenly in the form of brittle fracture. It was found that this failure mode starts from the presence of very small defect and cracks in the member during fabrication due to rolling, cutting, drilling, and or welding, see Fig. 3. 2. The presence of these defects causes stress concentration around them as shown in Fig. 3. 3 a for a plate with a hole and in Fig. 3. 3 b at a fillet weld toe. The stress concentration around the defects causes them, although initially undetected, to increase in size and eventually propagate to failure when the member is subjected to a large number of stress cycles, see Fig 3. 4. In order to determine the design parameters that can prevent the occurrence of this brittle failure, Fracture Mechanics concepts can be applied to arrive at the fatigue strength of different bridge components; e. g. , members and connections. Control of fatigue failure is then achieved through efficient design and detailing.