TA Maths Course Session 1 Addition Subtraction Aims

TA Maths Course Session 1: Addition & Subtraction

Aims of the session: • To build understanding of mathematics and its development throughout KS 2 • To have a stronger awareness of how to support struggling learners and stretch those who are secure • To enhance subject knowledge of the pedagogical approaches to teaching mathematics

Language Addition • Addend + addend = sum Subtraction • Minuend – subtrahend = difference

Models of Addition Make up a word problem on a slip of paper that represents the calculation 12 + 3 = 15 • There are 12 girls and 3 boys. How many children altogether? • The chocolate bar was 12 p last week, but today the price went up by 3 p. What is the price now?

Building the Journey Year 3 Addition and Subtraction up to 3 digits using formal methods Year 4 Addition and Subtraction up to 4 digits using formal methods (Solve simple measure and money problems involving decimals to 2 dp) Year 5 Addition & Subtraction more than 4 digits using formal methods (Solve problems involving number up to 3 dp) (They mentally add & subtract tenths, and one-digit whole numbers and tenths) (They practise adding & subtracting decimals, including a mix of whole numbers and decimals, decimals with different numbers of decimal places, and complements of 1 (for example, 0. 83 + 0. 17 = 1)). All years groups also refer to "estimation", "inverse operations" to check, "problem solving”
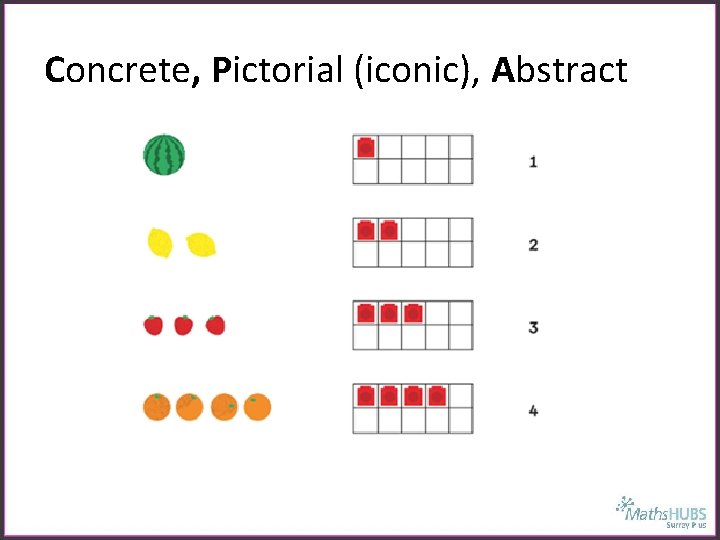
Concrete, Pictorial (iconic), Abstract
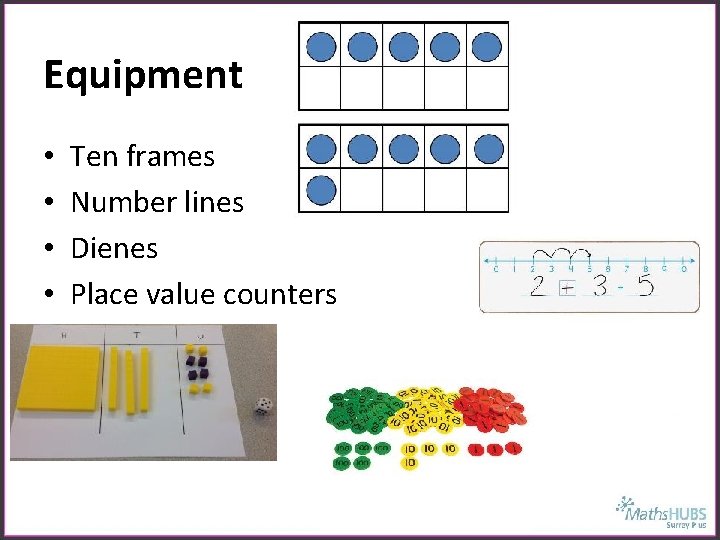
Equipment • • Ten frames Number lines Dienes Place value counters

+ 25 = 15 + 24 14 + = 15 + 24 16 + = 15 + 24

Choosing methods 346 + 295 346 + 300 – 5 Do you ever ask children to reflect on their method?

Number stories

Bar Models 6 15 9
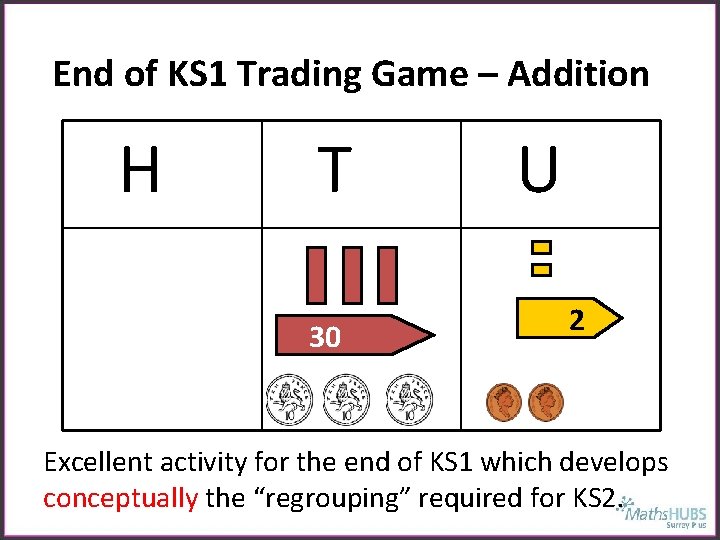
End of KS 1 Trading Game – Addition H T 30 U 2 Excellent activity for the end of KS 1 which develops conceptually the “regrouping” required for KS 2.

Three-Digit Column Addition – Stage 1 Students will still require concrete resources, even if they say they don’t! This is likely to be Dienes (or equivalent) to model two digit addition. No re-grouping to take place. Students record concrete and abstract calculations together. T U 2 3 + 4 1

Three-Digit Column Addition – Stage 2 Students will still require concrete resources, even if they say they don’t! This is likely to be Dienes (or equivalent) to model two digit addition. Students record concrete and abstract calculations together. T U 2 5 + 4 7
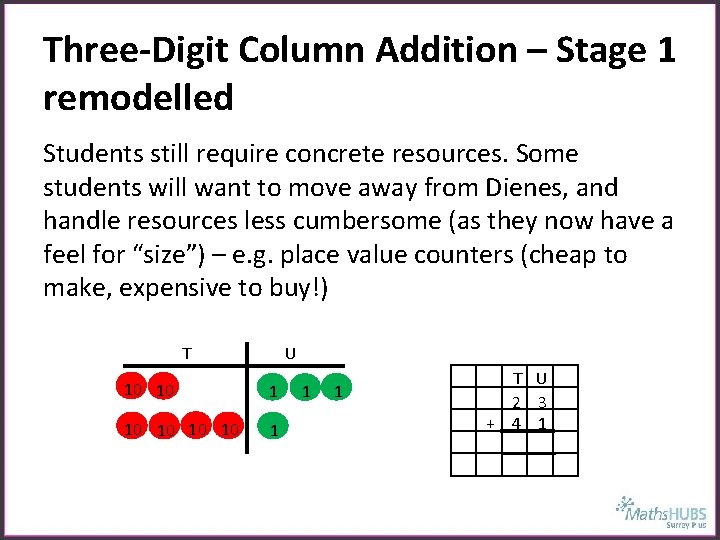
Three-Digit Column Addition – Stage 1 remodelled Students still require concrete resources. Some students will want to move away from Dienes, and handle resources less cumbersome (as they now have a feel for “size”) – e. g. place value counters (cheap to make, expensive to buy!) T U 10 10 1 1 1 T U 2 3 + 4 1
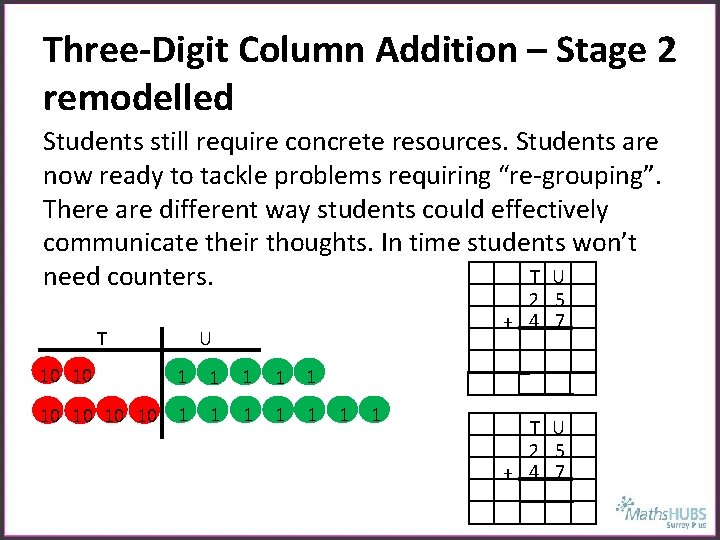
Three-Digit Column Addition – Stage 2 remodelled Students still require concrete resources. Students are now ready to tackle problems requiring “re-grouping”. There are different way students could effectively communicate their thoughts. In time students won’t T U need counters. T 2 5 + 4 7 U 10 10 1 1 1 1 T U 2 5 + 4 7
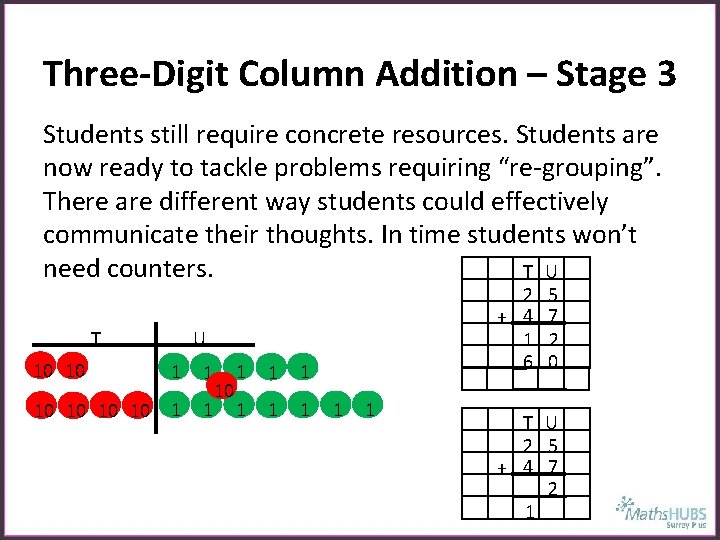
Three-Digit Column Addition – Stage 3 Students still require concrete resources. Students are now ready to tackle problems requiring “re-grouping”. There are different way students could effectively communicate their thoughts. In time students won’t need counters. T U T 2 + 4 1 6 U 10 10 1 1 10 1 1 1 1 5 7 2 0 T U 2 5 + 4 7 2 1
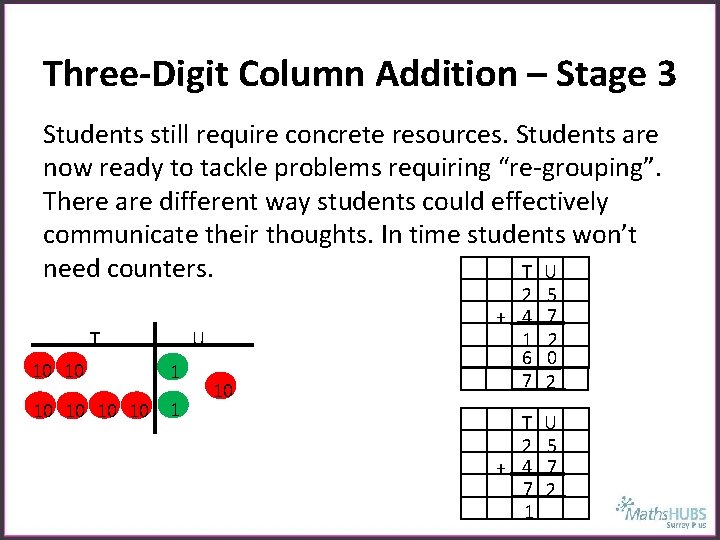
Three-Digit Column Addition – Stage 3 Students still require concrete resources. Students are now ready to tackle problems requiring “re-grouping”. There are different way students could effectively communicate their thoughts. In time students won’t need counters. T U 10 10 1 10 2 + 4 1 6 7 5 7 2 0 2 T 2 + 4 7 1 U 5 7 2
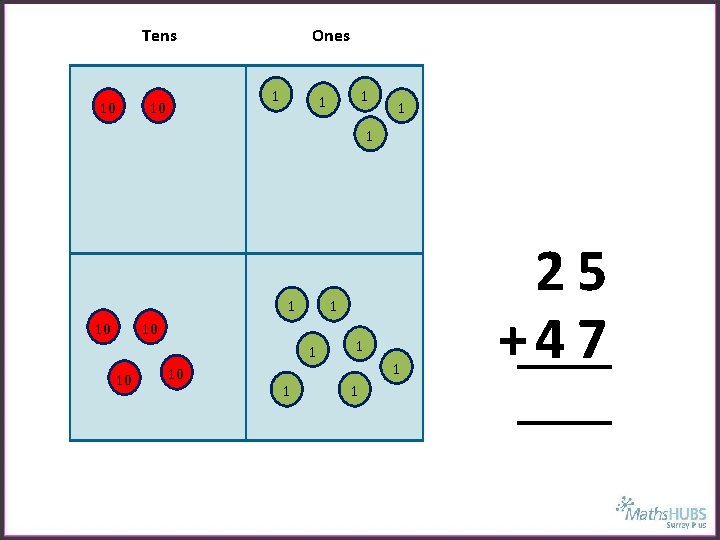
Tens 10 Ones 1 10 1 10 10 1 1 25 +4 7

Practice time – what do you notice in the progression of the questions? 345 + 123 345 + 126 345 + 183 345 + 186

Challenge by going deeper – not just bigger numbers! 1) Find the perimeter of this shape: 12 4 26 8 359 2) Show this pattern goes up by the same amount each time. Then find the next number in the pattern: 325, 462, 599, …

Identifying common misconceptions: Mark the following questions. If they are right give a tick, if they are wrong, explain why you think the mistake has been made: + 2 9 5 3 4 6 9 1 1 4 1 + 295 34 6 32 96 1 Reflection: is column addition the most efficient way to tackle this question?
Subtraction

Subtraction problems I had 9 apples but my rabbit ate 3 of them. How many did I have left? (Take away model) I had 9 apples. My friend Harry had 3 apples. How many more apples did I have? (Difference model)
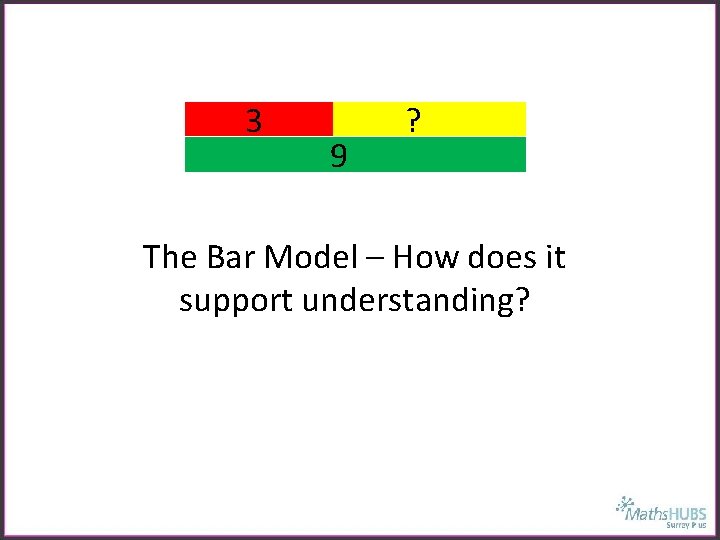
3 9 ? The Bar Model – How does it support understanding?
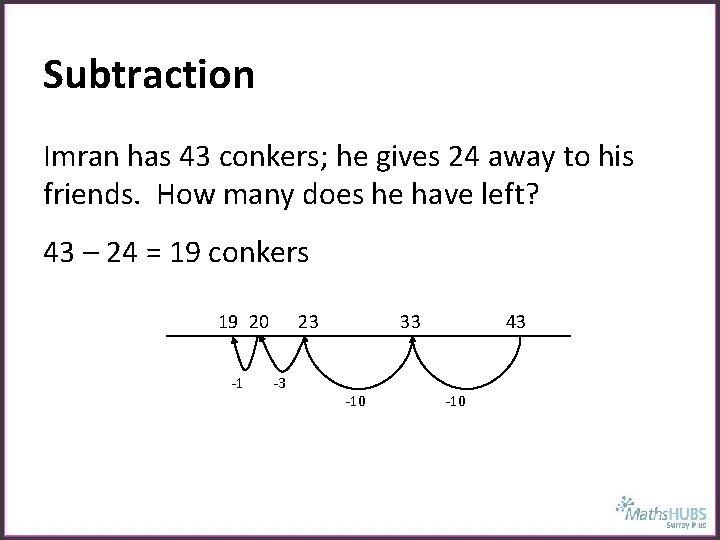
Subtraction Imran has 43 conkers; he gives 24 away to his friends. How many does he have left? 43 – 24 = 19 conkers 19 20 -1 23 -3 33 -10 43 -10
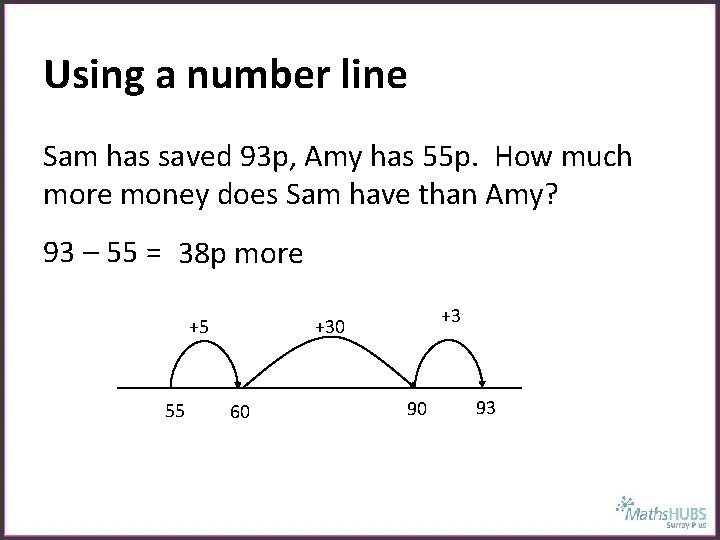
Using a number line Sam has saved 93 p, Amy has 55 p. How much more money does Sam have than Amy? 93 – 55 = 38 p more 55 +3 +30 +5 60 90 93

Robber maths 43 – 13 The number you need to subtract is small enough to “pick it up and take it away”

Mind the gap 74 - 69 The gap between the two numbers is smaller so it is more efficient to find the difference (probably by counting on)

Robber maths or mind the gap? 101 – 99 63 – 21 84 – 78 1006 – 999 86 – 14
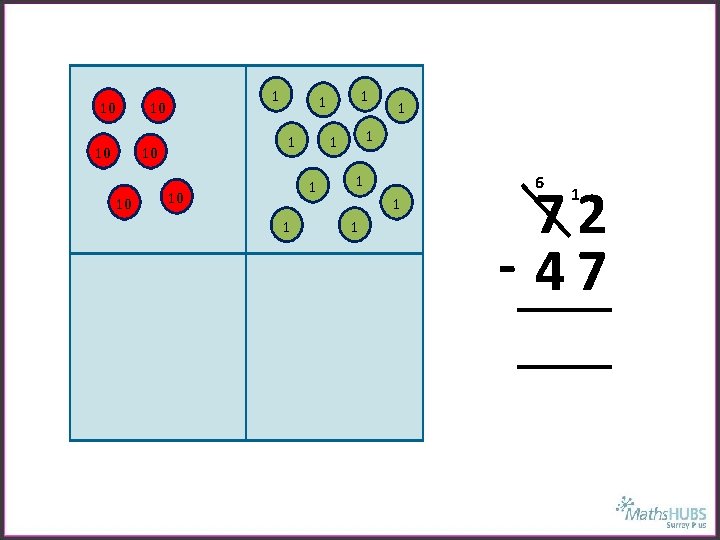
10 10 1 10 10 1 1 1 6 1 1 1 72 - 47 1
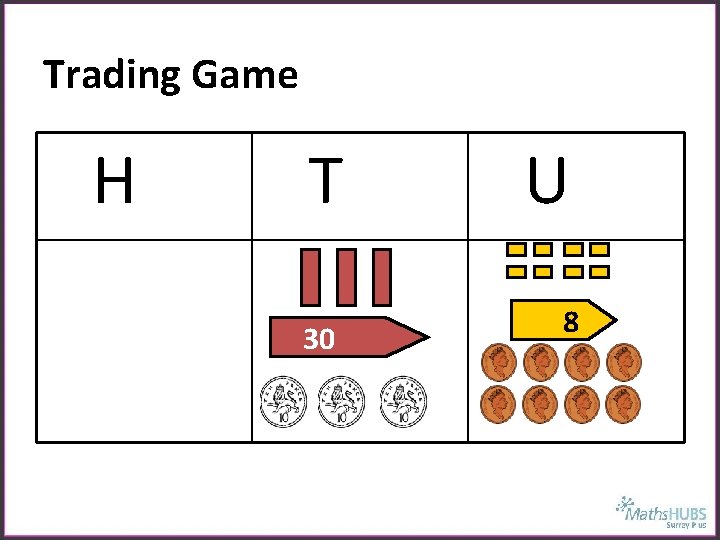
Trading Game H T 30 U 8

Practice time - what do you notice in the progression of the questions? 345 - 123 345 - 126 345 - 183 345 - 186

Decomposition vs equal addition • The operation of subtraction can often be simplified by adding a quantity to the number being subtracted (the subtrahend), making it a multiple of ten. The quantity added to the subtrahend must also be added to the minuend. Example: Simplify 87 - 56. Adding 4 to the minuend and subtrahend makes the subtraction easier to complete. 87 - 56 = (87 + 4) - (56 + 4) = 91 - 60 = 31
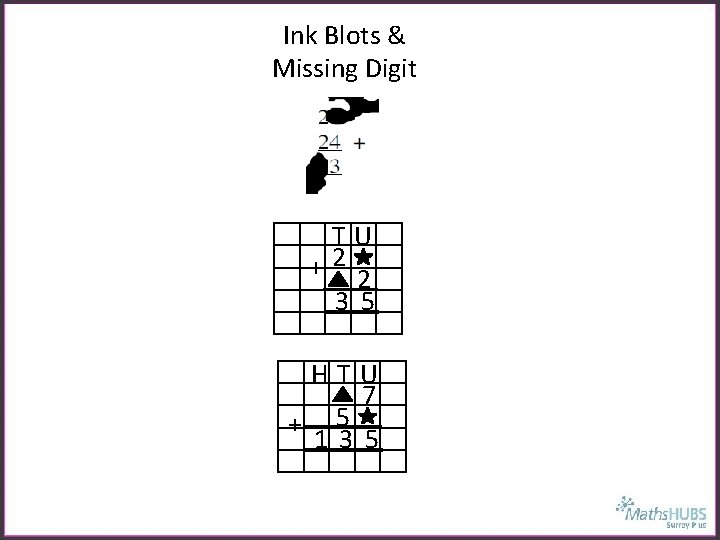
Ink Blots & Missing Digit TU +2 2 3 5 HTU 7 + 5 1 3 5
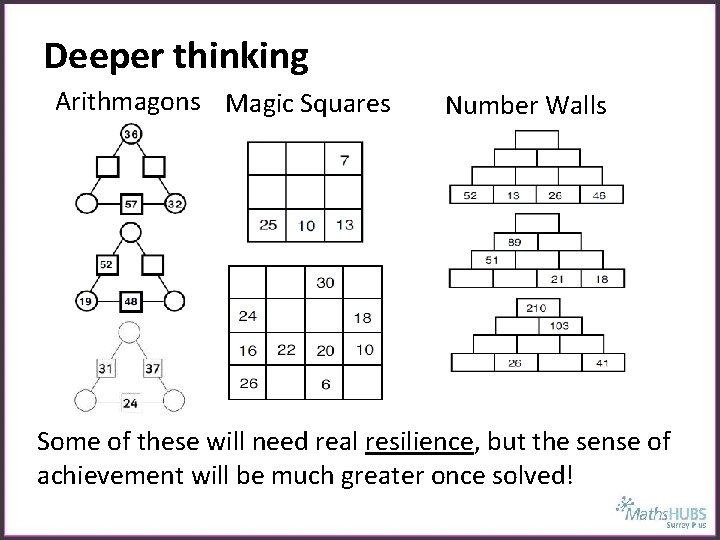
Deeper thinking Arithmagons Magic Squares Number Walls Some of these will need real resilience, but the sense of achievement will be much greater once solved!

Where now? Reflect on the addition and subtraction journey. What are the most important messages you are going to take away? * * * Where next? Progress in multiplication.
- Slides: 37