T 4 4 Linear Systems Matrices IB Math

T 4. 4 – Linear Systems & Matrices IB Math SL - Santowski

Fast Five n (1) If A and B are both n by n matrices, is AB = BA? n (2) Solve the equation 8 x = 16 without using division n (3) Multiply the matrices

(A) Linear Systems n At this point in math, you have 2 major ways to solve linear systems: n n (a) Algebraic (Elimination or Substitution) (b) Graphic (look for intersection point) n So solve the system defined by: n L 1: 2 x + y = 6 L 2: 3 x+4 y = -1 n
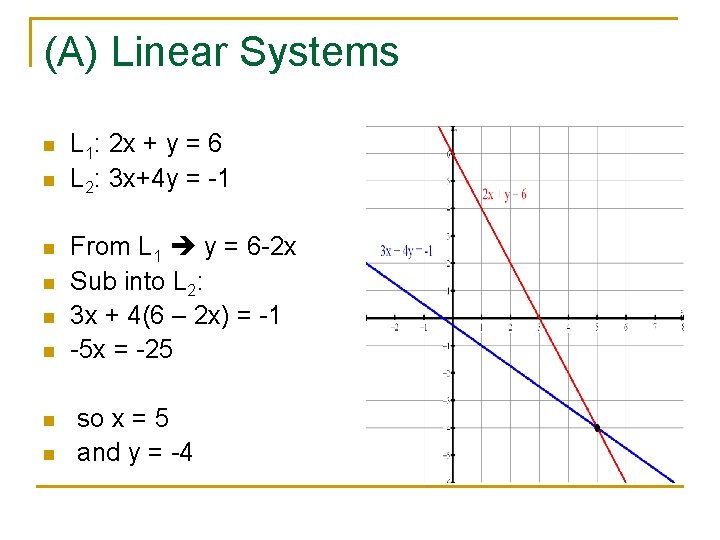
(A) Linear Systems n n n n L 1: 2 x + y = 6 L 2: 3 x+4 y = -1 From L 1 y = 6 -2 x Sub into L 2: 3 x + 4(6 – 2 x) = -1 -5 x = -25 so x = 5 and y = -4

(A) Linear Systems & Matrices n So let’s combine linear systems & matrices n So HOW do you write the system below as a matrix? ? ? (see fast five) n L 1: 2 x + y = 6 L 2: 3 x+4 y = -1 n

(A) Linear Systems & Matrices n So the system n L 1: 2 x + y = 6 L 2: 3 x+4 y = -1 n Now becomes a matrix multiplication as …. n and

(A) Linear Systems & Matrices n So the system n L 1: 2 x + y = 6 L 2: 3 x+4 y = -1 n Now becomes a matrix multiplication as …. n and

(A) Linear Systems & Matrices n So how do we “multiply” matrices for the viewpoint of isolating an unknown (or isolating the variables matrix? ) n Ax = B

(A) Linear Systems & Matrices n So how do we multiply matrices for the viewpoint of isolating an unknown (or isolating the variables matrix? ) USE THE INVERSE!!! n But HOW? ? ? recall that the order in which you multiply matrices IS IMPORTANT

(B) Matrix Multiplication (A Review) n Define the following matrices on your TI-83/4 n so the system you are investigating is: n So carry out the following multiplications Which statements are true?

(B) Matrix Multiplication (A Review) n So carry out the following multiplications Which statements are true? n So, since statements (a) and (d) are true, how does this relate to solving equations using matrices? ?

(B) Matrix Multiplication (A Review) n So, since statements (a) and (d) are true, how does this relate to solving equations using matrices? ? n Recall that the product of a matrix and its inverse is I n So what we have effectively accomplished is ISOLATING the variable matrix WITHOUT using division!!

(C) Matrices and Linear Equations n So let’s consolidate everything: n So use matrices to solve the system defined by: n L 1: 2 x + y = 6 L 2: 3 x+4 y = -1 n

(C) Matrices and Linear Equations

(D) Examples – Matrices & Linear Systems n (1) Solve the system: –x+5 y = 4 and 2 x + 5 y = -2. Interpret your solution. n (2) Solve the system x + 2 y – z = 6 and 3 x + 5 y – z = 2 and -2 x – y – 2 z = 4. Interpret your solution.

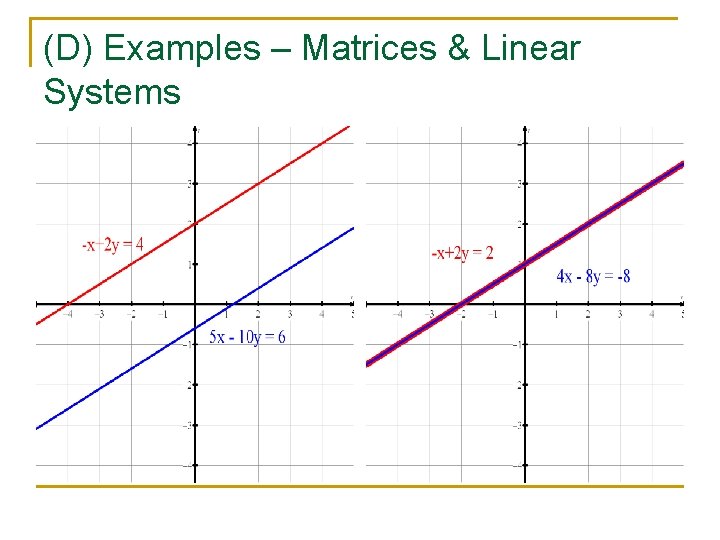
(D) Examples – Matrices & Linear Systems n (1) Solve the system: -x + 2 y = 4 and 5 x – 10 y = 6. Interpret your solution. n (2) Solve the system –x + 2 y = 2 and 4 x – 8 y = -8. Interpret your solution.

(D) Examples – Matrices & Linear Systems n (1) Solve the system: L 1: -x + 2 y = 4 (y = ½x + 2 ) and L 2: 5 x – 10 y = 6 (y = ½x – 0. 6) Interpret your solution. n (2) Solve the system L 1: –x + 2 y = 2 (y = -½x +1) and L 2: 4 x – 8 y = -8 (y = -½x +1). Interpret your solution. n So if det[A] = 0, then ……? ? ? ?
(D) Examples – Matrices & Linear Systems

(D) Examples – Matrices & Linear Systems n Consider the system 2 x + ky = 8 and 4 x – y = 11. n (a) Calculate det[A] n (b) for what value(s) of k does the system have a unique solution? Find the unique solution. n (c) for what value(s) of k does the system not have a unique value. How many solutions does it have in this case?

(D) Examples – Matrices & Linear Systems n (a) Show that if AX = B, then X = A-1 B whereas if XA = B, then X = BA-1. n (b) Solve for X if n n (c) Solve for X if

(D) Examples – Matrices & Linear Systems n Given that n Solve for X if AXB = C. n

(D) Examples – Matrices & Linear Systems

(D) Examples – Matrices & Linear Systems

(D) Examples n (1) Find all matrices X that satisfy the equation n (2) Find all matrices X that satisfy the equation n (3) Find all real numbers a and b if a. X 2 + b. X = 2 I and

(D) Examples n (4) Find the matrix A and express a, b and c in terms of p if the system of equations n (5) for what values of k is the matrix A singular if

(D) Examples n (6) For what values of k is A singular if n (7) For what value(s) of m will the given system of equations have: n (a) a unique solution (b) no solution? (c) an infinite number of solutions n n

Homework n n Matrices & Systems: Ex 14 H #2 ad, 8 acf; Ex 14 I #1 a, 3 ab, 4 b, 7; Ex 14 K #2 a; Ex 14 L #5 a, 8; n 3 x 3 matrices Ex 14 H #5; Ex 14 I #5 ac, 6, 8 b; Ex 14 J#1 agh, 3, 6 a n IB Packet #1, 2, 4, 5, 7 n n n
- Slides: 27