Systmy pro podporu managementu 2 3 Vcekriteriln rozhodovn

Systémy pro podporu managementu 2 3 - Vícekriteriální rozhodování, Teorie her a rozhodovací modely

Obsah přednášky l l Vícekriteriální rozhodování Teorie her

Vícekriteriální rozhodování 1 l l Nejednodušší situace – rozhodování podle jednoho kritéria Složitější případ – více kriterií l l l Podle důležitosti Paralelní respektování kriterií Pomocí užitkových funkcí převést na rozhodování při jednom kritériu

Vícekriteriální rozhodování 2 l Vícekriteriální optimalizační model l l Nekonečně přípustných řešení Alespoň dvě účelové funkce -> vícekriteriální lineární optimalizační model Model vícekriteriální analýzy variant l l l Konečný počet přípustných řešení Každá varianta je hodnocena podle několika kriterií Komponenty modelu: varianty, kritéria, kriteriální matice, váhy kritérií

Vícekriteriální rozhodování 3 l Ideální a bazální varianta l Ideální řešení (varianta) je hypotetické nebo reálné řešení, reprezentované ve všech kritériích současně nejlepšími možnými hodnotami. l l varianta H s ohodnocením (h 1, . . . , hk) Bazální řešení (varianta) je hypotetické nebo reálné řešení, reprezentované nejhorším ohodnocením podle všech kritérií. l varianta D s ohodnocením (d 1, . . . , dk).

Vícekriteriální rozhodování 4 l Dominance řešení l l l V této definici předpokládáme všechna kritéria maximalizační. Varianta ai dominuje variantu aj , jestliže pro její ohodnocení platí (yi 1, yi 2 , …, yik) ≥ (yj 1, yj 2, …, yjk) a existuje alespoň jedno kritérium fl , že yil > yjl. Řešení je nedominované (efektivní) řešení problému, pokud neexistuje žádné jiné řešení, které by jej dominovalo.

Vícekriteriální rozhodování 5 l Kompromisní řešení l Kompromisní varianta (řešení) má od ideální varianty (řešení) nejmenší vzdálenost podle vhodné metriky (měřenou vhodným způsobem). l Kompromisem může být i zanedbání některých kritérií.

Vícekriteriální rozhodování 6 l Cíl řešení modelů l l l Nalezení jediné kompromisní varianty, kompromisního řešení (Nalezení určitého počtu kompromisních variant) Rozdělení řešení na efektivní a neefektivní Uspořádání všech řešení od nejlepšího k nejhoršímu

Vícekriteriální rozhodování 7 l Metody kvantifikace informace 1 l Metoda pořadí l l Bodovací metoda l l nejlepší varianta, nejdůležitější kritérium bude první v pořadí nejlepší varianta, nejdůležitější kritérium dostane nejvíce bodů Párové porovnávání l porovnává se důležitost kritérií či ohodnocení variant podle jednotlivých kritérií

Vícekriteriální rozhodování 8 l Metody kvantifikace informace 2 l Saatyho metoda l Metoda kvantitativního párového porovnání l Stupnice: § § § l l 1…rovnocenné 3…slabá preference 5…silná preference 7…velmi silná preference 9…absolutní preference Saatyho matice – čtvercová, reciproční Váhy – normalizovaný geometrický průměr řádků Saatyho matice

Vícekriteriální rozhodování 9 l Metody l l Metody nevyžadující informaci o preferenci kritérií l Bodovací metoda a metoda pořadí Metody vyžadující ordinální informace l Lexikografická metoda Metody vyžadující kardinální informaci l Metody založené na výpočtu hodnot funkce užitku l Metoda váženého součtu l Metoda AHP – Analytický hierarchický proces Metody založené na minimalizaci vzdálenosti od ideální varianty l Metoda TOPSIS

Teorie her l l l Co je teorie her? Základní pojmy Hry s nulovým součtem Hry s nenulovým součtem Herní strategie

Co je teorie her? l l l Teorie sociálních situací (psychologie) Kooperativní a nekooperativní hry Racionální volba l l Matematická teorie rozhodování racionálních hráčů, kteří jsou na sobě závislí Vaše nejlepší rozhodnutí záleží na tom, co dělají ostatní, a co oni dělají, může být závislé na tom, co si oni myslí, že vy učiníte… Analýza mezinárodních konfliktů (T. Schelling) i spolupráce (R. Axelrod) Nezaručuje výhru, ale pomáhá pochopit

Základní pojmy l l l Hráči – kdo se účastní hry Strategie – jaké jsou možnosti Výplaty – jaké jsou odměny hráčů Informace – co se ví Racionalita – jak hráči myslí

Hra s nulovým součtem l l l Pro jednotlivé kombinace strategií je součet výplat roven 0 Dokonale antagonistické hry – zisk jednoho hráče = ztráta druhého Zápis v maticovém tvaru – nejjednodušší situace = dva hráči, dvě strategie

Příklad hry s nulovým součtem Irák Bez podpory USA Vojenský útok Diplomatický tlak S podporou (10, -10) (-5, 5) (0, 0) (-2, 2) (první číslo v závorce – výplata prvního hráče = USA, druhé číslo v závorce – výplata druhého hráče = Irák) Pro prvního hráče je nejvýhodnější, aby oba hráli první strategii, pro druhého hráče je to naopak. Rovnovážným bodem je (-2, 2) – pokud se v něm hráči ocitnou, ani jeden nemá zájem měnit strategii – Nashova rovnováha

Hra s nenulovým součtem l Možnost komunikace a dohody hráčů l l Kooperativní hry – hráči mohou komunikovat a uzavírat dohody ohledně strategií Nekooperativní hry- dohody možné nejsou a komunikace může a nemusí být možná

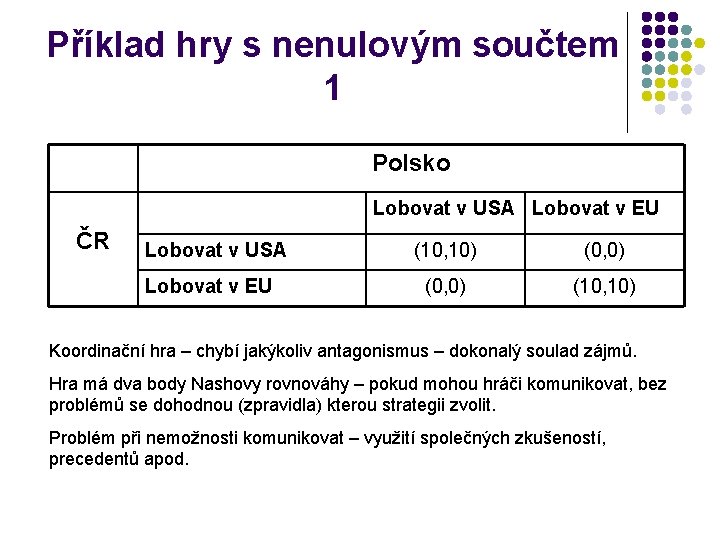
Příklad hry s nenulovým součtem 1 Polsko Lobovat v USA Lobovat v EU ČR Lobovat v USA Lobovat v EU (10, 10) (0, 0) (10, 10) Koordinační hra – chybí jakýkoliv antagonismus – dokonalý soulad zájmů. Hra má dva body Nashovy rovnováhy – pokud mohou hráči komunikovat, bez problémů se dohodnou (zpravidla) kterou strategii zvolit. Problém při nemožnosti komunikovat – využití společných zkušeností, precedentů apod.

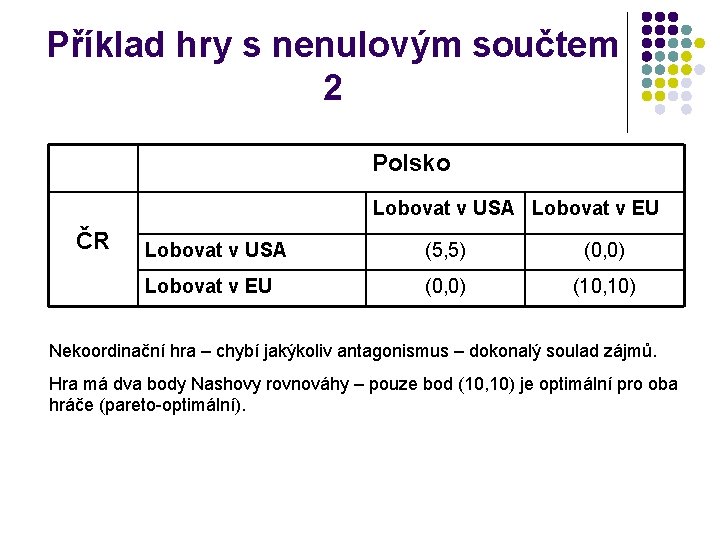
Příklad hry s nenulovým součtem 2 Polsko Lobovat v USA Lobovat v EU ČR Lobovat v USA (5, 5) (0, 0) Lobovat v EU (0, 0) (10, 10) Nekoordinační hra – chybí jakýkoliv antagonismus – dokonalý soulad zájmů. Hra má dva body Nashovy rovnováhy – pouze bod (10, 10) je optimální pro oba hráče (pareto-optimální).

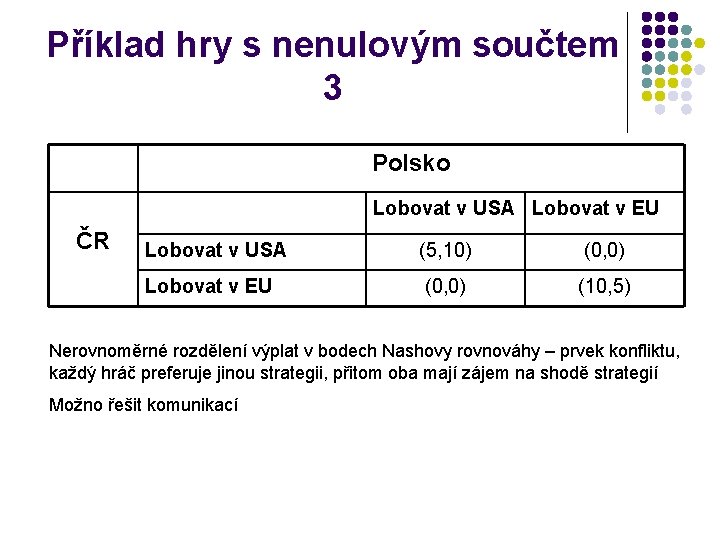
Příklad hry s nenulovým součtem 3 Polsko Lobovat v USA Lobovat v EU ČR Lobovat v USA (5, 10) (0, 0) Lobovat v EU (0, 0) (10, 5) Nerovnoměrné rozdělení výplat v bodech Nashovy rovnováhy – prvek konfliktu, každý hráč preferuje jinou strategii, přitom oba mají zájem na shodě strategií Možno řešit komunikací

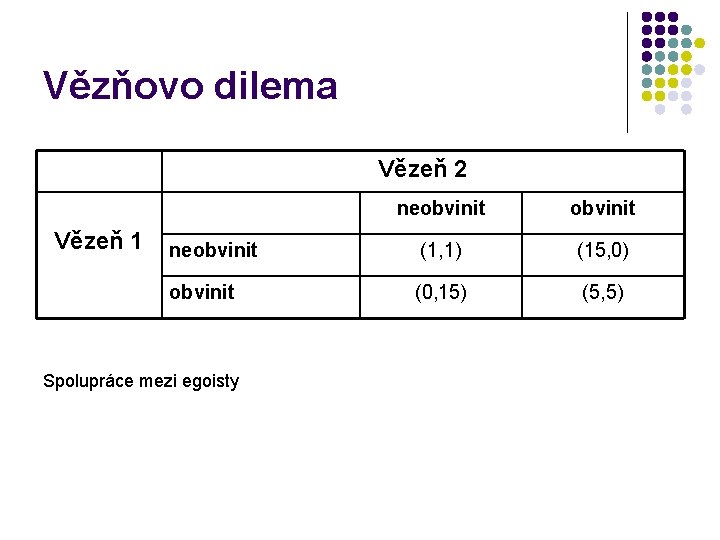
Vězňovo dilema Vězeň 2 Vězeň 1 neobvinit (1, 1) (15, 0) obvinit (0, 15) (5, 5) Spolupráce mezi egoisty

Herní strategie l Při jednom opakování: l l l obvinit, neobvinit (vězeňské dilema) Poslat, neposlat/ponechat, vrátit (investiční hra) Při více opakování: l l „Tit for tat“ (oko za oko, zub za zub – hrej „obvinit“, když druhý hráč zahrál “obvinit“, hrej „neobvinit“, když druhý hráč zahrál „neobvinit“) „Grim trigger“ (hrej „poslat“ dokud příjemce hraje „vrátit“; jakmile příjemce zahraje „ponechat“, nikdy nehraj „poslat“)

Odkazy a experimenty l Vězňovo dilema a další hry: l http: //www. gametheory. net/applets/

Naučil jsem se prokazovat službu druhému, aniž bych mu ve skutečnosti poskytl jakoukoli laskavost. Předvídám totiž, že mi dotyčný se stejným očekáváním službu oplatí, aby tak zachoval vzájemné poskytování laskavostí se mnou i s druhými. A když jsem mu tedy posloužil a on si užívá výhod vyplývajících z mého činu, pociťuje, že je řada opět na něm, neboť předvídá důsledky, jež by mělo jeho odmítnutí. David Hume