Systems with Matrices Skill 20 Objectives Write matrices

Systems with Matrices Skill 20

Objectives • • Write matrices and identify their dimensions Use elementary row operations on matrices Solve systems using Gaussian elimination and matrices Solve systems using Gauss-Jordan elimination

Cramer’s Rule • So far, you have studied three methods for solving a system of linear equations: substitution, elimination with equations, and elimination with matrices. You will now study one more method, Cramer’s Rule, named after Gabriel Cramer (1704– 1752). • This rule uses determinants to write the solution of a system of linear equations.

Example; Matrix Multiplication

Example; Solve Using Cramer’s Rule

Example; Solve Using Cramer’s Rule
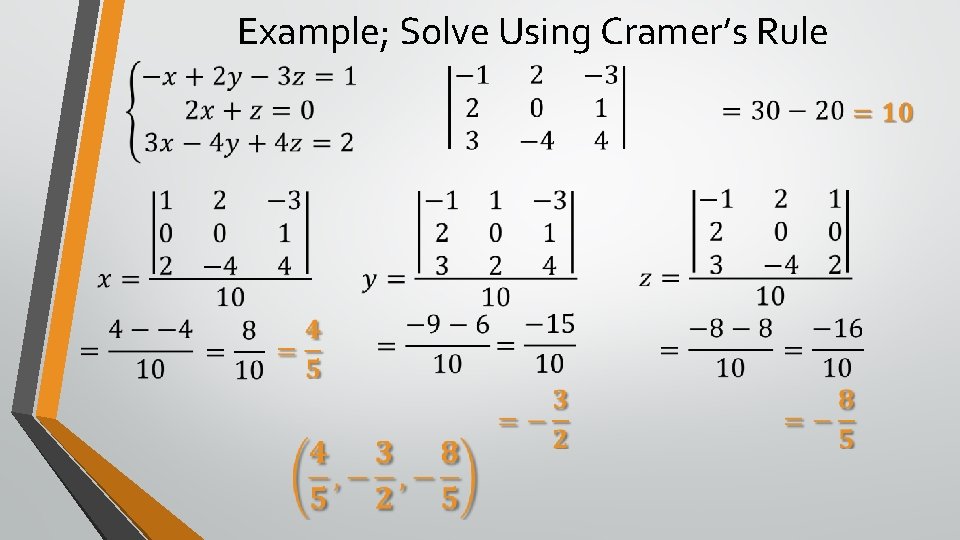
Example; Solve Using Cramer’s Rule

Example; Solve Using Cramer’s Rule

Systems with Inverse Matrices
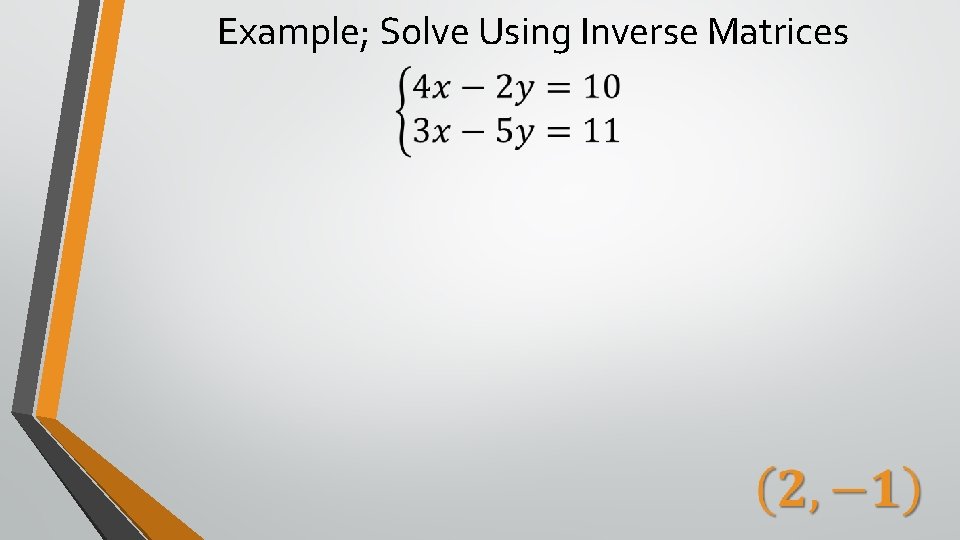
Example; Solve Using Inverse Matrices
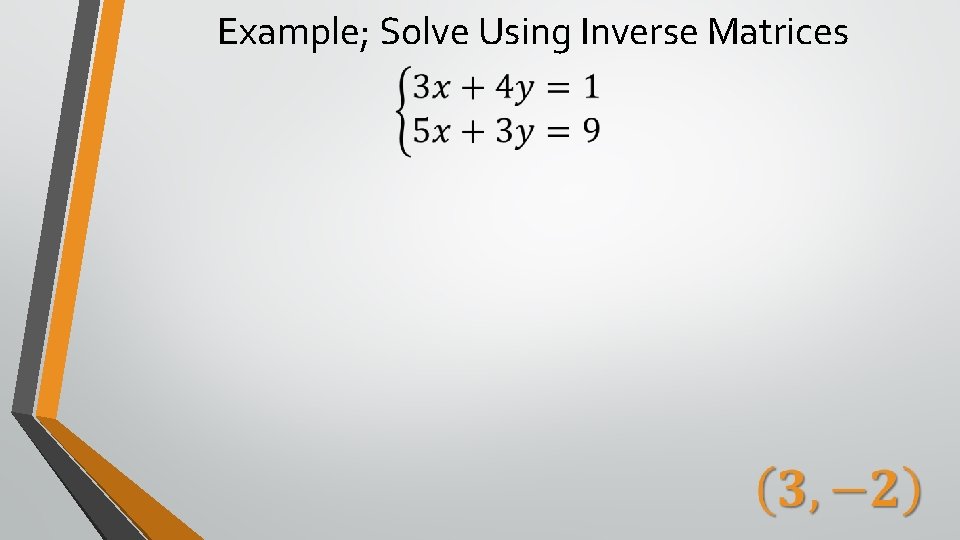
Example; Solve Using Inverse Matrices

Definitions A matrix derived from a system of linear equations (each written in standard form with the constant term on the right) is the augmented matrix of the system. Moreover, the matrix derived from the coefficients of the system (but not including the constant terms) is the coefficient matrix of the system. The matrix derived from the constant terms of the system is the constant matrix of the system.

Example; Understanding Augmented matrices System: Augmented Matrix:
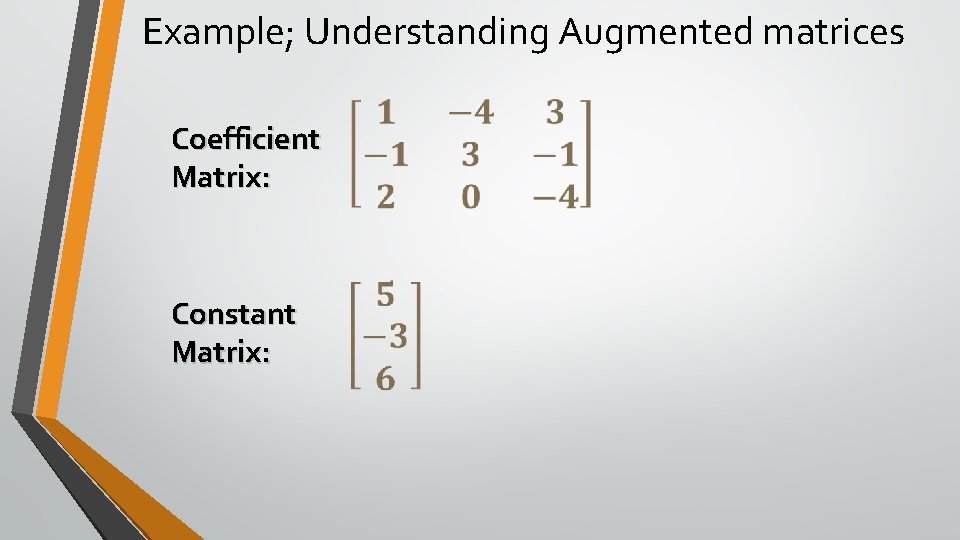
Example; Understanding Augmented matrices Coefficient Matrix: Constant Matrix:

Elementary Row Operations 1) Interchange two rows 2) Multiply one of the rows by a nonzero constant 3) Add a multiple of one row to another row

Example; Using Gaussian Elimination and matrices Augmented Matrix

Example; Using back-substitution

Example; Using Gaussian Elimination and matrices Augmented Matrix

Example; Using Gaussian Elimination and matrices

Example; Using back-substitution

Gauss-Jordan Elimination With Gaussian elimination, elementary row operations are applied to a matrix to obtain a (row-equivalent) row-echelon form of the matrix. A second method of elimination, called Gauss-Jordan elimination after Carl Friedrich Gauss (1777– 1855) and Wilhelm Jordan (1842– 1899), continues the reduction process until a reduced row-echelon form is obtained.

Example; Using Gauss-Jordan Elimination Row-Echelon Form:

Example; Using Gauss-Jordan Elimination Augmented Matrix:

Example; Using Gauss-Jordan Elimination Augmented Matrix:

Example; Using Gaussian Elimination and matrices Augmented Matrix

Example; Using Gaussian Elimination and matrices

20: Matrices and Solving Systems • Summarize your notes • Questions? • Homework • Worksheet • Quiz
- Slides: 27