Systems of ODEs Ordinary Differential Equations June 8

Contents § § § 13. 1 Higher Order ODEs 13. 2 Systems of Two

13. 1 Higher Order ODEs § A higher order ODE can be converted into

Ex. 13. 1 § Nonlinear pendulum Simple pendulum Choosing g/L=1 and c/(m. L)=0. 3,

13. 1 Higher Order ODEs (Cont’d) § A higher order ODE may be converted

13. 2 Systems of two first-order ODEs § 13. 2. 1 Euler’s method for

Ex. 13. 2 § Nonlinear pendulum using Euler’s Method Ø To apply the basic

13. 2 Systems of two first-order ODEs (Cont’d) § Matlab code Computer Vision &

Ex. 13. 3 § Series dilution problem using Euler’s method u=c 1, v=c 2

13. 2. 2 Midpoint method for solving two ODE-IVPs § The idea is same

13. 2. 2 Midpoint method for solving two ODE-IVPs Using k 1 and k

13. 2. 2 Midpoint method for solving two ODE-IVPs § Matlab code Computer Vision

Ex. 13. 4 § Nonlinear pendulum using Runge-Kutta method The computed solution for n=50,

Ex. 13. 5 § Series dilution using Runge-Kutta technique The exact solutions, viz. ,

13. 3 Systems of First-order ODE-IVPs § Application: chemical reactions, predator-prey models, and many

13. 3. 1 Euler’s Method for Solving Systems of ODEs § The basic Euler

Ex 13. 8 § Solving a Higher Order System using Euler’s Method with initial

13. 3. 2 Runge-Kutta Methods for Solving Systems of ODEs § Second order Runge-Kutta

System Using a Second-Order Runge-Kutta Method (Midpoint Method) § Matlab code function [ x,

Ex 13. 9 § Solving a Higher Order System using a Runge-Kutta Method Ø

Ex 13. 10 § Solving a Higher Order System using a Runge-Kutta Method Ø

Ex 13. 10 (cont’d) The approximate solution at x = 1. 5: finding k

Ex 13. 10 (cont’d) The approximate solution at x = 2. 0: Ø Matlab

Ex 13. 10 (cont’d) § n = 10 Ø Matlab code • [x, u]

Fourth-Order Runge-Kutta Method § Matlab code %function f(x, u); a = tspan(1); b =

Ex 13. 11 § Solving a Circular Chemical Reaction Using a Runge-Kutta Method r

13. 3. 3 Multistep Methods for System § The basic two-step Adams-Bashforth method y

13. 3. 3 Multistep Methods for System § The basic two-step Adams-Bashforth method (cont’d)

Adams-Bashforth-Moulton § § Predictor-corrector methods Matlab code function [x, u] = ABM 3_sys(f, tspan,

Ex 13. 12 Mass-and-Spring System § The vertical displacements of two masses m 1

Ex 13. 12 Mass-and-Spring System § Matlab code a = 0; b = 5;

Ex 13. 13 Motion of a Baseball § Air resistance is one of the

Ex 13. 13 Motion of a Baseball 1. Air Resistance Proportional to Velocity in

Stiff ODE and ILL-Conditioned Problem § Ill condition Ø ODE for which any error

Stiff ODE and ILL-Conditioned Problem § ill condition Ø Consider the ODE Ø The

Stiff ODE and ILL-Conditioned Problem § ill condition Ø Consider the ODE u’ =

Using Matlab’s Functions § The Matlab Functions Ø ODE 23 • The Matlab functions

Using Matlab’s Functions § The Matlab Functions Ø ODE 23 • To solve the

Using Matlab’s Functions § The Matlab Functions Ø ODE 23 • robot 2_1 Initialize

Using Matlab’s Functions § The Matlab Functions Ø ODE 23 • Result • Figure

Slides: 41

Download presentation

Systems of ODEs (Ordinary Differential Equations) June 8, 2005 Sung-Min Kim, Ho-Kuen Shin, A-Yon Park Computer Vision & Pattern Recognition Lab. Dept. of Computer Science & Engineering, Korea Univ.

Contents § § § 13. 1 Higher Order ODEs 13. 2 Systems of Two First-Order ODEs 13. 3 Systems of First-Order ODE-IVPs 13. 4 Stiff ODE and Ill-Conditioned Problems 13. 5 Using MATLAB’s Functions Computer Vision & Pattern Recognition Lab.

13. 1 Higher Order ODEs § A higher order ODE can be converted into a system of first-order ODEs Ø A second-order ODE of the form can be converted to system of two first-order ODEs by a simple change of variables : the differential equations relating these variables are the initial conditions for the original ODE, become the initial conditions for the system, i. e. , Computer Vision & Pattern Recognition Lab.

Ex. 13. 1 § Nonlinear pendulum Simple pendulum Choosing g/L=1 and c/(m. L)=0. 3, a=π/2 and b=0. Second-order ODE-IVP Computer Vision & Pattern Recognition Lab.

13. 1 Higher Order ODEs (Cont’d) § A higher order ODE may be converted to a system of first order ODEs by a similar change of variables Ø The nth-order ODE a system of first-order ODEs by the following change of variables; the differential equations relating these variables are with initial conditions Computer Vision & Pattern Recognition Lab.

13. 2 Systems of two first-order ODEs § 13. 2. 1 Euler’s method for solving two ODE-IVPs Ø To apply the basic Euler’s method to the system of ODEs update the function u using f(x, u, v) and update v using g(x, u, v) Computer Vision & Pattern Recognition Lab.

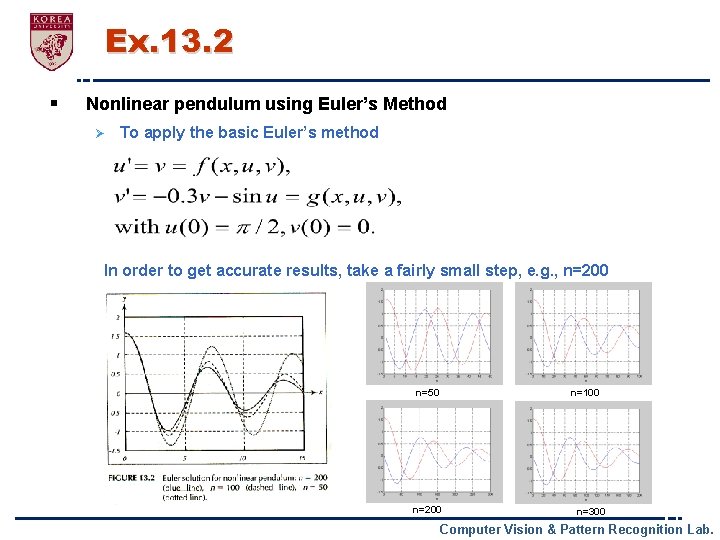
Ex. 13. 2 § Nonlinear pendulum using Euler’s Method Ø To apply the basic Euler’s method In order to get accurate results, take a fairly small step, e. g. , n=200 n=50 n=100 n=200 n=300 Computer Vision & Pattern Recognition Lab.

13. 2 Systems of two first-order ODEs (Cont’d) § Matlab code Computer Vision & Pattern Recognition Lab.

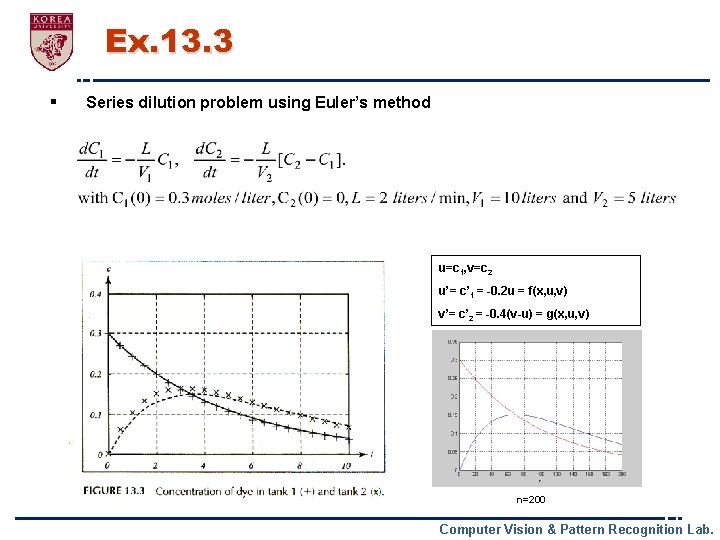
Ex. 13. 3 § Series dilution problem using Euler’s method u=c 1, v=c 2 u’= c’ 1 = -0. 2 u = f(x, u, v) v’= c’ 2 = -0. 4(v-u) = g(x, u, v) n=200 Computer Vision & Pattern Recognition Lab.

13. 2. 2 Midpoint method for solving two ODE-IVPs § The idea is same as for Euler’s method Ø Update each unknown function u and v, using the basic Runge-Kutta formulas rewrite the basic second-order Runge-Kutta formulas, Computer Vision & Pattern Recognition Lab.

13. 2. 2 Midpoint method for solving two ODE-IVPs Using k 1 and k 2 to represent the update quantities for the unknown u Ø Calling the corresponding quantities for function v, m 1 and m 2 Ø Update function f by the appropriate multiple of k 1 or k 2 and function g by the corresponding amount of m 1 or m 2 Ø • This means that k 1 and m 1 must be computed before k 2 and m 2 can be found thus, Computer Vision & Pattern Recognition Lab.

13. 2. 2 Midpoint method for solving two ODE-IVPs § Matlab code Computer Vision & Pattern Recognition Lab.

Ex. 13. 4 § Nonlinear pendulum using Runge-Kutta method The computed solution for n=50, n=100, and n=200 are indistinguishable n=50 n=200 n=100 n=300 Computer Vision & Pattern Recognition Lab.

Ex. 13. 5 § Series dilution using Runge-Kutta technique The exact solutions, viz. , Computer Vision & Pattern Recognition Lab.

13. 3 Systems of First-order ODE-IVPs § Application: chemical reactions, predator-prey models, and many others § Systems of ODEs come from the conversion of higher order ODEs into system form § Ex. 13. 6 Higher Order System of ODEs Ø Consider the equation with initial conditions The system of ODEs is Ø A system of ODEs Computer Vision & Pattern Recognition Lab.

13. 3. 1 Euler’s Method for Solving Systems of ODEs § The basic Euler method § The system of ODEs Ø Updating the function u 1 using f 1, u 2 using f 2, and u 3 using f 3. h is the same step size Computer Vision & Pattern Recognition Lab.

Ex 13. 8 § Solving a Higher Order System using Euler’s Method with initial conditions on [1, 2] with n=2(h=0. 5). at x = 3/2: at x = 2: Computer Vision & Pattern Recognition Lab.

13. 3. 2 Runge-Kutta Methods for Solving Systems of ODEs § Second order Runge-Kutta method as k and m Ø System of three ODEs Ø The values of the parameter k and m Ø The values of unknown functions Computer Vision & Pattern Recognition Lab.

System Using a Second-Order Runge-Kutta Method (Midpoint Method) § Matlab code function [ x, u ] = RK 2_sys(f, tspan, u 0, n) a = tspan(1); b = tspan(2); h = (b-a)/n; x = (a+h : b); k = h*feval(f, a, u 0)'; m = h*feval(f, a + h/2, u 0 + k/2)'; u(1, : ) = u 0 + m; for i = 1 : n -1 k=h*feval(f, x(i), u(i, : ))'; m = h*feval(f, x(i) + h/2, u(i, : ) + k/2)'; u(i+1, : ) = u(i, : ) + m; end x = [a x]; u = [u 0, u]; The indexing of the matrix for the solution u at each step is only changed Computer Vision & Pattern Recognition Lab.

Ex 13. 9 § Solving a Higher Order System using a Runge-Kutta Method Ø Interval [0, 1] of the system of ODEs with initial conditions with n=2, we find the following values for x, u 1, u 2, and u 3 Ø Matlab code function du = f_13_9(x, u) du = [u(2) ; u(3) ; x + 2*u(1) - 3*u(2) + 4*u(3)] [x, u] = RK 2_sys('f_13_9', [0 1], [4 3 2], 2) x u 1 u 2 u 3 0. 0 4. 0000 3. 0000 2. 0000 0. 5 5. 7500 4. 8750 9. 1250 1. 0 9. 3281 13. 6719 40. 9219 Computer Vision & Pattern Recognition Lab.

Ex 13. 10 § Solving a Higher Order System using a Runge-Kutta Method Ø The electrostatic potential between two concentric spheres (radius 1 and radius 2) with initial conditions u 1(1) = 10, u 2(1) = 0, u 3(1) = 0, u 4(1) = 1 on the interval [1, 2], n=2 Computer Vision & Pattern Recognition Lab.

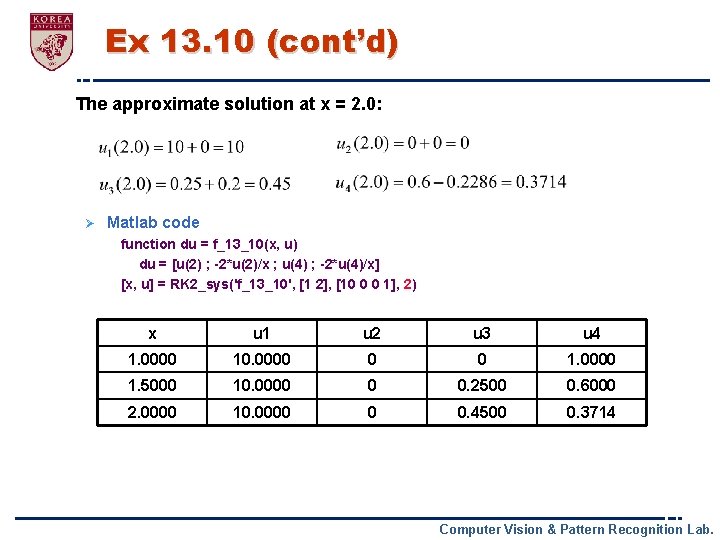
Ex 13. 10 (cont’d) The approximate solution at x = 1. 5: finding k and m again Computer Vision & Pattern Recognition Lab.

Ex 13. 10 (cont’d) The approximate solution at x = 2. 0: Ø Matlab code function du = f_13_10(x, u) du = [u(2) ; -2*u(2)/x ; u(4) ; -2*u(4)/x] [x, u] = RK 2_sys('f_13_10', [1 2], [10 0 0 1], 2) x u 1 u 2 u 3 u 4 1. 0000 10. 0000 0 0 1. 0000 1. 5000 10. 0000 0 0. 2500 0. 6000 2. 0000 10. 0000 0 0. 4500 0. 3714 Computer Vision & Pattern Recognition Lab.

Ex 13. 10 (cont’d) § n = 10 Ø Matlab code • [x, u] = RK 2_sys('f_13_10', [1 2], [10 0 0 1], 10) x u 1 u 2 u 3 U 4 1. 0000 10. 0000 0 0 1. 0000 1. 1000 10. 0000 0 0. 0900 0. 8286 1. 2000 10. 0000 0 0. 1653 0. 6976 1. 3000 10. 0000 0 0. 2293 0. 5953 1. 4000 10. 0000 0 0. 2842 0. 5139 1. 5000 10. 0000 0 0. 3319 0. 4480 1. 6000 10. 0000 0 0. 3737 0. 3941 1. 7000 10. 0000 0 0. 4107 0. 3493 1. 8000 10. 0000 0 0. 4436 0. 3117 1. 9000 10. 0000 0 0. 4730 0. 2799 2. 0000 10. 0000 0 0. 4995 0. 2527 Computer Vision & Pattern Recognition Lab.

Fourth-Order Runge-Kutta Method § Matlab code %function f(x, u); a = tspan(1); b = tspan(2); h = (b - a)/n; x = (a+h : b)'; k 1 = h*feval(f, a, u 0)'; k 2 = h*feval(f, a+h/2, u 0+k 1/2)'; k 3 = h*feval(f, a+h/2, u 0+k 2/2)'; k 4 = h*feval(f, a+h, u 0+k 3)'; u(1, : ) = u 0 + k 1/6 + k 2/3 + k 3/3 + k 4/6; for i = 1: n-1 k 1 = h*feval(f, x(i), u(i, : ))'; k 2 = h*feval(f, x(i)+h/2, u(i, : )+k 1/2)'; k 3 = h*feval(f, x(i)+h/2, u(i, : )+k 2/2)'; k 4 = h*feval(f, x(i)+h, u(i, : )+k 3)'; u(i+1, : ) = u(i, : ) + k 1/6 + k 2/3 + k 3/3 + k 4/6; end x = [a x]; u = [u 0 u]; Computer Vision & Pattern Recognition Lab.

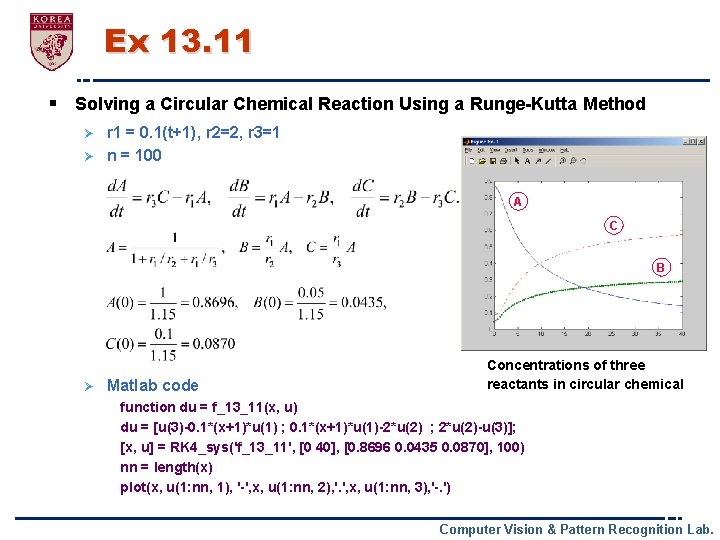
Ex 13. 11 § Solving a Circular Chemical Reaction Using a Runge-Kutta Method r 1 = 0. 1(t+1), r 2=2, r 3=1 Ø n = 100 Ø A C B Ø Matlab code Concentrations of three reactants in circular chemical function du = f_13_11(x, u) du = [u(3)-0. 1*(x+1)*u(1) ; 0. 1*(x+1)*u(1)-2*u(2) ; 2*u(2)-u(3)]; [x, u] = RK 4_sys('f_13_11', [0 40], [0. 8696 0. 0435 0. 0870], 100) nn = length(x) plot(x, u(1: nn, 1), '-', x, u(1: nn, 2), '. ', x, u(1: nn, 3), '-. ') Computer Vision & Pattern Recognition Lab.

13. 3. 3 Multistep Methods for System § The basic two-step Adams-Bashforth method y 0 is given by the initial condition Ø y 1 is found from a one-step method, such as a Runge-Kutta Ø Ø can be extended for use with a system of three ODEs u 1’ = f 1(x, u 1, u 2, u 3) u 2` = f 2(x, u 1, u 2, u 3) u 3` = f 3(x, u 1, u 2, u 3) Computer Vision & Pattern Recognition Lab.

13. 3. 3 Multistep Methods for System § The basic two-step Adams-Bashforth method (cont’d) Computer Vision & Pattern Recognition Lab.

Adams-Bashforth-Moulton § § Predictor-corrector methods Matlab code function [x, u] = ABM 3_sys(f, tspan, u 0, n) a = tspan(1); b = tspan(2); h = (b-1)/n; hh = h/12; x = (a+h: h: b)'; k = h*feval(f, a, u 0)'; m = h*feval(f, a+h/2, u 0+k/2)'; u(1, : ) = u 0+m; k = h*feval(f, x(1), u(1, : ))'; m = h*feval(f, x(1)+h/2, u(1, : )+k/2)'; u(2, : ) = u(1, : ) +m; z(2, : ) = feval(f, x(2), u(2, : ))'; uu(3, : ) = u(2, : ) + hh*(23*z(2, : ) - 16*z(1, : ) + 5*feval(f, a, u 0)'); zz = feval(f, x(3), uu(3, : ))'; u(3, : ) = u(2, : ) + h*(5*zz + 8*z(2, : ) -z(1, : )); for i = 3: n-1 z(i, : ) = feval(f, x(i), u(i, : ))'; uu(i+1, : ) = u(i, : ) + hh*(23*z(i, : ) - 16*z(i-1, : ) + 5*z(i-2, : )); zz = feval(f, x(i+1), uu(i+1, : ))'; u(i+1, : ) = u(i, : ) + hh*(5*zz + 8*z(i, : ) - z(i-1, : )); end x = [a x]; u = [u 0, u]; Computer Vision & Pattern Recognition Lab.

Ex 13. 12 Mass-and-Spring System § The vertical displacements of two masses m 1 and m 2 Spring constants s 1 and s 2 Ø Displacements x 1 and x 2 Ø m 1 m 2 X 1=0 X 2=0 Initial conditions u 1(0) = α 1, u 2(0) = α 2, u 3(0) = α 3, u 4(0) = α 4 Computer Vision & Pattern Recognition Lab.

Ex 13. 12 Mass-and-Spring System § Matlab code a = 0; b = 5; tspan = [a b]; n = 100; y 0 = [0. 5 0 0. 25 0]; global s 1 m 1 s 2 m 2 s 1 = 100; m 1 = 10; s 2 = 120; m 2 = 2; r 1 = 10; r 2 = 15; [t, y] = ABM 3_sys('f_13_12', tspan, y 0, n); [nn, mm] = size(y) %out = [t y]; plot(t(1: nn), -(r 1+y(1: nn, 1)), '-') hold on plot(t(1: nn), -(r 2+y(1: nn, 3)), '-. ') grid on plot([a b], [0 0]) hold off Displacement profiles of two masses connected by springs function du = f_13_12(t, u) global s 1 m 1 s 2 m 2 du =[u(2) ; (-s 1*u(1) + s 2*(u(3) – u(1)))/m 1 ; u(4) ; -s 2*(u(3) – u(1))/m 2 ]; ] Computer Vision & Pattern Recognition Lab.

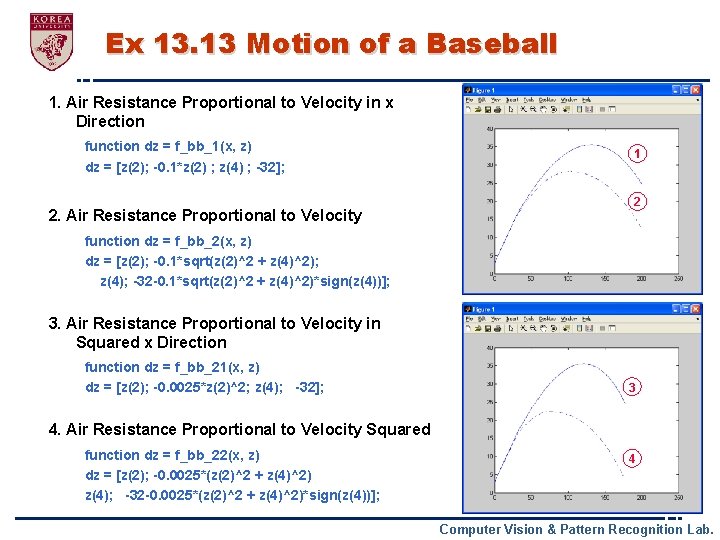
Ex 13. 13 Motion of a Baseball § Air resistance is one of the factors influencing how far a fly ball travels Inital velocity of [100, 45] Ø Acting on the horizontal component only Ø § Matlab code a = 0; b = 3; tspan = [a b]; n = 100; y 0 = [0 100 3 45]; [t, y] = ABM 3_sys('f_bb', tspan, y 0, n); [nn, mm] = size(y); out = [t y]; plot(y(1: nn, 1), y(1: nn, 3), '-') Computer Vision & Pattern Recognition Lab.

Ex 13. 13 Motion of a Baseball 1. Air Resistance Proportional to Velocity in x Direction function dz = f_bb_1(x, z) dz = [z(2); -0. 1*z(2) ; z(4) ; -32]; 2. Air Resistance Proportional to Velocity 1 2 function dz = f_bb_2(x, z) dz = [z(2); -0. 1*sqrt(z(2)^2 + z(4)^2); z(4); -32 -0. 1*sqrt(z(2)^2 + z(4)^2)*sign(z(4))]; 3. Air Resistance Proportional to Velocity in Squared x Direction function dz = f_bb_21(x, z) dz = [z(2); -0. 0025*z(2)^2; z(4); -32]; 3 4. Air Resistance Proportional to Velocity Squared function dz = f_bb_22(x, z) dz = [z(2); -0. 0025*(z(2)^2 + z(4)^2) z(4); -32 -0. 0025*(z(2)^2 + z(4)^2)*sign(z(4))]; 4 Computer Vision & Pattern Recognition Lab.

Stiff ODE and ILL-Conditioned Problem § Ill condition Ø ODE for which any error that occurs will increase, regardless of the numerical method employed u 1’ = 2 u 2 u 2` = 2 u 1 Ø General solution is u 1’ = ae 2 x+be-2 x u 2` = ae 2 x –be-2 x • The initial conditions – u 1(0) = 3, u 2(0) =-3 • We have a=0, b=3 • A component of the positive exponential will be introduced and will eventually dominate the true solution Computer Vision & Pattern Recognition Lab.

Stiff ODE and ILL-Conditioned Problem § ill condition Ø Consider the ODE Ø The general solution Ø If we take the initial condition as y(0) = 2/ 27, the exact solution is • Any error in the numerical solution process will introduce the exponential component which will eventually dominate the true solution • Parasitic solution Computer Vision & Pattern Recognition Lab.

Stiff ODE and ILL-Conditioned Problem § ill condition Ø Consider the ODE u’ = 98 u + 198 v v’ = -99 u + 199 v • Initial conditions u(0) = 1 , v(0)=0 u(t) = 2 e-t – e-100 t v(t) = -e-t + e-100 t Ø Consider the ODE • with Λ<<0 and g(t) a smooth, slowly varying function Computer Vision & Pattern Recognition Lab.

Using Matlab’s Functions § The Matlab Functions Ø ODE 23 • The Matlab functions for solving the ODE • [ T, Y ] = ODE(‘function_name’, tspan, x 0) • – ‘fuction_name’ is diffenential equations – tsapn is time duration from time t 0 to tf – x 0 is initial conditions Example function f=dfuc(t, x) f=zeros(2, 1); f(1) = 490/9*x(1) - 1996/9*x(2); f(2) = 12475*90*90*x(1)-49990/90*x(2); tspans=0: 0. 1: 4; x 0=[10 -20]; [t x] = ode 23('dfuc', tsapns, x 0); Computer Vision & Pattern Recognition Lab.

Using Matlab’s Functions § The Matlab Functions Ø ODE 23 • To solve the problem of simulating the motion of a two – link planar robot arm • See Spong and Vidyasagar, Robot Dynamic and Control, John Wiley & Sons, Inc. , New York, 1989 ( p. 145, ex 6. 4. 2) – Position, Velocity, Torques of joints • robot 2 Moment of inertia for long, slender rod I 1 = m 1*l 1^2 / 12; I 2 = m 2*l 2^2 / 12; The Mass matrix [M] d 11 = m 1*Lc 1^2 + m 2*(L 1^2 + Lc 2^2 + 2*L 1*Lc 2*cos(r 2)) + I 1 + I 2; d 12 = m 2*(Lc 2^2 + L 1*Lc 2*cos(r 2)) + I 2; d 21 = d 12; d 22 = m 2*Lc 2^2 + I 2; Computer Vision & Pattern Recognition Lab.

Using Matlab’s Functions § The Matlab Functions Ø ODE 23 • robot 2_1 Initialize Calculate each parameters Plot each parameters Computer Vision & Pattern Recognition Lab.

Using Matlab’s Functions § The Matlab Functions Ø ODE 23 • To solve the problem of simulating the motion of a two – link planar robot arm • robot 2 Computer Vision & Pattern Recognition Lab.

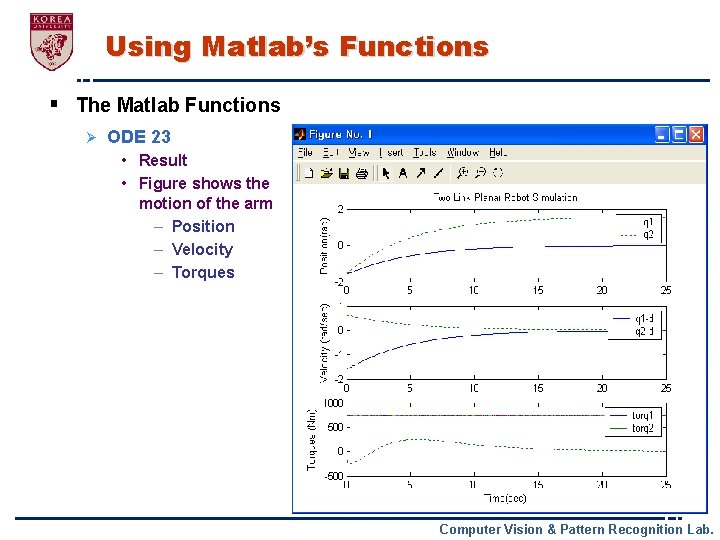
Using Matlab’s Functions § The Matlab Functions Ø ODE 23 • Result • Figure shows the motion of the arm – Position – Velocity – Torques Computer Vision & Pattern Recognition Lab.