Systems of Linear Measure Technology Exploration Granite Oaks

Systems of Linear Measure Technology Exploration Granite Oaks Middle School Mr. Frank

Table of Contents n Definitions n n n Linear Measure Scale n n n Fractions & Decimals Conversions How to Read a Ruler Example Measuring Examples Your turn to Practice

n Measure Definitions Specifying a distance or length n Accurate measurements are critical in planning a project n n Linear Straight lines n Linear measure is the measurement of distance n n Scale Are constantly used in drafting n Used to make measurements that are full size, larger than, or smaller than the final product n

Why Measure? n Accurate measurement is critical for success! Estimation of materials n So that all the pieces fit properly n n Accuracy changes for each project While machining, 1/100 of an inch may be necessary n While building a house 1/16” may be enough n n We measure our projects so that they are built to the same specifications of their design

Fractions & Decimals n n Fractions tend to be less accurate than decimals Fractions are commonly used for architecture and construction projects n n n Examples- Houses, trailers, fences, etc… Decimals contain an implied accuracy Decimals are used in engineering projects Tight tolerances require great accuracy & precision n Decimals are used in mechanical drawings n Examples- Bearings, Gears, Motors, etc… n

Fractions & Decimals n Fractions Examples are ¼”; ½”; etc… n Denominator (the number on bottom) n n Tells us how many divisions in an inch n n n ½ = 2 divisions to make an inch ¼ = 4 divisions to make an inch Numerator (the number on top) Tells us how many of those divisions are used n ¾ means that 3 of the 4 divisions are used n n Fractional measures are always reduced n We would say 5/8” not 10/16”

Conversions n We can go from fractions to decimals n n We can go from decimals to fractions n n n We simply divide the fraction 1/8” = 1÷ 8 = 0. 125” 0. 0625” = 1/16” We generally use decimals for tight tolerances and high accuracy needs We generally use feet and inches for construction projects and general building

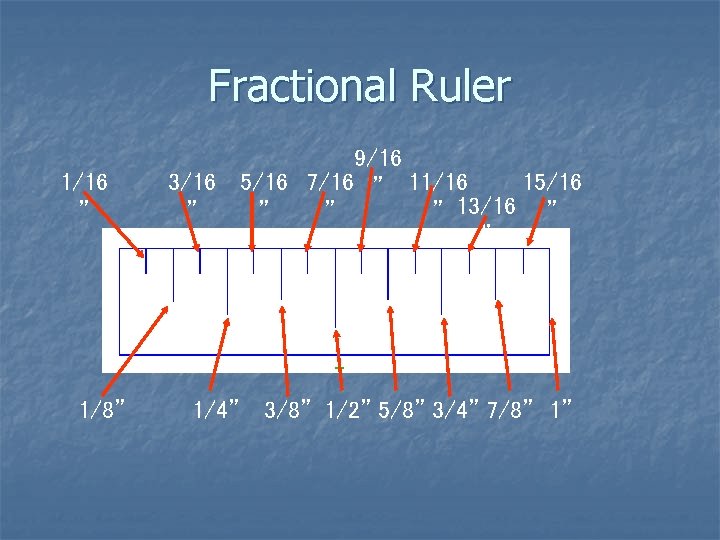
How to Read a Ruler n n n Every mark on our rulers are 1/16” Count the number of marks The count goes in the numerator. n n The denominator will always be 16 If the count is an even number, it will need to be reduced i. e. 12/16” = 6/8” = ¾” n i. e. 9/16” can not be reduced n

Fractional Ruler 1/16 ” 1/8” 9/16 3/16 5/16 7/16 ” 11/16 15/16 ” ” 13/16 ” ” 1/4” 3/8” 1/2” 5/8” 3/4” 7/8” 1”

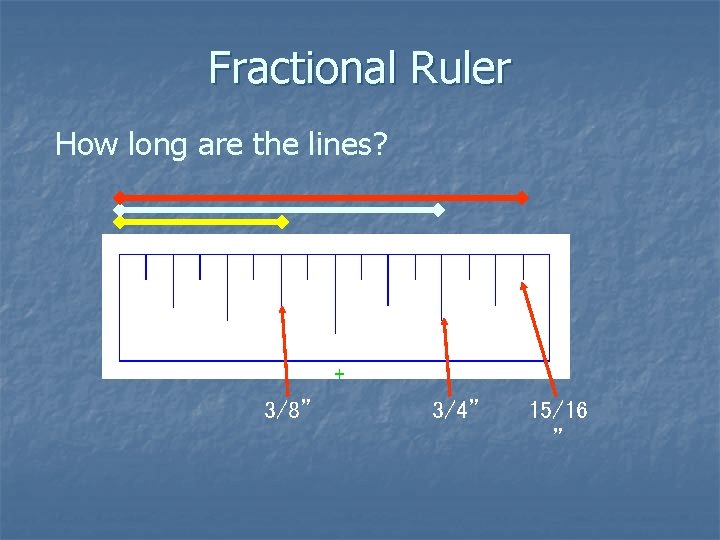
Fractional Ruler How long are the lines? 3/8” 3/4” 15/16 ”

Fractional Ruler What measurement is identified by the pointer? ¼” 11/16” 7/16”

Your Turn to Practice n n Complete each handout using a pencil Some of the handouts require a standard ruler. Obtain a standard ruler from your instructor. Some of the exercises require an enlarged ruler. That is included as needed in your handouts Read and follow all directions for full credit