Systems of Linear Equations Using a Graph to

Systems of Linear Equations Using a Graph to Solve

Warmup

What is a System of Linear Equations? A system of linear equations is simply two or more linear equations using the same variables. If the system has a solution, then the solution must be an ordered pair (x , y) where x and y make both equations true at the same time. If the lines are parallel, there will be no solutions. If the lines are the same, there will be an infinite number of solutions.

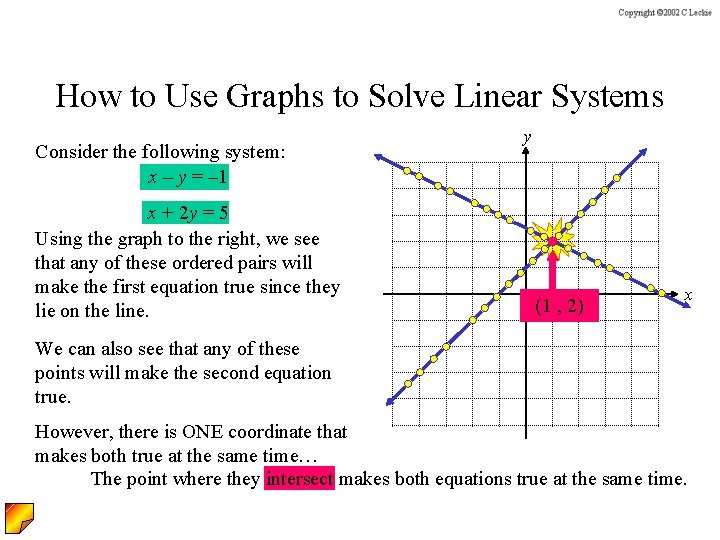
How to Use Graphs to Solve Linear Systems Consider the following system: x – y = – 1 x + 2 y = 5 Using the graph to the right, we see that any of these ordered pairs will make the first equation true since they lie on the line. y (1 , 2) x We can also see that any of these points will make the second equation true. However, there is ONE coordinate that makes both true at the same time… The point where they intersect makes both equations true at the same time.

• If the lines cross once, there will be one solution. • If the lines are parallel, there will be no solutions. • If the lines are the same, there will be an infinite number of solutions.

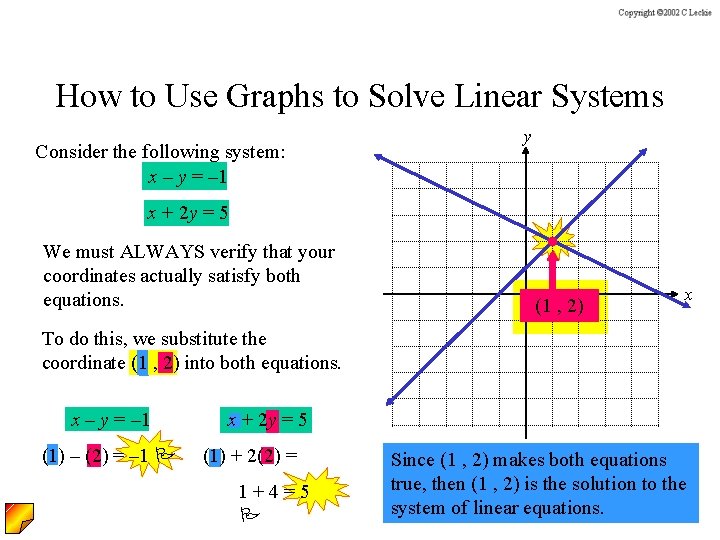
How to Use Graphs to Solve Linear Systems Consider the following system: x – y = – 1 y x + 2 y = 5 We must ALWAYS verify that your coordinates actually satisfy both equations. (1 , 2) x To do this, we substitute the coordinate (1 , 2) into both equations. x – y = – 1 (1) – (2) = – 1 x + 2 y = 5 (1) + 2(2) = 1+4=5 Since (1 , 2) makes both equations true, then (1 , 2) is the solution to the system of linear equations.

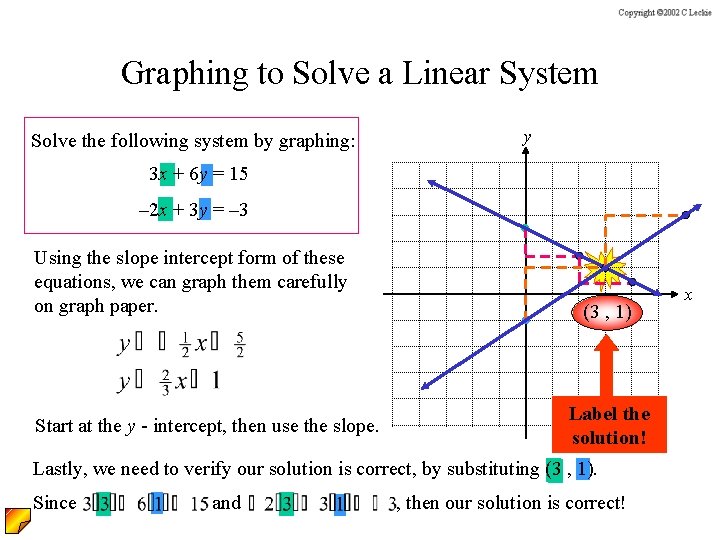
Graphing to Solve a Linear System Solve the following system by graphing: 3 x + 6 y = 15 – 2 x + 3 y = – 3 Start with 3 x + 6 y = 15 Subtracting 3 x from both sides yields 6 y = – 3 x + 15 Before you graph, make sure the equation is in slope - intercept form. To put the equations in slope intercept form, we must solve both equations for y. Dividing everything by 6 gives us… Similarly, we can add 2 x to both sides and then divide everything by 3 in the second equation to get Now, we must graph these two equations.

Graphing to Solve a Linear System Solve the following system by graphing: y 3 x + 6 y = 15 – 2 x + 3 y = – 3 Using the slope intercept form of these equations, we can graph them carefully on graph paper. Start at the y - intercept, then use the slope. (3 , 1) Label the solution! Lastly, we need to verify our solution is correct, by substituting (3 , 1). Since and , then our solution is correct! x

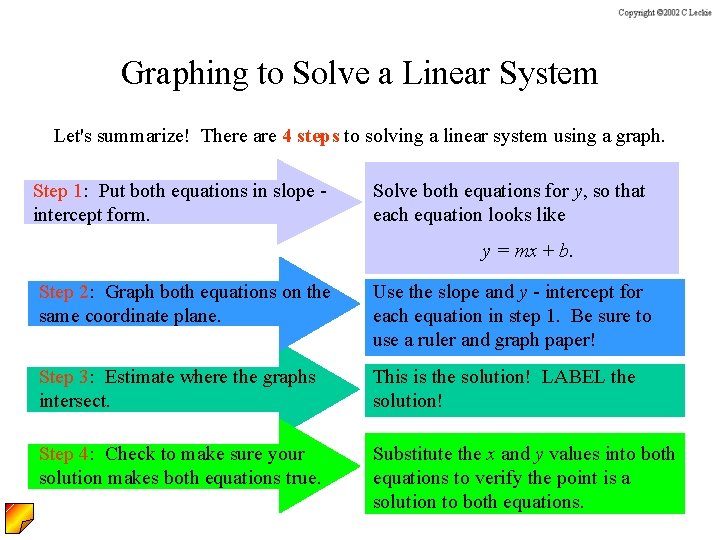
Graphing to Solve a Linear System Let's summarize! There are 4 steps to solving a linear system using a graph. Step 1: Put both equations in slope intercept form. Solve both equations for y, so that each equation looks like y = mx + b. Step 2: Graph both equations on the same coordinate plane. Use the slope and y - intercept for each equation in step 1. Be sure to use a ruler and graph paper! Step 3: Estimate where the graphs intersect. This is the solution! LABEL the solution! Step 4: Check to make sure your solution makes both equations true. Substitute the x and y values into both equations to verify the point is a solution to both equations.

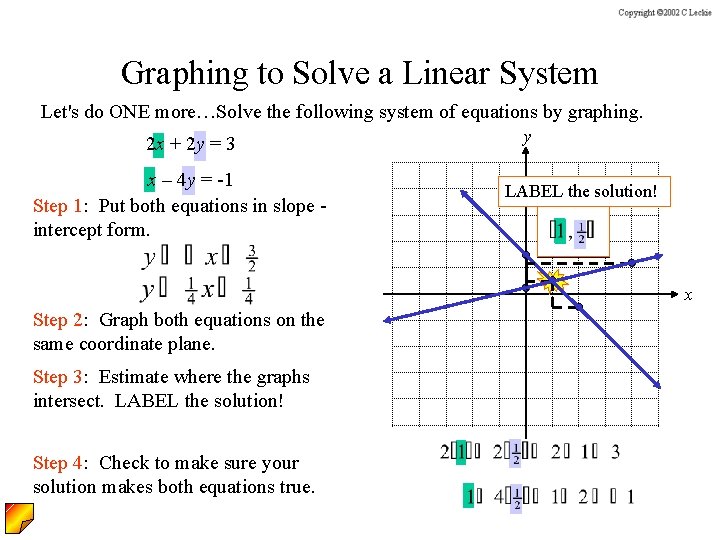
Graphing to Solve a Linear System Let's do ONE more…Solve the following system of equations by graphing. 2 x + 2 y = 3 x – 4 y = -1 Step 1: Put both equations in slope intercept form. y LABEL the solution! x Step 2: Graph both equations on the same coordinate plane. Step 3: Estimate where the graphs intersect. LABEL the solution! Step 4: Check to make sure your solution makes both equations true.

Exit Ticket • What are three different possibilities for solutions when solving a system of equations?