Systems of Equations OBJECTIVES To understand what a

Systems of Equations

OBJECTIVES • To understand what a system of equations is. • Be able to solve a system of equations from graphing the equations • Determine whether the system has one solution, no solution, or an infinite amount of solutions. • Be able to graph equations without using a graphing calculator.

Defining a System of Equations • A grouping of 2 or more equations, containing one or more variables. x+y=2 2 y = x + 2 2 x + y = 5 x - 7 6 x - y = 5

How do we “solve” a system of equations? ? ? • By finding the point where two or more equations, intersect. x+y=6 y = 2 x 6 Point of intersection 4 2 1 2

How do we “solve” a system of equations? ? ? • By finding the point where two or more equations, intersect. x+y=6 y = 2 x 6 (2, 4) 4 2 1 2

ax + by = c 2 x + 3 y = 6 -2 x 3 y = 6 - 2 x 3 3 3 2 y=2 x 3 2 y=- x+2 3 ax + by = c (Standard Form) WE WANT THIS FORM!!! y = mx + b (Slope- Intercept)

Non-Unique Solutions No Solution: • when lines of a graph are parallel • since they do not intersect, there is no solution • the slopes are the same and the equation must be in slope-intercept form

Example of No Solution 2 x+y=8 y=-2 x-3 Remember when graphing the equations need to be in slope intercept form!!!

Non-Unique Solutions Infinite Solutions: • a pair of equations that have the same slope and y-intercept. • also call a Dependent System

Example of Infinite Solutions 2 x+4 y=8 4 x+8 y=16

Unique Solutions One Solution: • the lines of two equations intersect • also called an Independent System

Graphing Systems in Slope-Intercept Form • 2 y + x = 8 y = 2 x + 4 Steps: 1. Get both equations in slope-intercept form 2. Find the slope and y intercept of eq. 1 then graph 3. Find the slope and y intercept of eq. 2 then graph 4. Find point of intersection

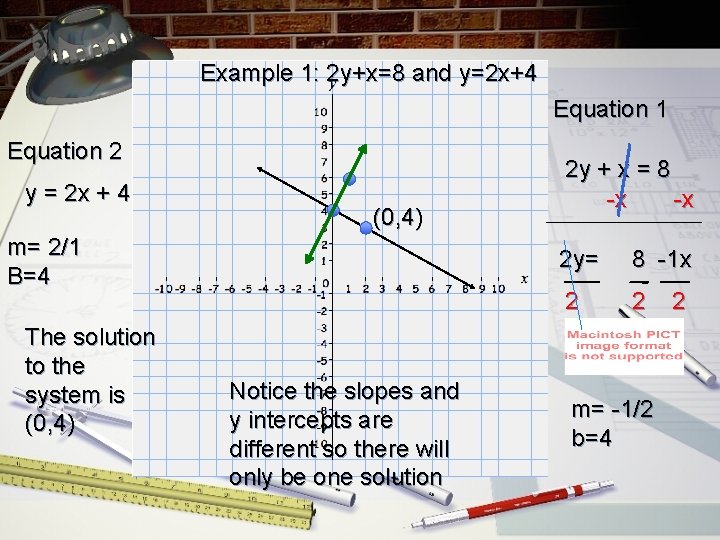
Example 1: 2 y+x=8 and y=2 x+4 Equation 1 Equation 2 y = 2 x + 4 (0, 4) m= 2/1 B=4 The solution to the system is (0, 4) Notice the slopes and y intercepts are different so there will only be one solution 2 y + x = 8 -x -x 2 y= 8 -1 x 2 2 m= -1/2 b=4 2

Example 2: y=-6 x+8 and y+6 x=8 Equation 1 Equation 2 y=-6 x+8 y+6 x=8 b=8 -6 x y=8 -6 x b=8 m=-6(down) 1(right) Infinite Solution m=-6(down) 1(right) Notice both equations have the same intercept and slope. This means all the points are solutions.

Example 3: x-5 y=10 and -5 y=-x+40 Equation 1 Equation 2 x-5 y=10 -x -x -5 y=-x+40 __ __ ___ -5 -5 -5 -__ 5 y=10 -1 x __ __ -5 -5 -5 b=-8 m=1/5 The slopes are the same with different intercepts so the lines are parallel b=-2 m=1/5 No Solution

You Try Examples Determine whether the following equations have one, none, or infinite solutions by graphing on the graph paper provided. 1) 2) 2 y= x-1 3 y=3 ANS: One Solution (6, 3) ANS: Infinite Solutions 3) x + 2 y = 6 x + 2 y = 8 ANS: No Solution

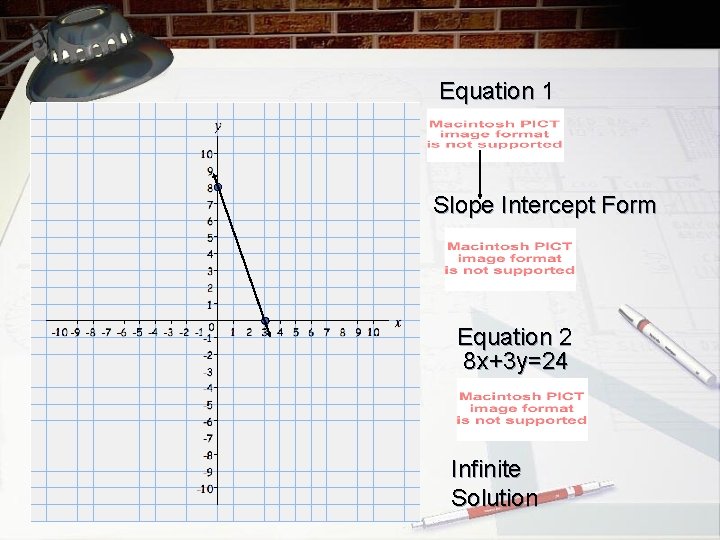
Equation 1 Slope Intercept Form Equation 2 8 x+3 y=24 Infinite Solution

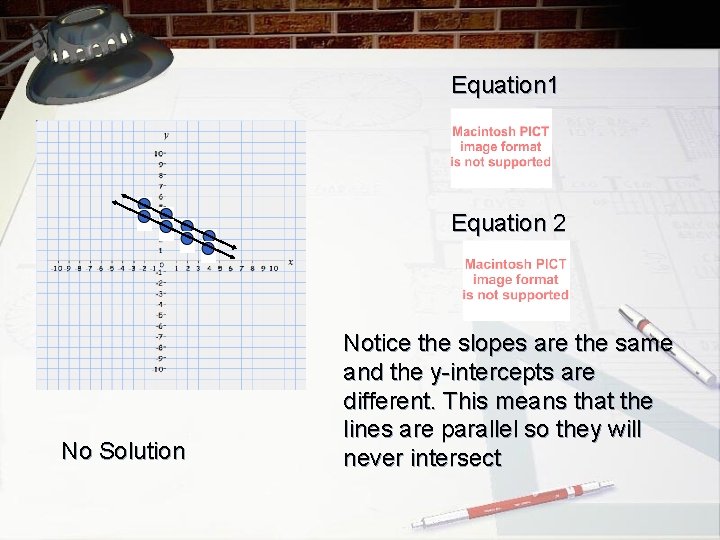
Equation 1 Equation 2 No Solution Notice the slopes are the same and the y-intercepts are different. This means that the lines are parallel so they will never intersect

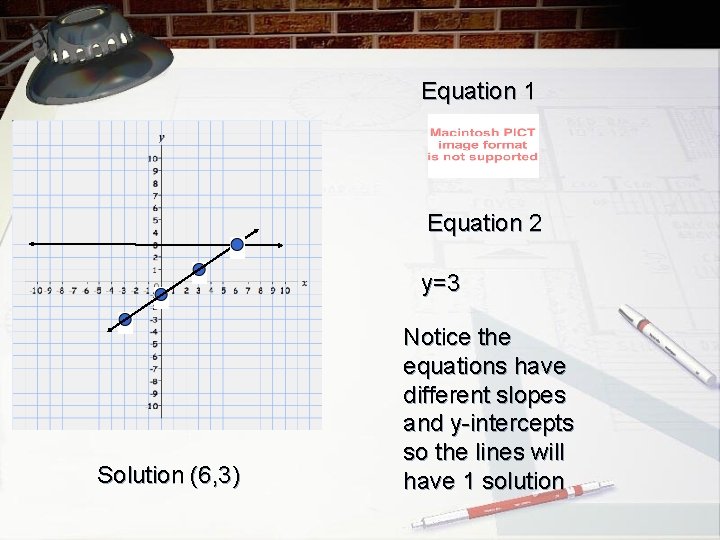
Equation 1 Equation 2 y=3 Solution (6, 3) Notice the equations have different slopes and y-intercepts so the lines will have 1 solution

Algebraically determine if a point is a solution We must always verify a proposed solution algebraically. We propose (1, 6) as a solution, so now we plug it in to both equations to see if it works: y = 6 x and 6 = 6(1) and (6)= 6 and y = 2 x + 4, 6=2(1)+4, 6= 6. Yes, (1, 6) Satisfies both equations!

Algebraically determine if a point is a solution • Determine if (2, 12) is a solution to the system. • y=6 x and y=2 x+4 • 12=6(2) and 12=2(2)+4 • 12=12 and 12=8 • Yes No • (2, 12) is NOT a solution to the system