Systems of Equations OBJECTIVES a To understand what

Systems of Equations

OBJECTIVES a. To understand what a system of equations is. b. Be able to solve a system of equations from graphing the equations c. Determine whether the system has one solution, no solution, or an infinite amount of solutions. d. Be able to graph equations without using a graphing calculator.

Defining a System of Equations a. A grouping of 2 or more equations, containing one or more variables. x+y=2 2 x + y = 5 2 y = x + 2 y = 5 x - 7 6 x - y = 5

How do we “solve” a system of equations? ? ? a. By finding the point where two or more equations, intersect. x+y=6 y = 2 x 6 Point of intersection 4 2 1 2

How do we “solve” a system of equations? ? ? a. By finding the point where two or more equations, intersect. x+y=6 y = 2 x 6 (2, 4) 4 2 1 2

PRACTICE WORKSHEET… LET’S GO ONLINE AND USE THE GRAPHER… !!!!
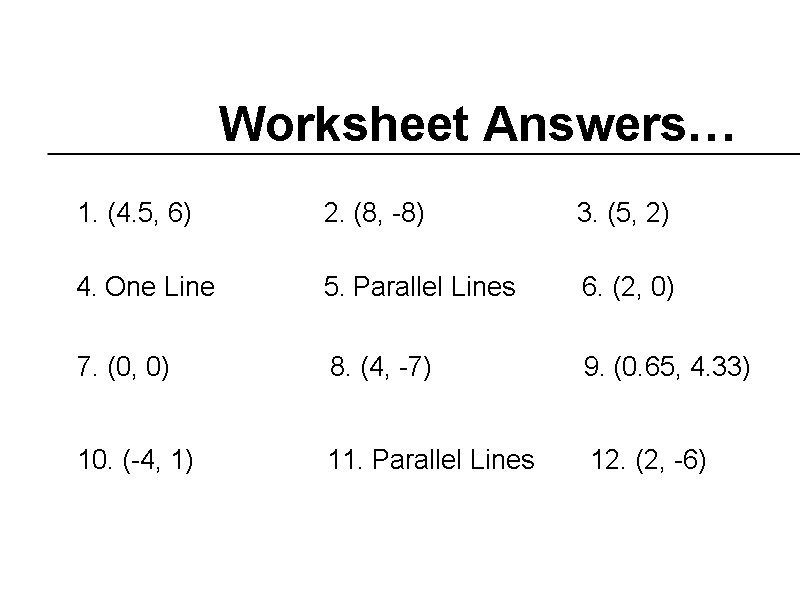
Worksheet Answers… 1. (4. 5, 6) 2. (8, -8) 3. (5, 2) 4. One Line 5. Parallel Lines 6. (2, 0) 7. (0, 0) 8. (4, -7) 9. (0. 65, 4. 33) 10. (-4, 1) 11. Parallel Lines 12. (2, -6)

ax + by = c 2 x + 3 y = 6 -2 x 3 y = 6 - 2 x 3 3 3 2 y=2 - x 3 2 y = - + 2 x 3 ax + by = c (Standard Form) WE WANT THIS FORM!!! y = mx + b (Slope- Intercept)

ax + by = c NOTE: The equation ax + by = c is just another form of a linear equation.

Non-Unique Solutions No Solution: a. when lines of a graph are parallel a. since they do not intersect, there is no solution a. also called an Inconsistent System
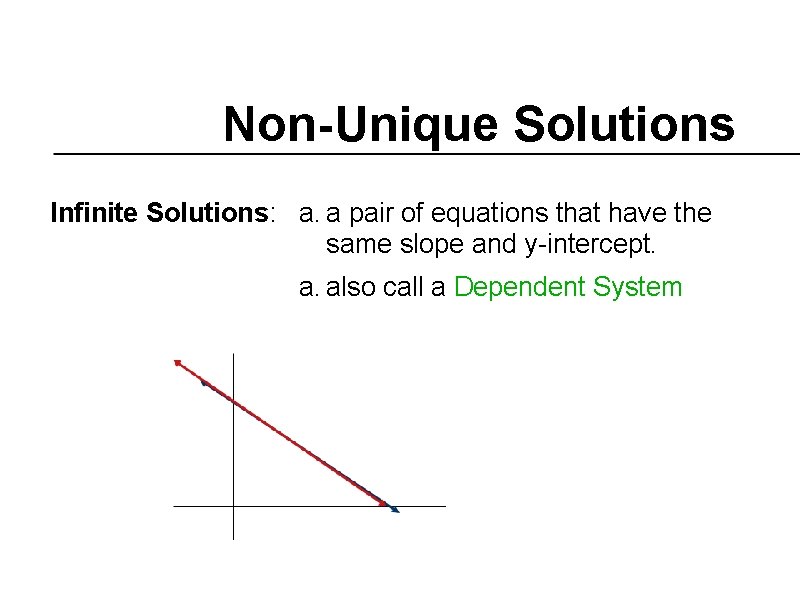
Non-Unique Solutions Infinite Solutions: a. a pair of equations that have the same slope and y-intercept. a. also call a Dependent System

Non-Unique Solutions One Solution: a. the lines of two equations intersect a. also called an Independent System

Examples… Determine whether the following have one, none, or infinite solutions by looking at the slope and y-intercepts 1) 2 y + x = 8 2) y = -6 x + 8 y = 2 x + 4 y + 6 x = 8 ANS: One Solution ANS: Infinite Solutions 3) x - 5 y = 10 -5 y = -x +6 ANS: No Solution

Graphing Manually Using the y-intercept and the linear slope to graph the equation: y = 2 x + 4
Graphing Manually Using the y-intercept and the linear slope to graph the equation: y = 2 x + 4 1. Plot the y-intercept
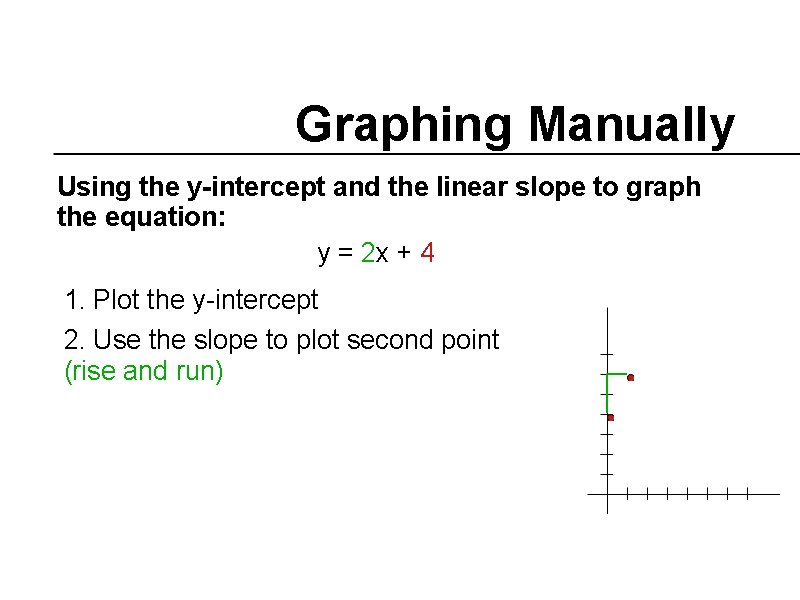
Graphing Manually Using the y-intercept and the linear slope to graph the equation: y = 2 x + 4 1. Plot the y-intercept 2. Use the slope to plot second point (rise and run)
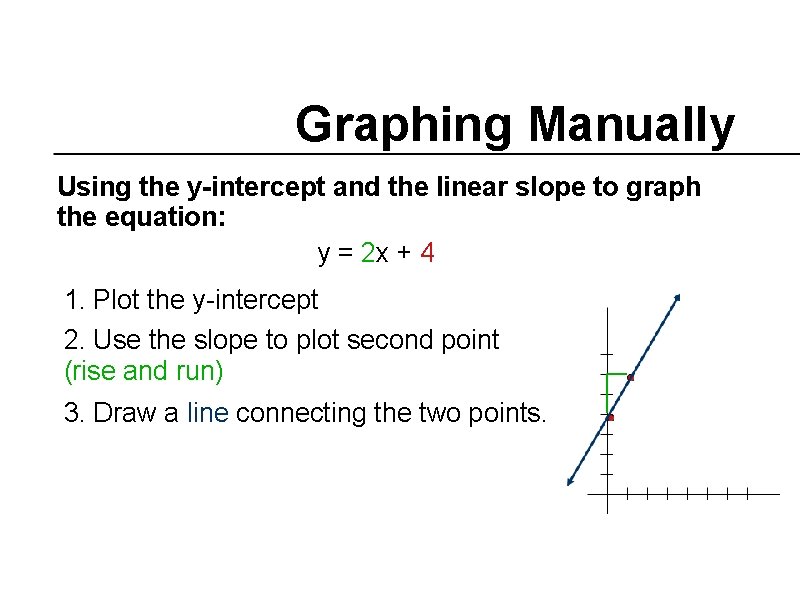
Graphing Manually Using the y-intercept and the linear slope to graph the equation: y = 2 x + 4 1. Plot the y-intercept 2. Use the slope to plot second point (rise and run) 3. Draw a line connecting the two points.

Graphing Manually cont. Plot two points by Solving for y by entering random values for x. 2 x + 3 y = 4
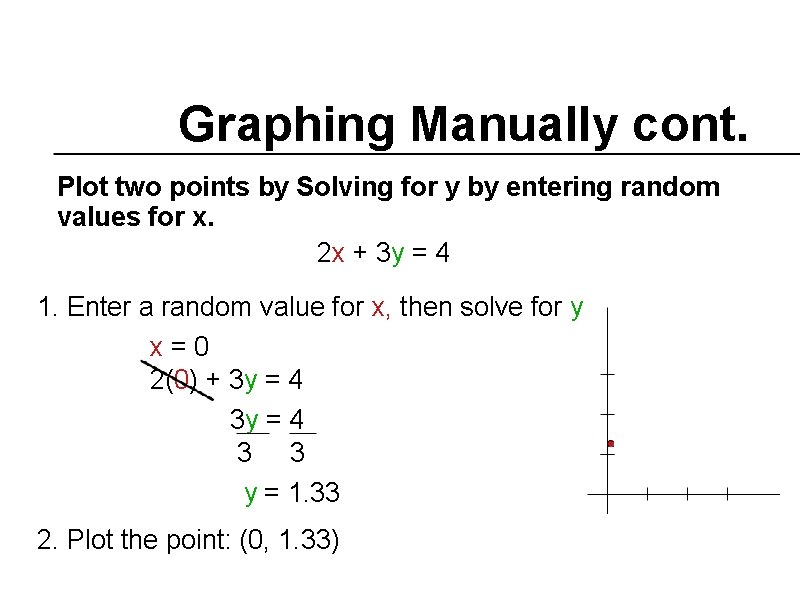
Graphing Manually cont. Plot two points by Solving for y by entering random values for x. 2 x + 3 y = 4 1. Enter a random value for x, then solve for y x=0 2(0) + 3 y = 4 3 3 y = 1. 33 2. Plot the point: (0, 1. 33)
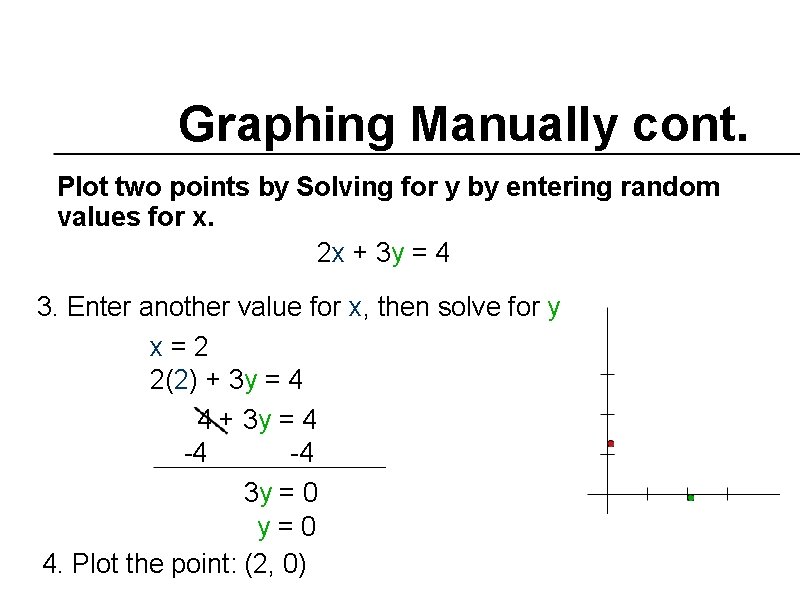
Graphing Manually cont. Plot two points by Solving for y by entering random values for x. 2 x + 3 y = 4 3. Enter another value for x, then solve for y x=2 2(2) + 3 y = 4 4 + 3 y = 4 -4 -4 3 y = 0 y=0 4. Plot the point: (2, 0)
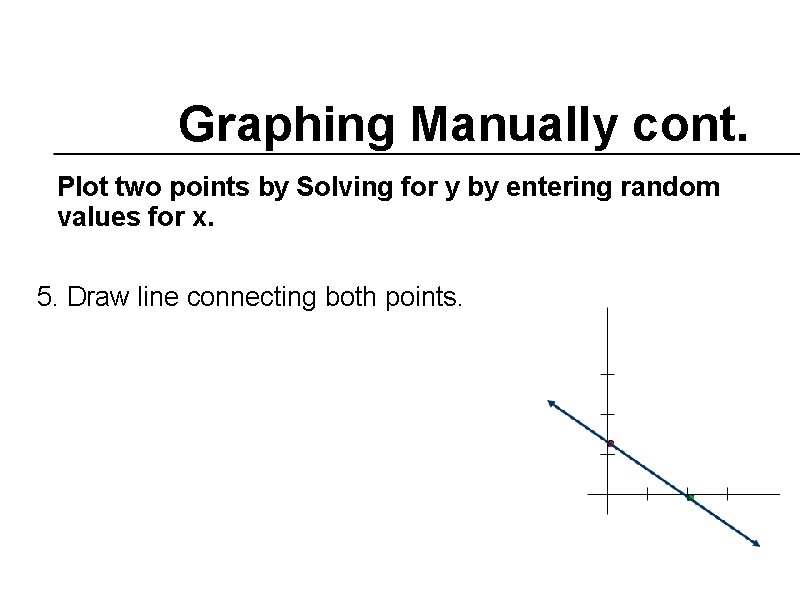
Graphing Manually cont. Plot two points by Solving for y by entering random values for x. 5. Draw line connecting both points.

more Examples Determine whether the following equations have one, none, or infinite solutions. If “one solution” graph it and give the point of intersection. NO GRAPHER 1) 2) 2 y=x-1 3 y=3 ANS: One Solution (6, 3) ANS: Infinite Solutions 3) x + 2 y = 6 x + 2 y = 8 ANS: No Solution
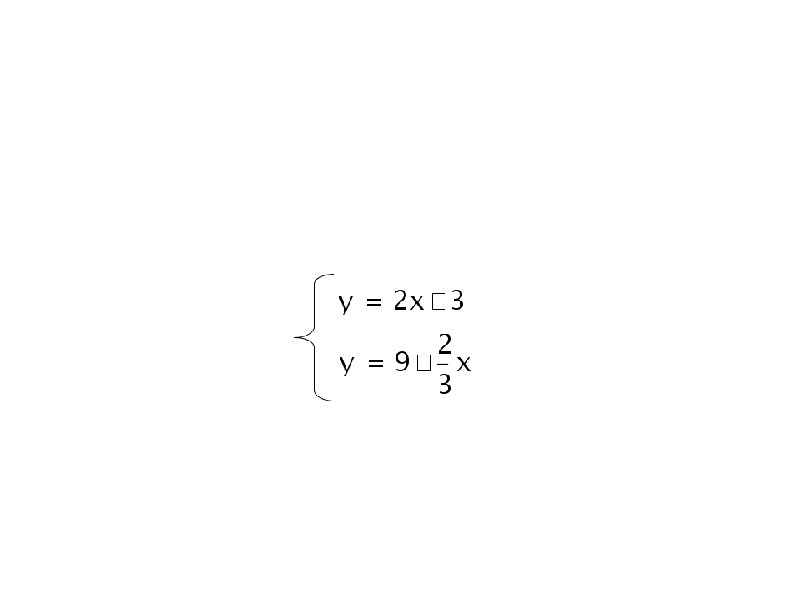
- Slides: 23