Systems Engineering Program Department of Engineering Management Information

Systems Engineering Program Department of Engineering Management, Information and Systems EMIS 7370/5370 STAT 5340 : PROBABILITY AND STATISTICS FOR SCIENTISTS AND ENGINEERS Special Continuous Probability Distributions -Exponential Distribution -Weibull Distribution Dr. Jerrell T. Stracener, SAE Fellow Leadership in Engineering 1 Stracener_EMIS 7370/STAT 5340_Fall 08_09. 25. 08

Exponential Distribution 2

The Exponential Model - Definition A random variable X is said to have the Exponential Distribution with parameters , where > 0, if the probability density function of X is: , for 0 , elsewhere 3

Properties of the Exponential Model • Probability Distribution Function for < 0 for 0 *Note: the Exponential Distribution is said to be without memory, i. e. • P(X > x 1 + x 2 | X > x 1) = P(X > x 2) 4

Properties of the Exponential Model • Mean or Expected Value • Standard Deviation 5

Exponential Model - Example Suppose the response time X at a certain on-line computer terminal (the elapsed time between the end of a user’s inquiry and the beginning of the system’s response to that inquiry) has an exponential distribution with expected response time equal to 5 sec. (a) What is the probability that the response time is at most 10 seconds? (b) What is the probability that the response time is between 5 and 10 seconds? (c) What is the value of x for which the probability of exceeding that value is 1%? 6

Exponential Model - Example The E(X) = 5=θ, so λ = 0. 2. The probability that the response time is at most 10 sec is: or P (X>10) = 0. 135 The probability that the response time is between 5 and 10 sec is: 7

Exponential Model - Example The value of x for which the probability of exceeding x is 1%: 8

Weibull Distribution 9

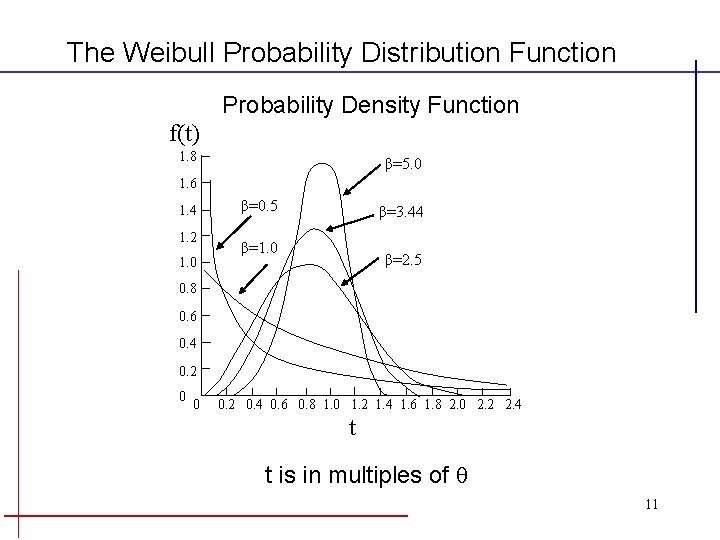
The Weibull Probability Distribution Function • Definition - A random variable X is said to have the Weibull Probability Distribution with parameters and , where > 0 and > 0, if the probability density function of is: , for 0 , elsewhere Where, is the Shape Parameter, is the Scale Parameter. Note: If = 1, the Weibull reduces to the Exponential Distribution. 10

The Weibull Probability Distribution Function Probability Density Function f(t) 1. 8 β=5. 0 1. 6 1. 4 1. 2 1. 0 β=0. 5 β=3. 44 β=1. 0 β=2. 5 0. 8 0. 6 0. 4 0. 2 0 0 0. 2 0. 4 0. 6 0. 8 1. 0 1. 2 1. 4 1. 6 1. 8 2. 0 2. 2 2. 4 t t is in multiples of 11

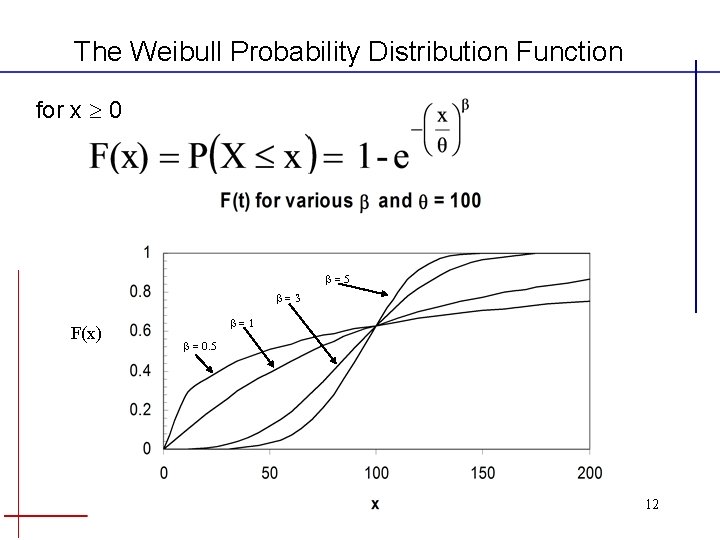
The Weibull Probability Distribution Function for x 0 =5 =3 F(x) =1 = 0. 5 12

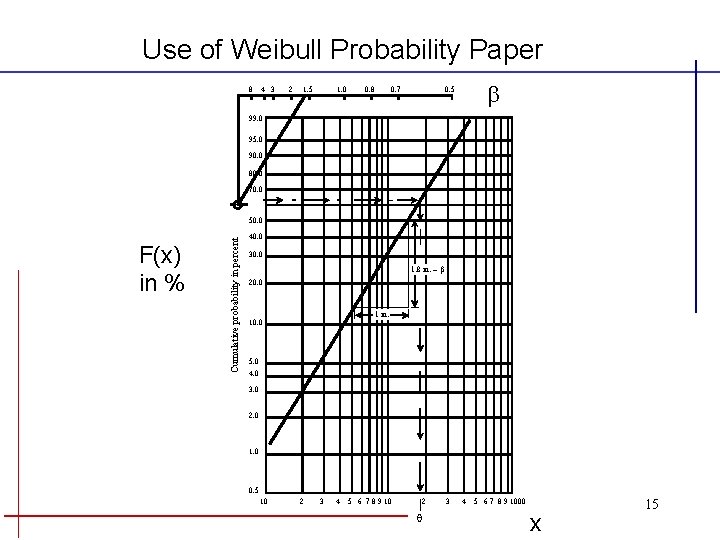
Weibull Probability Paper (WPP) • Derived from double logarithmic transformation of the Weibull Distribution Function. • Of the form where • Any straight line on Weibull Probability paper is a Weibull Probability Distribution Function with slope, and intercept, - ln , where the ordinate is ln{ln(1/[1 -F(t)])} the abscissa is ln t. 13

Weibull Probability Paper (WPP) Weibull Probability Paper links http: //perso. easynet. fr/~philimar/graphpapeng. htm http: //www. weibull. com/GPaper/index. htm 14

Use of Weibull Probability Paper 8 4 3 2 1. 5 1. 0 0. 8 0. 7 0. 5 99. 0 95. 0 90. 0 80. 0 70. 0 F(x) in % Cumulative probability in percent 50. 0 40. 0 30. 0 1. 8 in. = 20. 0 1 in. 10. 0 5. 0 4. 0 3. 0 2. 0 1. 0 0. 5 10 2 3 4 5 6 7 8 9 1000 x 15

Properties of the Weibull Distribution • 100 pth Percentile and, in particular • Mean or Expected Value Note: See the Gamma Function Table to obtain values of (a) 16

Properties of the Weibull Distribution • Standard Deviation of X where 17

The Gamma Function Values of the Gamma Function 18

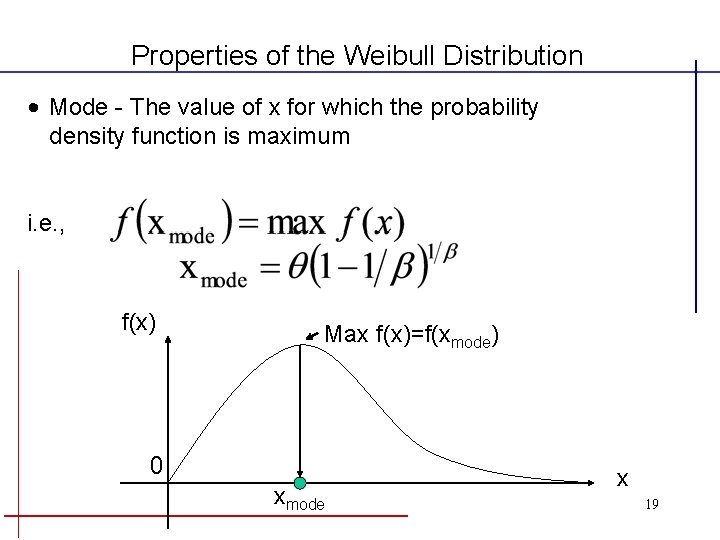
Properties of the Weibull Distribution • Mode - The value of x for which the probability density function is maximum i. e. , f(x) Max f(x)=f(xmode) 0 xmode x 19

Weibull Distribution - Example Let X = the ultimate tensile strength (ksi) at -200 degrees F of a type of steel that exhibits ‘cold brittleness’ at low temperatures. Suppose X has a Weibull distribution with parameters = 20, and = 100. Find: (a) P( X 105) (b) P(98 X 102) (c) the value of x such that P( X x) = 0. 10 20

Weibull Distribution - Example Solution (a) P( X 105) = F(105; 20, 100) (b) P(98 X 102) = F(102; 20, 100) - F(98; 20, 100) 21

Weibull Distribution - Example Solution (c) P( X x) = 0. 10 P( X x) Then 22

Weibull Distribution - Example The random variable X can modeled by a Weibull distribution with = ½ and = 1000. The spec time limit is set at x = 4000. What is the proportion of items not meeting spec? 23

Weibull Distribution - Example The fraction of items not meeting spec is That is, all but about 13. 53% of the items will not meet spec. 24