Systems Architecture Lecture 12 Design of the MIPS

Systems Architecture Lecture 12: Design of the MIPS ALU Jeremy R. Johnson Anatole D. Ruslanov William M. Mongan Some or all figures from Computer Organization and Design: The Hardware/Software Approach, Third Edition, by David Patterson and John Hennessy, are copyrighted material (COPYRIGHT 2004 MORGAN KAUFMANN PUBLISHERS, INC. ALL RIGHTS RESERVED). Lec 12 Systems Architecture 1

Introduction • Objective: To learn what operations are performed by the Arithmetic Logic Unit (ALU) and to learn how the MIPS ALU is implemented. • Topics – – – MIPS logical operations Full Adder 1 -But ALU The design of the MIPS 32 -Bit ALU Overflow and Overflow Detection Carry Lookahead Lec 12 Systems Architecture 2

Addition and Subtraction • Carry-ripple adder 0000 0111 + 0000 0110 0000 1101 0000 0111 - 0000 0110 0001 Lec 12 0000 0111 +1111 1010 0001 Systems Architecture 0000 0110 - 0000 0111 1111 0000 0110 + 1111 1001 1111 3

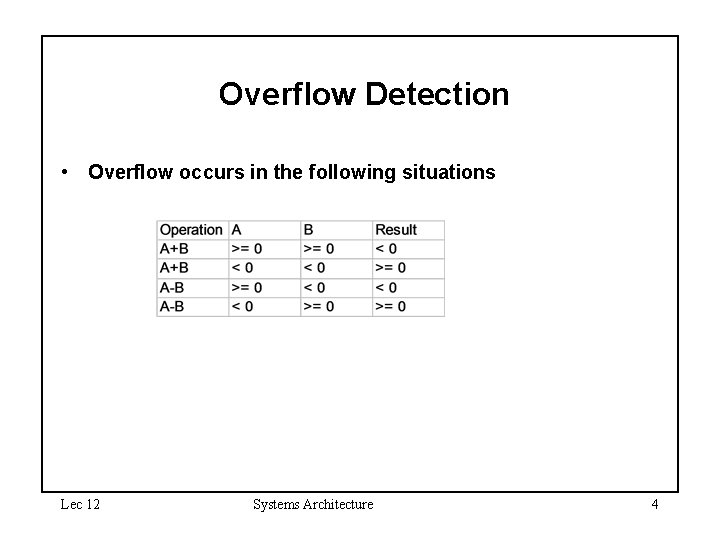
Overflow Detection • Overflow occurs in the following situations Lec 12 Systems Architecture 4

Logical Operations • • Shift left << Shift right >> Shift right arithmetic Bitwise and & Bitwise or | Bitwise complement (not) ~ Exclusive or ^ Lec 12 Systems Architecture sll sra and, andi or, ori not (pseudo) xor, xori 5

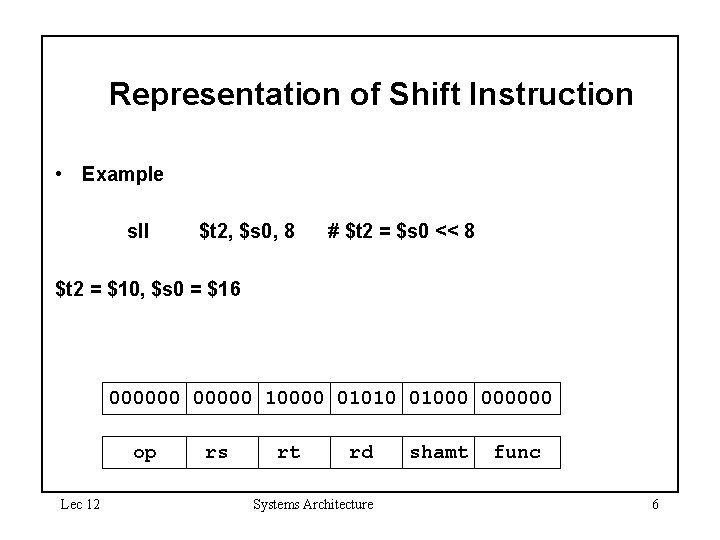
Representation of Shift Instruction • Example sll $t 2, $s 0, 8 # $t 2 = $s 0 << 8 $t 2 = $10, $s 0 = $16 000000 10000 01010 01000 000000 op Lec 12 rs rt rd Systems Architecture shamt func 6

Example use of Logical Operations Int data; struct { unsigned int ready: 1; unsigned int enable: 1; | unsigned int received. Byte: 8; } receiver; … data = receiver. received. Byte; receiver. ready = 0; receiver. enable = 1; Lec 12 • Assume data in $s 0 • receiver in $s 1 9 2 1 0 received. Byte | enable | ready Systems Architecture • sll $s 0, $s 1, 22 • srl $s 0, 24 • andi $s 1, 0 xfffe • ori $s 1, 0 x 0002 7

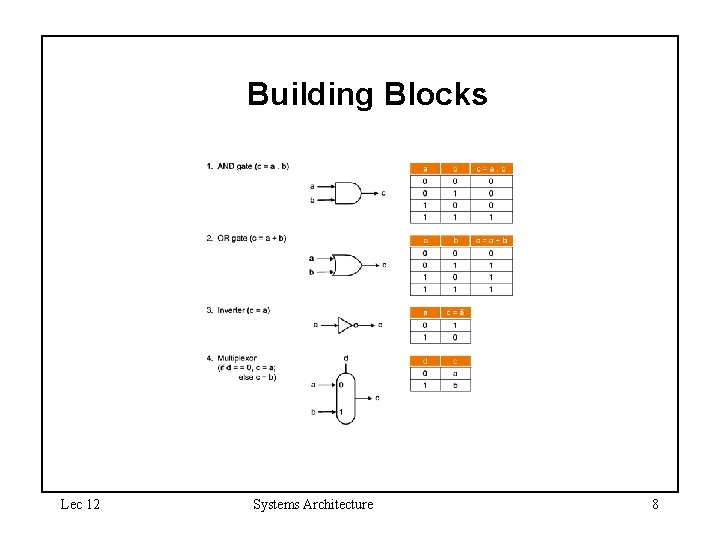
Building Blocks Lec 12 Systems Architecture 8

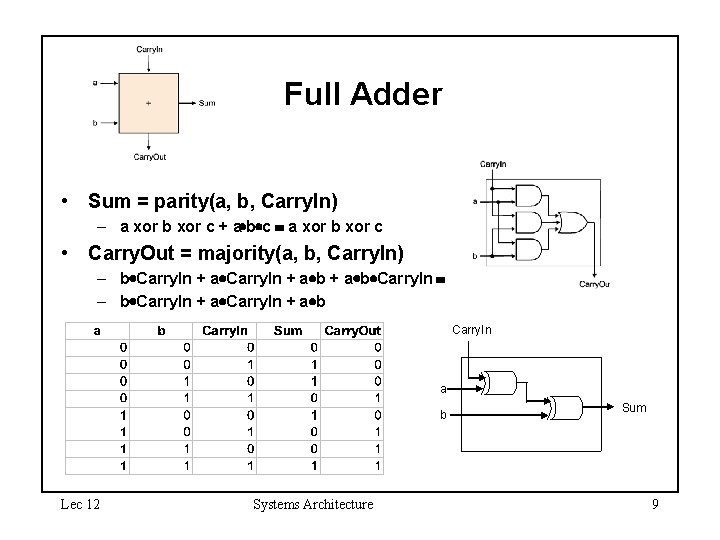
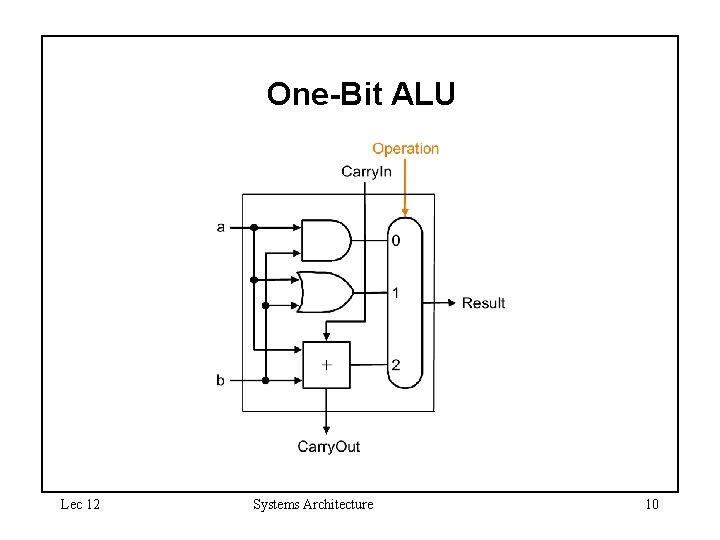
Full Adder • Sum = parity(a, b, Carry. In) – a xor b xor c + a b c a xor b xor c • Carry. Out = majority(a, b, Carry. In) – b Carry. In + a b Carry. In – b Carry. In + a b Carry. In a b Lec 12 Systems Architecture Sum 9

One-Bit ALU Lec 12 Systems Architecture 10

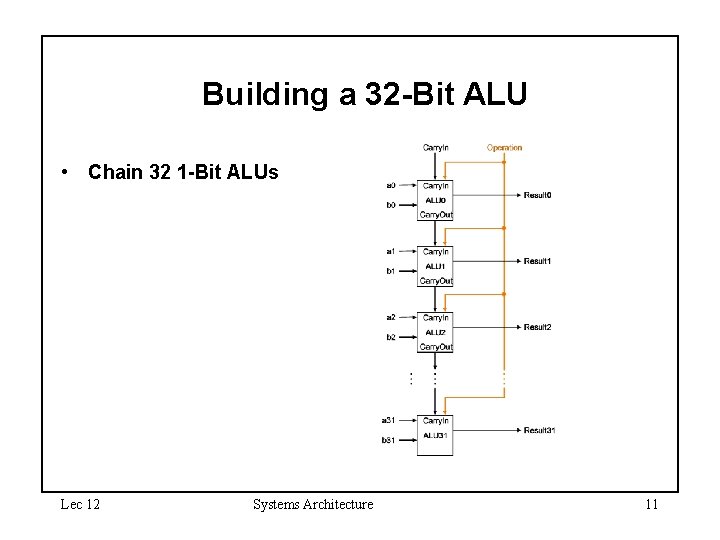
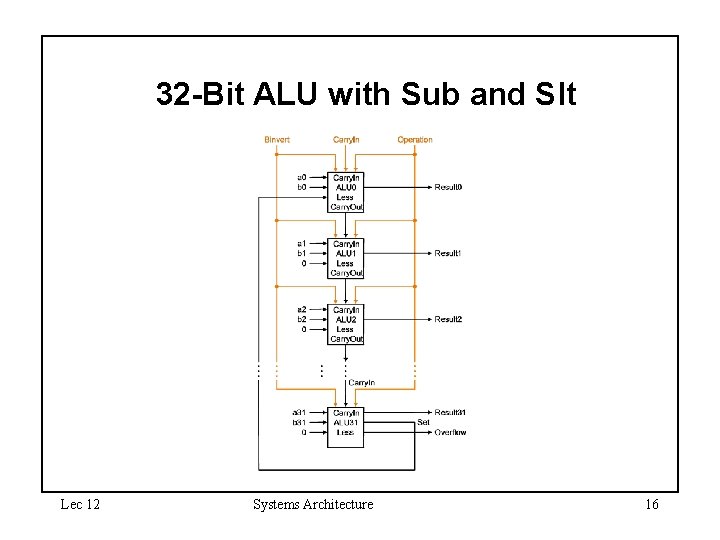
Building a 32 -Bit ALU • Chain 32 1 -Bit ALUs Lec 12 Systems Architecture 11

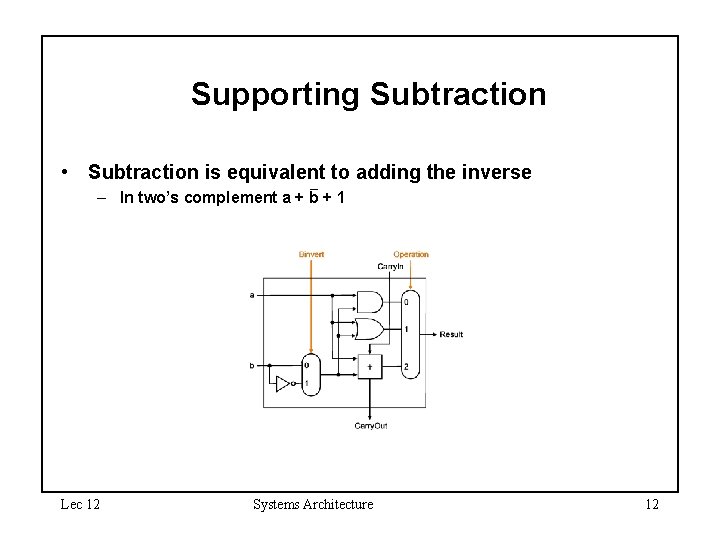
Supporting Subtraction • Subtraction is equivalent to adding the inverse – In two’s complement a + b + 1 Lec 12 Systems Architecture 12

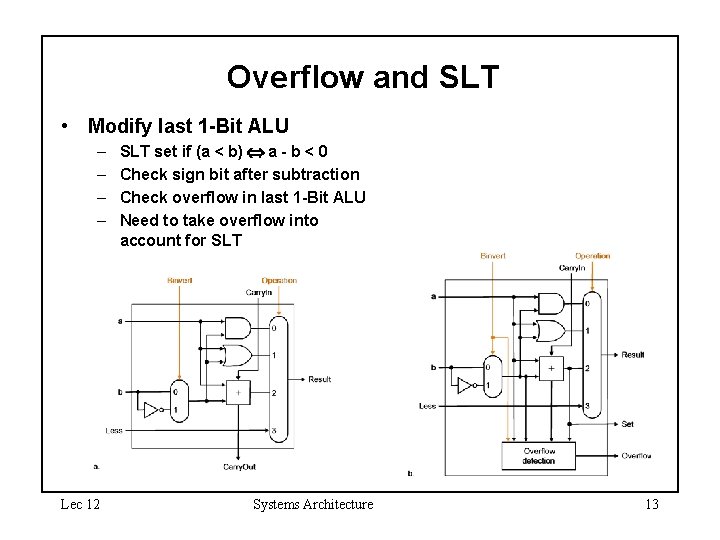
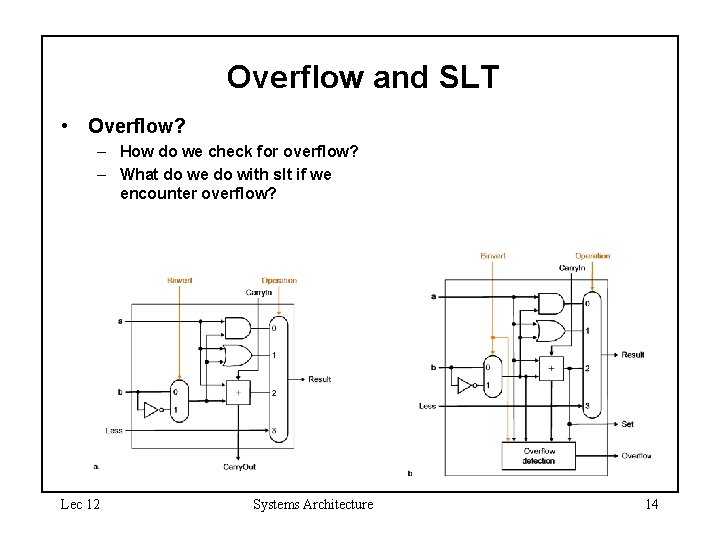
Overflow and SLT • Modify last 1 -Bit ALU – – Lec 12 SLT set if (a < b) a - b < 0 Check sign bit after subtraction Check overflow in last 1 -Bit ALU Need to take overflow into account for SLT Systems Architecture 13

Overflow and SLT • Overflow? – How do we check for overflow? – What do we do with slt if we encounter overflow? Lec 12 Systems Architecture 14

Overflow and SLT • When adding two positive numbers and a final carry out is produced, is this overflow? – Yes! This is intuitive. • When adding two negative numbers and a final carry out is produced, is this overflow? – No! Recall 2’s complement sign extend proof and the (x + -x) example. – A final carry out is expected. • Notice the carry in to the most significant (sign) bit ALU in each case and derive an overflow formula that will work in all cases. • When overflow occurs, what happens to the SLT signal? Derive this as well. Lec 12 Systems Architecture 15

32 -Bit ALU with Sub and Slt Lec 12 Systems Architecture 16

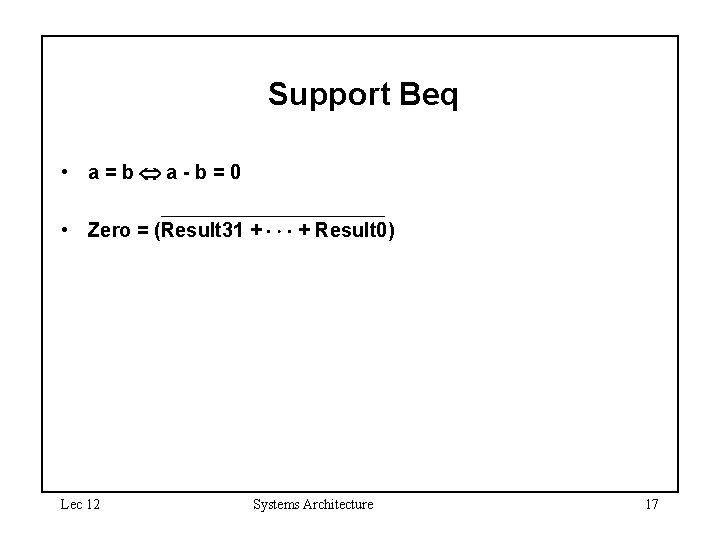
Support Beq • a=b a-b=0 • Zero = (Result 31 + + Result 0) Lec 12 Systems Architecture 17

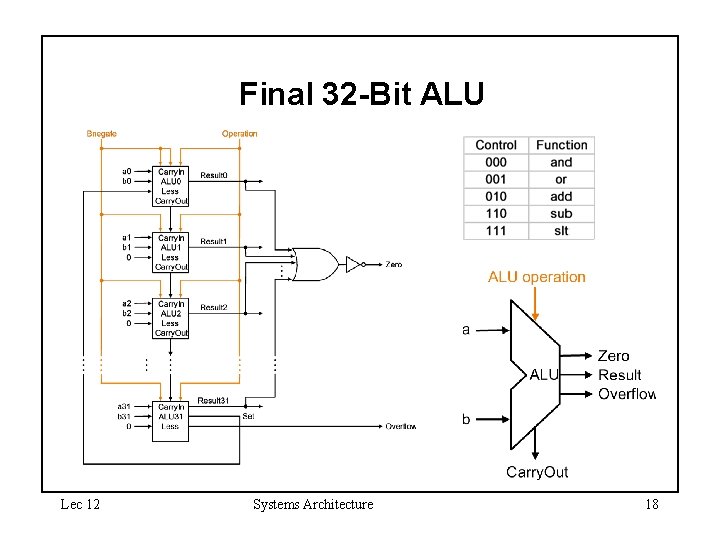
Final 32 -Bit ALU Lec 12 Systems Architecture 18

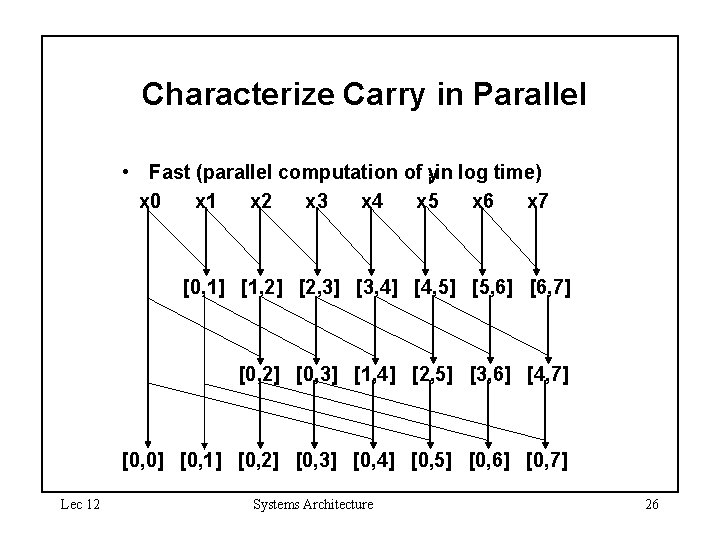
Carry Lookahead Adder • Why is it easy to add 12345 + 87654 in your head? Why is it harder to add 65345 + 89298? • If there are no carries (or if we can figure them out a priori), we can compute the additions themselves in parallel. • As it stands now, we must ripple the carries through each ALU, causing a linear time addition. This extra time is spent propagating the carry out to the next carry in. • By computing the carry in advance, we can improve addition to logarithmic time. Lec 12 Systems Architecture 19

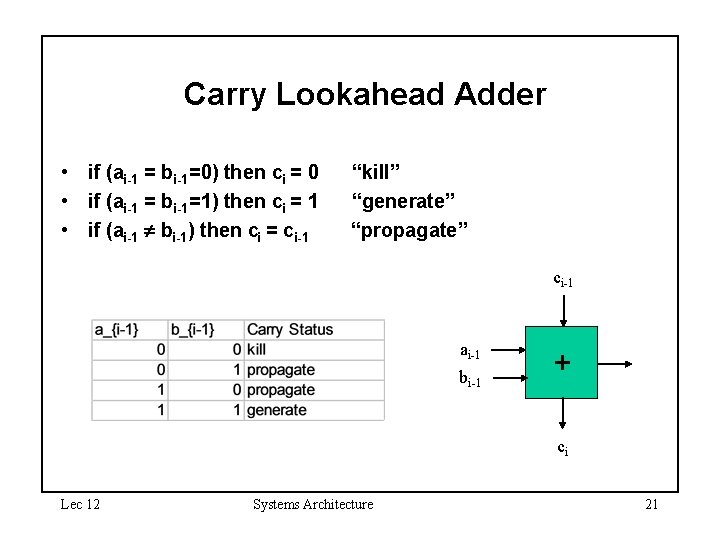
Carry Lookahead Adder • In binary addition there are only a few possible cases: – 1 + 1 (a = b = 1) – 0 + 0 (a = b = 0) – 0 + 1 or 1 + 0 (a xor b) • Notice! – The a = b = 1 case will always produce a carry out (Cout = 1), regardless of the carry in – The a = b = 0 case will never produce a carry out (Cout = 0), regardless of the carry in – The a xor b case will result in Cout = Cin • The result is the carry status (generate, kill, propagate) • Carry status signals can be combined (for example, generate followed by a kill is a kill) Lec 12 Systems Architecture 20

Carry Lookahead Adder • if (ai-1 = bi-1=0) then ci = 0 • if (ai-1 = bi-1=1) then ci = 1 • if (ai-1 bi-1) then ci = ci-1 “kill” “generate” “propagate” ci-1 ai-1 bi-1 + ci Lec 12 Systems Architecture 21

Carry Lookahead Adder • We can logically define these carry status signals as: – Generate Signal Gi = Ai AND Bi – Propagate Signal Pi = Ai XOR Bi • Now how do we compute Carry Out? Lec 12 Systems Architecture 22

Carry Lookahead Adder • Couti = G i OR (P i AND Cini) • But recall that Cini is really the previous Cout i-1, and we can compute that as Gi-1 OR (P i-1 AND Cini-1) • How did we define G and P? Can you write the recursive formula in terms of A and B only? • If so, we can compute this fast. Lec 12 Systems Architecture 23

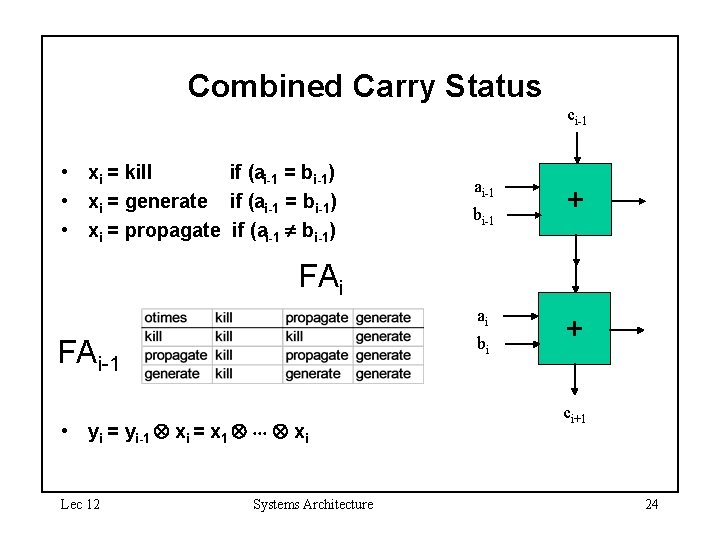
Combined Carry Status ci-1 • xi = kill if (ai-1 = bi-1) • xi = generate if (ai-1 = bi-1) • xi = propagate if (ai-1 bi-1) ai-1 bi-1 + FAi ai bi FAi-1 • yi = yi-1 xi = x 1 xi Lec 12 Systems Architecture + ci+1 24

Calculating Carry from Carry Status Lemma: – yi = kill ci = 0 – yi = generate ci = 1 – yi = propagate does not occur Proof: 1 yi = kill xi = kill ci = 0 or – xi = propagate and yi-1 = kill and ci = majority(ci-1, a i, bi) = ci-1 = kill (by induction) 2 yi = generate xi = generate ci = 1 or – xi = propagate and yi-1 = generate and ci = majority(ci-1, a i, bi) = 1 (by induction) 3 yi = propagate xi = propagate and yi-1 = propagate, which by induction leads to a contradiction Lec 12 Systems Architecture 25

Characterize Carry in Parallel • Fast (parallel computation of y i in log time) x 0 x 1 x 2 x 3 x 4 x 5 x 6 x 7 [0, 1] [1, 2] [2, 3] [3, 4] [4, 5] [5, 6] [6, 7] [0, 2] [0, 3] [1, 4] [2, 5] [3, 6] [4, 7] [0, 0] [0, 1] [0, 2] [0, 3] [0, 4] [0, 5] [0, 6] [0, 7] Lec 12 Systems Architecture 26