Systematic Listing Worksheet A The worksheet is in

Systematic Listing – Worksheet A The worksheet is in 2 sizes.

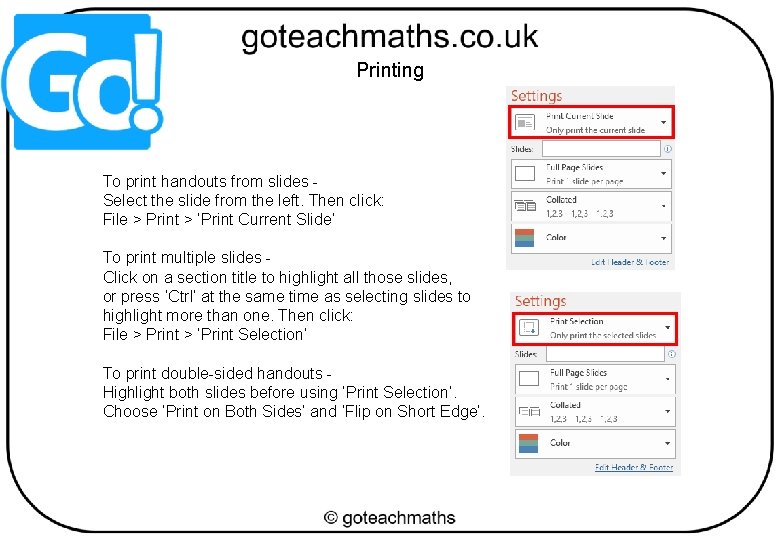
Printing To print handouts from slides Select the slide from the left. Then click: File > Print > ‘Print Current Slide’ To print multiple slides Click on a section title to highlight all those slides, or press ‘Ctrl’ at the same time as selecting slides to highlight more than one. Then click: File > Print > ‘Print Selection’ To print double-sided handouts Highlight both slides before using ‘Print Selection’. Choose ‘Print on Both Sides’ and ‘Flip on Short Edge’.

Product Rule for Counting 1 8 How many 2 -digit numbers can you make with these 2 cards? 1 8 7 1 6 5 2 7 F) How many 5 -digit numbers that are a multiple of 2 can you make? How does this change if we add a third card? 1 8 7 7 3 2 4 3 8 G) How many odd numbers greater than 50, 000 can you make? A) How many 4 -digit numbers can you make using these cards? * Sum the choices for each starting card. * How many choices do you have for the 1 st card? st * After you choose a 1 card, how many choices do you have for the 2 nd card, 3 rd card & 4 th card? 6 4 8 3 6 1 9 7 3 2 H) How many odd numbers greater than 500, 000 can you make? 2 B) How many odd 5 -digit numbers can you make with these cards? * One number must be last, how does this affect our choices? 8 7 9 1 5 2 5 1 7 4 H) How many even numbers smaller than 600, 000 can you make? 3 C) How many numbers greater than 40, 000 can you make? * How many choices are there for the 1 st card? 9 5 6 8 3 4 2 D) How many odd 6 -digit numbers can you make? * How many choices are there for the last card? 7 1 6 5 2 6 7 1 I) How many 2 -digit numbers can we make using these cards? J) How many 3 -digit numbers can we make using these cards? 2 8 1 5 6 K) How many ways can we make 3 numbers from these cards? 9 E) How many numbers greater than 300, 000 can you make? L) The number 156 is made. How many different numbers use these same digits? M) If we don’t care about their order (the number they make): how many ways can we pick 3 digits from the 5 cards?

Product Rule for Counting 2 1 8 How many 2 -digit numbers can you make with these 2 cards? 1 8 7 1 6 5 2 7 F) How many 5 -digit numbers that are a multiple of 2 can you make? How does this change if we add a third card? 1 8 7 2× 3=6 3 7 2 4 3 8 G) How many odd numbers greater than 50, 000 can you make? A) How many 4 -digit numbers can you make using these cards? * Sum the choices for each starting card. * How many choices do you have for the 1 st card? st * After you choose a 1 card, how many choices do you have for the 2 nd card, 3 rd card & 4 th card? 4 choices × 3 choices × 2 choices × 1 choice = 24 numbers 4 8 3 6 6 1 9 7 3 2 H) How many odd numbers greater than 500, 000 can you make? 2 B) How many odd 5 -digit numbers can you make with these cards? * One number must be last, how does this affect our choices? 4 × 3 × 2 × 1 choice = 24 numbers 7 9 1 5 8 2 5 1 7 4 H) How many even numbers smaller than 600, 000 can you make? 3 C) How many numbers greater than 40, 000 can you make? * How many choices are there for the 1 st card? 9 3 × 4 × 3 × 2 × 1 = 72 numbers 5 6 8 3 4 2 D) How many odd 6 -digit numbers can you make? * How many choices are there for the last card? 7 1 6 5 2 9 E) How many numbers greater than 300, 000 can you make? 4 × 5 × 4 × 3 × 2 × 1 = 480 numbers 7 1 I) How many 2 -digit numbers can we make using these cards? J) How many 3 -digit numbers can we make using these cards? 2 5 × 4 × 3 × 2 × 1 × 2 = 240 numbers 6 8 1 5 6 K) How many ways can we make 3 numbers from these cards? L) The number 156 is made. How many different numbers use these same digits? M) If we don’t care about their order (the number they make): how many ways can we pick 3 digits from the 5 cards?

Product Rule for Counting 2 1 8 How many 2 -digit numbers can you make with these 2 cards? 1 8 7 1 6 8 7 7 4 × 3 × 2 × 1 × 2 = 48 2× 3=6 3 2 F) How many 5 -digit numbers that are a multiple of 2 can you make? How does this change if we add a third card? 1 5 7 2 4 3 8 G) How many odd numbers greater than 50, 000 can you make? A) How many 4 -digit numbers can you make using these cards? * Sum the choices for each starting card. * How many choices do you have for the 1 st card? st * After you choose a 1 card, 7 first: 3 × 2 × 1 = 6 8 first: 3 × 2 × 1 × 2 = 12 6 + 12 = 18 how many choices do you have for the 2 nd card, 3 rd card & 4 th card? 4 choices × 3 choices × 2 choices × 1 choice = 24 numbers 4 8 3 6 4 × 3 × 2 × 1 choice = 24 numbers 9 1 5 1 8 3 4 2 8 2 6 5 2 5 1 7 = 240 4 2 first: 4 × 3 × 2 × 1 × 2 = 48 1 first: 4 × 3 × 2 × 1 × 3 = 72 4 first: 4 × 3 × 2 × 1 × 2 = 48 5 first: 4 × 3 × 2 × 1 × 3 = 72 9 E) How many numbers greater than 300, 000 can you make? 4 × 5 × 4 × 3 × 2 × 1 = 480 numbers 6 7 8 1 = 240 1 I) How many 2 -digit numbers can we make using these cards? J) How many 3 -digit numbers can we make using these cards? 2 5 × 4 × 3 × 2 × 1 × 2 = 240 numbers 1 2 7 first: 4 × 3 × 2 × 1 × 3 = 72 9 D) How many odd 6 -digit numbers can you make? * How many choices are there for the last card? 7 3 9 first: 4 × 3 × 2 × 1 × 3 = 72 6 first: 4 × 3 × 2 × 1 × 4 = 96 3 × 4 × 3 × 2 × 1 = 72 numbers 6 7 H) How many even numbers smaller than 600, 000 can you make? 3 C) How many numbers greater than 40, 000 can you make? * How many choices are there for the 1 st card? 5 9 H) How many odd numbers greater than 500, 000 can you make? 2 B) How many odd 5 -digit numbers can you make with these cards? * One number must be last, how does this affect our choices? 7 6 5 6 4 × 3 = 12 4 × 3 × 2 = 24 5 × 4 × 3 = 60 K) How many ways can we make 3 numbers from these cards? 3× 2× 1=6 L) The number 156 is made. How many different numbers use these same digits? M) If we don’t care about their order (the number they make): how many ways can we pick 3 digits from the 5 cards? We divide the total potential choices by duplicates. 60 ÷ 6 = 10

Product Rule for Counting 1 8 How many 2 -digit numbers can you make with these 2 cards? 1 8 7 1 6 5 2 7 F) How many 5 -digit numbers that are a multiple of 2 can you make? How does this change if we add a third card? 1 8 7 7 3 2 4 3 8 G) How many odd numbers greater than 50, 000 can you make? A) How many 4 -digit numbers can you make using these cards? * Sum the choices for each starting card. * How many choices do you have for the 1 st card? st * After you choose a 1 card, how many choices do you have for the 2 nd card, 3 rd card & 4 th card? 6 4 8 3 6 1 9 7 3 2 H) How many odd numbers greater than 500, 000 can you make? 2 B) How many odd 5 -digit numbers can you make with these cards? * One number must be last, how does this affect our choices? 8 7 9 1 5 2 5 1 7 4 H) How many even numbers smaller than 600, 000 can you make? 3 C) How many numbers greater than 40, 000 can you make? * How many choices are there for the 1 st card? 9 5 6 8 3 4 2 D) How many odd 6 -digit numbers can you make? * How many choices are there for the last card? 7 1 6 5 2 6 7 1 I) How many 2 -digit numbers can we make using these cards? J) How many 3 -digit numbers can we make using these cards? 2 8 1 5 6 K) How many ways can we make 3 numbers from these cards? 9 E) How many numbers greater than 300, 000 can you make? L) The number 156 is made. How many different numbers use these same digits? M) If we don’t care about their order (the number they make): how many ways can we pick 3 digits from the 5 cards?

Questions? Comments? Suggestions? …or have you found a mistake!? Any feedback would be appreciated . Please feel free to email: tom@goteachmaths. co. uk