System Modeling and Identification Lecture 3 Dr Ing

System Modeling and Identification Lecture 3 Dr. -Ing. Erwin Sitompul President University http: //zitompul. wordpress. com 2 0 President University Erwin Sitompul SMI 3/1

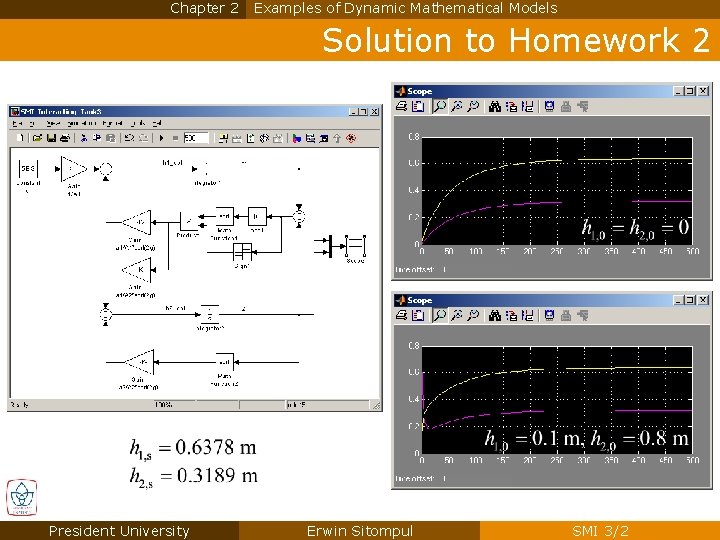
Chapter 2 Examples of Dynamic Mathematical Models Solution to Homework 2 President University Erwin Sitompul SMI 3/2

Chapter 2 General Process Models State Equations n A suitable model for a large class of continuous theoretical processes is a set of ordinary differential equations of the form: t x 1, . . . , xn u 1, . . . , um r 1, . . . , rs f 1, . . . , fn : : : Time variable State variables Manipulated variables Disturbance, nonmanipulable variables Functions President University Erwin Sitompul SMI 3/3

Chapter 2 General Process Models Output Equations n A model of process measurement can be written as a set of algebraic equations: t x 1, . . . , xn u 1, . . . , um rm 1, . . . , rmt y 1, . . . , yr g 1, . . . , gr : : : Time variable State variables Manipulated variables Disturbance, nonmanipulable variables at output Measurable output variables Functions President University Erwin Sitompul SMI 3/4

Chapter 2 General Process Models State Equations in Vector Form n If the vectors of state variables x, manipulated variables u, disturbance variables r, and vectors of functions f are defined as: n Then the set of state equations can be written compactly as: President University Erwin Sitompul SMI 3/5

Chapter 2 General Process Models Output Equations in Vector Form n If the vectors of output variables y, disturbance variables rm, and vectors of functions g are defined as: n Then the set of algebraic output equations can be written compactly as: President University Erwin Sitompul SMI 3/6

Chapter 2 General Process Models Heat Exchanger in State Space Form Tl q V ρ cp If T Tj , then State Space Equations President University Erwin Sitompul SMI 3/7 T q

Chapter 2 General Process Models Double-Pipe Heat Exchanger in State Space Form n Processes with distributed parameters are usually approximated by a series of wellmixed lumped parameter processes. n This is also the case for the heat exchanger, as shown in the next figure, which is divided into n well-mixed heat exchangers. n The space variable is divided into n equal lengths within the interval [0, L]. n After rearrangement, the mathematical model of the heat exchanger is of the form: where President University Erwin Sitompul and SMI 3/8

Chapter 2 General Process Models Double-Pipe Heat Exchanger in State Space Form n We introduce the state parameters President University Erwin Sitompul SMI 2/9

Chapter 2 General Process Models Difference Quotient n The derivation with respect to space, δT/δτ, will now be approximated by using a difference quotient. n The difference quotient itself is the equation that can be used to approximately calculate the slope of a function at a certain point. n There are three formations of difference quotient: ● Forward Difference ● Backward Difference ● Central Difference President University Erwin Sitompul SMI 2/10

Chapter 2 General Process Models Double-Pipe Heat Exchanger in State Space Form n Replacing δT/δτ with its corresponding difference will result a model that consists of a set of ordinary differential equations only. n The equation set can then be re-written in state space form. State Space Equations President University Erwin Sitompul SMI 2/11

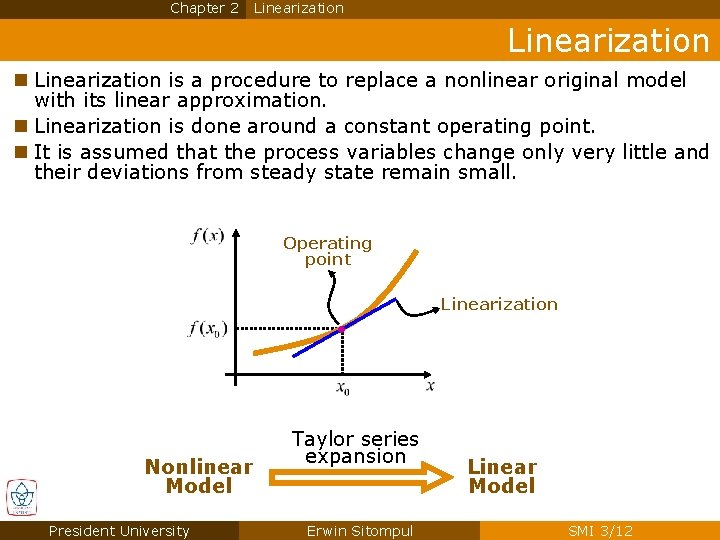
Chapter 2 Linearization n Linearization is a procedure to replace a nonlinear original model with its linear approximation. n Linearization is done around a constant operating point. n It is assumed that the process variables change only very little and their deviations from steady state remain small. Operating point Linearization Nonlinear Model President University Taylor series expansion Erwin Sitompul Linear Model SMI 3/12

Chapter 2 Linearization n The approximation model will be in the form of state space equations n An operating point x 0(t) is chosen, and the input u 0(t) is required to maintain this operating point. n In steady state, there will be no state change at the operating point, or x 0(t) = 0 President University Erwin Sitompul SMI 3/13

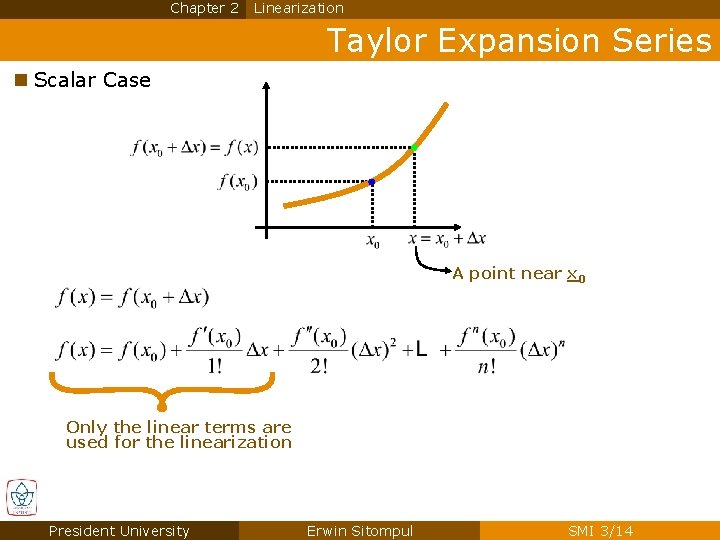
Chapter 2 Linearization Taylor Expansion Series n Scalar Case A point near x 0 Only the linear terms are used for the linearization President University Erwin Sitompul SMI 3/14

Chapter 2 Linearization Taylor Expansion Series n Vector Case where President University Erwin Sitompul SMI 3/15

Chapter 2 Linearization Taylor Expansion Series n : Number of states m : Number of inputs President University Erwin Sitompul SMI 3/16

Chapter 2 Linearization Taylor Expansion Series n Performing the same procedure for the output equations, President University Erwin Sitompul SMI 3/17

Chapter 2 Linearization Taylor Expansion Series r President University : Number of outputs Erwin Sitompul SMI 3/18

Chapter 2 Linearization Taylor Expansion Series Nonlinear Model President University Linear Model Erwin Sitompul SMI 3/19

Chapter 2 Linearization Single Tank System n The model of the system is already derived as: qi V h qo v 1 n The relationship between h and h in the above equation is nonlinear. n An operating point for the linearization is chosen, (h 0, qi, 0). President University Erwin Sitompul SMI 3/20

Chapter 2 Linearization Single Tank System n The linearization around (h 0, qi, 0) for the state equation can be calculated as: President University Erwin Sitompul SMI 3/21

Chapter 2 Linearization Single Tank System n The linearization for the ouput equation is: n Note that the input of the linearized model is now Δqi. n To obtain the actual value of state and output, the following equation must be enacted: President University Erwin Sitompul SMI 3/22

Chapter 2 Linearization Single Tank System n The Matlab-Simulink model of the linearized system is shown below. All parameters take the previous values. President University Erwin Sitompul SMI 3/23

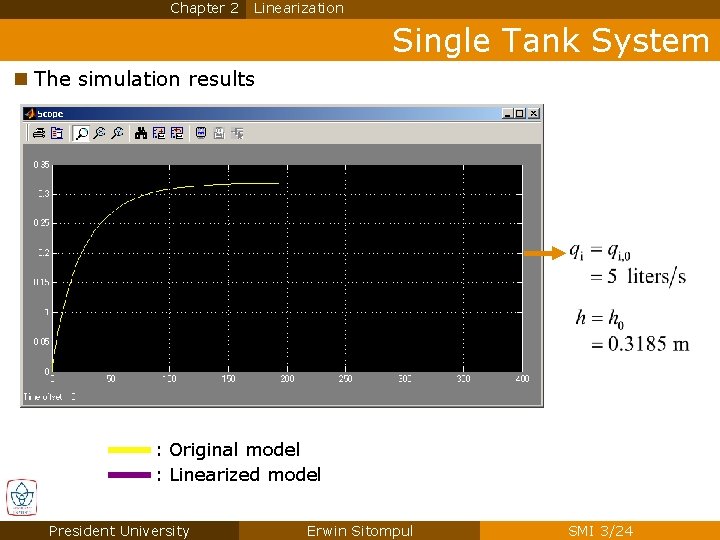
Chapter 2 Linearization Single Tank System n The simulation results : Original model : Linearized model President University Erwin Sitompul SMI 3/24

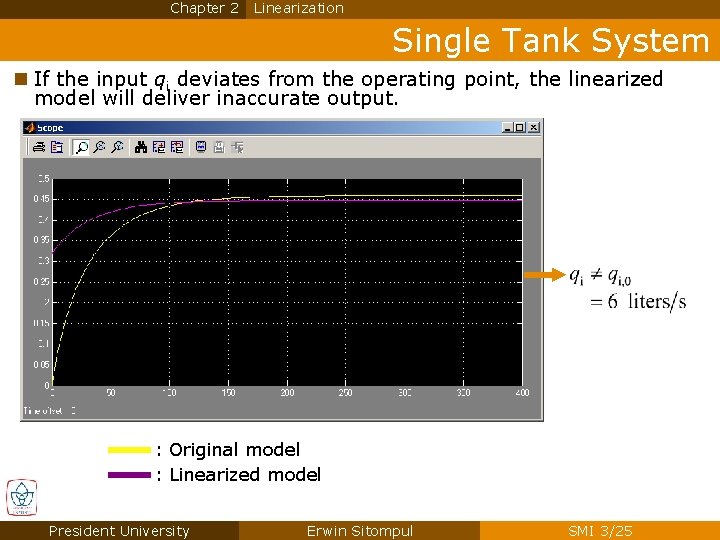
Chapter 2 Linearization Single Tank System n If the input qi deviates from the operating point, the linearized model will deliver inaccurate output. : Original model : Linearized model President University Erwin Sitompul SMI 3/25

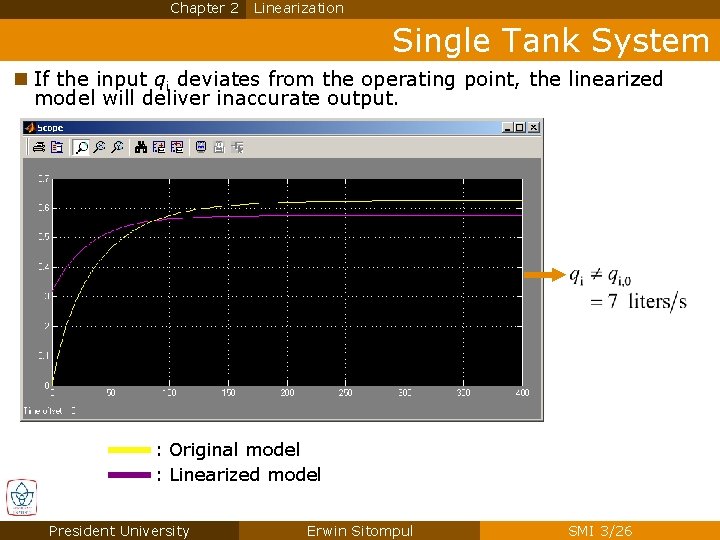
Chapter 2 Linearization Single Tank System n If the input qi deviates from the operating point, the linearized model will deliver inaccurate output. : Original model : Linearized model President University Erwin Sitompul SMI 3/26

Chapter 2 Linearization Homework 3 Linearize the interacting tank-in-series system for the operating point resulted by the parameter values as given in Homework 2. p For qi, use the last two digits of your Student ID. For example: 08 qi= 8 liters/s. p Submit the complete calculation of the linearization. p Submit also the mdl-file and the screenshots of the Matlab. Simulink file + scope. qi h 1 v 1 President University q 1 a 1 Erwin Sitompul h 2 v 2 a 2 SMI 3/27

Chapter 2 Linearization Homework 3 A Linearize the triangular-prism-shaped tank as given in Homework 2 A. p For the operating point, use qi 1 = 5 liter/s and qi 2 equals the last two digits of your Student ID divided by 10. For example: 03 qi 2= 0. 3 liter/s, 17 qi 2= 1. 7 liter/s. p Submit the complete calculation of the linearization. p Submit also the mdl-file (softcopy) and the screenshots of the Matlab-Simulink file + scope (hardcopy). qi 2 qi 1 h n Deadline: One day before the next lecture. President University a qo v Erwin Sitompul SMI 3/28 hmax