Sys MLModelica Integration Working Group Report SE DSIG

Sys. ML-Modelica Integration Working Group Report (SE DSIG meeting, Washington DC 3/24/2009) Chris Paredis Georgia Tech 1

Agenda • • Introductions Getting Organized Quick overview of initial draft document Discussion of Chapter 1 – Semantics of ports and connectors – Mock-ups for Sys. ML equivalent of spring-mass system 2

Getting Organized • Practical issues – Regular meeting slot: Wed at 10 AM Eastern – Conference call facilities? • Wiki – http: //www. omg. org/members/sysml-rtfwiki/doku. php? id=rtf 2: groups: sysml_and_modelic a_integration (requires regular OMG password) 3

WG Focus and Scope • Focus: – Reuse Modelica syntax by Integrating Modelica into Sys. ML – Integrating parts of Sys. ML into Modelica may also be worth considering, but is outside the scope of this exercise • Scope: – Cover the Modelica constructs needed for the Modelica Standard Library to be used in Sys. ML – Generate corresponding Sys. ML constructs that fit within the profiling mechanism 4

Overview of Draft Document 5

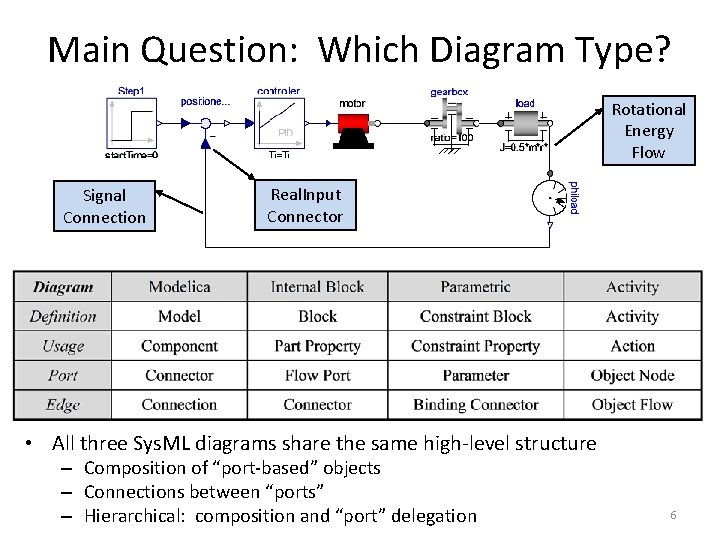
Main Question: Which Diagram Type? Rotational Energy Flow Signal Connection Real. Input Connector • All three Sys. ML diagrams share the same high-level structure – Composition of “port-based” objects – Connections between “ports” – Hierarchical: composition and “port” delegation 6

Semantics of Modelica Connectors • 2 basic types: causal and acausal • Causal: – defined as input or output • Acausal: – defined as flow or nonflow (must appear in pairs of flow and nonflow) • Basic types can be combined and nested into complex connectors 7

Semantics of Modelica Connections • Defined by “connect(. , . )” statement – no direction: “connect(a, b)” same as “connect(b, a)” • For causal connectors – Connection means Assignment – Input : = output • For acausal connectors – Connection means Kirchhoff’s Laws – Equality for nonflow: • conn. A. voltage = conn. B. voltage; conn. B. voltage = conn. C. voltage – Conservation for flow: • conn. A. current + conn. B. current + conn. C. current = 0; 8

Comments • Only “connectors” can be connected – A connector is a specialized class – The designation of connector is thus part of the definition, not of the property (usage) • In Modelica, there is no direct equivalent to Sys. ML constraint parameters – Although acausal (binding) connections exist in Modelica, they can only be used together with a corresponding flow variable to express energy flow • Modelica also differentiates based on “variability” – Constant: never changes (can be compiled in) – Parameter: value can be changed after compilation but is constant during simulation – Variable: value can change during simulation 9

Compared with ACT • ACT object nodes: – (buffered) in/outputs of tokens – tokens could be continuously streaming to reflect energy flow • Directed token-flow is not a good match Modelica semantics 10

Compared with IBD • Similar: – Flow ports are similar to Modelica Connectors – could indicate the flow of signals and/or energy • Different: – in/out/inout refers to direction of flow (sign of flow variable), not causality – in/out/inout are defined for port properties (usage) while in Modelica input/output/flow is defined in the connector definition (not usage) – Connections are typed and directed in Sys. ML while untyped and undirected in Modelica 11

Compared with PAR • Similar: – Parameters are similar to Modelica Connectors – (Binding) connections are untyped and undirected as in Modelica • Different: – Currently only acausal parameters in Sys. ML — an issue is pending to add input/output causality – A Modelica connector is a Class not a property – No notion of flow in Sys. ML — no notion of Kirchhoff’s current law in the corresponding connections 12

Mock-ups 1. Modelica IBD (Chris, Peter, Wladimir) 2. Modelica PAR (Chris) 3. Modelica IBD+PAR (Sandy) 13

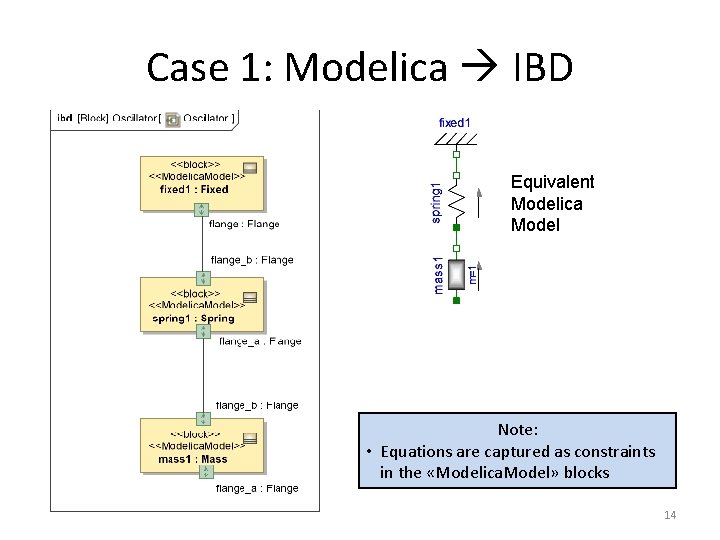
Case 1: Modelica IBD Equivalent Modelica Model Note: • Equations are captured as constraints in the «Modelica. Model» blocks 14

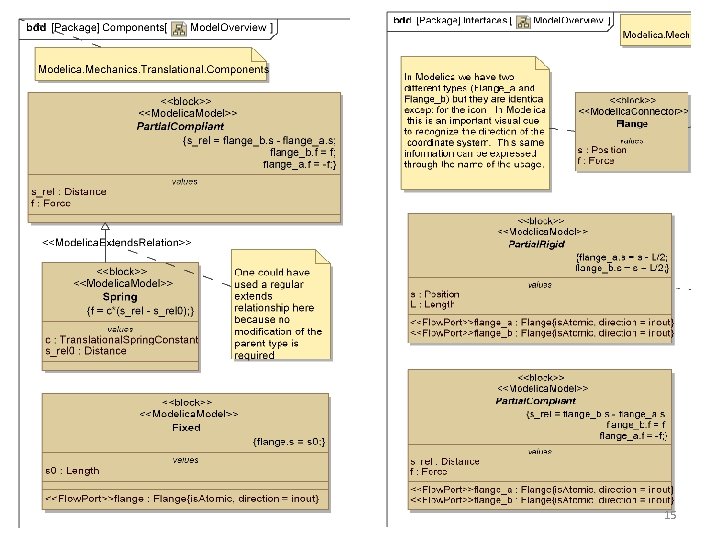
15

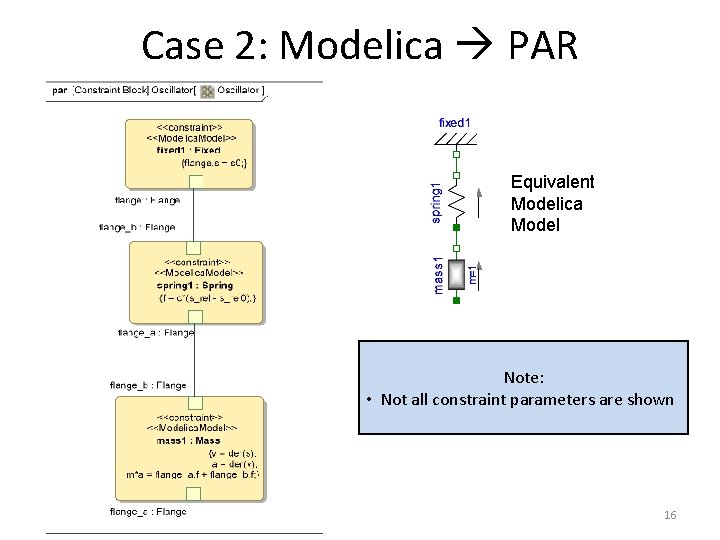
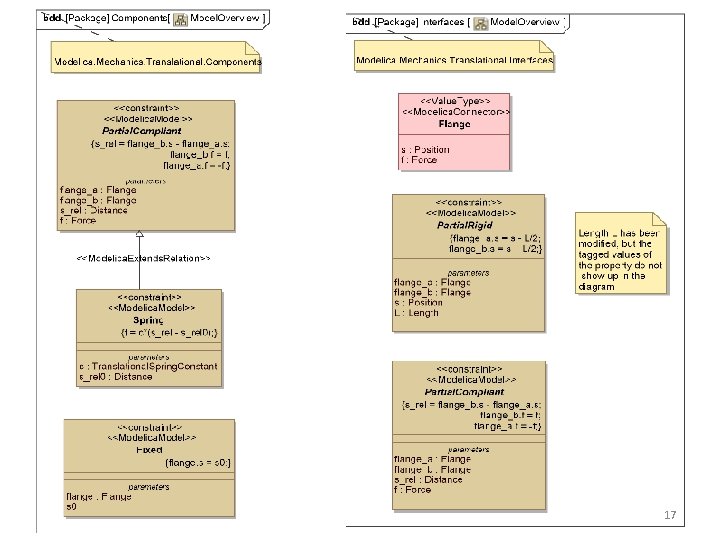
Case 2: Modelica PAR Equivalent Modelica Model Note: • Not all constraint parameters are shown 16

17

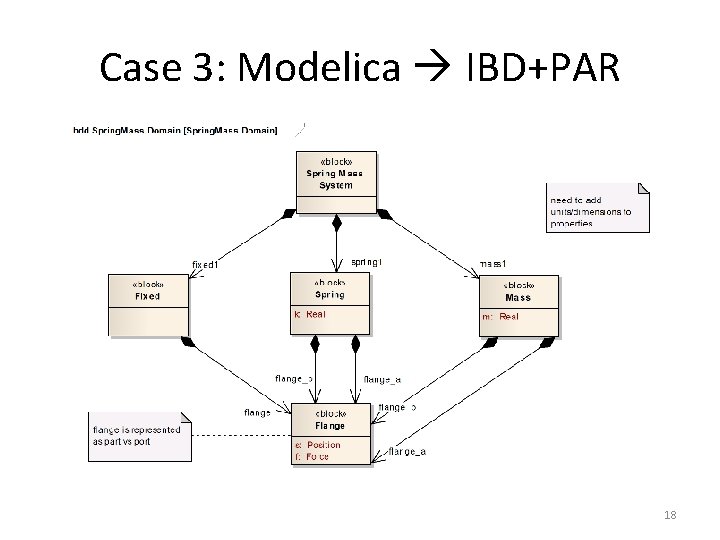
Case 3: Modelica IBD+PAR 18

Spring Mass System - IBD 19

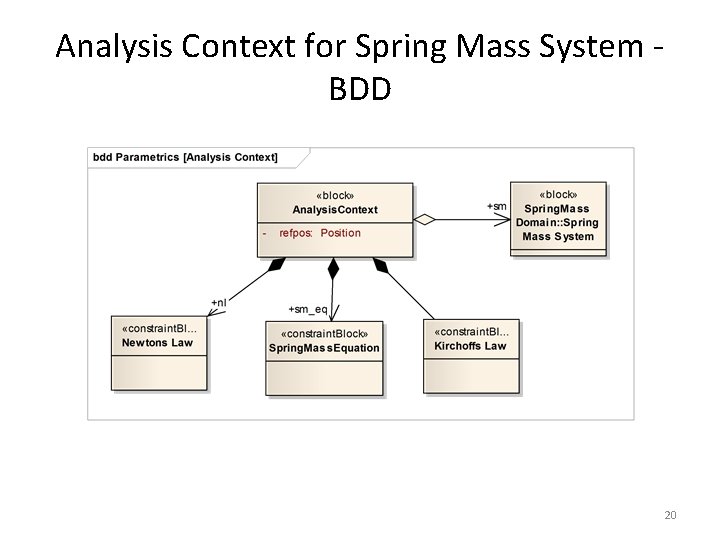
Analysis Context for Spring Mass System BDD 20

Spring Mass System - Parametrics Same structure as ibd, but added constraints and represented flange properties Much of this model would be abstracted away with Sys. ML 4 Modelica stereotypes for constraining across and through variables 21

Discussion • No perfect match - • Simplicity versus explicitness in semantics • What are the reusable models? to support reuse, we should create Sys. ML structures that match the reusable model structures 22