Sys ML and Modelica Integration Working Group Meeting

Sys. ML and Modelica Integration Working Group Meeting 3/11/09 Peter Fritzson Wladimir Schamai

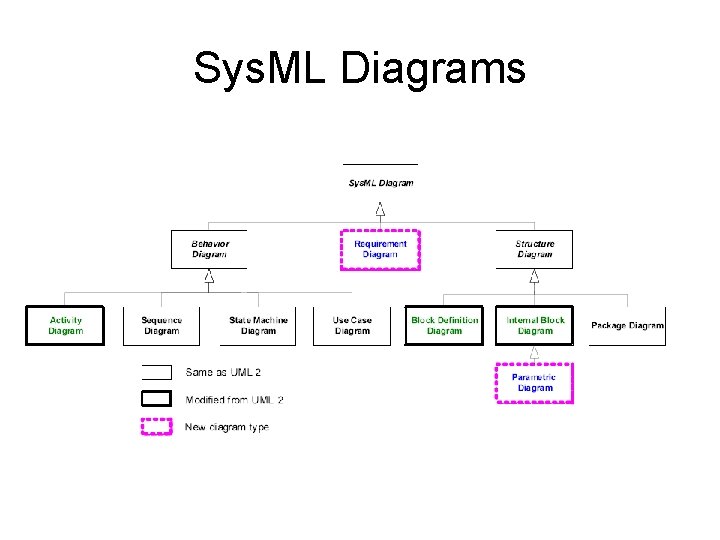
Sys. ML Diagrams

Sys. ML and Modelica Object-Oriented Paradigm • Main structural units: – Sys. ML: block (=class in object-oriented sense) – Modelica: class (=class in object-oriented sense) • Sys. ML and Modelica are dedicated to modeling of system structure and behavior • Object-oriented paradigm: Encapsulation of object data and operations – Sys. ML and Modelica models represent both: • Structure of a system – Inheritance, composition, aggregation, usages and interconnection of components (by means of ports and connections) • Behavior of a system or its component – in Sys. ML: Block operations, State Machine or Activity Diagram which invoke block operations – in Modelica: Equations, algorithm statements

(Recall) Car Suspension Example structure behavior This approach violates the encapsulation principle of the OO paradigm (it separates object structure from its behavior)

Sys. ML Structure Diagrams • Diagrams represent a view on the model data – BDD (block definition) shows • Block inheritance, composition/aggregation • A block can represent a system, sub-system, etc. – IBD (block usage) shows • Blocks usage (Part. Property), their ports and connectors – Parametric Diagram (Constraint. Block usage=instance) • Shows Constraint. Block usages (Constraint. Properties), parameters (variables) and binding connectors (pure equality) between constraint usages • A Constraint. Block does not represent a system or a sub-system, but constraints imposed on a system property (attribute) Sys. ML Constraint Blocks are inappropriate for representing Modelica Classes

Proposed Mapping Sys. ML to Modelica Structural Constructs • Block (Sys. ML) to Class (Modelica) – Difference: Terminology – Good conformity (inheritance, composition/aggregation) • Flow. Port (Sys. ML) to Connector (Modelica) – Difference: Terminology – Missing in Sys. ML: Kirchhoff laws semantics in ports definition (flow var. -> sum to zero, non-flow var. -> equality) – Modelica components usually interact through ports (=connectors) • Connector (Sys. ML) to Connection (Modelica) – Difference: Terminology – Difference: in Modelica Connections cannot be decomposed -> no Association Classes are allowed but they can be modeled explicitly – Difference: • In Modelica it is not allowed to connect components through hierarchy levels (except the inner/outer concepts) • Sys. ML connectors are 1: 1 (connect 2 ports) , Modelica connections can be n: m

Modelica Equation-Based Modeling Paradigm • Modelica equation-based modeling is new (compared to traditional object-oriented programming languages) – Class behavior is defined by • Class equations – for continuous-time behavior modeling • And/or class algorithm sections, same as procedural function and related to a method of a class in OO-languages (but without side effects) – for discrete-time behavior but also for continuous-time

Modelica Equation-Based Modeling Paradigm • Modelica algorithm statements can be represented by Sys. ML Block Operations, Activity Diagram or State Machine – Reflecting traditional OO approach with procedural operations – Such diagrams are not yet supported in Modelica and should be introduced • Sys. ML does not yet support the equation-based modeling paradigm – No means for modeling dynamic behavior of blocks using equations • Sys. ML Parametric Diagram is a structural diagram – It does not represent dynamic behavior of a system, it is intended to express constraints to structural attributes • Conclusion: New behavioral diagram is required for modeling class behavior using equations

Questions From The Last Meeting • 1) One could argue that we are using constraint parameters to “define” variables rather than just “constrain” them. For instance, mass 1 model: : L has a default value of 0 in Modelica and could thus be left unbound in the diagram. Is this a good idea? What are the alternatives? • Based on the proposed approach this will not be an issue since there will be no variables without default values. (Unbound variables still need to be solved for)

Questions From The Last Meeting • 2) Can constraint properties include “state”? According to Roger only for integrator states. Note: that this would be the case in the Modelica Model if all the Modelica parameters were bound to properties • • Based on the proposed approach this will not be an issue since Modelica classes are not mapped to Constraint. Blocks. Instead the Modelica classes are mapped to Sys. ML blocks which can contain behavior and state variables

Questions From The Last Meeting • 3) We use constraint parameters to represent “internal” variables (e. g. , the position, s, of mass 1 model) — these variables are fully constrained through the model equations (e. g. , v = der(s)), and should never be further constrained by binding them to other parameters. Is it acceptable to model these variables as constraint parameters? • Based on the proposed approach this will not be an issue since there will be no additional binding required

Questions From The Last Meeting • 4) The meaning of a binding connector in the diagram has been changed — it now reflects Kirchhoff semantics for flow variables. Is this acceptable? (it violates the strict semantics of a stereotype). What are the alternatives? • We should introduce the Kirchhoff law semantics to Sys. ML Ports and Connectors

Questions From The Last Meeting • 5) Is it meaningful to bind structural properties to time-varying variables? It seems that the value of such a property would then be ill-defined or ambiguous outside a specific analysis context. If so, would it not make sense to define it only inside the analysis context? • Based on the proposed approach this will not be an issue since there will be no additional binding required

Questions From The Last Meeting • 6) In a «Modelica. Model» we using types defined in the Modelica Standard Library. In the structural model, we may use equivalent units/dimensions but defined as different Value. Types. How do we best reconcile these differences? • We should align the types used by Modelica Standard Library and Sys. ML SI Units

Questions From The Last Meeting • 7) Translating the current «Modelica. Model» into the Modelica language would require resolving all the bindings to external properties first. This may be difficult if there are complex relationships between these properties that need to be resolved first. • Based on the proposed approach this will not be an issue since the mapping is unambiguous

Questions From The Last Meeting • 7) It is likely that certain properties in the structural model need to be bound to simulation results rather than model variables (e. g. , the settling time of the suspension can only be determined through simulation). How do we best handle this • To be discussed…

Car Suspension Example How to Reuse Modelica Standard Library Models in Own Models?

Modelica Standard Library • Pre-defined models from different engineering disciplines • Models are re-used in user defined models by means of: – Usage • Instantiation of classes – Inheritance • Interfaces (connectors) are inherited • Implementation (equations and algorithm section) is inherited • Modelica Standard Library needs to be imported into your model

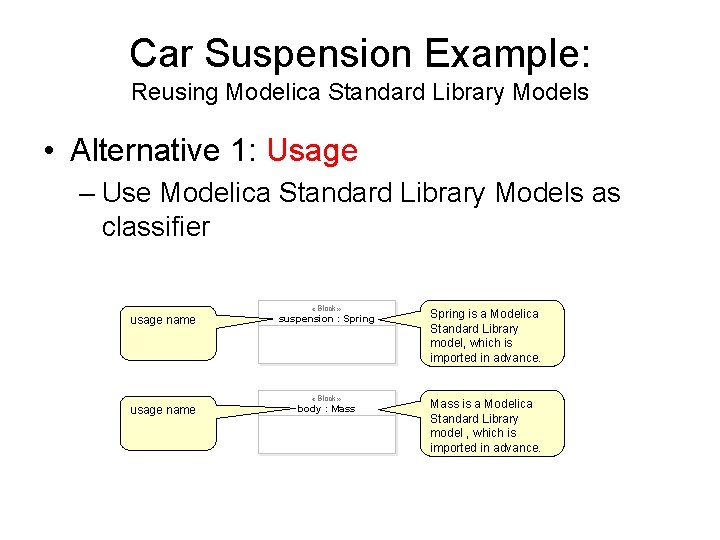
Car Suspension Example: Reusing Modelica Standard Library Models • Alternative 1: Usage – Use Modelica Standard Library Models as classifier «Block» Spring is a Modelica Standard Library model, which is imported in advance. «Block» Mass is a Modelica Standard Library model , which is imported in advance. usage name suspension : Spring usage name body : Mass

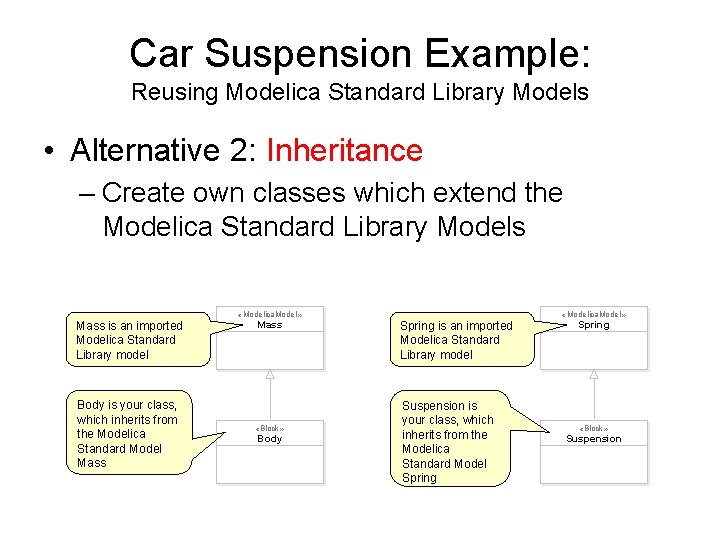
Car Suspension Example: Reusing Modelica Standard Library Models • Alternative 2: Inheritance – Create own classes which extend the Modelica Standard Library Models Mass is an imported Modelica Standard Library model Body is your class, which inherits from the Modelica Standard Model Mass «Modelica. Model» Mass «Block» Body Spring is an imported Modelica Standard Library model Suspension is your class, which inherits from the Modelica Standard Model Spring «Modelica. Model» Spring «Block» Suspension