Synthesizing Cubes to Satisfy a Given Intersection Pattern

Synthesizing Cubes to Satisfy a Given Intersection Pattern Weikang Qian

Outline �Intersection Pattern and the Problem �Motivation �Solution 2

Intersection Pattern of Cubes �Sum-of-product Boolean function: A set of cubes �Example: �Notation V( f ): number of minterms covered by f �Intersection pattern: numbers of minterms covered by the intersections of all subsets of cubes 3

Example of Intersection Pattern 3 cubes on 4 variables Intersection pattern depends on the total number of variables! 4

Reverse Problem �Given the number of variables and an intersection pattern, synthesize cubes to satisfy that pattern Example: Synthesize 3 cubes on 4 variables so that Sol. : One solution is 5

Reverse problem (cont. ) �Sometimes, these is no solution! Example: Synthesize 2 cubes on 4 variables so that Sol. : No solution! Why? c 0 1 1 1 1 No way to put the rectangle of 4 ones so the intersection has 1 minterms! 6

Outline �Intersection Pattern and the Problem �Motivation �Solution 7

Why Intersection Pattern? �Probabilistic computation �Digital circuit operating on random bit streams �Transform probabilities into probabilities 0, 1, 0, 0, 1, 1, 0, 0 P(x = 1) = 0. 4 P(y = 1) = 0. 5 1, 0, 1, 1, 0, 0, 1 �Application 0, 0, 0, 1, 0, 0, 0 P(z = 1) = 0. 2 �In test: Weighted random pattern generation �Hardware implementation of probabilistic algorithms 8

A Fundamental Synthesis Problem Independent 0. 5 Combinational Logic q 0. 5 ? 9

Output Probability: Analysis �If the number of inputs is n, then q = m/2 n �Each input combination has probability 1/2 n �If the Boolean function has m minterms, then q = m/2 n 5 minterms q = 5/8 10

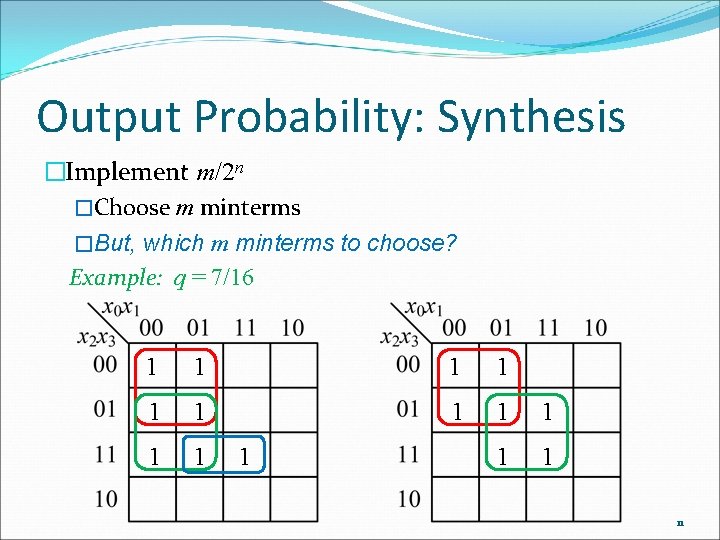
Output Probability: Synthesis �Implement m/2 n �Choose m minterms �But, which m minterms to choose? Example: q = 7/16 1 1 1 11

Two Level Logic Synthesis Problem �Given number of inputs n and m, find a SOP Boolean function with minimum cubes to cover m minterms. Optimization Flow λ = Lower bound on the number of cubes to cover m minterms Exist λ cubes to cover m interms? N λ=λ+1 Y end Related 12

Exist λ cubes to cover m miterms? �Step 1: Construct an intersection pattern so that it covers m minterms by Inclusion-Exclusion Principle: �Step 2: Synthesize cubes to satisfy the intersection pattern (Focus of this work) 13

Outline �Intersection Pattern and the Problem �Motivation �Solution 14

Preliminaries �Literals: �If cube c has k literals, then V(c) = 2 n − k �Empty cube: c = 0, V(c) = 0 �For a cube c, 15

Cube-Variable Matrix D �λ rows, each corresponding to a cube �n columns, each corresponding to a variable Example: If a row vector has k *’s, V(c) = 2 k V(c) = 2 Synthesis a cube-variable matrix to satisfy the intersection pattern 16

Properties �Negation �Column negation and column permutation of matrix maintain the intersection pattern. negate column 1 Same pattern: exchange column 1 & 2 17

Key Ideas of Solution �Determine what each column should be �Each column has 3λ candidate choices: �Only need to consider a subset of candidate choices �For example, by column negation invariability, choice equivalent to choice �Column permutation invariability: position does not matter; only number of occurrence of each candidate choice in cube-variable matrix matters 18

A Special Case �A case where all-cube intersection is non-empty �Candidate choices: those columns that do not contain both a 0 and a 1 X } Intersection Empty! �Further reduction on candidate choices: only consider columns without 0’s By column Replaced by negation invariability: 19

Special Case: Illustration with λ = 3 �Candidate choices: c 0 c 1 c 2 unknowns: y 0 y 1 y 2 y 3 y 4 y 5 y 6 y 7 �Number of occurrences in cube-variable matrix matters �Set equations between unknowns and knowns: n, V(c 0), V(c 1), V(c 0 c 1), V(c 2), V(c 0 c 2), V(c 1 c 2), V(c 0 c 1 c 2) 20

Set up Equations c 0 c 1 c 2 unknowns: y 0 y 1 y 2 y 3 y 4 y 5 y 6 y 7 knowns: n, V(c 0), V(c 1), V(c 0 c 1), V(c 2), V(c 0 c 2), V(c 1 c 2), V(c 0 c 1 c 2) Equation on n Each column belongs to one of the candidate choices y 0 + y 1 + y 2 + y 3 + y 4 + y 5 + y 6 + y 7 = n Equation on V(c 0) • If a row vector of c has k *’s, V(c) = 2 k • Relates to total number of columns with first entry * y 1 + y 3 + y 5 + y 7 = k 1 = log 2 V(c 0) Equation on V(c 1) y 2 + y 3 + y 6 + y 7 = log 2 V(c 1) Equation on V(c 2) y 4 + y 5 + y 6 + y 7 = log 2 V(c 2) 21

Set up Equations (cont. ) c 0 c 1 c 2 unknowns: y 0 y 1 y 2 y 3 y 4 y 5 y 6 y 7 knowns: n, V(c 0), V(c 1), V(c 0 c 1), V(c 2), V(c 0 c 2), V(c 1 c 2), V(c 0 c 1 c 2) c 0 c 1 c 2 Equation on V(c 0 c 1) • If a row vector of c has k *’s, V(c) = 2 k • Relates to total number of columns with 1 st and 2 nd entry both * y 3 + y 7 = k 3 = log 2 V(c 0 c 1) Equation on V(c 0 c 2) y 5 + y 7 = log 2 V(c 0 c 2) contribute to * in c 0 c 1 Equation on V(c c ) y + y = log V(c c ) 6 7 2 1 2 c 0 c 1 22

Set up Equations (cont. ) c 0 c 1 c 2 unknowns: y 0 y 1 y 2 y 3 y 4 y 5 y 6 y 7 knowns: n, V(c 0), V(c 1), V(c 0 c 1), V(c 2), V(c 0 c 2), V(c 1 c 2), V(c 0 c 1 c 2) Equation on V(c 0 c 1 c 2) • Relates to total number of columns with 1 st, 2 nd, and 3 rd entry all * y 7 = log 2 V(c 0 c 1 c 2) 23

System of Linear Equations y 0 + y 1 + y 2 + y 3 + y 4 + y 5 + y 6 + y 7 = n = k 0 y 1 + y 3 + y 5 + y 7 = log 2 V(c 0) = k 1 y 2 + y 3 + y 6 + y 7 = log 2 V(c 1) = k 2 y 3 + y 7 = log 2 V(c 0 c 1) = k 3 y 4 + y 5 + y 6 + y 7 = log 2 V(c 2) = k 4 y 5 + y 7 = log 2 V(c 0 c 2) = k 5 y 6 + y 7 = log 2 V(c 1 c 2) = k 6 y 7 = log 2 V(c 0 c 1 c 2) = k 7 Matrix form Solution 24

Solution of the Special Case �Solution �If all entries of are non-negative, then we find one set of cubes satisfying the intersection pattern �Otherwise, there is no set of cubes satisfying the intersection pattern 25

Example of Special Case Synthesize 3 cubes on 5 variables so that V(c 0) = V(c 1) = 16, V(c 0 c 1) = V(c 2) = 8, V(c 0 c 2) = V(c 1 c 2) = 4, V(c 0 c 1 c 2) = 2 Sol. : y 0 y 1 y 2 y 3 y 4 y 5 y 6 y 7 Cube-variable matrix 26

General Cases �Cases where all-cube intersection could be empty �Same ideas �Reduce candidate choices �Take numbers of occurrences as unknowns �Set up equations between unknowns and knowns �A system of linear equalities and inequalities 27

Conclusion �Problem: Synthesize a set of cubes to satisfy a given intersection pattern �Important step in the two-level logic synthesis for probabilistic computation �Solution: Determine the number of occurrences of each candidate choice �Future work: integrate into the optimization problem 28

Thank You! 29