Syntax and Semantics Form and Meaning of Programming

Syntax and Semantics Form and Meaning of Programming Languages Copyright © 2003 -2016 by Curt Hill

Definitions • Syntax: form of the expressions, statements and units • Semantics: meaning of those expressions, statements and units • What is needed for this course and beyond is a way to describe both in a clear and unambiguous way Copyright © 2003 -2016 by Curt Hill

Some Terminology • Sentence – A string of characters using some alphabet • Language – A set of sentences – Possibly infinite • Lexeme – The most basic unit of the syntax • Token – A class of lexemes Copyright © 2003 -2016 by Curt Hill

Programming Languages • Here we have characters and lexemes • A token is a class of lexemes – Any token is interchangeable with its own class for syntax – It may change the meaning, but not the form • In English: nouns, verbs etc – Nouns are interchangeable, even though the meaning changes • Reserved words, punctuation, identifiers are lexemes Copyright © 2003 -2016 by Curt Hill

Tokens and Lexemes • The lexeme is the word or item from the language itself • A token is the representation of the lexeme that is output by the scanner • Tokens are often records or objects • Tokens are often identified by an enumeration • This may be enhanced by other information, such as an identifier in a symbol table Copyright © 2003 -2016 by Curt Hill

Formal methods of describing syntax • Two men worthy of note – Noam Chomsky • Noted linguist and political activist • Devised an hierarchy of languages – John Backus • FORTRAN • Algol 60 • Backus Normal (Naur) Form Copyright © 2003 -2016 by Curt Hill

Chomsky Grammars • All languages are defined by a grammar • A grammar contains four pieces – V - an alphabet – The legal characters – T - set of terminal symbols – Terminals may appear in the language such as reserved words – Non-terminals may not appear • They are concepts or statements composed of terminals – P - a set of rewriting rules, these are called productions – Z - the distinguished symbol Copyright © 2003 -2016 by Curt Hill

More on Grammar • A language is all the legal strings accepted by this language • Terminals are those things that actually exist in the language • Non-terminals are those things that only represent syntactic items • For a parse to be complete all nonterminals must be rewritten into terminals • Lets consider a simple example Copyright © 2003 -2016 by Curt Hill

Binary • The grammar is G = {V, T, P, Z} • The alphabet, terminals and nonterminals: V = {0, 1, Z, A} • Terminals: T = {0, 1} • Non-Terminals must be Z and A • Distinguished symbol is Z • Productions are on next screen Copyright © 2003 -2016 by Curt Hill

Productions • P={ Z : : = A A : : = 1 A A : : = 0 A : : = 1 } • A production allows us to rewrite from one form to another • A non-terminal is on the left • Terminals and non-terminals on the right Copyright © 2003 -2016 by Curt Hill

Derive 101 Start with distinguished symbol Z Apply production Z: : = A A Apply production: A : : = 1 A 1 A Apply production: A : : = 0 A 10 A Apply production: A : : = 1 101 Copyright © 2003 -2016 by Curt Hill

Chomsky Hierarchy • Chomsky proposed an hierarchy of languages based on the strength of the rewriting rules • There are four – Type 0 through Type 3 • The hierarchy is based on the strength of the rewriting rules • Type 0 is strongest, 3 is weakest • In programming languages we are only interested in the 3 and 2 Copyright © 2003 -2016 by Curt Hill

Type 3 - regular languages • U : : = N or U : = WN • U and W are non-terminals and N is a terminal • A non-terminal may only be replaced by a terminal or non-terminal followed by a terminal • Often used for describing tokens • Regular expressions are of this type Copyright © 2003 -2016 by Curt Hill

Type 2 - context free languages U : : = v • • U is in set of non-terminals and v is in set of terminals and non-terminals • A terminal may be replaced by any combination of terminals and nonterminals – The context of the terminal does not matter • Most programming languages are context-free or have a few minor exceptions Copyright © 2003 -2016 by Curt Hill

Language Hierarchies Type 3 Regular Type 2 Context Free Type 1 Context Sensitive Type 0 Unrestricted Copyright © 2003 -2016 by Curt Hill

BNF • John Backus defined FORTRAN with a notation similar to Context Free languages independent of Chomsky in 1959 • Peter Naur extended it slightly in describing ALGOL • Became known as BNF for Backus Normal Form or Backus Naur Form • Meta-language is the language that describes another language Copyright © 2003 -2016 by Curt Hill

BNF Again • There are several meta-languages for BNF, the production rules given above are one • Like the Chomsky grammar there are non-terminals, productions and a start symbol – Each non-terminal represents some abstract concept in a language – There is often some notational way to distinguish a terminal from a nonterminal Copyright © 2003 -2016 by Curt Hill

Simplest notation • Form of productions: LHS RHS • Where: – LHS is a non-terminal (context free and regular grammars) – RHS is any sequence of terminals and non-terminals, including empty • There can be many productions with exactly the same LHS, these are alternatives • If the RHS contains the LHS, the rule is recursive Copyright © 2003 -2016 by Curt Hill

Simple extensions • Some times there is an alternation symbol that allows us to only need one production with the same LHS, often the vertical bar • Some times things enclosed in [ and ] are optional, they may be present zero or one times • Some times things enclosed in { and } may be present 1 or more times – Thus [{x}] allows zero or more x items Copyright © 2003 -2016 by Curt Hill

More • The extensions are often called EBNF • Syntax graphs are equivalent to EBNF • These tend to be more easy to read Copyright © 2003 -2016 by Curt Hill

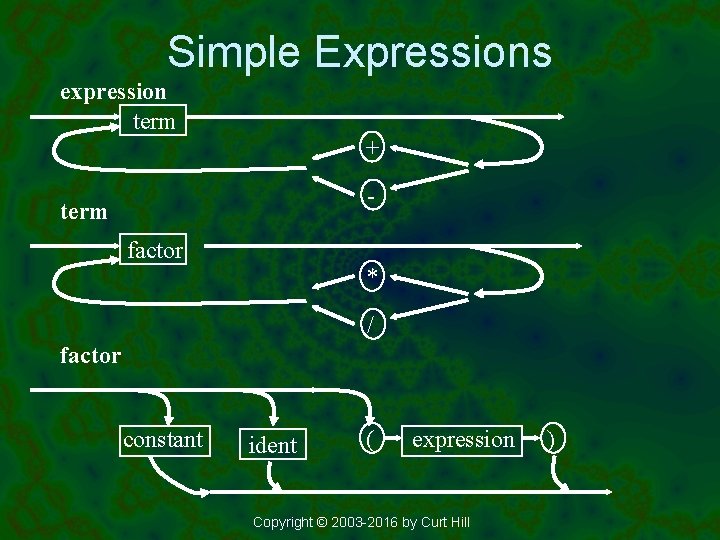
Simple Expressions expression term + - term factor * / factor constant ident ( expression Copyright © 2003 -2016 by Curt Hill )

BNF is generative • A derivation is sentence generation • Leftmost derivation – Only the leftmost non-terminal can be rewritten – This is usually the kind of derivation used by compilers – The previous derivation was leftmost • There also rightmost derivations • The order of derivation does not affect the language defined Copyright © 2003 -2016 by Curt Hill

Example BNF productions <program> <stmts> <stmt> | <stmt> ; <stmts> <stmt> <var> = <expr> <var> a | b | c | d <expr> <term> + <term> | <term> - <term> <var> | const Copyright © 2003 -2016 by Curt Hill

Example Derivation <program> => => <stmts> <stmt> <var> = <expr> a = <term> + <term> a = <var> + <term> a = b + const Copyright © 2003 -2016 by Curt Hill

Parse trees • A multi-way tree where: – Each interior node is a non-terminal – Each leaf is a terminal – The start symbol is the root – Nested under each interior node is the RHS of the production, with the LHS being the node itself • This is a handy data structure for compilers and the like Copyright © 2003 -2016 by Curt Hill

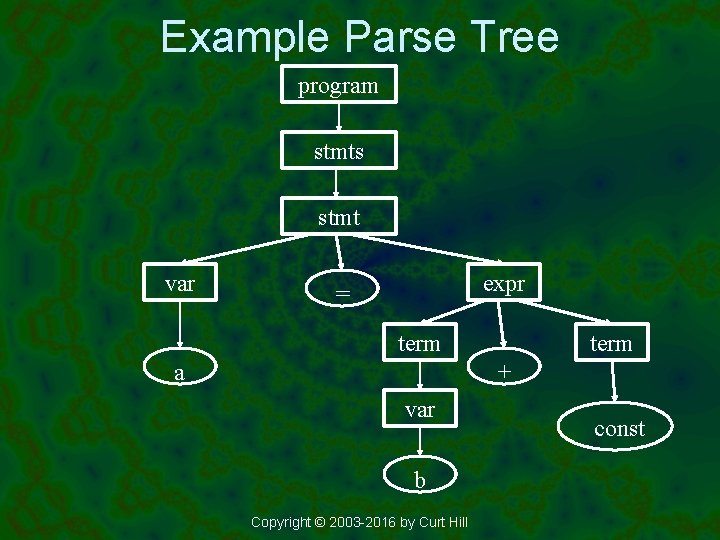
Example Parse Tree program stmts stmt var expr = term a term + var b Copyright © 2003 -2016 by Curt Hill const

Ambiguity • A grammar is ambiguous when two parse trees can be derived from the same input sequence • An ambiguous grammars usually require some fix-up in the compiler to guarantee that only one will be chosen • Many IF grammars are ambiguous concerning whether they have an else or not Copyright © 2003 -2016 by Curt Hill

BNF Problems • BNF cannot capture important information – That a variable is defined – That an expression contains proper types • Some problems like type checking could be done but would bulk out the grammar so much to be unusable – Other problems like declare before use in C++ are impossible to catch in BNF • Many of these are types of things are called Static Semantics Copyright © 2003 -2016 by Curt Hill

The Solution? • Attribute Grammars • An attempt to augment the syntax with static semantic information • Associate with each production (and with nodes of the parse tree) a function that would check the static semantic information • Check the attributes with a set of predicates Copyright © 2003 -2016 by Curt Hill

YACC Uses • YACC (Yet Another Compiler) and many other programs is a common UNIX tool for constructing compilers • YACC uses an attribute grammar of sorts – Attached to each production is a function call – You get to write the function that does the checking at that point, including code generation Copyright © 2003 -2016 by Curt Hill

Conclusion and Summary • Syntax is about the form of langauges • Semantics the meaning • BNF represents a context free grammar Copyright © 2003 -2016 by Curt Hill