Synchronous Sequential Logic Chapter 5 5 1 Introduction

Synchronous Sequential Logic Chapter 5

5 -1 Introduction n Combinational circuits n n contains no memory elements the outputs depends on the inputs Digital Circuits 2

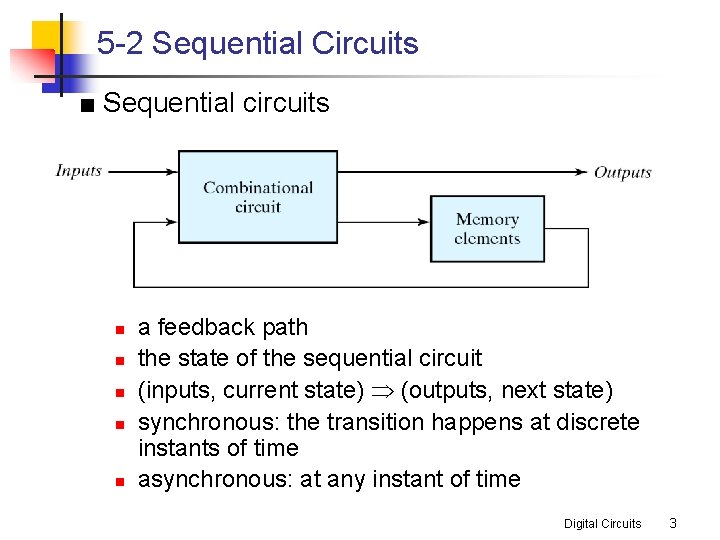
5 -2 Sequential Circuits ■ Sequential circuits n n n a feedback path the state of the sequential circuit (inputs, current state) Þ (outputs, next state) synchronous: the transition happens at discrete instants of time asynchronous: at any instant of time Digital Circuits 3

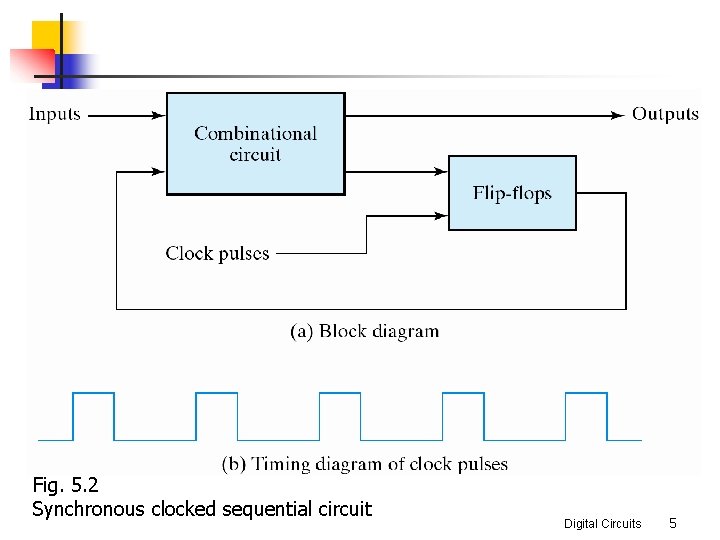
n Synchronous sequential circuits n n n a master-clock generator to generate a periodic train of clock pulses the clock pulses are distributed throughout the system clocked sequential circuits most commonly used no instability problems the memory elements: flip-flops n n n binary cells capable of storing one bit of information two outputs: one for the normal value and one for the complement value maintain a binary state indefinitely until directed by an input signal to switch states Digital Circuits 4

Fig. 5. 2 Synchronous clocked sequential circuit Digital Circuits 5

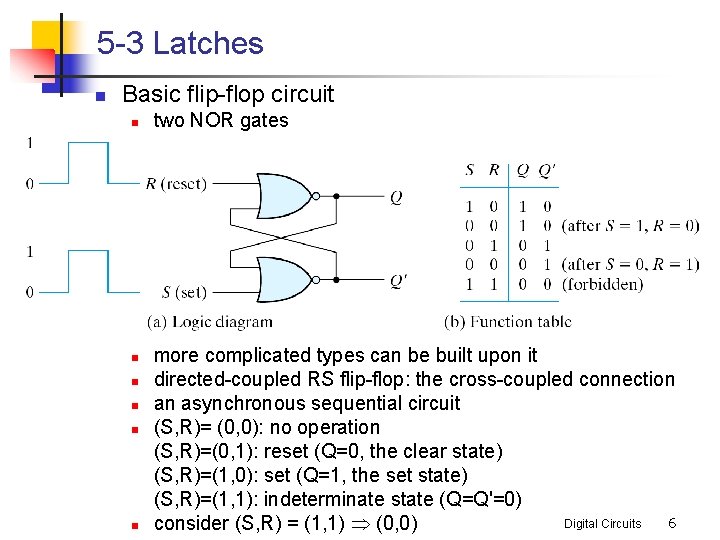
5 -3 Latches n Basic flip-flop circuit n n n n two NOR gates more complicated types can be built upon it directed-coupled RS flip-flop: the cross-coupled connection an asynchronous sequential circuit (S, R)= (0, 0): no operation (S, R)=(0, 1): reset (Q=0, the clear state) (S, R)=(1, 0): set (Q=1, the set state) (S, R)=(1, 1): indeterminate state (Q=Q'=0) 6 Digital Circuits consider (S, R) = (1, 1) Þ (0, 0)

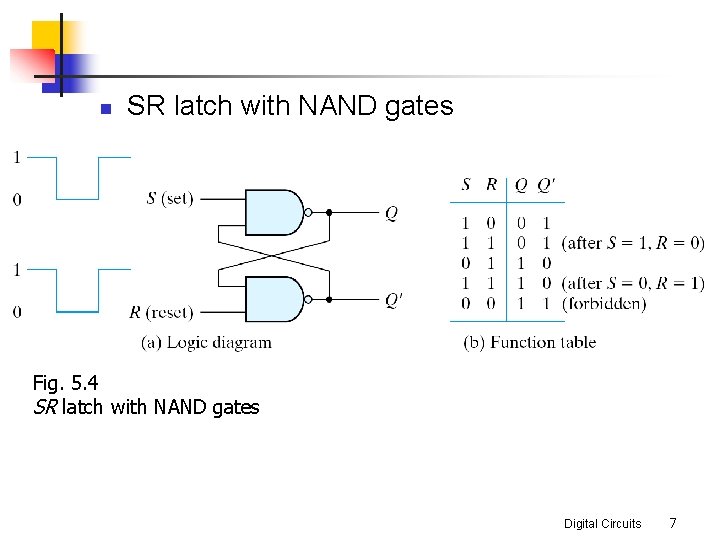
n SR latch with NAND gates Fig. 5. 4 SR latch with NAND gates Digital Circuits 7

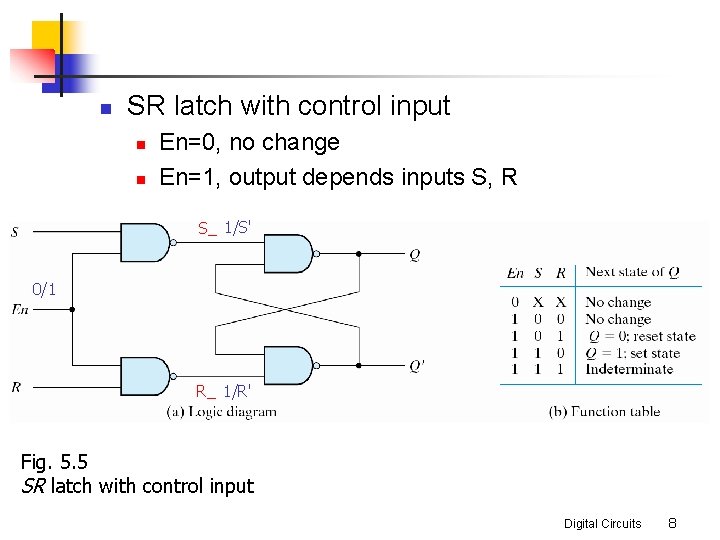
n SR latch with control input n n En=0, no change En=1, output depends inputs S, R S_ 1/S' 0/1 R_ 1/R' Fig. 5. 5 SR latch with control input Digital Circuits 8

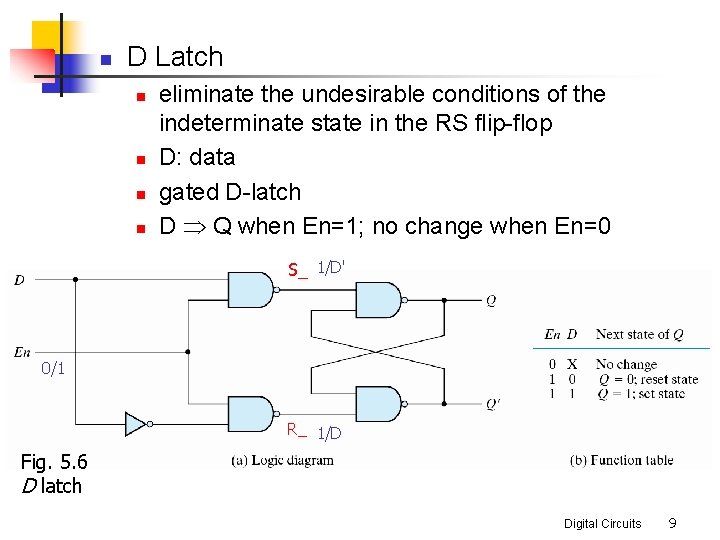
n D Latch n n eliminate the undesirable conditions of the indeterminate state in the RS flip-flop D: data gated D-latch D Þ Q when En=1; no change when En=0 S_ 1/D' 0/1 R_ 1/D Fig. 5. 6 D latch Digital Circuits 9

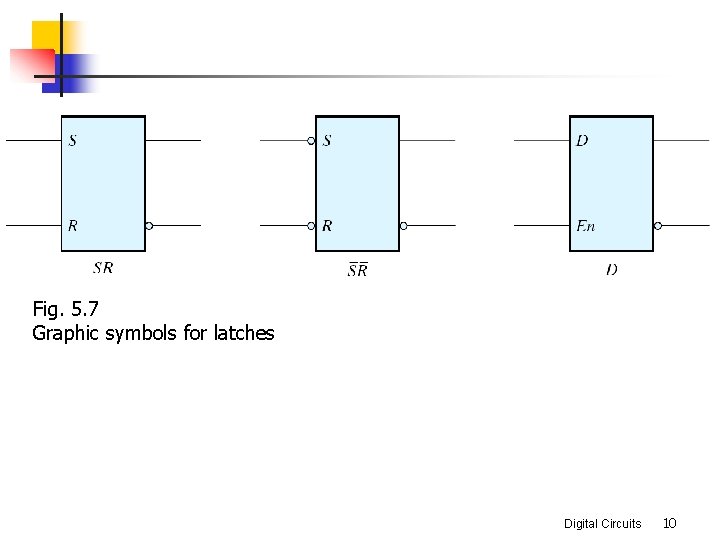
Fig. 5. 7 Graphic symbols for latches Digital Circuits 10

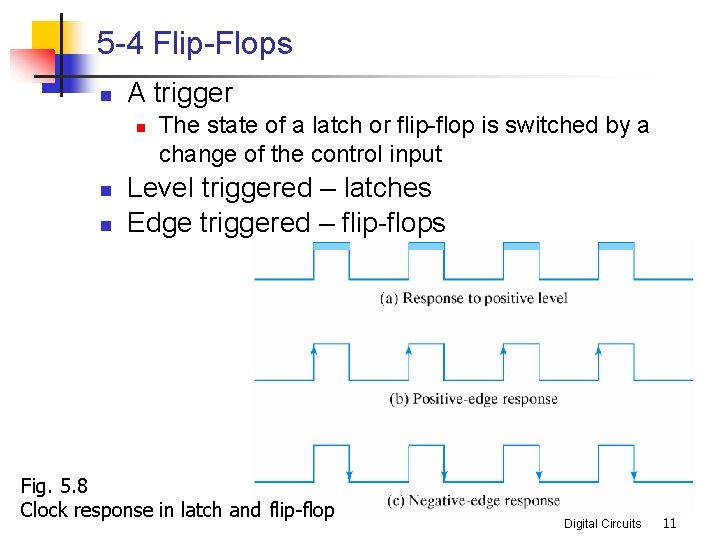
5 -4 Flip-Flops n A trigger n n n The state of a latch or flip-flop is switched by a change of the control input Level triggered – latches Edge triggered – flip-flops Fig. 5. 8 Clock response in latch and flip-flop Digital Circuits 11

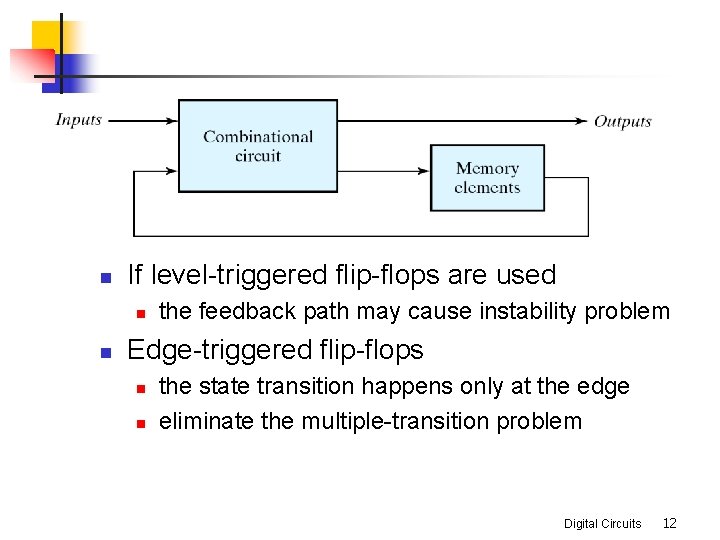
n If level-triggered flip-flops are used n n the feedback path may cause instability problem Edge-triggered flip-flops n n the state transition happens only at the edge eliminate the multiple-transition problem Digital Circuits 12

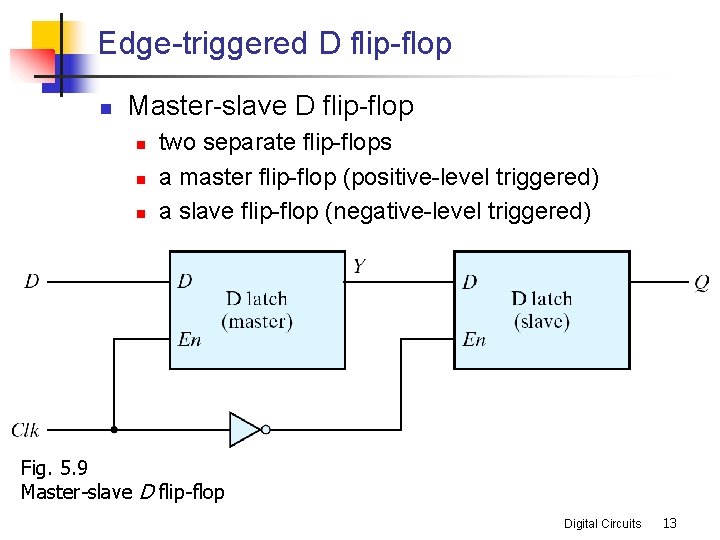
Edge-triggered D flip-flop n Master-slave D flip-flop n n n two separate flip-flops a master flip-flop (positive-level triggered) a slave flip-flop (negative-level triggered) Fig. 5. 9 Master-slave D flip-flop Digital Circuits 13

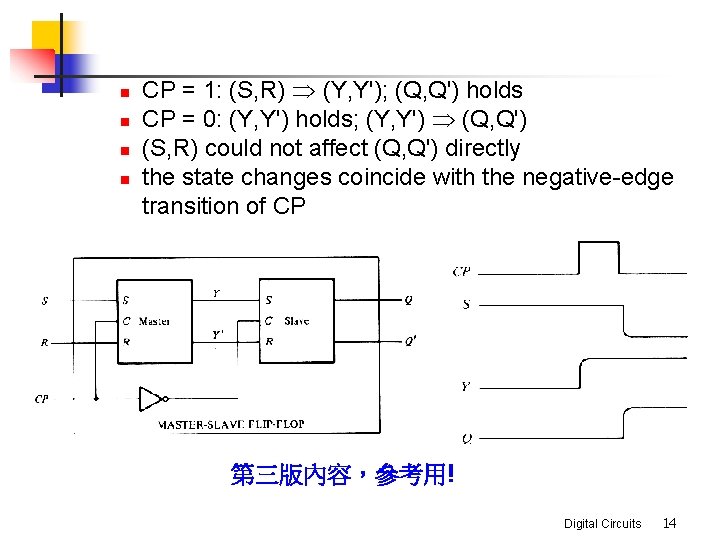
n n CP = 1: (S, R) Þ (Y, Y'); (Q, Q') holds CP = 0: (Y, Y') holds; (Y, Y') Þ (Q, Q') (S, R) could not affect (Q, Q') directly the state changes coincide with the negative-edge transition of CP 第三版內容，參考用! Digital Circuits 14

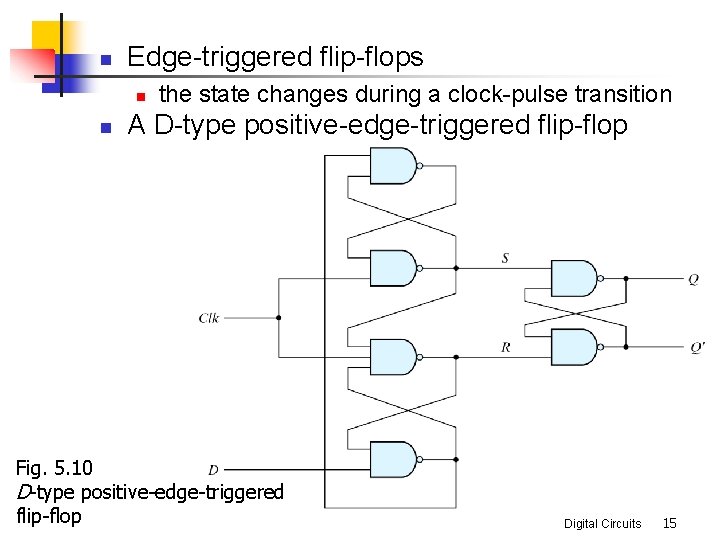
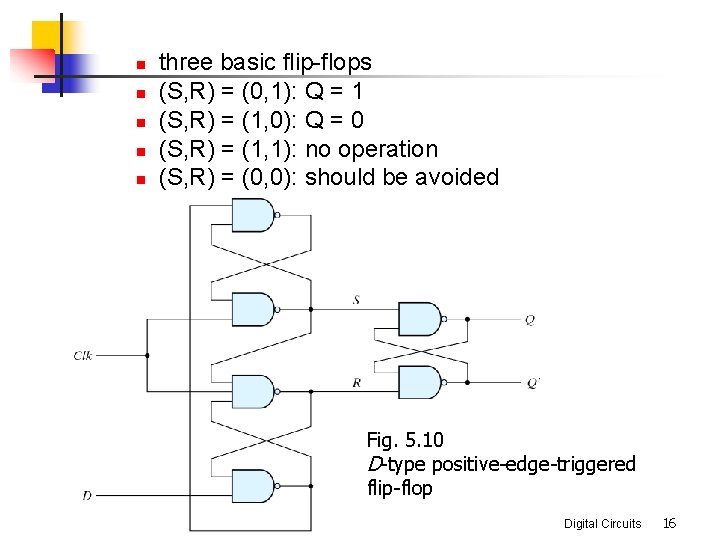
n Edge-triggered flip-flops n n the state changes during a clock-pulse transition A D-type positive-edge-triggered flip-flop Fig. 5. 10 D-type positive-edge-triggered flip-flop Digital Circuits 15

n n n three basic flip-flops (S, R) = (0, 1): Q = 1 (S, R) = (1, 0): Q = 0 (S, R) = (1, 1): no operation (S, R) = (0, 0): should be avoided Fig. 5. 10 D-type positive-edge-triggered flip-flop Digital Circuits 16

第三版內容， 參考用! Digital Circuits 17

n The setup time n n The hold time n n D input must not changes after the application of the positive CP pulse The propagation delay time n 50% VH D input must be maintained at a constant value prior to the application of the positive CP pulse The interval between the trigger edge and the stabilization of the output to a new state 50% VH Digital Circuits 18

n Summary n n n CP=0: (S, R) = (1, 1), no state change CP= : state change once CP=1: state holds Digital Circuits 19

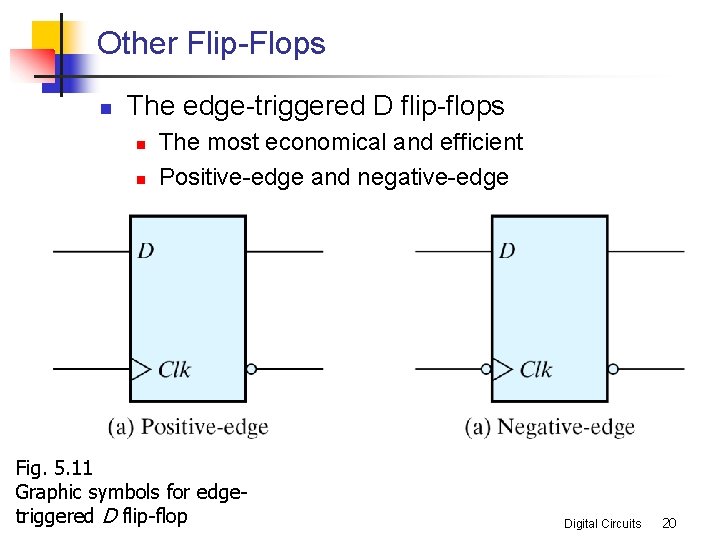
Other Flip-Flops n The edge-triggered D flip-flops n n The most economical and efficient Positive-edge and negative-edge Fig. 5. 11 Graphic symbols for edgetriggered D flip-flop Digital Circuits 20

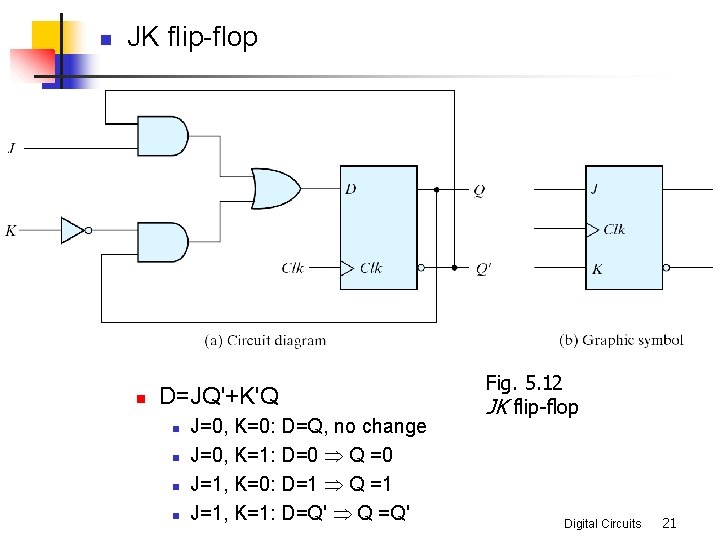
n JK flip-flop n D=JQ'+K'Q n n J=0, K=0: D=Q, no change J=0, K=1: D=0 Þ Q =0 J=1, K=0: D=1 Þ Q =1 J=1, K=1: D=Q' Þ Q =Q' Fig. 5. 12 JK flip-flop Digital Circuits 21

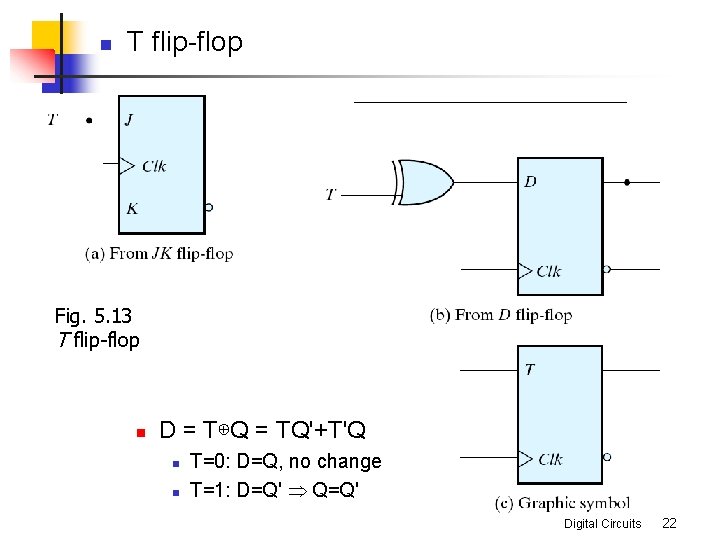
n T flip-flop Fig. 5. 13 T flip-flop n D = T⊕Q = TQ'+T'Q n n T=0: D=Q, no change T=1: D=Q' Þ Q=Q' Digital Circuits 22

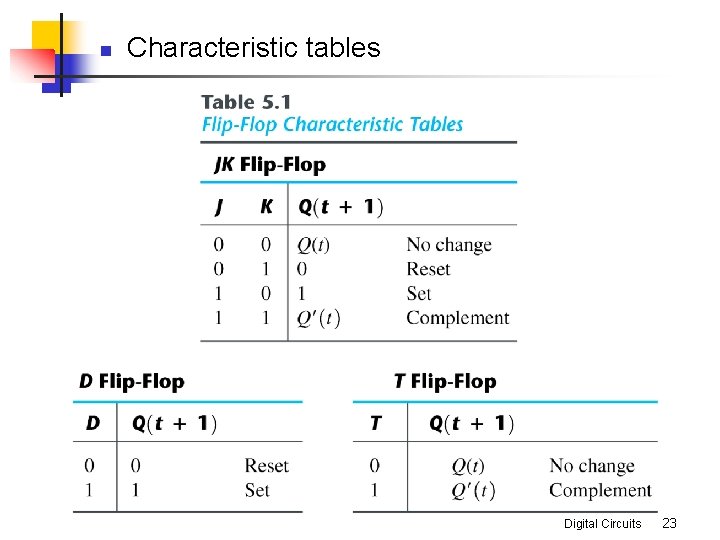
n Characteristic tables Digital Circuits 23

n Characteristic equations n D flip-flop n n JK flip-flop n n Q(t+1) = D Q(t+1) = JQ'+K'Q T flop-flop n Q(t+1) = T⊕Q Digital Circuits 24

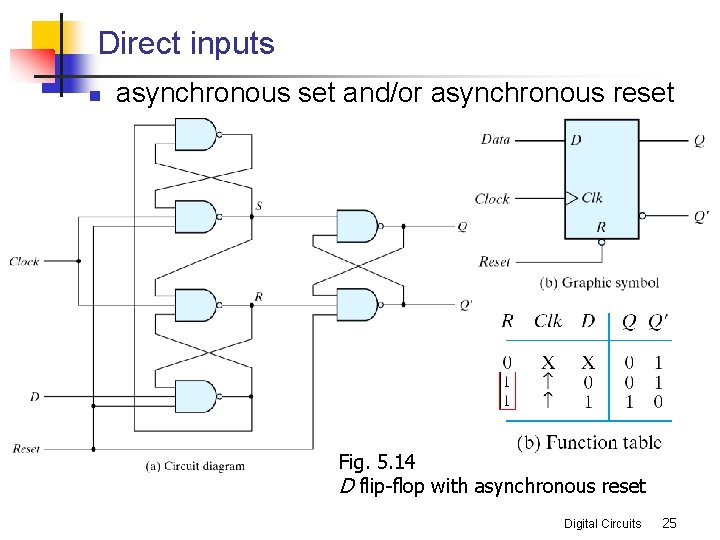
Direct inputs n asynchronous set and/or asynchronous reset Fig. 5. 14 D flip-flop with asynchronous reset Digital Circuits 25

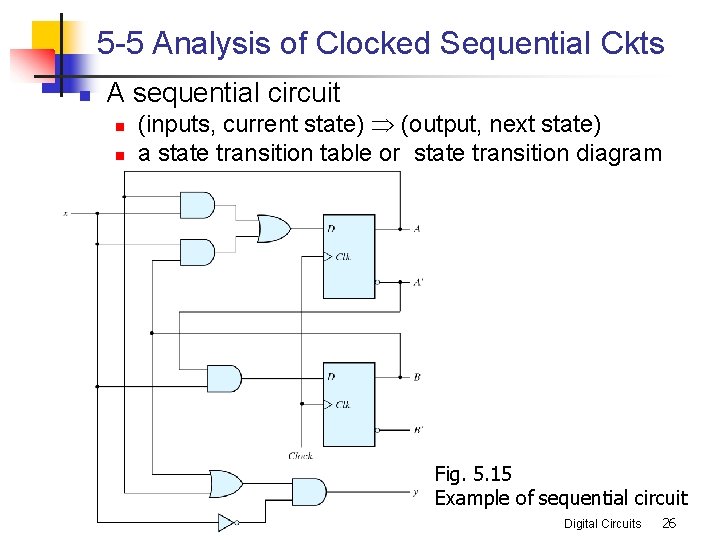
5 -5 Analysis of Clocked Sequential Ckts n A sequential circuit n n (inputs, current state) Þ (output, next state) a state transition table or state transition diagram Fig. 5. 15 Example of sequential circuit Digital Circuits 26

State equations n n n A compact form n n n A(t+1) = A(t)x(t) + B(t)x(t) B(t+1) = A'(t)x(t) A(t+1) = Ax + Bx B(t+1) = Ax The output equation n n y(t) = (A(t)+B(t))x'(t) y = (A+B)x' Digital Circuits 27

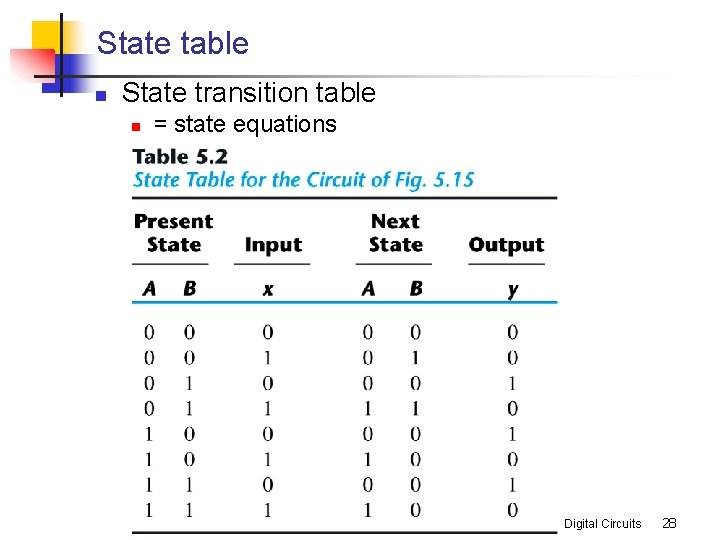
State table n State transition table n = state equations Digital Circuits 28

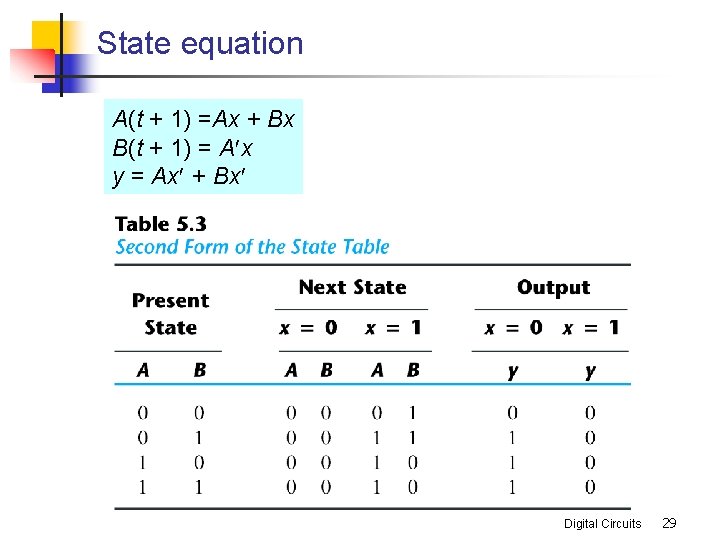
State equation A(t + 1) =Ax + Bx B(t + 1) = A x y = Ax + Bx Digital Circuits 29

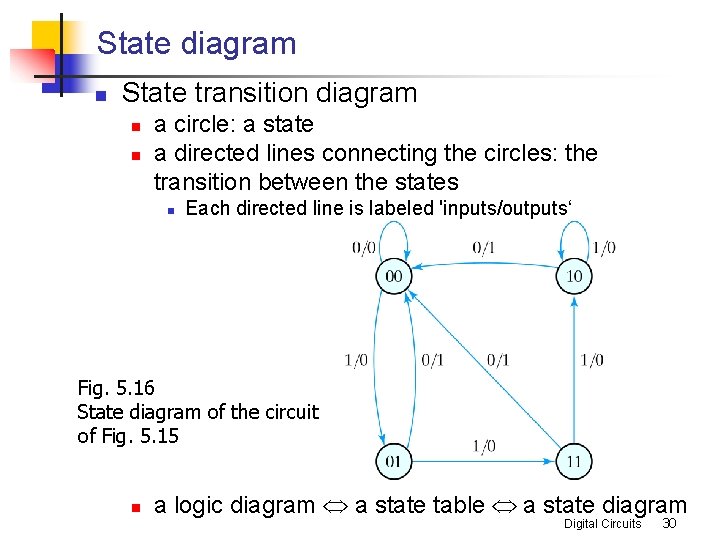
State diagram n State transition diagram n n a circle: a state a directed lines connecting the circles: the transition between the states n Each directed line is labeled 'inputs/outputs‘ Fig. 5. 16 State diagram of the circuit of Fig. 5. 15 n a logic diagram Û a state table Û a state diagram Digital Circuits 30

Flip-flop input equations n The part of circuit that generates the inputs to flip-flops n n Also called excitation functions DA = Ax +Bx DB = A'x The output equations n n to fully describe the sequential circuit y = (A+B)x' Digital Circuits 31

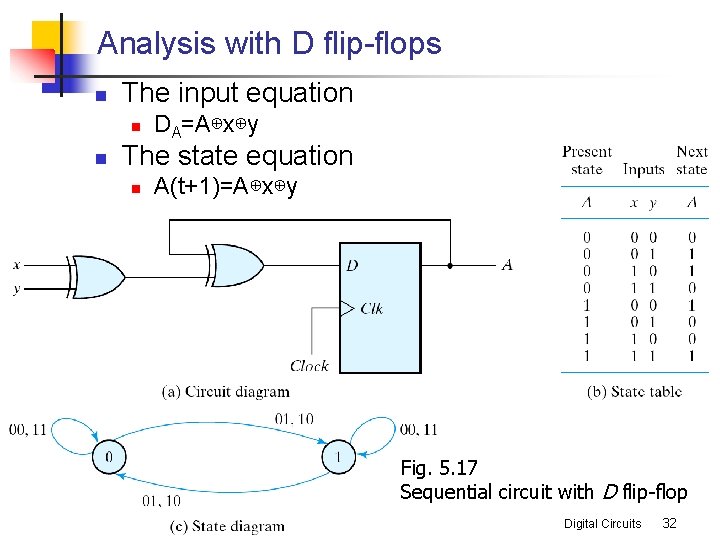
Analysis with D flip-flops n The input equation n n DA=A⊕x⊕y The state equation n A(t+1)=A⊕x⊕y Fig. 5. 17 Sequential circuit with D flip-flop Digital Circuits 32

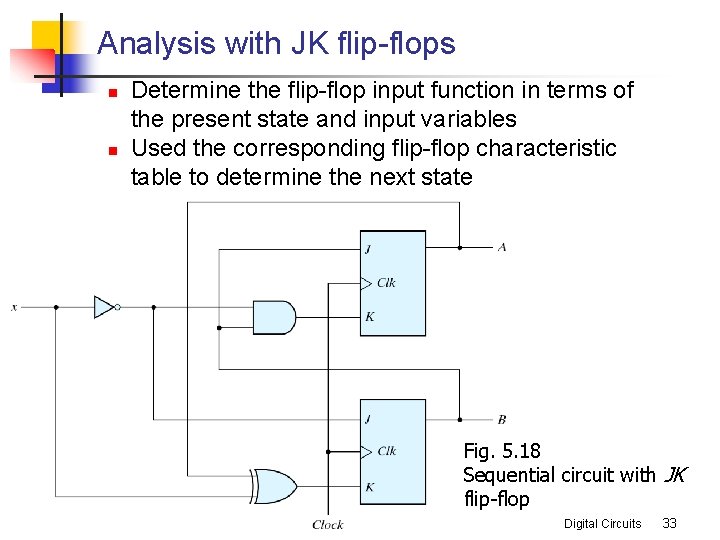
Analysis with JK flip-flops n n Determine the flip-flop input function in terms of the present state and input variables Used the corresponding flip-flop characteristic table to determine the next state Fig. 5. 18 Sequential circuit with JK flip-flop Digital Circuits 33

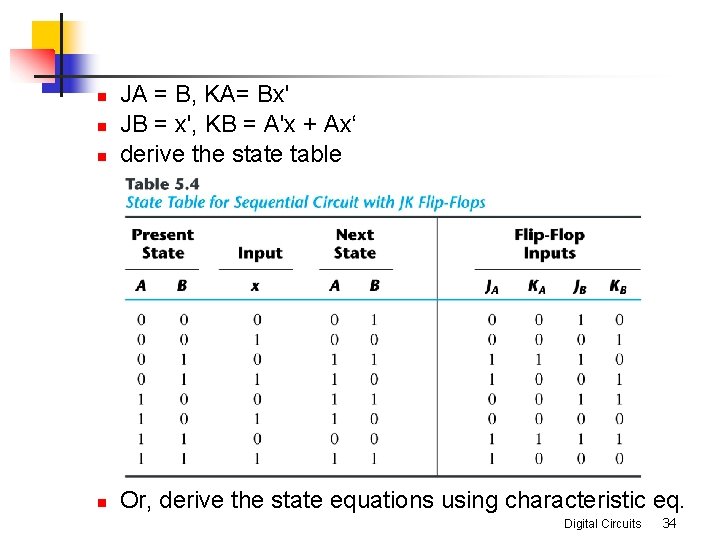
n JA = B, KA= Bx' JB = x', KB = A'x + Ax‘ derive the state table n Or, derive the state equations using characteristic eq. n n Digital Circuits 34

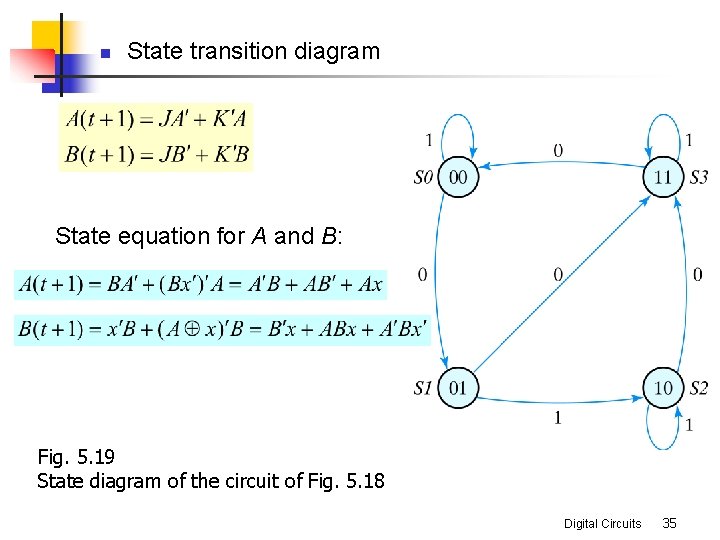
n State transition diagram State equation for A and B: Fig. 5. 19 State diagram of the circuit of Fig. 5. 18 Digital Circuits 35

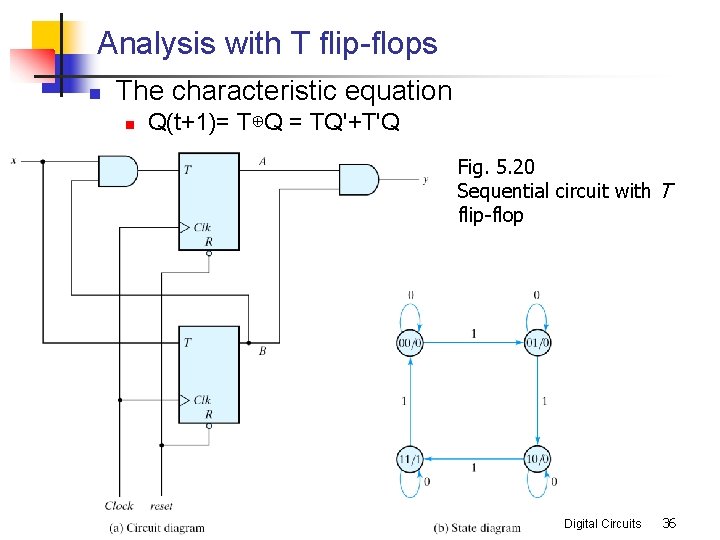
Analysis with T flip-flops n The characteristic equation n Q(t+1)= T⊕Q = TQ'+T'Q Fig. 5. 20 Sequential circuit with T flip-flop Digital Circuits 36

n The input and output functions n n TA=Bx TB= x y = AB The state equations n n A(t+1) = (Bx)'A+(Bx)A' =AB'+Ax'+A'Bx B(t+1) = x⊕B Digital Circuits 37

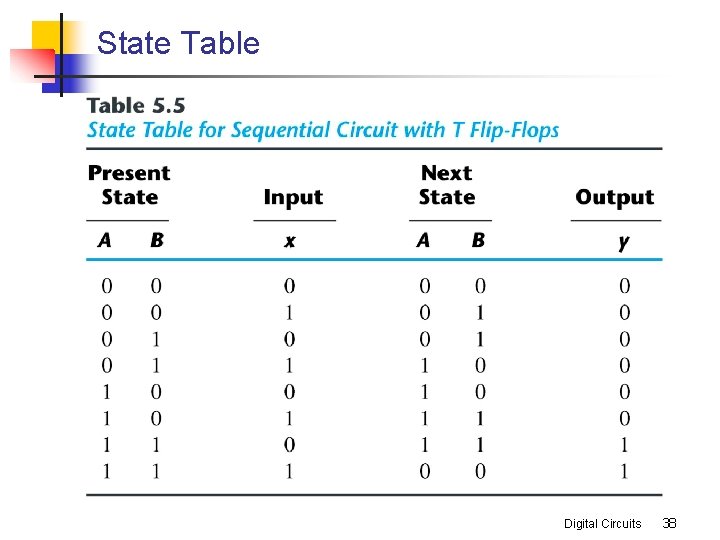
State Table Digital Circuits 38

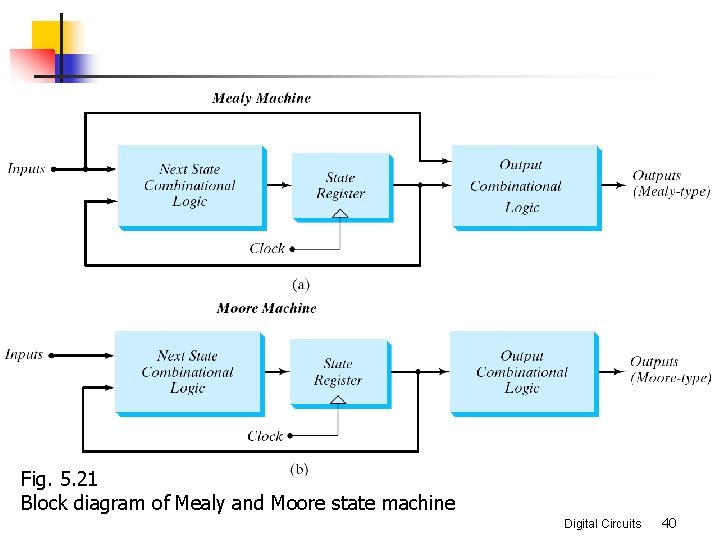
Mealy and Moore models n the Mealy model: the outputs are functions of both the present state and inputs (Fig. 5 -15) n the outputs may change if the inputs change during the clock pulse period n n the outputs may have momentary false values unless the inputs are synchronized with the clocks The Moore model: the outputs are functions of the present state only (Fig. 5 -20) n The outputs are synchronous with the clocks Digital Circuits 39

Fig. 5. 21 Block diagram of Mealy and Moore state machine Digital Circuits 40

5 -7 Synthesizable HDL Models of Sequential Circuits n Behavioral Modeling Example: Two ways to provide free-running clock Example: Another way to describe free-running clock Digital Circuits 41

Behavioral Modeling always statement Examples: Two procedural blocking assignments: Two nonblocking assignments: Digital Circuits 42

Flip-Flops and Latches ■ HDL Example 5. 1 Digital Circuits 43

Flip-Flops and Latches ■ HDL Example 5. 2 Digital Circuits 44

Characteristic Equation Q(t + 1) = Q ⊕ T Q(t + 1) = JQ + K Q For a T flip-flop For a JK flip-flop ■ HDL Example 5. 3 Digital Circuits 45

HDL Example 5 -3 (Continued) Digital Circuits 46

HDL Example 5 -4 Functional description of JK flip-flop Digital Circuits 47

State Diagram ■ HDL Example 5. 5: Mealy HDL model Digital Circuits 48

HDL Example 5 -5 (Continued) Digital Circuits 49

HDL Example 5 -5 (Continued) Digital Circuits 50

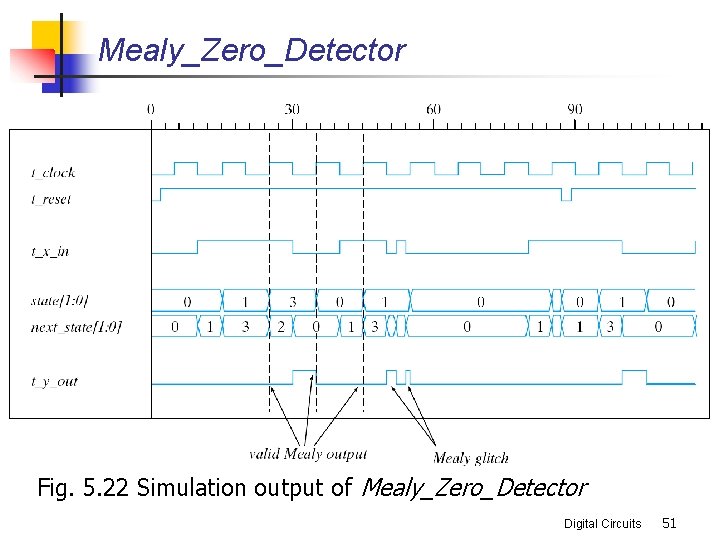
Mealy_Zero_Detector Fig. 5. 22 Simulation output of Mealy_Zero_Detector Digital Circuits 51

HDL Example 5 -6: Moore Model FSM Digital Circuits 52

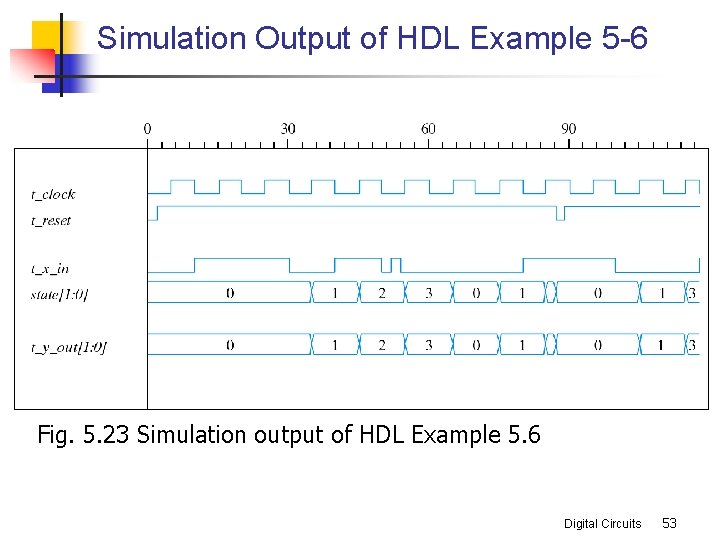
Simulation Output of HDL Example 5 -6 Fig. 5. 23 Simulation output of HDL Example 5. 6 Digital Circuits 53

Structural Description of Clocked Sequential Circuits ■ HDL Example 5. 7: State-diagram-based model Digital Circuits 54

HDL Example 5 -7 (Continued) Digital Circuits 55

HDL Example 5 -7 (Continued) Digital Circuits 56

HDL Example 5 -7 (Continued) Digital Circuits 57

HDL Example 5 -7 (Continued) Digital Circuits 58

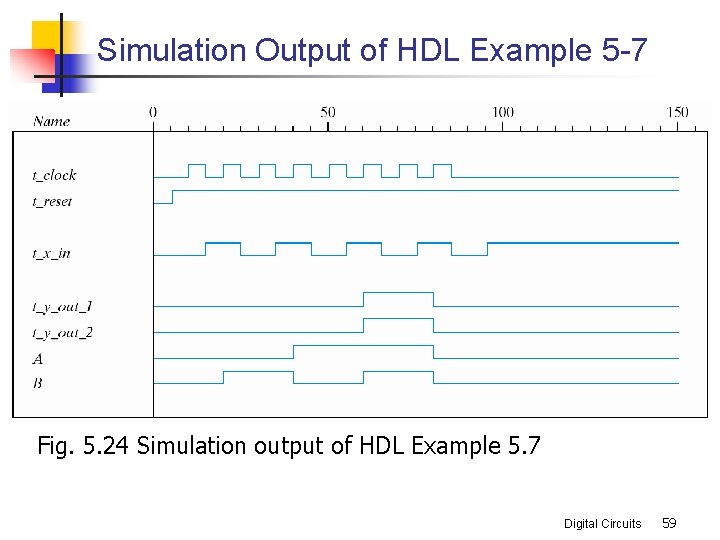
Simulation Output of HDL Example 5 -7 Fig. 5. 24 Simulation output of HDL Example 5. 7 Digital Circuits 59

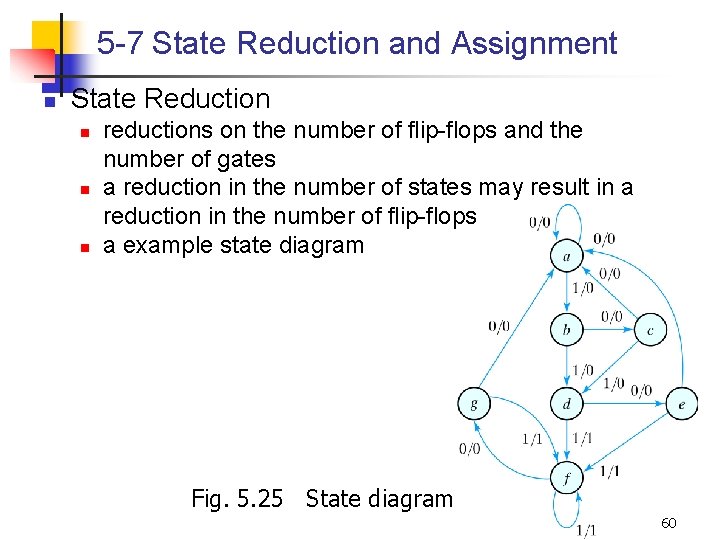
5 -7 State Reduction and Assignment n State Reduction n reductions on the number of flip-flops and the number of gates a reduction in the number of states may result in a reduction in the number of flip-flops a example state diagram Fig. 5. 25 State diagram Digital Circuits 60

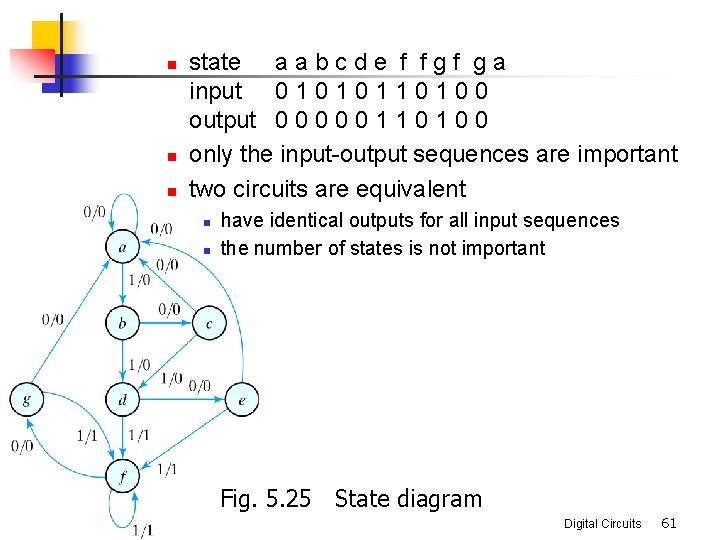
n n n state a a b c d e f f g a input 0 1 0 1 1 0 0 output 0 0 0 1 1 0 0 only the input-output sequences are important two circuits are equivalent n n have identical outputs for all input sequences the number of states is not important Fig. 5. 25 State diagram Digital Circuits 61

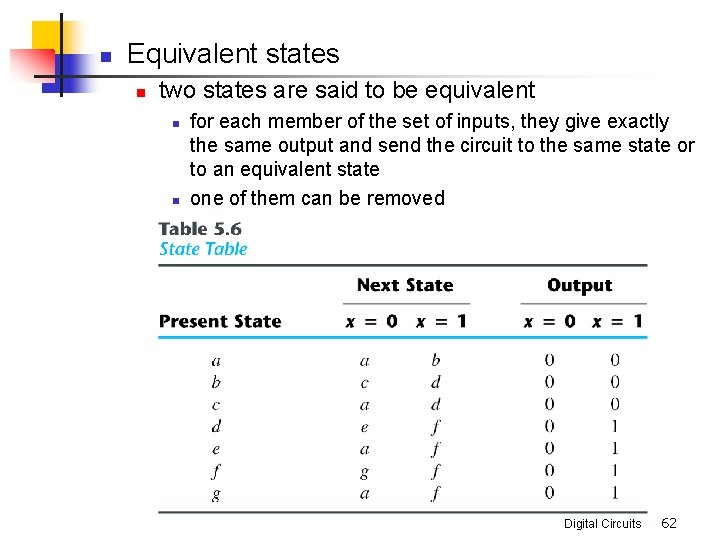
n Equivalent states n two states are said to be equivalent n n for each member of the set of inputs, they give exactly the same output and send the circuit to the same state or to an equivalent state one of them can be removed Digital Circuits 62

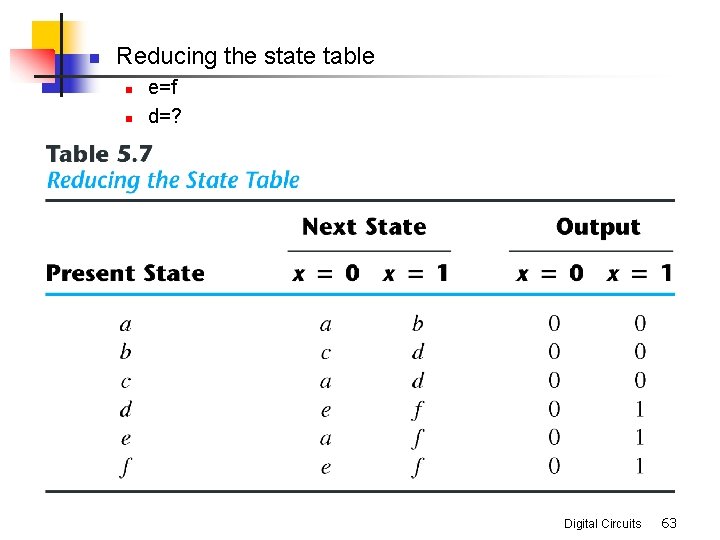
n Reducing the state table n n e=f d=? Digital Circuits 63

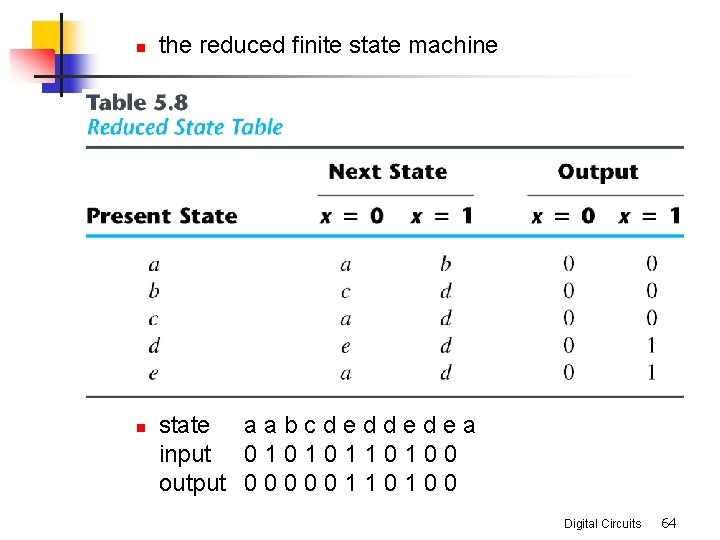
n n the reduced finite state machine state a a b c d e d e a input 0 1 0 1 1 0 0 output 0 0 0 1 1 0 0 Digital Circuits 64

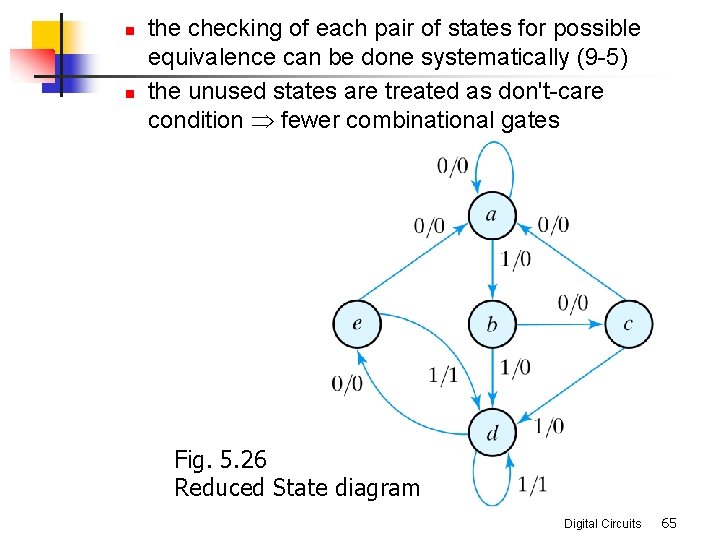
n n the checking of each pair of states for possible equivalence can be done systematically (9 -5) the unused states are treated as don't-care condition Þ fewer combinational gates Fig. 5. 26 Reduced State diagram Digital Circuits 65

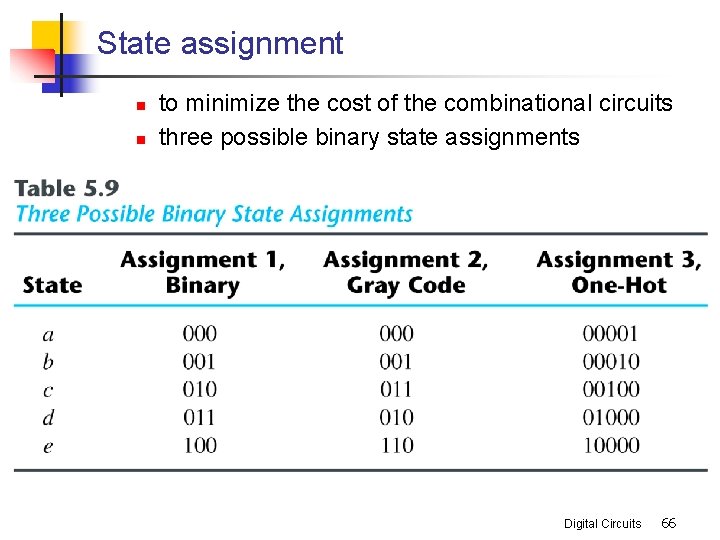
State assignment n n to minimize the cost of the combinational circuits three possible binary state assignments Digital Circuits 66

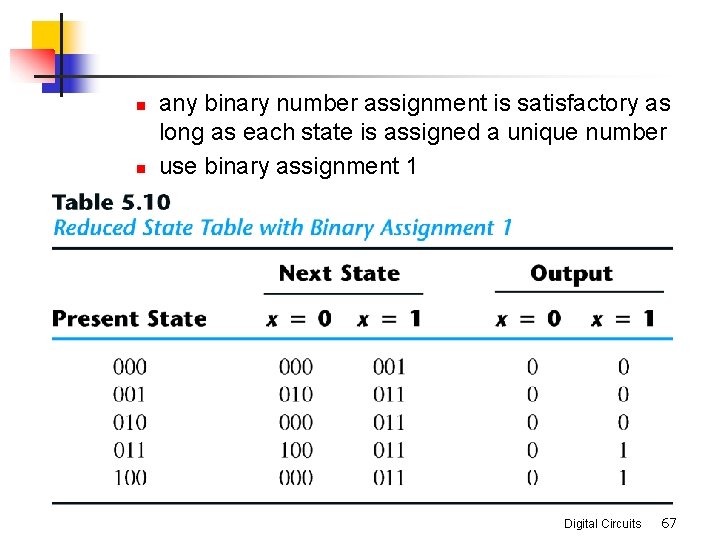
n n any binary number assignment is satisfactory as long as each state is assigned a unique number use binary assignment 1 Digital Circuits 67

5 -8 Design Procedure n n n n the word description of the circuit behavior (a state diagram) state reduction if necessary assign binary values to the states obtain the binary-coded state table choose the type of flip-flops derive the simplified flip-flop input equations and output equations draw the logic diagram Digital Circuits 68

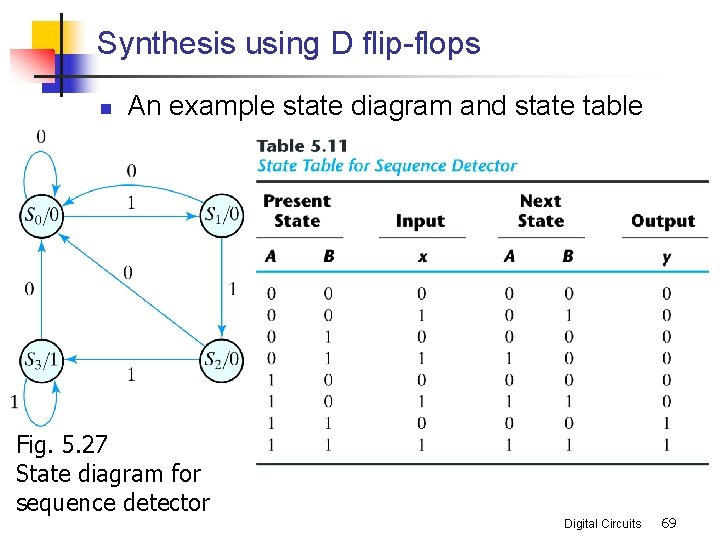
Synthesis using D flip-flops n An example state diagram and state table Fig. 5. 27 State diagram for sequence detector Digital Circuits 69

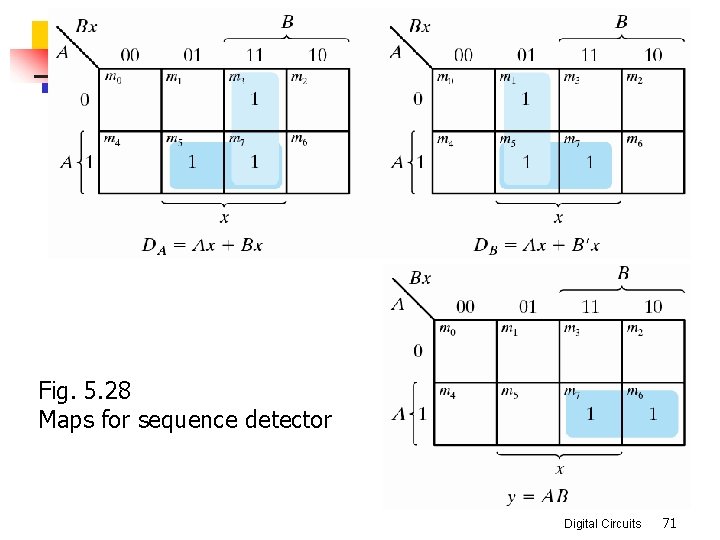
n The flip-flop input equations n n n The output equation n n A(t+1) = DA(A, B, x) = S(3, 5, 7) B(t+1) = DB(A, B, x) = S(1, 5, 7) y(A, B, x) = S(6, 7) Logic minimization using the K map n n n DA= Ax + Bx DB= Ax + B'x y = AB Digital Circuits 70

Fig. 5. 28 Maps for sequence detector Digital Circuits 71

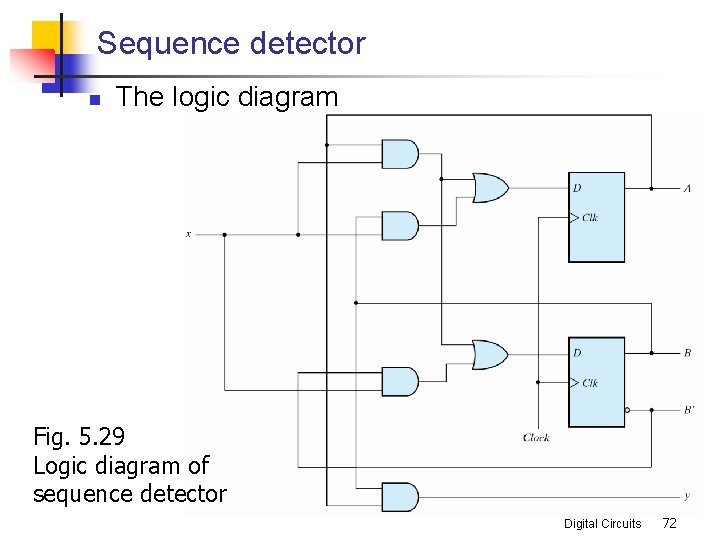
Sequence detector n The logic diagram Fig. 5. 29 Logic diagram of sequence detector Digital Circuits 72

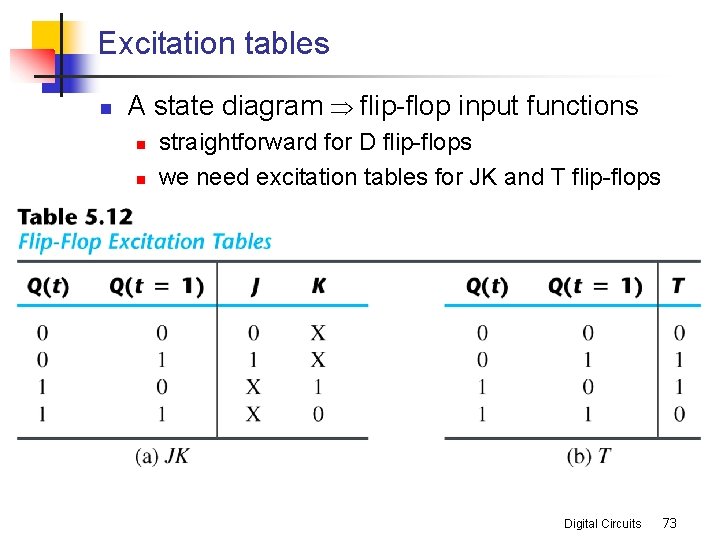
Excitation tables n A state diagram Þ flip-flop input functions n n straightforward for D flip-flops we need excitation tables for JK and T flip-flops Digital Circuits 73

Synthesis using JK flip-flops n n The same example The state table and JK flip-flop inputs Digital Circuits 74

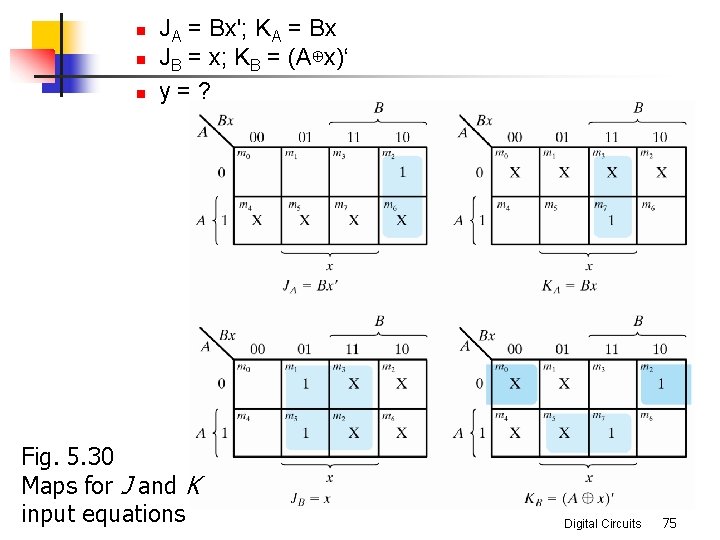
n n n JA = Bx'; KA = Bx JB = x; KB = (A⊕x)‘ y = ? Fig. 5. 30 Maps for J and K input equations Digital Circuits 75

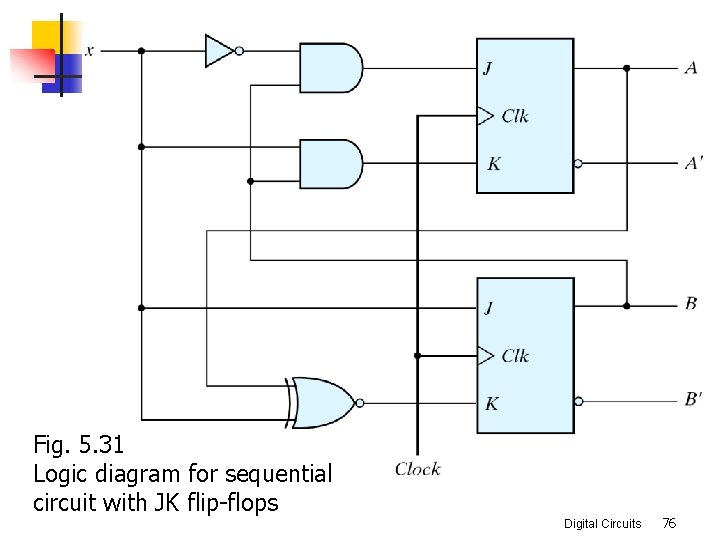
Fig. 5. 31 Logic diagram for sequential circuit with JK flip-flops Digital Circuits 76

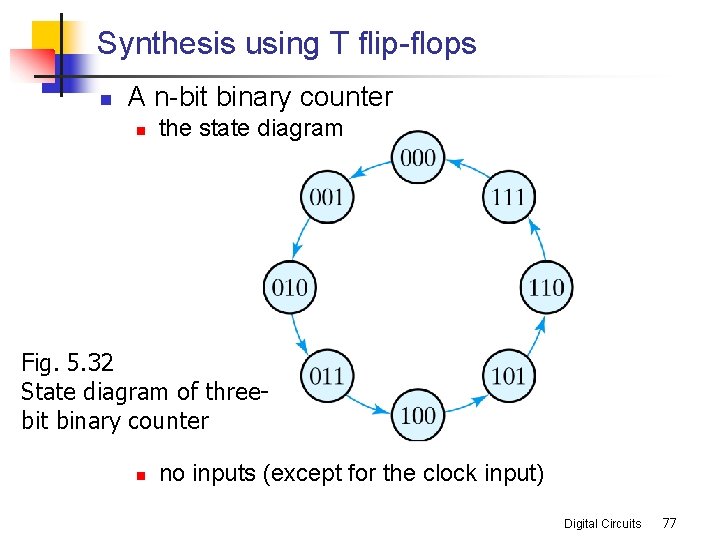
Synthesis using T flip-flops n A n-bit binary counter n the state diagram Fig. 5. 32 State diagram of threebit binary counter n no inputs (except for the clock input) Digital Circuits 77

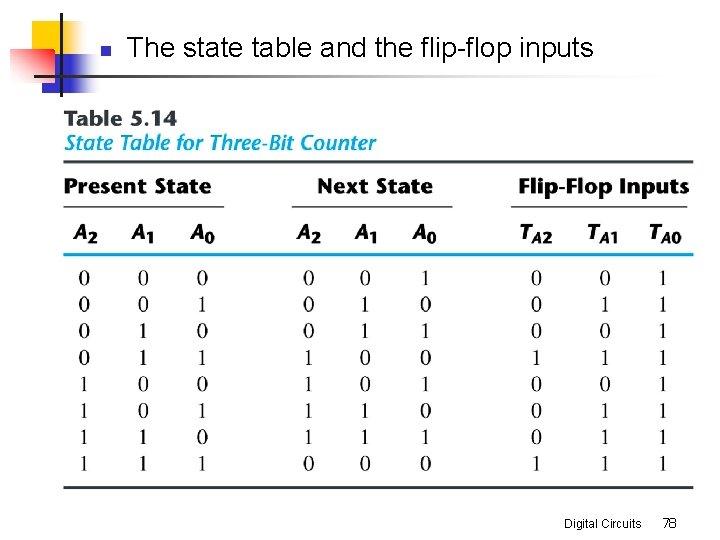
n The state table and the flip-flop inputs Digital Circuits 78

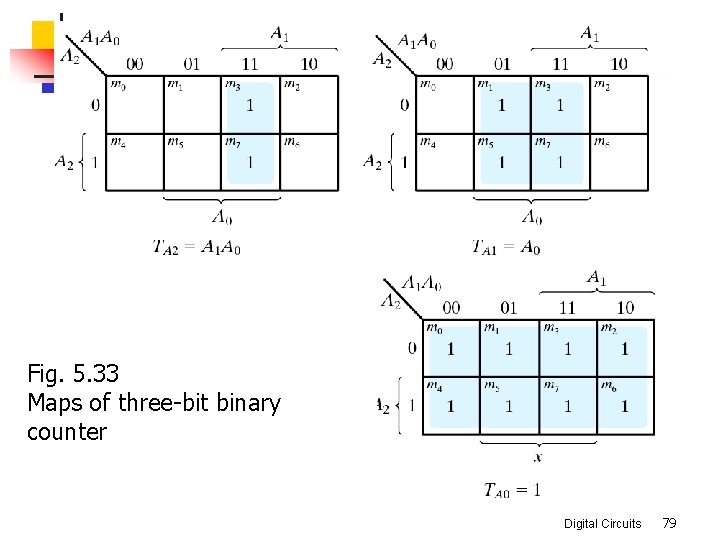
Fig. 5. 33 Maps of three-bit binary counter Digital Circuits 79

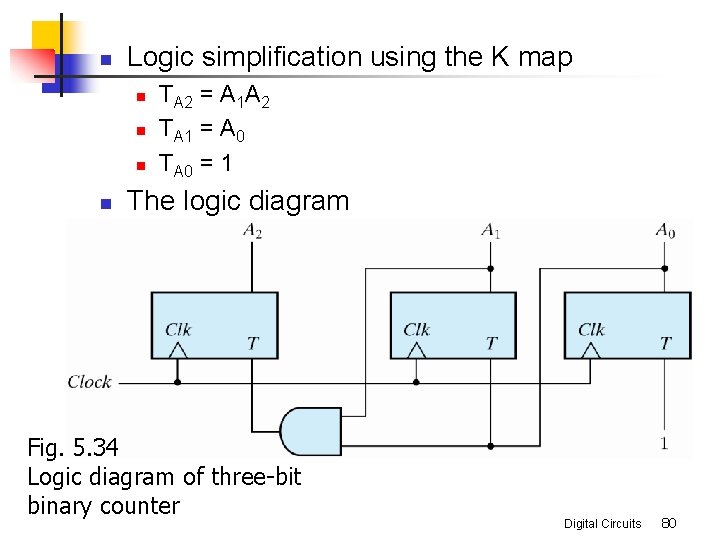
n Logic simplification using the K map n n TA 2 = A 1 A 2 TA 1 = A 0 TA 0 = 1 The logic diagram Fig. 5. 34 Logic diagram of three-bit binary counter Digital Circuits 80