Synchronous Computing SIMD Associative and Multi Associative Models

Synchronous Computing SIMD, Associative, and Multi. Associative Models Johnnie Baker

Synchronous Computing Topics • Introduction – References for Associative Computing – Motivation for the ASC model – The ASC and MASC Models – A Language Designed for the ASC Model – Two ASC Algorithms and Programs • ASC and MASC Algorithm Examples – ASC version of Prim’s MST Algorithm – ASC version of QUICKHULL – MASC version of QUICKHULL. 2

Associative Computing References Note: Below KSU papers are available on the website: http: //www. cs. kent. edu/~parallel/ (Click on the link to “papers”) 1. 2. Maher Atwah, Johnnie Baker, and Selim Akl, An Associative Implementation of Classical Convex Hull Algorithms, Proc of the IASTED International Conference on Parallel and Distributed Computing and Systems, 1996, 435 -438 Johnnie Baker and Mingxian Jin, Simulation of Enhanced Meshes with MASC, a MSIMD Model, Proc. of the Eleventh IASTED International Conference on Parallel and Distributed Computing and Systems, Nov. 1999, 511 -516. 3

Associative Computing References 3. Mingxian Jin, Johnnie Baker, and Kenneth Batcher, Timings for Associative Operations on the MASC Model, Proc. of the 15 th International Parallel and Distributed Processing Symposium, (Workshop on Massively Parallel Processing, San Francisco, April 2001. Jerry Potter, Johnnie Baker, Stephen Scott, Arvind Bansal, Chokchai Leangsuksun, and Chandra Asthagiri, An Associative Computing Paradigm, Special Issue on Associative Processing, IEEE Computer, 27(11): 19 -25, Nov. 1994. (Note: MASC is called ‘ASC’ in this article. ) 4. – 5. Primary Reference Jerry Potter, Associative Computing - A Programming Paradigm for Massively Parallel Computers, Plenum Publishing Company, 1992. 4

Associative Computers Associative Computer: A SIMD computer with a few additional features supported in hardware. • These additional features can be supported (less efficiently) in traditional SIMDs in software. • The name “associative” is due to its ability to locate items in the memory of PEs by content rather than location. 5

Associative Models The ASC model (for ASsociative Computing) lists the properties assumed for an associative computer. The MASC (for Multiple ASC) Model • Supports multiple SIMD (or MSIMD) computation. • Allows model to have more than one Instruction Stream (IS) – The IS corresponds to the control unit of a SIMD. • ASC is the MASC model with only one IS. – The one IS version of the MASC model is sufficiently important to have its own name. 6

ASC & MASC are KSU Models • Several professors and their graduate students at Kent State University have worked on models • The STARAN and the ASPRO computers fully support the ASC model in hardware. The MPP can easily support ASC but not in hardware. – Prof. Batcher was chief architect or consultant • Dr. Potter developed a language for ASC • Several of my students and I work on algorithms for models and architectures that support associative computing • Dr. Walker and his students have investigated a hardware design to support the ASC and MASC models. • Dr. Batcher and Dr. Potter are currently not actively working on ASC/MASC models but still provide advice. 7

Motivation • The STARAN Computer (Goodyear Aerospace, early 1970’s) and later the ASPRO provided the motivation for the ASC model. • ASC provides a parallel computational model that fully supports the “data parallel” style of programming. • ASC provides a practical model to support massive parallelism. • MASC supports allowing multiple ASC computations to occur concurrently. • Careful descriptions of these models allow them to be compared to other parallel models 8

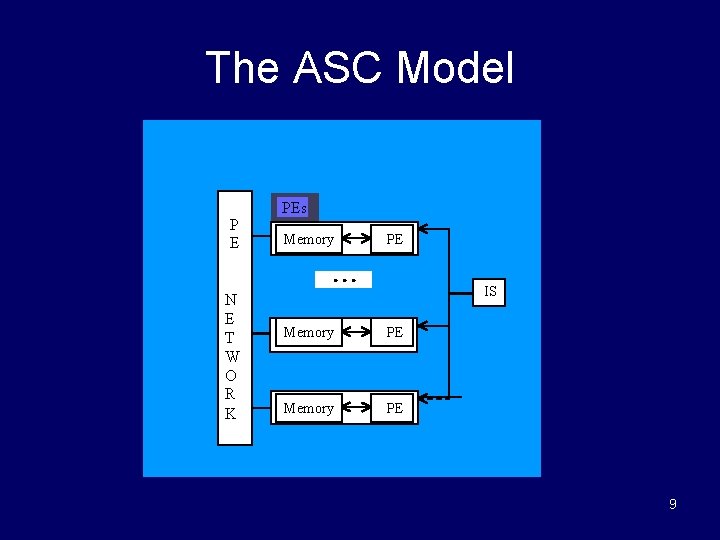
The ASC Model P E PEs Memory PE N E T W O R K IS Memory PE 9

Basic Properties of ASC • Instruction Stream – The IS has a copy of the program and broadcasts instructions to all PEs in unit time • PE Properties – Each PE has a local memory that is only accessible by its PE – All PEs listen to the IS – A PE can be active, inactive, or idle • Inactive PEs listens to but does not execute IS commands until reactivated • Idle PEs contain no essential data and are available for reassignment • Active PEs execute IS commands synchronously 10

Basic Properties of ASC • Responder Processing – The IS can detect if a data test is satisfied by any of its responder PEs in constant time (i. e. , any-responders property). – The IS can select an arbitrary responder in constant time (i. e. , pick-one property). 11

Basic Properties of ASC • Constant Time Global Operations (across PEs) – Logical OR and AND of binary values (reductions) – Maximum and minimum of numbers (reductions) – Associative searches • Communications – There at least two networks • PE communications network • IS broadcast/reduction network 12 – Can implemented as one network or two separate networks)

Basic Properties of ASC – The PE communications network is normally supported by an interconnection network • E. g. , a 2 D mesh – The broadcast/reduction network(s) can be supported by a broadcast and a reduction network of circuits (either 2 separate networks or 1 combined network). • See posted paper by Jin, Baker, & Batcher (listed in associative references) • Control Features – PEs, the IS, and the networks all operate synchronously, using the same clock 13

Non-SIMD Properties of ASC • Observation: The ASC properties that are unusual for SIMDs are the constant time operations: – Constant time responder processing • Any-responders? • Pick-one – Constant time global operations • Logical OR and AND of binary values • Maximum and minimum value of numbers • Associative Searches • These timings are justified by implementations using a resolver in the paper by Jin, Baker, & Batcher (listed in associative references and posted). 14

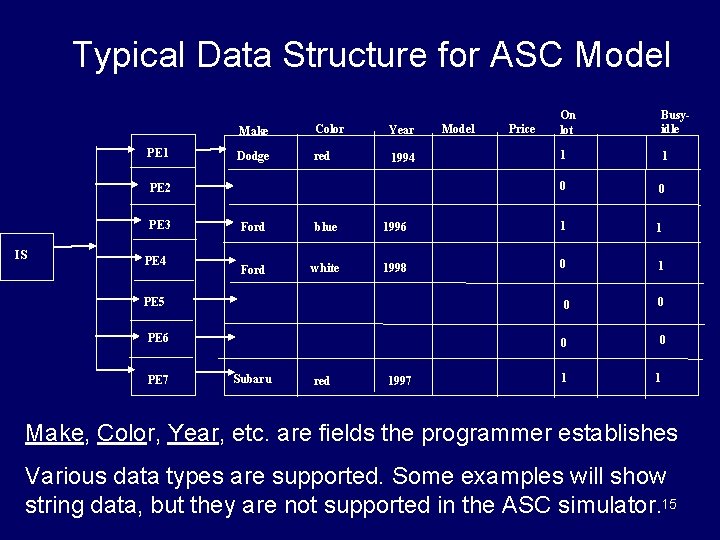
Typical Data Structure for ASC Model PE 1 Make Color Year Dodge red 1994 PE 2 PE 3 IS PE 4 Price Busyidle 1 1 0 0 Ford blue 1996 1 1 Ford white 1998 0 1 PE 5 PE 6 PE 7 Model On lot Subaru red 1997 0 0 1 1 Make, Color, Year, etc. are fields the programmer establishes Various data types are supported. Some examples will show string data, but they are not supported in the ASC simulator. 15

The Associative Search PE 1 Make Color Year Dodge red 1994 Model Price PE 2 PE 3 IS PE 4 Busyidle 1 1 0 0 Ford blue 1996 1 1 Ford white 1998 0 1 PE 5 PE 6 PE 7 On lot Subaru red 1997 0 0 1 1 IS asks for all cars that are red and on the lot. PE 1 and PE 7 respond by setting a mask bit in their PE. 16

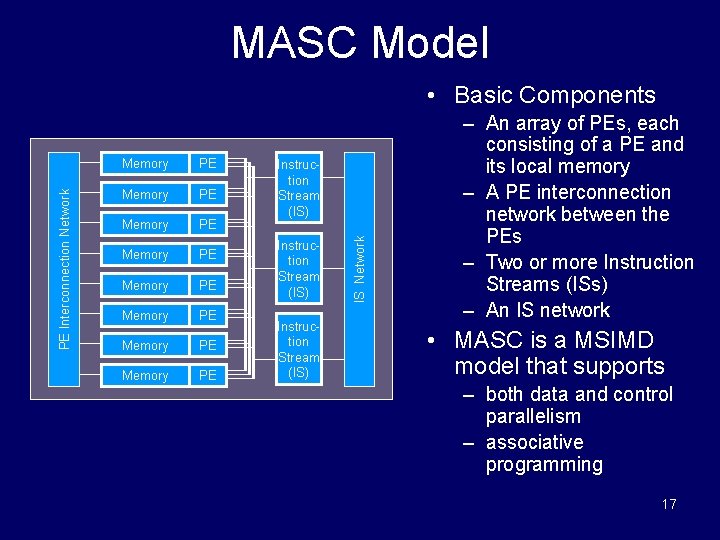
MASC Model Memory PE Memory PE Instruction Stream (IS) IS Network PE Interconnection Network • Basic Components – An array of PEs, each consisting of a PE and its local memory – A PE interconnection network between the PEs – Two or more Instruction Streams (ISs) – An IS network • MASC is a MSIMD model that supports – both data and control parallelism – associative programming 17

MASC Basic Properties • Each PE can listen to only one IS • PEs can switch ISs in unit time, based on the results of a data test. • Each IS and the PEs listening to it follow rules of the ASC model. • Control Features: – The PEs, ISs, and networks all operate synchronously, using the same clock – A master IS coordinates the interaction between the multiple ISs. 18

Characteristics of Associative Programming • Consistent use of style of programming called data parallel programming • Consistent use of global associative searching and responder processing • Usually, frequent use of the constant time global reduction operations: AND, OR, MAX, MIN • Broadcast of data using IS bus allows the use of the PE network to be restricted to parallel data movement. 19

Characteristics of Associative Programming • • Tabular representation of data – (i. e. , 2 D arrays) Use of searching instead of sorting Use of searching instead of pointers Use of searching instead of the ordering provided by linked lists, stacks, queues • Promotes an highly intuitive programming style that promotes high productivity • Uses structure codes (i. e. , numeric representation) to represent data structures such as trees, graphs, embedded lists, and matrices. • Examples of use of structure codes are given in – Ref: Nov. 1994 IEEE Computer article (see references) – Extensive uses in “Associative Computing” book by Jerry Potter. 20

Languages Designed for the ASC • Professor Potter has created several languages for the ASC model. • ASC is a C-like language designed for ASC model – Compilers and instructions posted under “software” • ACE is a higher level language than ASC that uses natural language syntax; e. g. , plurals, pronouns (e. g. , “its”, “their”, etc. ) • Language References: – ASC Primer – Copy available on parallel lab website www. cs. kent. edu/~parallel/ under “software”. – “Associative Computing” book by Potter [11] – some features in this book were never fully implemented in his ASC compiler 21

Algorithms and Programs Implemented in ASC • A wide range of algorithms implemented in ASC without the use of the PE network: – Graph Algorithms • minimal spanning tree • shortest path • connected components – Computational Geometry Algorithms • convex hull algorithms (Jarvis March, Quickhull, Graham Scan, etc) • Dynamic hull algorithms 22

ASC Algorithms and Programs (not requiring PE network) – String Matching Algorithms • all exact substring matches • all exact matches with “don’t care” (i. e. , wild card) characters. – Algorithms for NP-complete problems • traveling salesperson • 2 -D knapsack. – Data Base Management Software • associative data base • relational data base 23

ASC Algorithms and Programs (not requiring a PE network) – A Two Pass Compiler for ASC – not the one we will be using. This compiler runs on an associative computer & uses ASC parallelism. • first pass • optimization phase – Two Rule-Based Inference Engines for AI • An Expert System OPS-5 interpreter • PPL (Parallel Production Language interpreter) – A Context Sensitive Language Interpreter • (OPS-5 variables force context sensitivity) – An associative PROLOG interpreter 24

Associative Algorithms & Programs (using a network) • There are numerous associative algorithms or programs that use a PE network; – 2 -D Knapsack ASC Algorithm using a 1 -D mesh – Image processing algorithms using 1 -D mesh – FFT (Fast Fourier Transform) using 1 -D nearest neighbor & Flip networks – Matrix Multiplication using 1 -D mesh – An Air Traffic Control Program (used a Flip network connection between PEs and memory) • Demonstrated using live data at Dulles Field in early 70’s. • All but first were created and/or implemented in assembler for STARAN at Goodyear Aerospace 25

Example 1 - MST • A graph has nodes labeled by some identifying letter or number and arcs which are directional and have weights associated with them. • Such a graph could represent a map where the nodes are cities and the arc weights give the mileage between two cities. 3 A B 5 2 C D 4 E 5 26

The MST Problem • The MST problem assumes the weights are positive and the graph is undirected and connected. The goal is to find a minimal spanning tree, – i. e. a subgraph that is a tree 1, that includes all nodes (i. e. it spans), and – where the sum of the weights on the arcs of the subgraph is the smallest possible weight (i. e. it is minimal). • Why would an algorithm solving this problem be useful? • Note: The solution may not be unique. 1 A tree is a set of points called vertices, pairs of distinct vertices called edges, such that (1) there is a path from any vertex to any other, and (2) there are no circuits (i. e. , that is, no paths starting from a vertex and returning to 27 the same vertex).

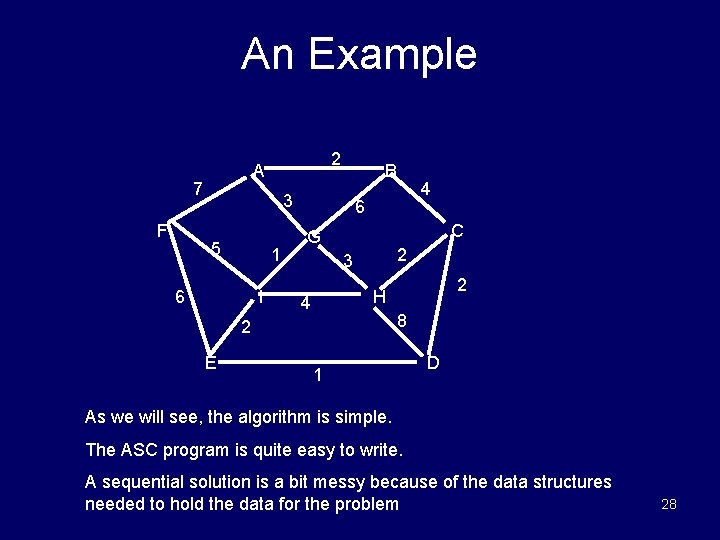
An Example 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D As we will see, the algorithm is simple. The ASC program is quite easy to write. A sequential solution is a bit messy because of the data structures needed to hold the data for the problem 28

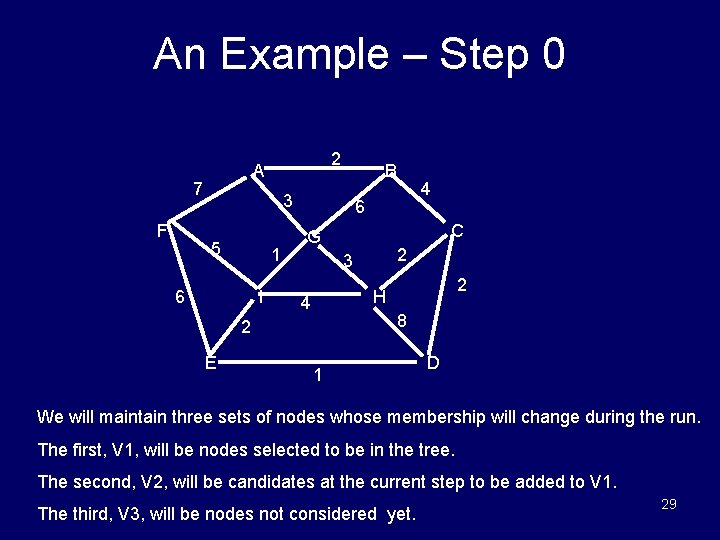
An Example – Step 0 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D We will maintain three sets of nodes whose membership will change during the run. The first, V 1, will be nodes selected to be in the tree. The second, V 2, will be candidates at the current step to be added to V 1. The third, V 3, will be nodes not considered yet. 29

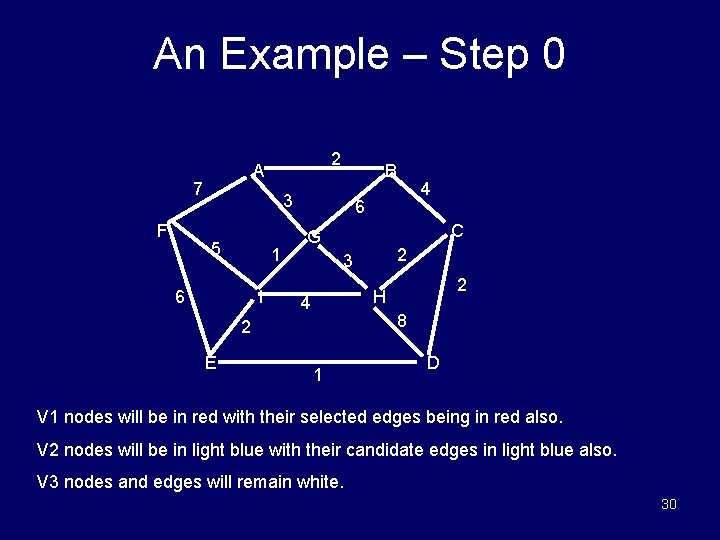
An Example – Step 0 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D V 1 nodes will be in red with their selected edges being in red also. V 2 nodes will be in light blue with their candidate edges in light blue also. V 3 nodes and edges will remain white. 30

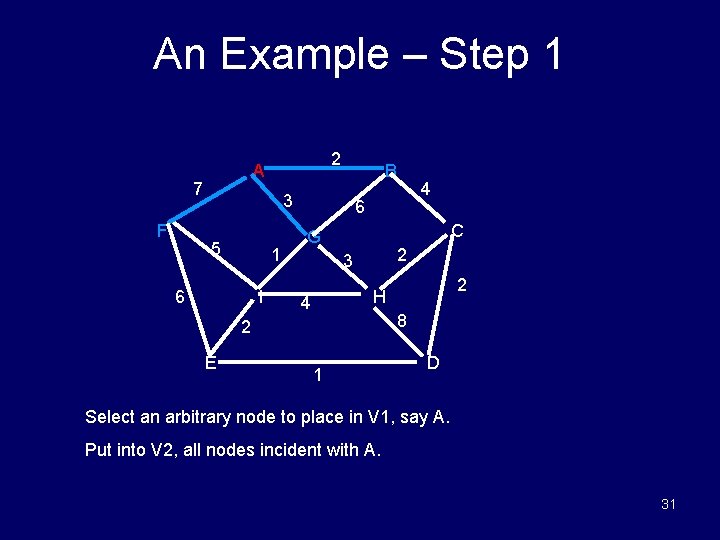
An Example – Step 1 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D Select an arbitrary node to place in V 1, say A. Put into V 2, all nodes incident with A. 31

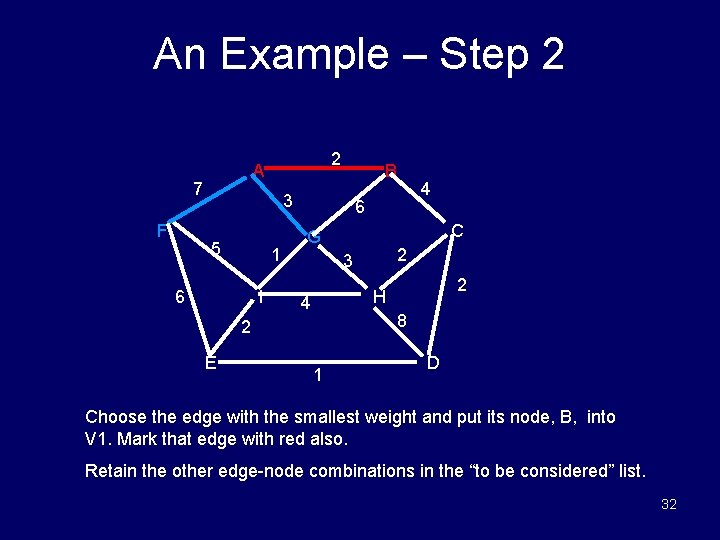
An Example – Step 2 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D Choose the edge with the smallest weight and put its node, B, into V 1. Mark that edge with red also. Retain the other edge-node combinations in the “to be considered” list. 32

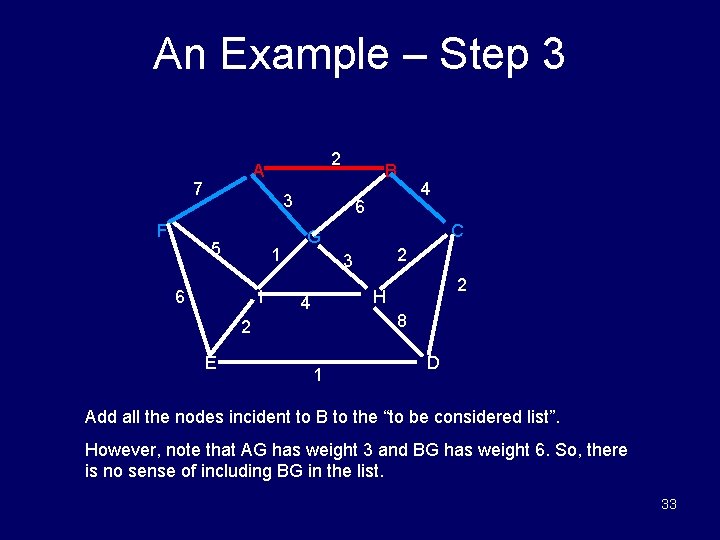
An Example – Step 3 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D Add all the nodes incident to B to the “to be considered list”. However, note that AG has weight 3 and BG has weight 6. So, there is no sense of including BG in the list. 33

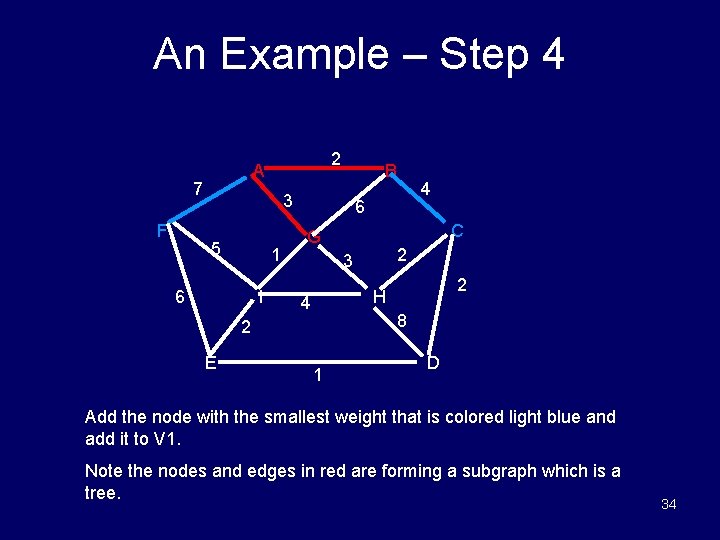
An Example – Step 4 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D Add the node with the smallest weight that is colored light blue and add it to V 1. Note the nodes and edges in red are forming a subgraph which is a tree. 34

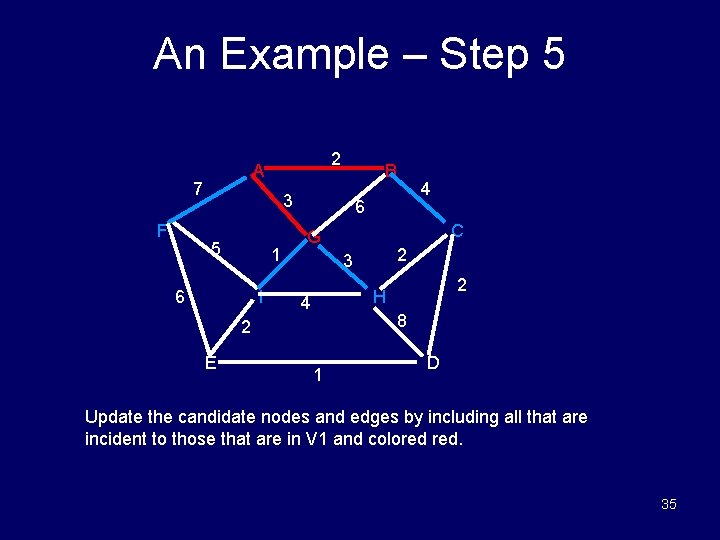
An Example – Step 5 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D Update the candidate nodes and edges by including all that are incident to those that are in V 1 and colored red. 35

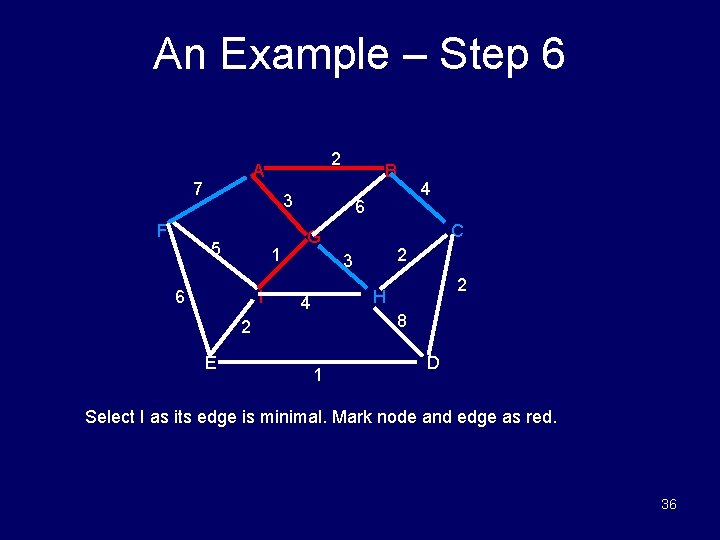
An Example – Step 6 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D Select I as its edge is minimal. Mark node and edge as red. 36

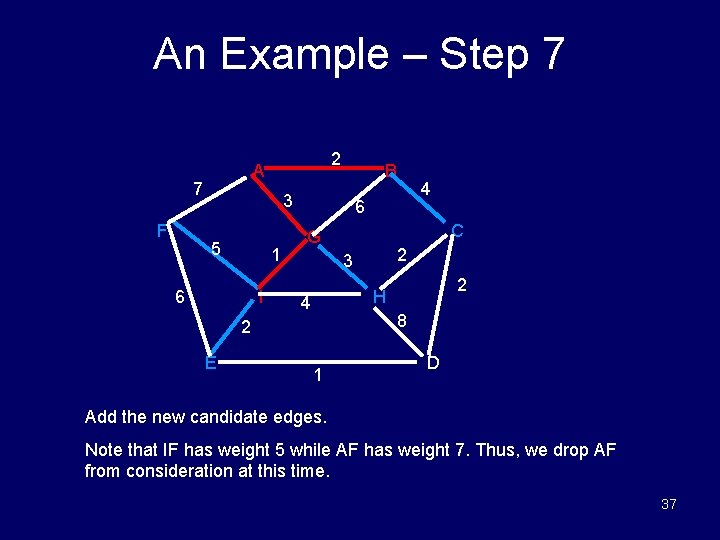
An Example – Step 7 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D Add the new candidate edges. Note that IF has weight 5 while AF has weight 7. Thus, we drop AF from consideration at this time. 37

An Example – after several more passes, C is added & we have … 7 F 2 A B 3 5 1 6 I 6 C G 2 3 2 H 4 8 2 E 4 1 D Note that when CH is added, GH is dropped as CH has less weight. Candidate edge BC is also dropped since it would form a back edge between two nodes already in the MST. When there are no more nodes to be considered, i. e. no more in V 3, we obtain the final solution. 38

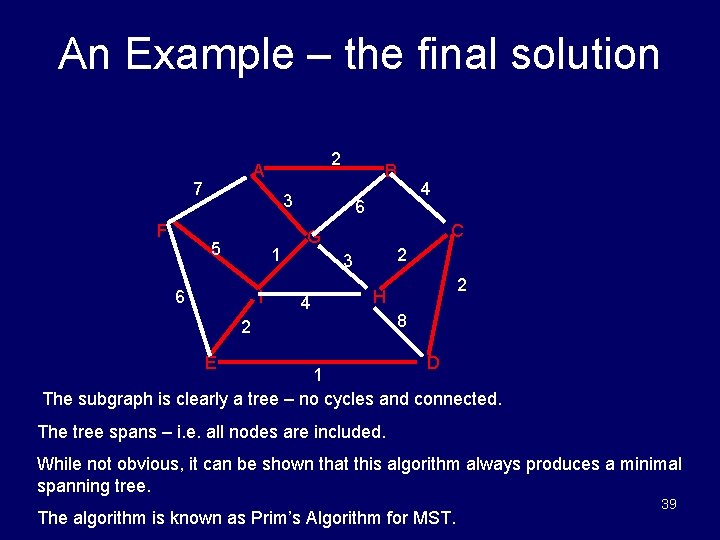
An Example – the final solution 7 F 2 A B 3 5 1 6 I 4 6 C G 2 3 4 2 H 2 8 E D 1 The subgraph is clearly a tree – no cycles and connected. The tree spans – i. e. all nodes are included. While not obvious, it can be shown that this algorithm always produces a minimal spanning tree. The algorithm is known as Prim’s Algorithm for MST. 39

The ASC Program vs a sequential solution in C, C++, or Java • First, think about how you would write the program in C or C++. • The usual solution uses some way of maintaining the sets as lists using pointers or references. – See solutions to MST in Algorithms texts by Baase in the posted references. • In the ASC language, pointers are not even supported as they are not needed and their use is likely to result in inefficient SIMD algorithms • An ASC algorithm will be developed for Prim’s sequential algorithm using a pseudocode that is based on the ASC language. • The ASC language user’s guide is posted at www. cs. kent. edu/~parallel/, but its use is not required. • The ASC algorithm can be used to create a program in 40 ASC for the ASC simulator or in Cn for Clear. Speed.

ASC-MST Algorithm Preliminaries • Next, a “data structure” level presentation of Prim’s algorithm for the MST is given. • The data structure used is illustrated in the next two slides. – This example is from the Nov. 1994 IEEE Computer paper cited in the references. • There are two types of variables for the ASC model, namely – the parallel variables (i. e. , ones for the PEs) – the scalar variables (ie. , the ones used by the IS). – Scalar variables are essentially global variables. • Could replace each scalar variable with its scalar value stored in each entry of a parallel variable. 41

ASC-MST Algorithm Preliminaries (cont. ) • In order to distinguish between variable types here, the parallel variables names will end with a “$” symbol. • Each step in this algorithm takes constant time. • One MST edge is selected during each pass through the loop in this algorithm. • Since a spanning tree has n-1 edges, the running time of this algorithm is O(n) and its cost is O(n 2). – Definition of cost is (running time) (number of processors) • Since the sequential running time of the Prim MST algorithm is O(n 2) and is time optimal, this parallel implementation is cost optimal. – Cost & optimality will be covered in parallel algorithm performance evaluation chapter (See Ch 7 of Quinn) 42

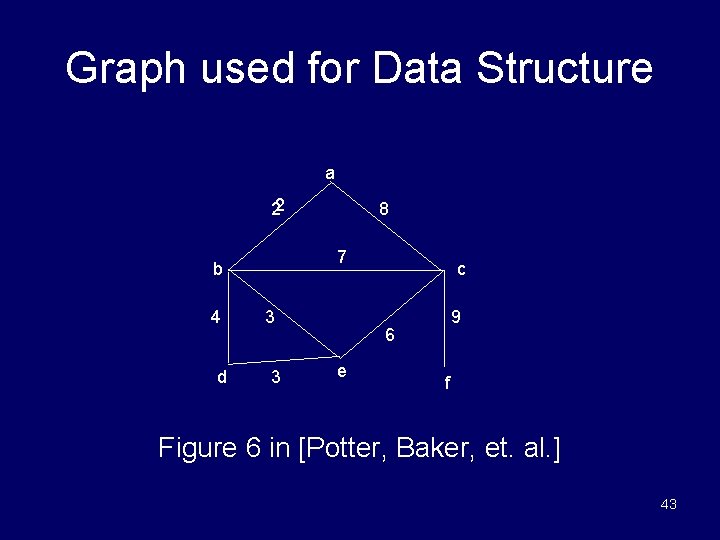
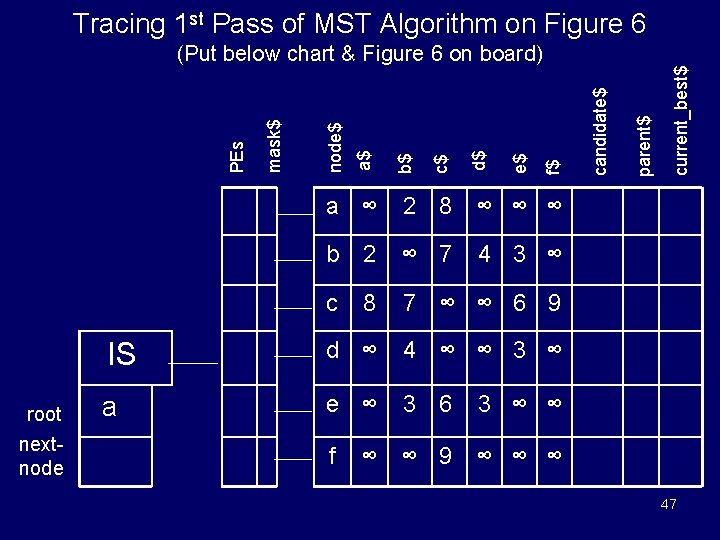
Graph used for Data Structure a 22 7 b 4 d 8 3 3 c 9 6 e f Figure 6 in [Potter, Baker, et. al. ] 43

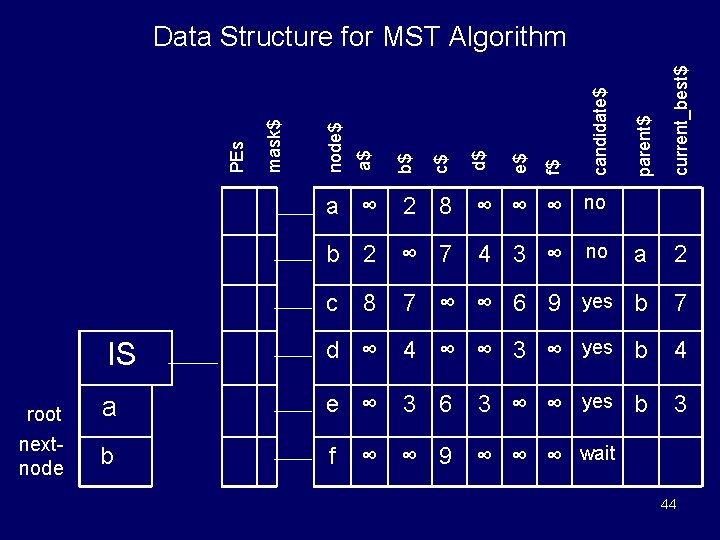
current_best$ 7 IS d ∞ 4 ∞ ∞ 3 ∞ yes b 4 root a e ∞ 3 6 3 ∞ ∞ yes b 3 nextnode b f candidate$ 7 ∞ ∞ 6 9 yes b f$ 8 e$ c d$ 2 c$ a b$ ∞ 7 a$ b 2 node$ 2 8 ∞ ∞ ∞ no mask$ a ∞ PEs parent$ Data Structure for MST Algorithm 4 3 ∞ no ∞ ∞ 9 ∞ ∞ ∞ wait 44

Short Version of Algorithm: ASC-MST-PRIM(root) 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Initialize candidates to “waiting” If there any finite values in root’s field, set candidate$ to “yes” set parent$ to root set current_best$ to the values in root’s field set root’s candidate field to “no” Loop while some candidate$ contain “yes” for them restrict mask$ to mindex(current_best$) set next_node to a node identified in the preceding step set its candidate to “no” if the value in their next_node’s field are less than current_best$, then set current_best$ to value in next_node’s field set parent$ to next_node if candidate$ is “waiting” and the value in its next_node’s field is finite set candidate$ to “yes” set parent$ to next_node 45 set current_best to the values in next_node’s field

Comments on ASC-MST Algorithm • The three preceding slides are Figure 6 in [Potter, Baker, et. al. ] IEEE Computer, Nov 1994]. • Preceding slide gives a compact, data-structures level pseudo-code description for this algorithm – Pseudo-code illustrates Potter’s use of pronouns (e. g. , them, its) and possessive nouns. – The mindex function returns the index of a processor holding the minimal value. – This MST pseudo-code is much shorter and simpler than data-structure level sequential MST pseudocodes • e. g. , see one of Baase’s textbooks cited in references • Algorithm given in Baase’s books is identical to this parallel algorithm, except for a sequential computer • Next, a more detailed explanation of the algorithm in preceding slide will be given next. 46

Tracing 1 st Pass of MST Algorithm on Figure 6 root nextnode a ∞ 2 8 ∞ ∞ ∞ b 2 ∞ 7 c 8 7 ∞ ∞ 6 9 IS d ∞ 4 ∞ ∞ 3 ∞ a e ∞ 3 6 f current_best$ parent$ candidate$ f$ e$ d$ c$ b$ a$ node$ mask$ PEs (Put below chart & Figure 6 on board) 4 3 ∞ ∞ ∞ ∞ 9 ∞ ∞ ∞ 47

Algorithm: ASC-MST-PRIM • Initially assign any node to root. • All processors set – candidate$ to “wait” – current-best$ to – the candidate field for the root node to “no” • All processors whose distance d from their node to root node is finite do – Set their candidate$ field to “yes – Set their parent$ field to root. – Set current_best$ = d. 48

Algorithm: ASC-MST-PRIM (cont. 2/3) • While the candidate field of some processor is “yes”, – Restrict the active processors to those whose candidate field is “yes” and (for these processors) do • Compute the minimum value x of current_best$. • Restrict the active processors to those with current_best$ = x and do – pick an active processor, say node y. » Set the candidate$ value of node y to “no” – Set the scalar variable next-node to y. 49

Algorithm: ASC-MST-PRIM (cont. 3/3) – If the value z in the next_node column of a processor is less than its current_best$ value, then » Set current_best$ to z. » Set parent$ to next_node – For all processors, if candidate$ is “waiting” and the distance of its node from next_node y is finite, then • Set candidate$ to “yes” • Set current_best$ to the distance of its node from y. • Set parent$ to y 50

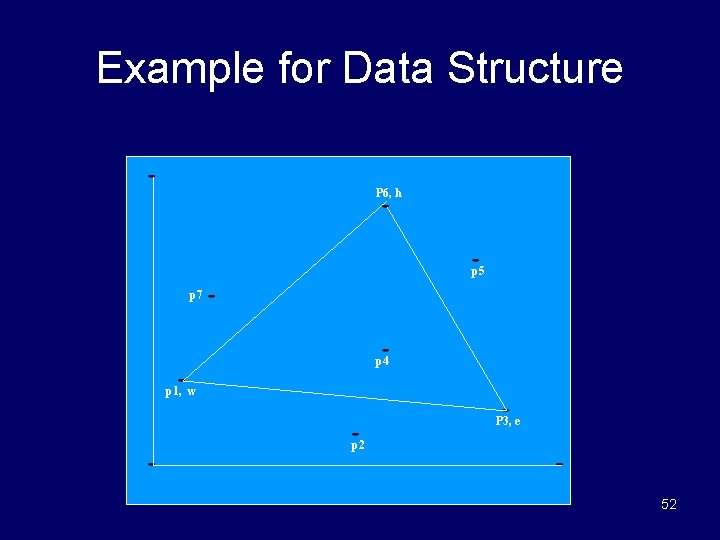
Quickhull Algorithm for ASC Reference: • Maher, Baker, Akl, “An Associative Implementation of Classical Convex Hull Algorithms” Sequential Quickhull Algorithm: h • Initial Steps – Label a point with the smallest x-value as w and a point with a largest x-value as e – Suffices to find the upper convex hull of points on or above the line from w to e. • Select a point h so that the area of triangle weh is maximal. • Eliminate points inside triangle • Proceed recursively with the sets of points on or above the lines and. e w 51

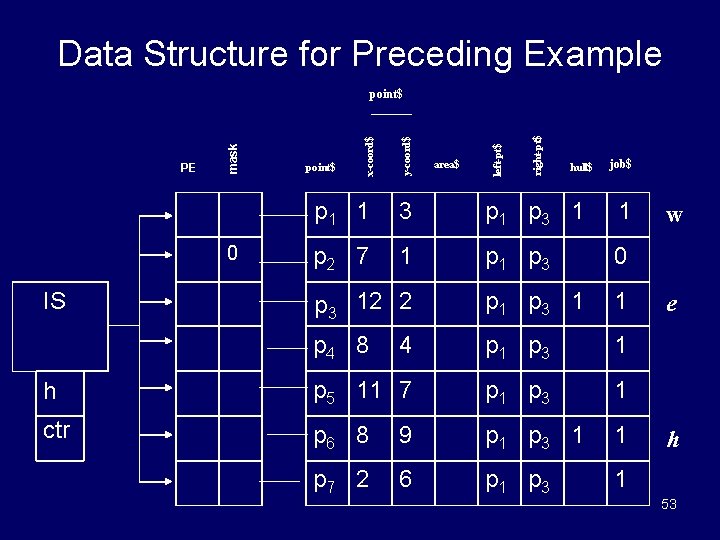
Example for Data Structure P 6, h p 5 p 7 p 4 p 1, w P 3, e p 2 52

Data Structure for Preceding Example right-pt$ area$ left-pt$ y-coord$ point$ x-coord$ PE mask point$ hull$ job$ p 1 1 3 p 1 p 3 1 1 p 2 7 1 p 3 0 p 3 12 2 p 1 p 3 1 1 p 4 8 4 p 1 p 3 1 h p 5 11 7 p 1 p 3 1 ctr p 6 8 9 p 1 p 3 1 1 p 7 2 6 p 1 p 3 1 0 IS w e h 53

Algorithms & Assumption • Basic algorithms exist for the following problems in Euclidean geometry for plane: – Determine whether a third point lies on, above, or below the line determined by two other points. – Compute the area of a triangle determined by three points. • Standard Computational Geometry Assumptions – No three points lie on the same line. – No two points have the same x-coord. & y-coord. Reference: Introduction to Algorithms by Cormen, Leisterson, Rivest, (& Stein), Mc. Graw Hill, Chapter on Computational Geometry. 54

ASC Quickhull Algorithm (Upper Convex Hull) ASC-Quickhull( planar-point-set ) 1. Initialize: ctr = 1, area$ = 0, hull$ = 0 2. Find the PE with the minimal x-coord$ and let w be its point$ a) Set its hull$ value to 1 3. Find the PE with maximal x-coord$ and let e be its point$ a) Set its hull$ to 1 4. All PEs set their left-pt to w and right-pt to e. 5. If the point$ for a PE lies above the line a) Then set its job$ value to 1 b) Else set its job$ value to 0 55

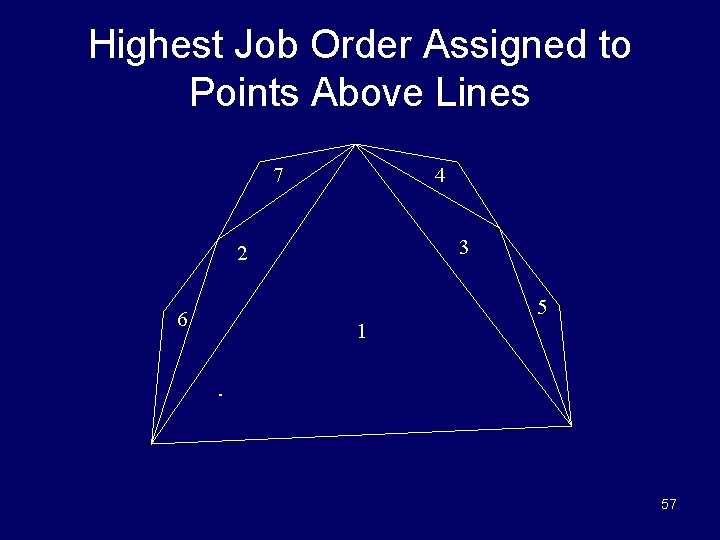
ASC Quickhull Algorithm (cont) 6. Loop while parallel job$ contains a nonzero value a) The IS makes its active PEs those with a maximal job$ value. b) Each (active) PE computes and stores the area of triangle (left-pt$, right-pt$, point$ ) in area$ c) Find the PE with the maximal area$ and let h be its third point. • Set its hull$ value to 1 d) Each PE whose point$ is above • • sets its job$ value to ++ctr sets its right-pt to h e) Each PE whose point$ is above • • f) sets its job$ to ++ctr sets its left-pt to h Each PE with job$ < ctr -2 sets its job$ value to 0 56

Highest Job Order Assigned to Points Above Lines 7 4 3 2 5 6 1 57

Order that Triangles are Computed 6 4 2 5 3 7 1 58

Performance of ASC-Quickhull Average Case: • Assume either one of the following: – For some integer k>1, on average 1/k of the points above each line being processed are eliminated each round. • For example, if k = 3, then one of the three different areas are eliminated each round – O(lg n) points are on the convex hull. • For randomly generated points, the number of convex hull points has been shown to be almost exactly lg(n) points. 59

Performance of ASC-Quickhull (cont) • Either of above assumptions imply the average running time is O(lg n). – True since each pass through algorithm loop produces one convex hull point. • The average cost is O(n lg n) Worst Case: • Running time is O(n). • Cost is O(n 2) Recall: The definition of cost is Cost = (running time) (nr. of processors) 60

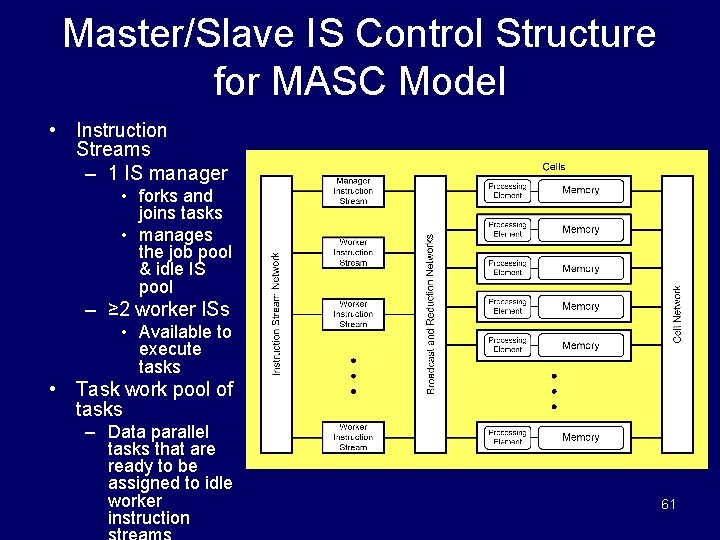
Master/Slave IS Control Structure for MASC Model • Instruction Streams – 1 IS manager • forks and joins tasks • manages the job pool & idle IS pool – ≥ 2 worker ISs • Available to execute tasks • Task work pool of tasks – Data parallel tasks that are ready to be assigned to idle worker instruction 61

Master/Slave IS Control Structure for the MASC Model • The master IS is connected to each worker IS by an IS broadcast/reduction network. – A more minimal network may also be adequate, especially when the number of worker ISs is not large. – Efficient communications need to be supported between the master IS and each worker IS. The data size of these communications is small. – Worker ISs do not need to communicate with each other. • The master IS maintains a pool of unassigned jobs and a pool of idle ISs • A job consists of a task to be performed and the idle PEs which will perform this job. • When the job and IS pools are both nonempty, the master IS will assign a job to an idle worker IS. • An active IS will return any jobs it creates that need to be reassigned to the master IS to place in job pool. 62

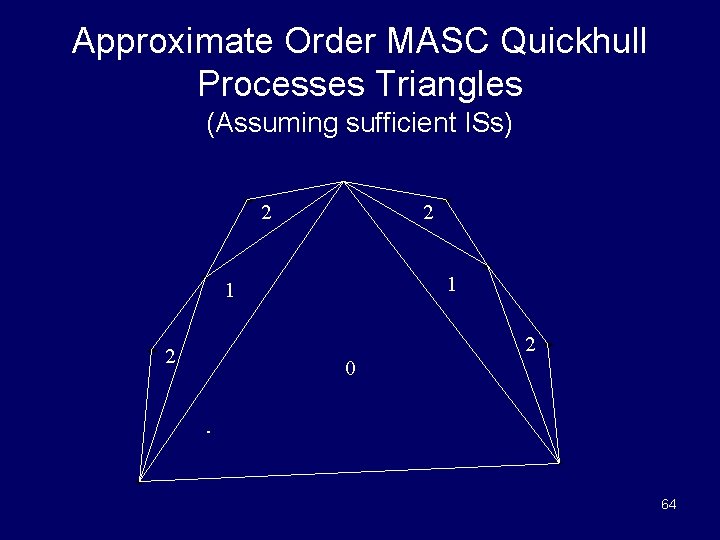
MASC Quickhull Algorithm MASC Modification of ASC Quickhull Algorithm: 1. Initially, the master IS executes the initialization phase of the ASC Quicksort, using all the PEs. • Alternately, it could assign one worker IS to do this. 2. The master IS maintains the scalar variable “ctr”. When the job pool and the IS pool are both nonempty, the master IS will assign a job to an IS. 3. Each IS computes the steps in the loop in ASCQuickhull. If two jobs are created, one is added to the job pool. • If a job is added to the job pool, the value in the ctr scalar variable is assigned as the job number and the Master IS increments the ctr variable. 4. The algorithm will terminate when there are no more jobs in the job pool and all ISs are idle. 63

Approximate Order MASC Quickhull Processes Triangles (Assuming sufficient ISs) 2 2 1 1 2 2 0 64

Analysis for MASC Quickhull Average Case: • Assumptions: – The remaining unidentified hull points are roughly evenly distributed among the partitions in each recursive level – O(lg n) Instruction Streams are available. – There are O(lg n) convex hull points • The time for master IS to assign a task to an IS is a small constant and this time will be included with the time required to execute the task. • The average running time is O(lg lg n) and the average cost is O(n lg lg n). • O(lg lg n) increases so slowly that it is essentially 65 a constant for practical values of n.

Analysis for MASC Quickhull (cont) Worst Case • O(n) – Happens if all points are hull points and all remaining points always lie on one side of each triangle selected. • E. g. , all points lie on a non-horizonal line above the x-y axis. – Also, can happen if most of the points are hull points • E. g. , if all but a constant number of triangles selected have all of the remaining points they are assigned to lie on one side of the triangle. • Bad Case which is O(lg n) – All points are hull points, so only one point can be eliminated each time code is executed. 66

Comments on MASC Quickhull • For one million randomly generated points, this algorithm would require a maximum of lg n = 20 ISs on any level. – Note that 33. 5 million randomly generated points only requires 25 ISs at each level, or 5 more than required for 1 million – By using virtual IS-parallelism, fewer ISs can be used. • Even if (lg n) ISs are available for this algorithm, there may be occasions during execution when the IS pool is empty and the job pool is non-empty. • This algorithm will provide a nice speedup, even if only a small constant number k>0 of ISs are available. – The complexity of the running time only be O(lg n). – However, the actual running time should be close to k times faster than for one IS. – There will be a small loss of efficiency due to IS interactions. • This algorithm works, whether or not sufficient ISs are available. 67

Additional Comments on ASC and MASC Algorithms • The full “convex hull” algorithm requires that an ordered (e. g. , clockwise) list of convex hull points be returned. – Preceding algorithms for ASC and MASC can be extended to handle this. • This detail is omitted here to keep the algorithms simpler. – More information can be found in the paper “An Associative Implementation of Classical Convex Hull Algorithms” by Atwah, Baker, and Akl and in Maher Atwah’s master’s thesis at KSU. 68

END OF SLIDE SET