Synchronization Using PhaseLocked Loops Example 16 1 Multiplexer

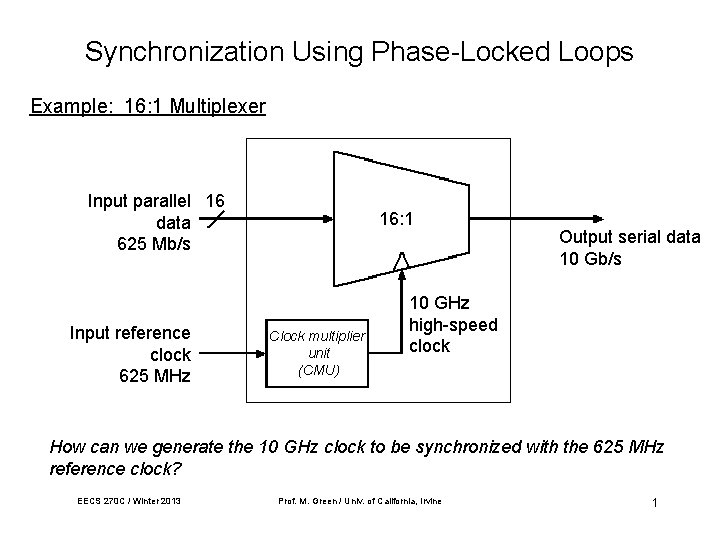
Synchronization Using Phase-Locked Loops Example: 16: 1 Multiplexer Input parallel 16 data 625 Mb/s Input reference clock 625 MHz 16: 1 Clock multiplier unit (CMU) Output serial data 10 Gb/s 10 GHz high-speed clock How can we generate the 10 GHz clock to be synchronized with the 625 MHz reference clock? EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 1

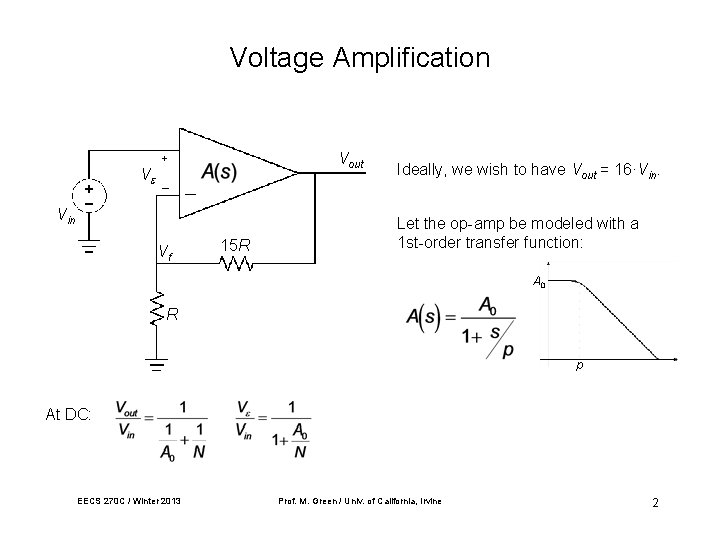
Voltage Amplification V Vout + _ Vin Vf 15 R Ideally, we wish to have Vout = 16·Vin. Let the op-amp be modeled with a 1 st-order transfer function: A 0 R p At DC: EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 2

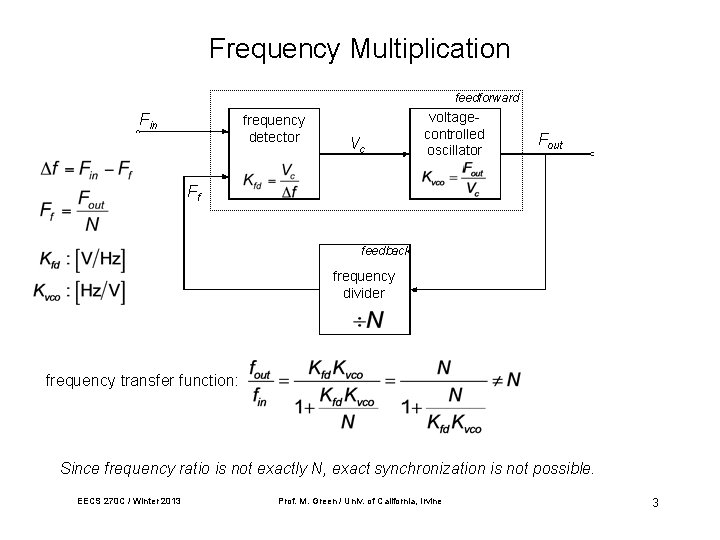
Frequency Multiplication feedforward Fin frequency detector Vc voltagecontrolled oscillator Fout Ff feedback frequency divider frequency transfer function: Since frequency ratio is not exactly N, exact synchronization is not possible. EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 3

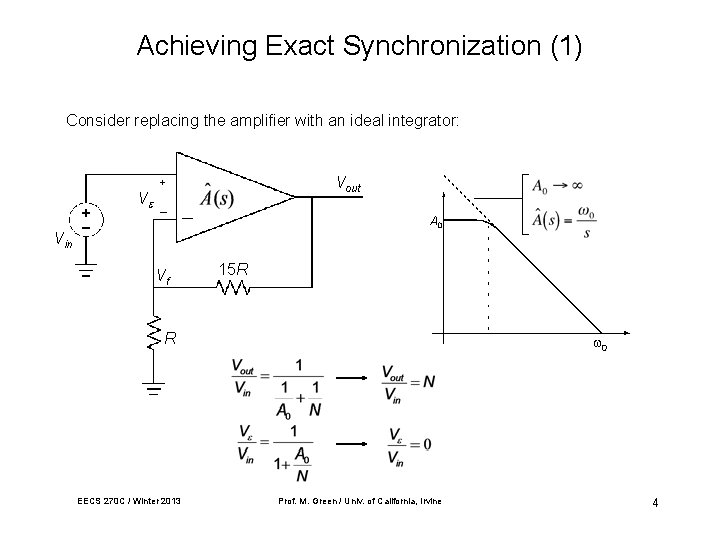
Achieving Exact Synchronization (1) Consider replacing the amplifier with an ideal integrator: V Vout + _ A 0 Vin Vf 15 R R EECS 270 C / Winter 2013 0 Prof. M. Green / Univ. of California, Irvine 4

Achieving Exact Synchronization (2) Consider a sine function: Define instantaneous angular frequency: If we can arrange to have the detector respond to phase difference (instead of frequency difference), then integration is naturally introduced into the loop. . . EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 5

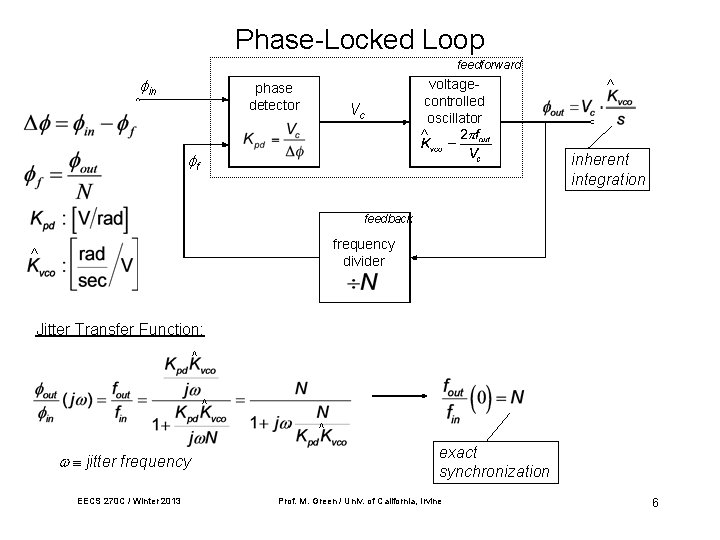
Phase-Locked Loop feedforward in phase detector Vc voltagecontrolled oscillator ^ ^ f inherent integration feedback frequency divider ^ Jitter Transfer Function: ^ ^ ^ jitter frequency EECS 270 C / Winter 2013 exact synchronization Prof. M. Green / Univ. of California, Irvine 6

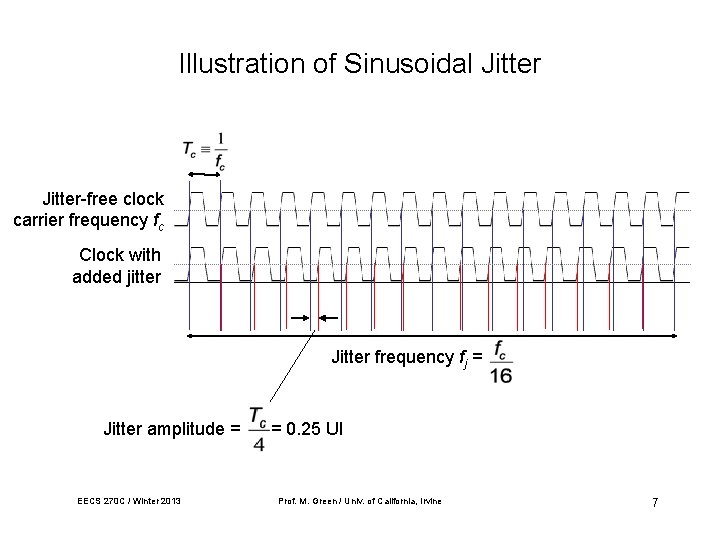
Illustration of Sinusoidal Jitter-free clock carrier frequency fc Clock with added jitter Jitter frequency fj = Jitter amplitude = EECS 270 C / Winter 2013 = 0. 25 UI Prof. M. Green / Univ. of California, Irvine 7

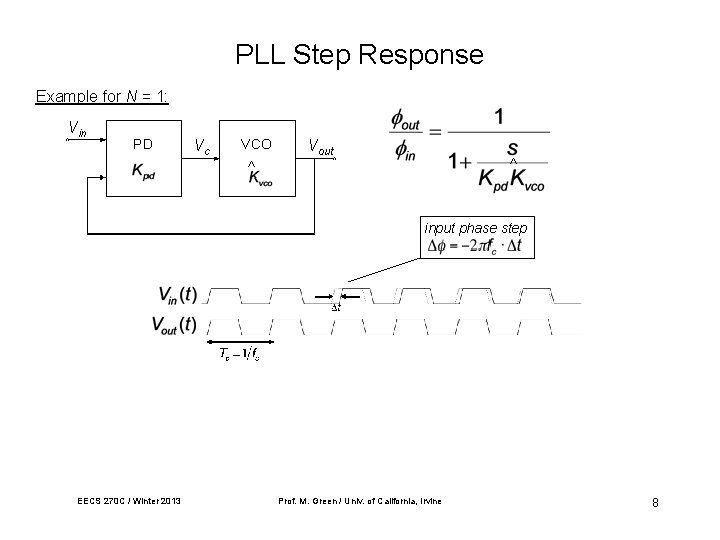
PLL Step Response Example for N = 1: Vin PD Vc VCO Vout ^ ^ input phase step 0 ^ ^ EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine ^ 8

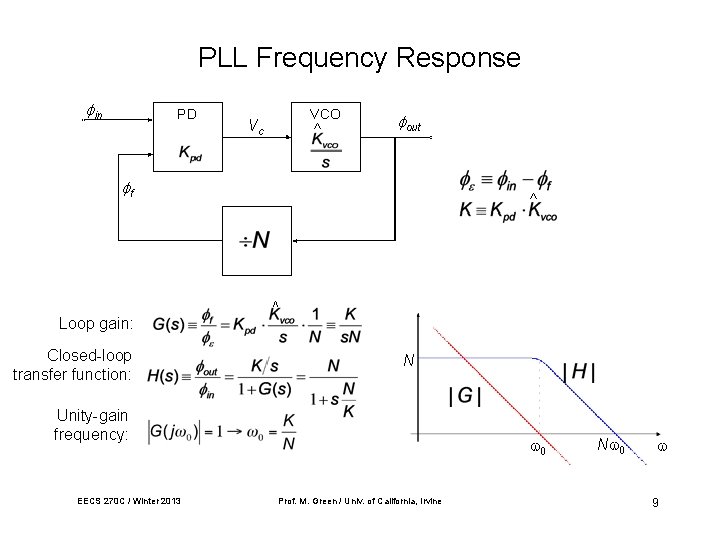
PLL Frequency Response in PD VCO Vc ^ out f ^ ^ Loop gain: Closed-loop transfer function: N Unity-gain frequency: EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine N 9

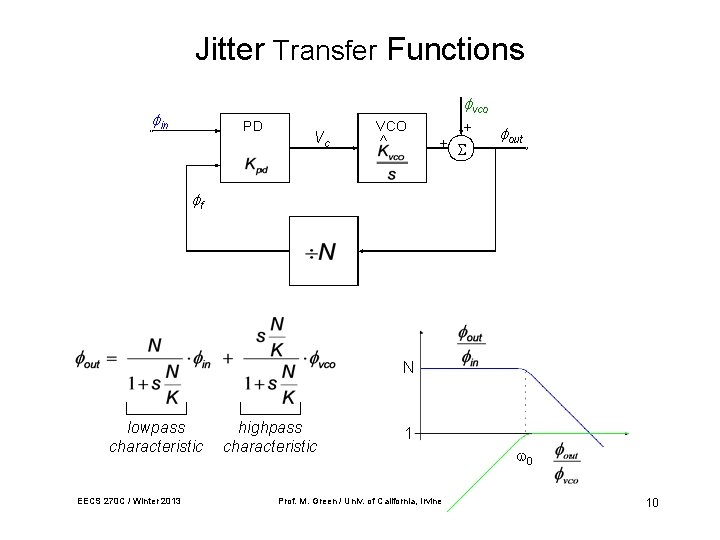
Jitter Transfer Functions vco in PD Vc VCO ^ + + out f N lowpass characteristic EECS 270 C / Winter 2013 highpass characteristic 1 Prof. M. Green / Univ. of California, Irvine 0 10

Disadvantages of 1 st-Order PLL • Higher-order transfer function would provide better attenuation of jitter. • Kpd & Kvco have circuit-related constraints; designer would prefer more degrees of freedom. • Phase detector operation requires filtering, which adds poles/zeros to the transfer function. EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 11

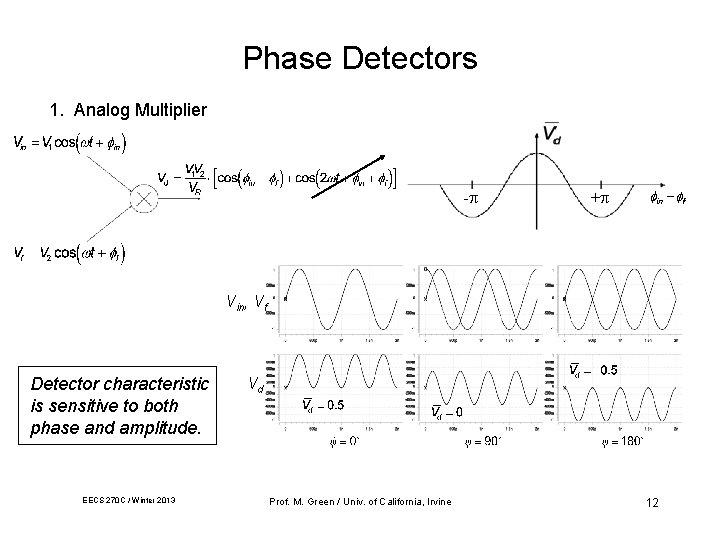
Phase Detectors 1. Analog Multiplier - + Vin, Vf Detector characteristic is sensitive to both phase and amplitude. EECS 270 C / Winter 2013 Vd Prof. M. Green / Univ. of California, Irvine 12

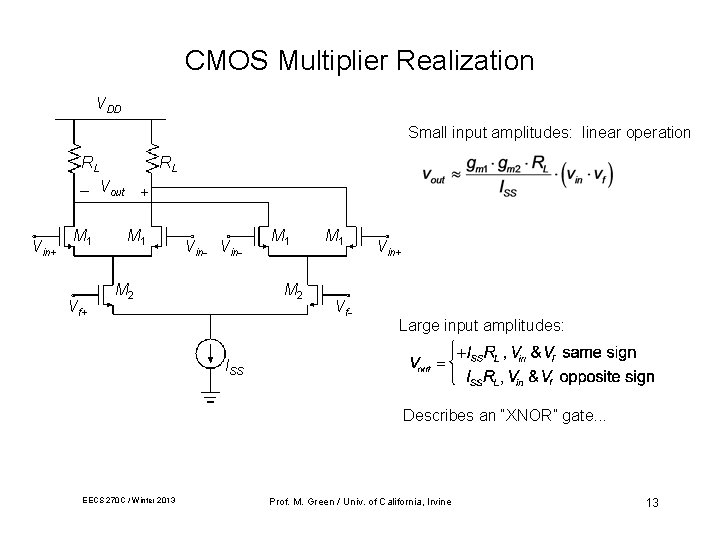
CMOS Multiplier Realization VDD Small input amplitudes: linear operation RL _ Vout Vin+ M 1 Vf+ RL + M 1 Vin- M 2 M 1 Vf- Vin+ Large input amplitudes: ISS Describes an “XNOR” gate. . . EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 13

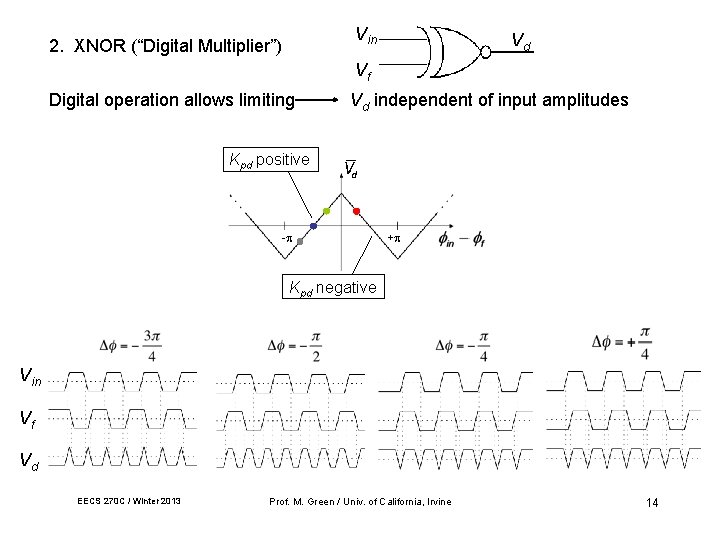
Vin 2. XNOR (“Digital Multiplier”) Vd Vf Digital operation allows limiting Vd independent of input amplitudes Kpd positive - + Kpd negative Vin Vf Vd EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 14

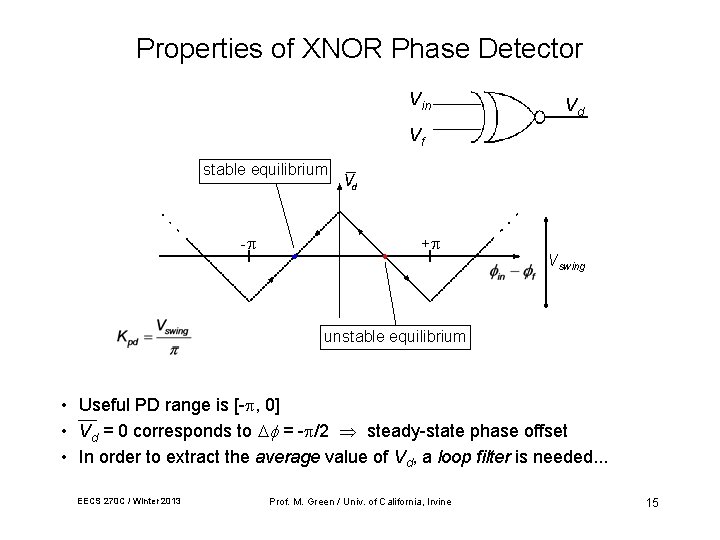
Properties of XNOR Phase Detector Vin Vd Vf stable equilibrium - + Vswing unstable equilibrium • Useful PD range is [- , 0] • Vd = 0 corresponds to = - /2 steady-state phase offset • In order to extract the average value of Vd, a loop filter is needed. . . EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 15

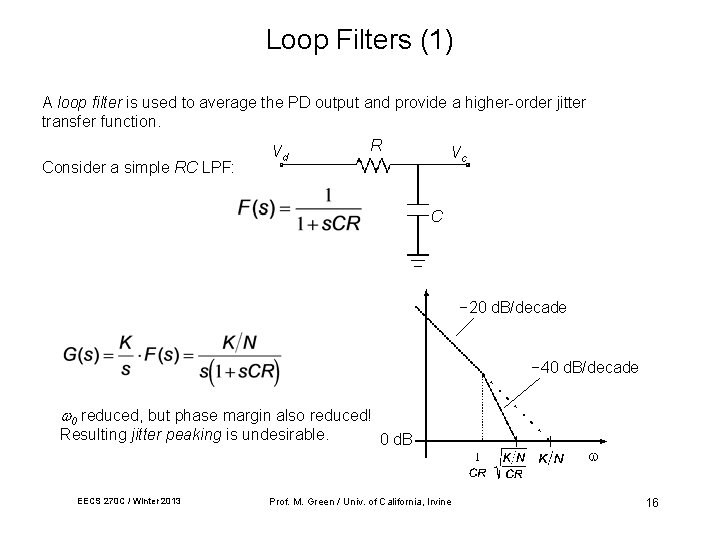
Loop Filters (1) A loop filter is used to average the PD output and provide a higher-order jitter transfer function. R Vd Vc Consider a simple RC LPF: C − 20 d. B/decade − 40 d. B/decade 0 reduced, but phase margin also reduced! Resulting jitter peaking is undesirable. EECS 270 C / Winter 2013 0 d. B Prof. M. Green / Univ. of California, Irvine 16

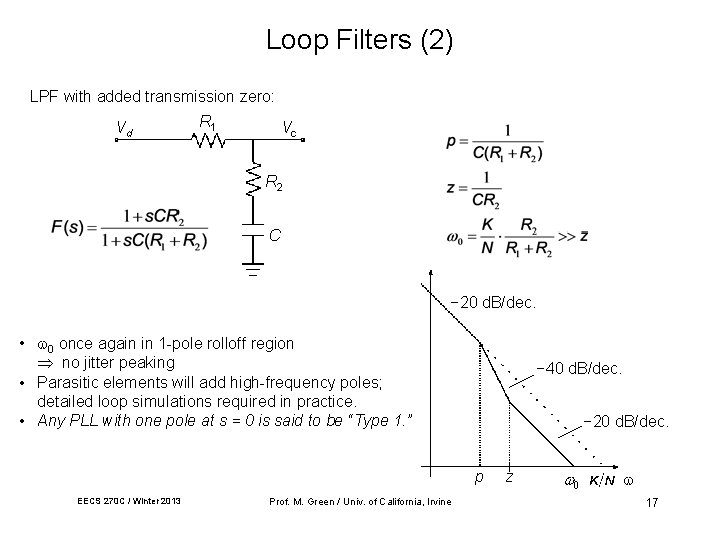
Loop Filters (2) LPF with added transmission zero: Vd R 1 Vc R 2 C − 20 d. B/dec. • 0 once again in 1 -pole rolloff region no jitter peaking • Parasitic elements will add high-frequency poles; detailed loop simulations required in practice. • Any PLL with one pole at s = 0 is said to be “Type 1. ” − 40 d. B/dec. − 20 d. B/dec. p EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine z 17

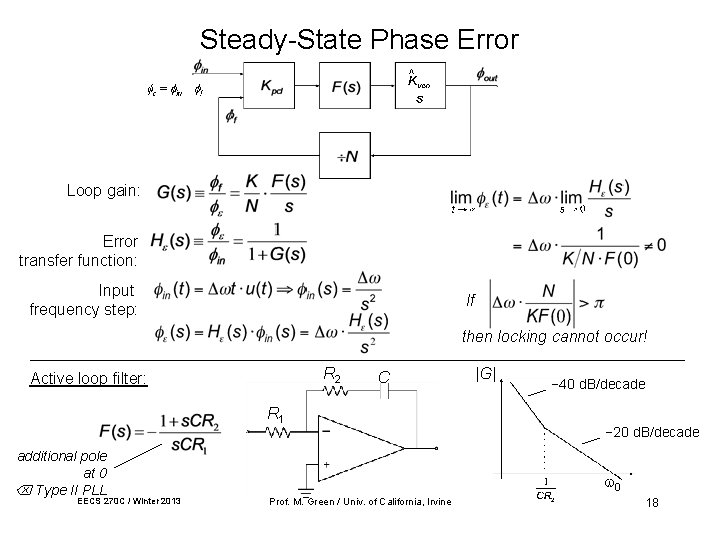
Steady-State Phase Error ^ Loop gain: Error transfer function: Input frequency step: If then locking cannot occur! R 2 Active loop filter: C R 1 additional pole at 0 Type II PLL EECS 270 C / Winter 2013 |G| − 40 d. B/decade − 20 d. B/decade 0 Prof. M. Green / Univ. of California, Irvine 18

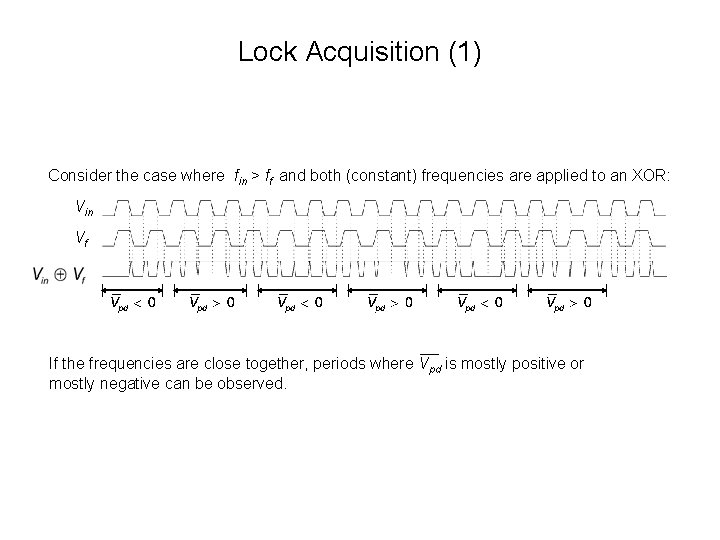
Lock Acquisition (1) Consider the case where fin > ff and both (constant) frequencies are applied to an XOR: Vin Vf If the frequencies are close together, periods where Vpd is mostly positive or mostly negative can be observed.

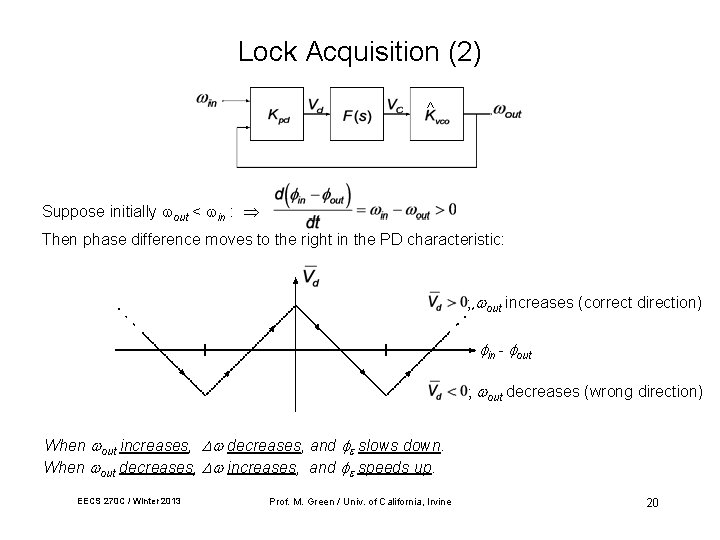
Lock Acquisition (2) ^ Suppose initially out < in : Then phase difference moves to the right in the PD characteristic: out increases (correct direction) in - out decreases (wrong direction) When out increases, decreases, and slows down. When out decreases, increases, and speeds up. EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 20

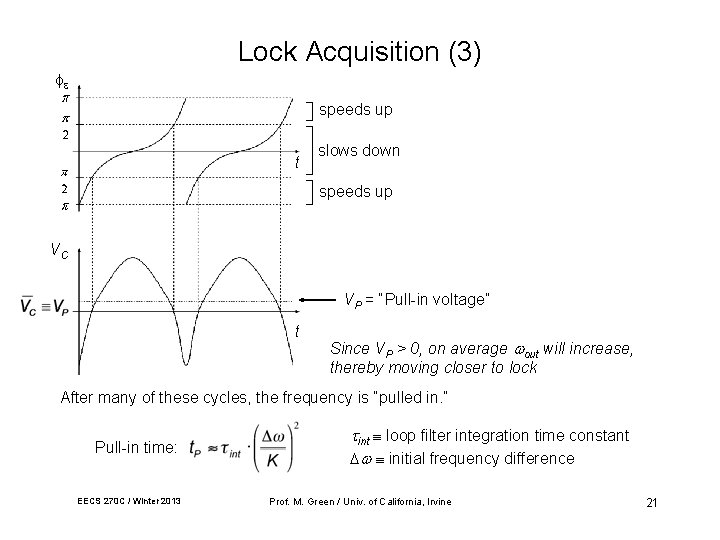
Lock Acquisition (3) speeds up t slows down speeds up VC VP = “Pull-in voltage” t Since VP > 0, on average out will increase, thereby moving closer to lock After many of these cycles, the frequency is “pulled in. ” Pull-in time: EECS 270 C / Winter 2013 int loop filter integration time constant initial frequency difference Prof. M. Green / Univ. of California, Irvine 21

Lock Acquisition (4) Control voltage transient showing pull-in: fin = 1 GHz Kvco = 5 MHz/V K = 106 rad/sec = 100 ns fout(0) = 1. 002 GHz cycle slips EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 22

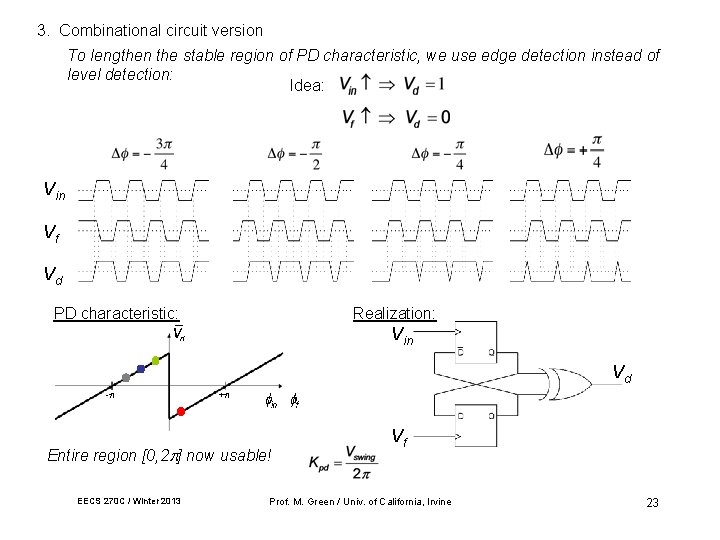
3. Combinational circuit version To lengthen the stable region of PD characteristic, we use edge detection instead of level detection: Idea: Vin Vf Vd PD characteristic: Realization: Vin Vd - + Entire region [0, 2 ] now usable! EECS 270 C / Winter 2013 Vf Prof. M. Green / Univ. of California, Irvine 23

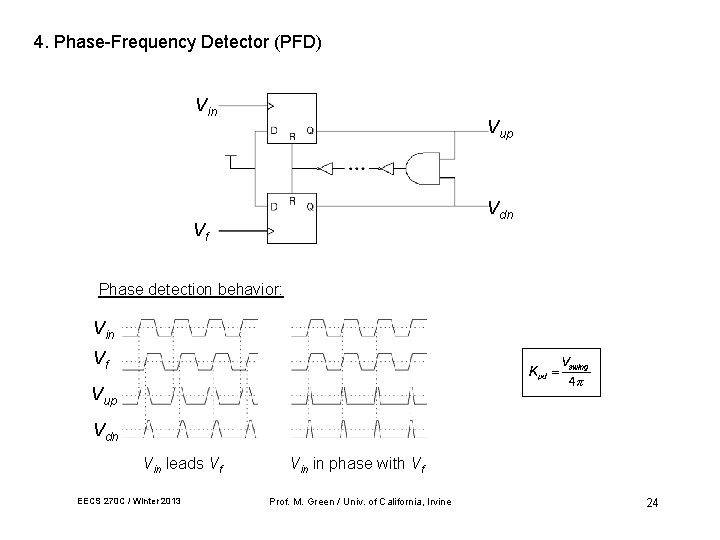
4. Phase-Frequency Detector (PFD) Vin Vup Vdn Vf Phase detection behavior: Vin Vf Vup Vdn Vin leads Vf EECS 270 C / Winter 2013 Vin in phase with Vf Prof. M. Green / Univ. of California, Irvine 24

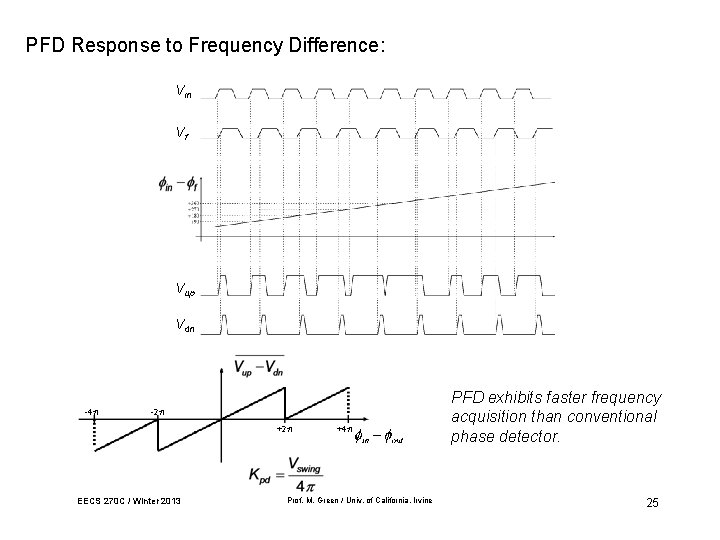
PFD Response to Frequency Difference: Vin Vf Vup Vdn -4 -2 +2 EECS 270 C / Winter 2013 +4 Prof. M. Green / Univ. of California, Irvine PFD exhibits faster frequency acquisition than conventional phase detector. 25

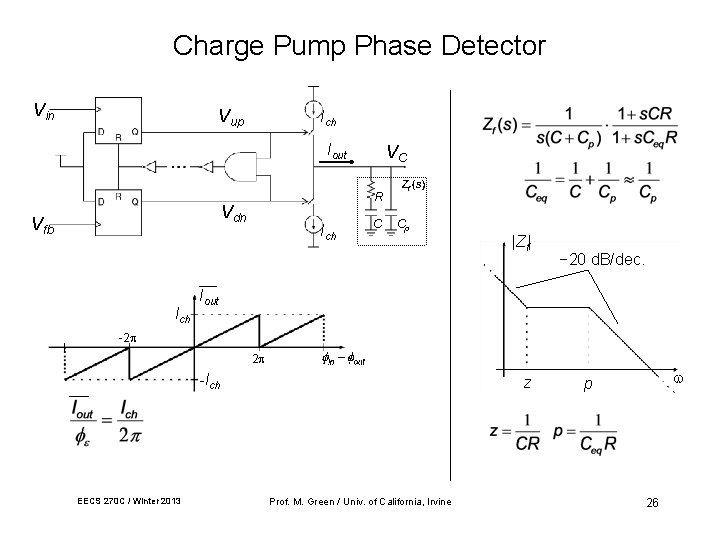
Charge Pump Phase Detector Vin Vup Ich Iout R Vdn Vfb Ich VC Ich C Cp |Zf| − 20 d. B/dec. Iout -2 2 -Ich EECS 270 C / Winter 2013 z Prof. M. Green / Univ. of California, Irvine p 26

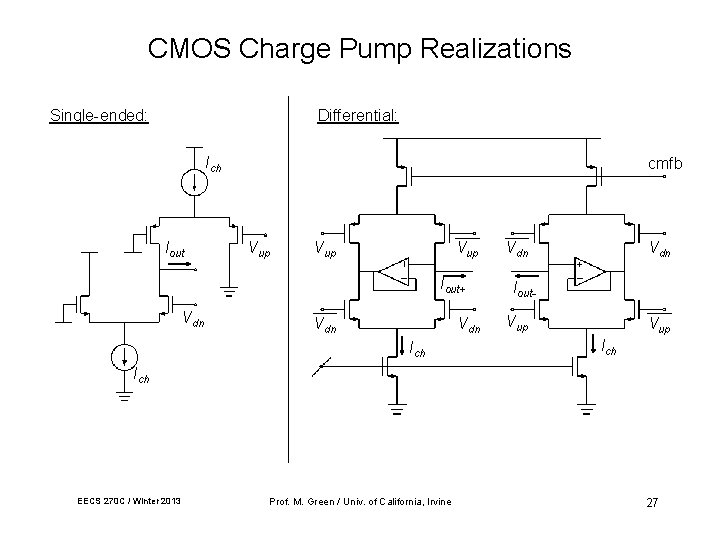
CMOS Charge Pump Realizations Single-ended: Differential: Ich Iout cmfb Vup Vup Iout+ Vdn Vdn Ich Vdn Iout. Vup Ich EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 27

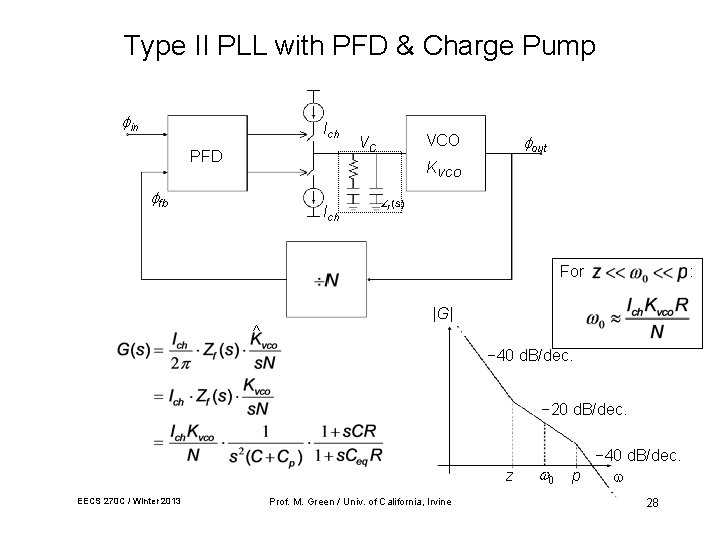
Type II PLL with PFD & Charge Pump in Ich PFD VC out VCO KVCO fb Ich For : |G| ^ − 40 d. B/dec. − 20 d. B/dec. z EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine − 40 d. B/dec. p 28

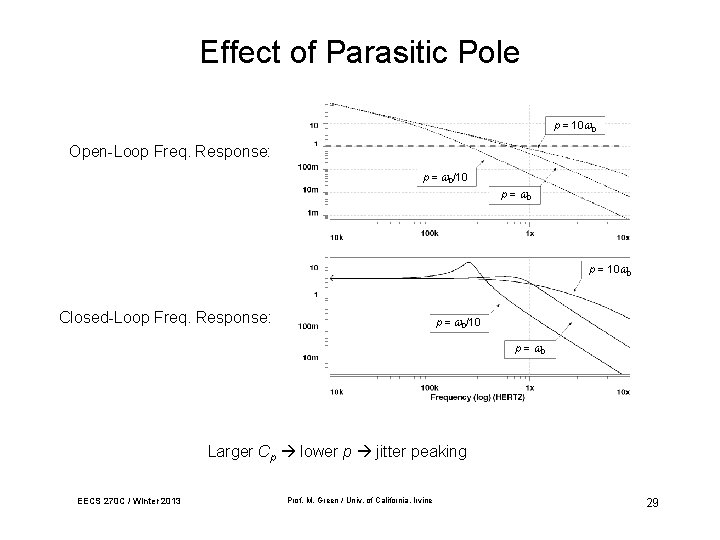
Effect of Parasitic Pole p = 10 0 Open-Loop Freq. Response: p = 0/10 p = 10 0 Closed-Loop Freq. Response: p = 0/10 p = 0 Larger Cp lower p jitter peaking EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 29

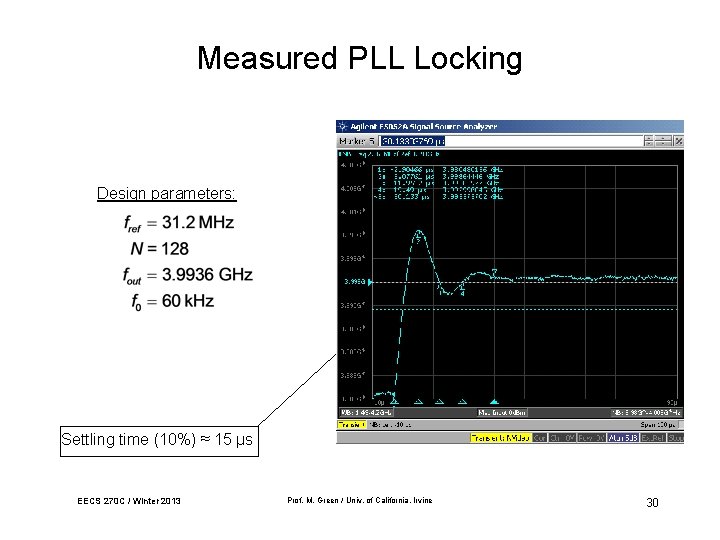
Measured PLL Locking Design parameters: Settling time (10%) ≈ 15 µs EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 30

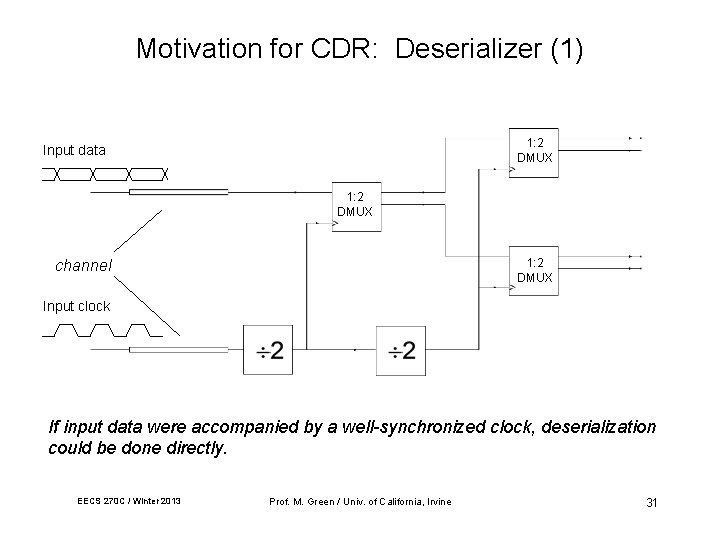
Motivation for CDR: Deserializer (1) 1: 2 DMUX Input data 1: 2 DMUX channel Input clock If input data were accompanied by a well-synchronized clock, deserialization could be done directly. EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 31

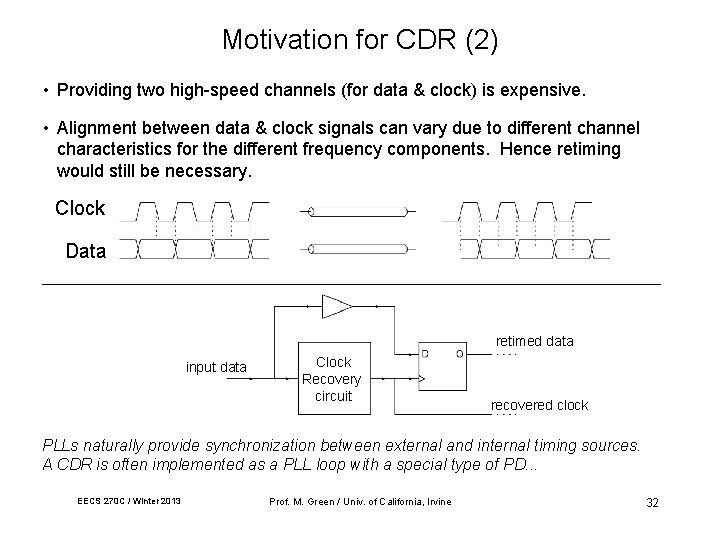
Motivation for CDR (2) • Providing two high-speed channels (for data & clock) is expensive. • Alignment between data & clock signals can vary due to different channel characteristics for the different frequency components. Hence retiming would still be necessary. Clock Data retimed data input data Clock Recovery circuit recovered clock PLLs naturally provide synchronization between external and internal timing sources. A CDR is often implemented as a PLL loop with a special type of PD. . . EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 32

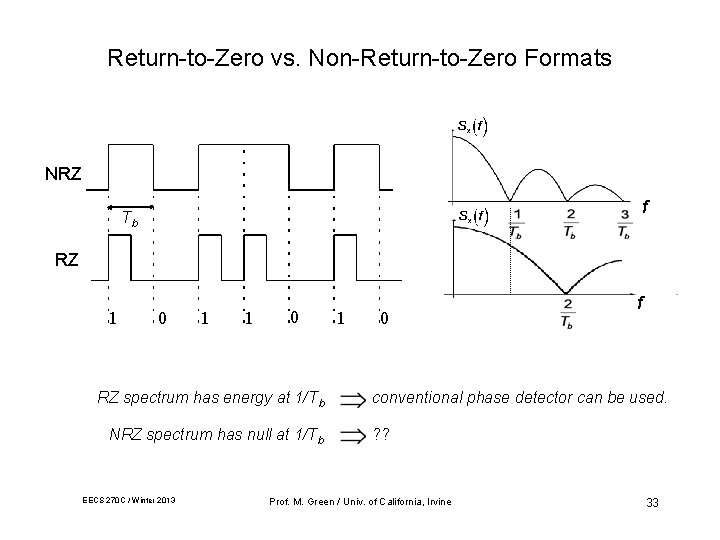
Return-to-Zero vs. Non-Return-to-Zero Formats NRZ f Tb RZ 1 0 1 1 0 RZ spectrum has energy at 1/Tb NRZ spectrum has null at 1/Tb EECS 270 C / Winter 2013 1 0 f conventional phase detector can be used. ? ? Prof. M. Green / Univ. of California, Irvine 33

Phase Detection of RZ Signals Vdata VRCK Vd • Phase detection operates same as for clock signals for logic 1. • Vd exhibits 50% duty cycle for logic 0. • Kpd will be data dependent. EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 34

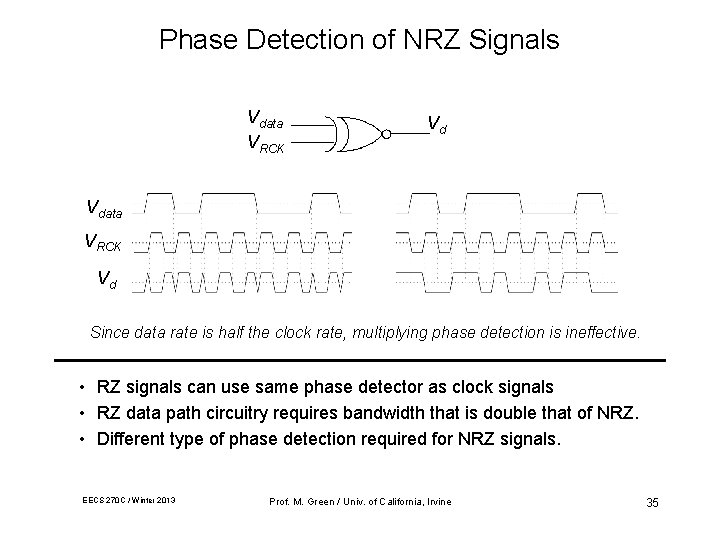
Phase Detection of NRZ Signals Vdata VRCK Vd Since data rate is half the clock rate, multiplying phase detection is ineffective. • RZ signals can use same phase detector as clock signals • RZ data path circuitry requires bandwidth that is double that of NRZ. • Different type of phase detection required for NRZ signals. EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 35

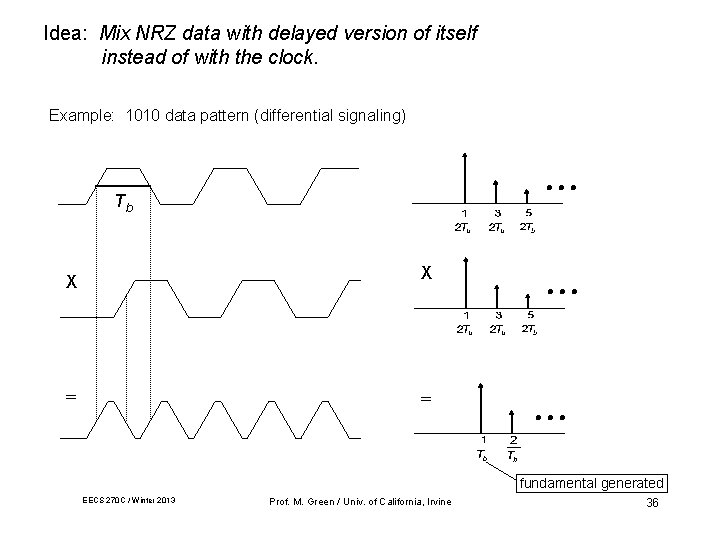
Idea: Mix NRZ data with delayed version of itself instead of with the clock. Example: 1010 data pattern (differential signaling) Tb X X = = fundamental generated EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 36

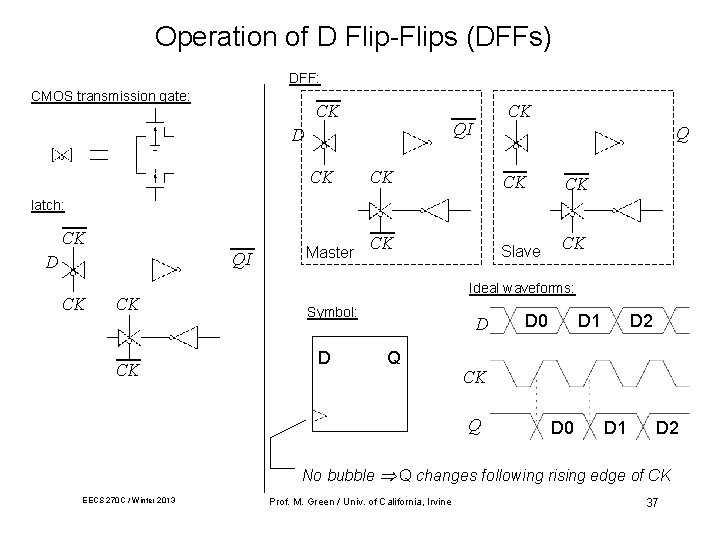
Operation of D Flip-Flips (DFFs) DFF: CMOS transmission gate: CK QI D CK CK Q CK CK Slave CK latch: CK QI D CK CK CK Master Ideal waveforms: Symbol: D D Q D 0 D 1 D 2 CK Q D 0 D 1 D 2 No bubble Q changes following rising edge of CK EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 37

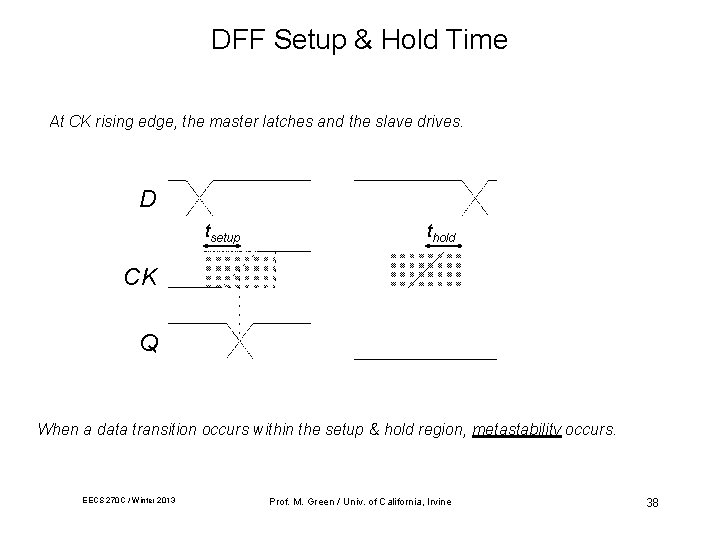
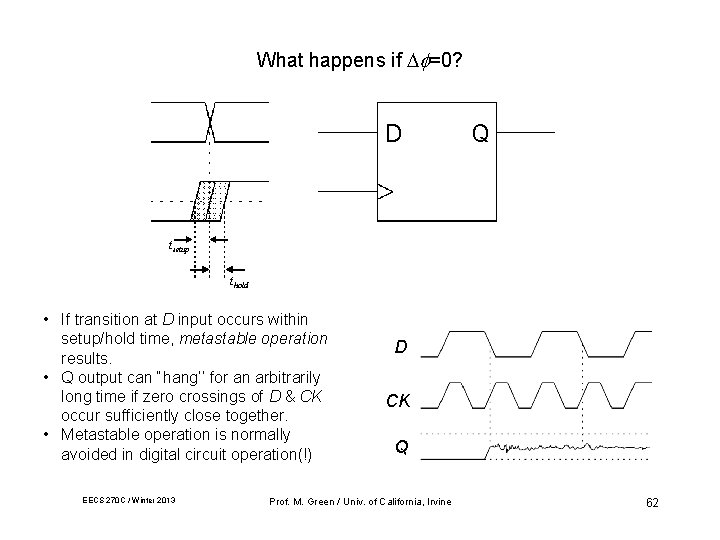
DFF Setup & Hold Time At CK rising edge, the master latches and the slave drives. D tsetup thold CK Q When a data transition occurs within the setup & hold region, metastability occurs. EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 38

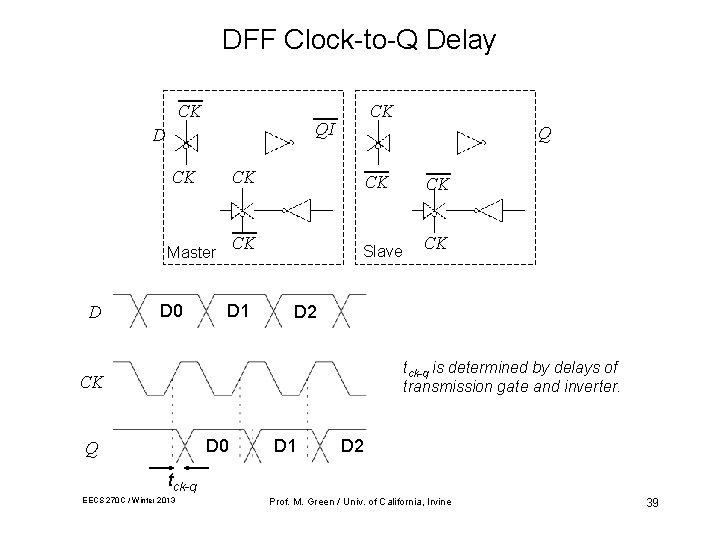
DFF Clock-to-Q Delay CK QI D CK Master D D 0 CK Q CK CK Slave CK D 1 D 2 tck-q is determined by delays of transmission gate and inverter. CK D 0 Q D 1 D 2 tck-q EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 39

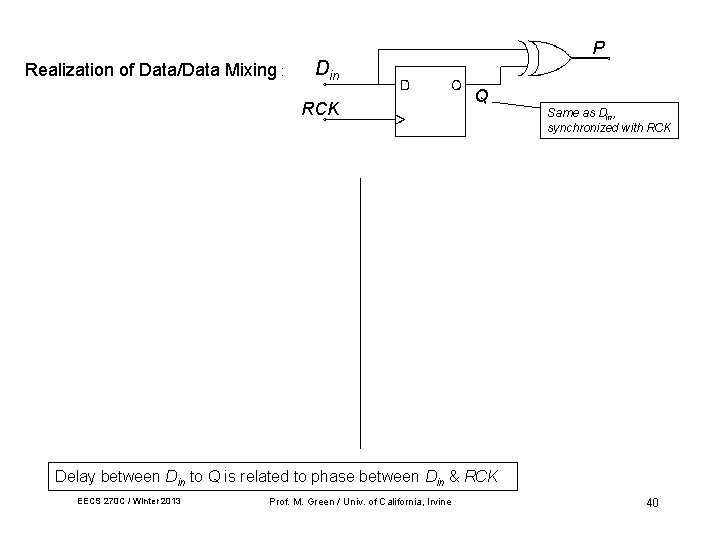
Realization of Data/Data Mixing : P Din Q RCK early: Din Same as Din, synchronized with RCK synchronized: D 1 D 0 D 2 D 0 D 3 D 1 D 2 D 3 RCK Q D 0 D 1 D 2 D 0 D 3 D 1 D 2 D 3 P D 0 D 1 D 2 D 3 D 4 Delay between Din to Q is related to phase between Din & RCK EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 40

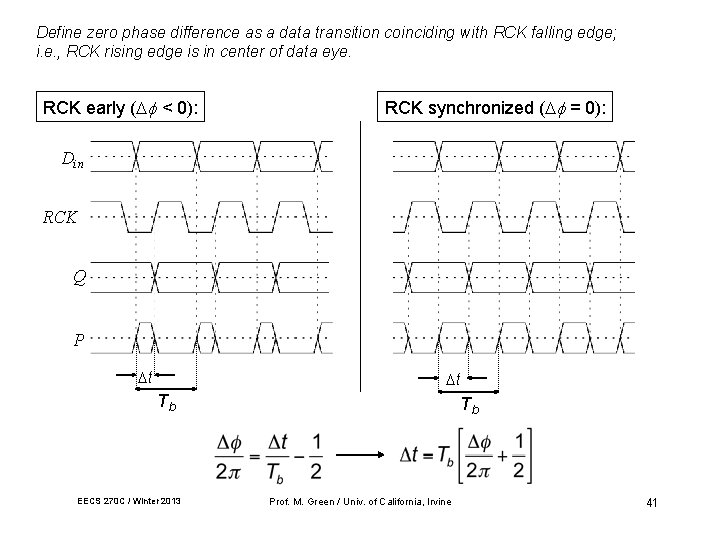
Define zero phase difference as a data transition coinciding with RCK falling edge; i. e. , RCK rising edge is in center of data eye. RCK early ( < 0): RCK synchronized ( = 0): Din RCK Q P t t Tb EECS 270 C / Winter 2013 Tb Prof. M. Green / Univ. of California, Irvine 41

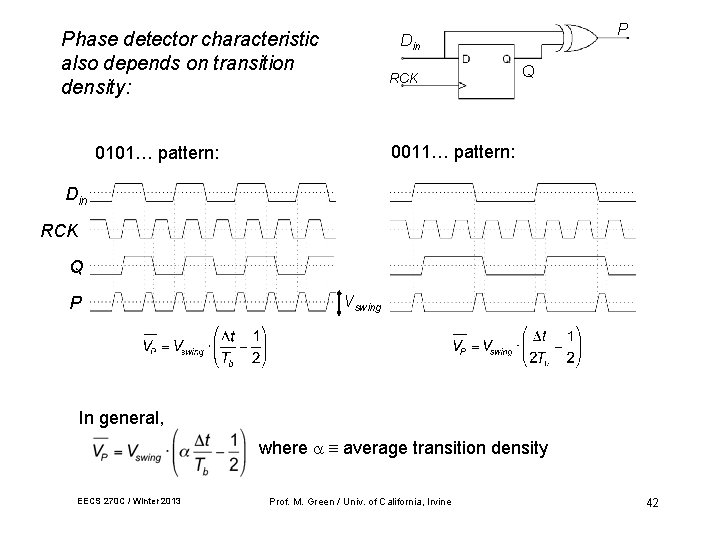
Phase detector characteristic also depends on transition density: P Din RCK Q 0011… pattern: 0101… pattern: Din RCK Q P Vswing In general, where average transition density EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 42

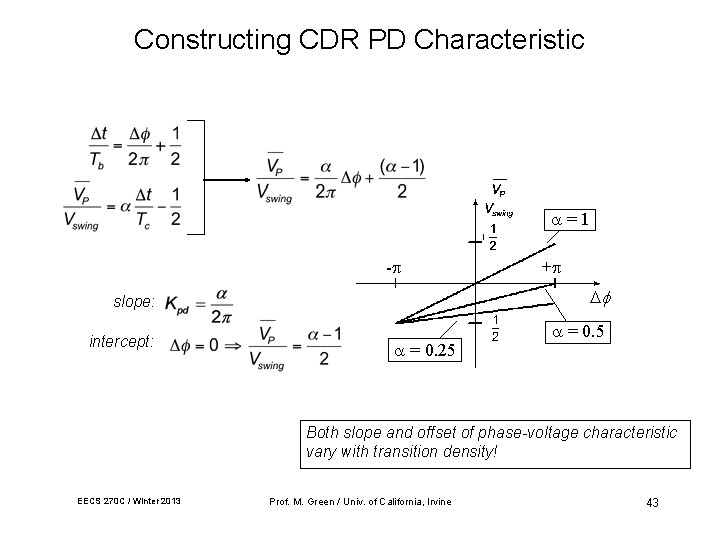
Constructing CDR PD Characteristic =1 - slope: intercept: + = 0. 25 = 0. 5 Both slope and offset of phase-voltage characteristic vary with transition density! EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 43

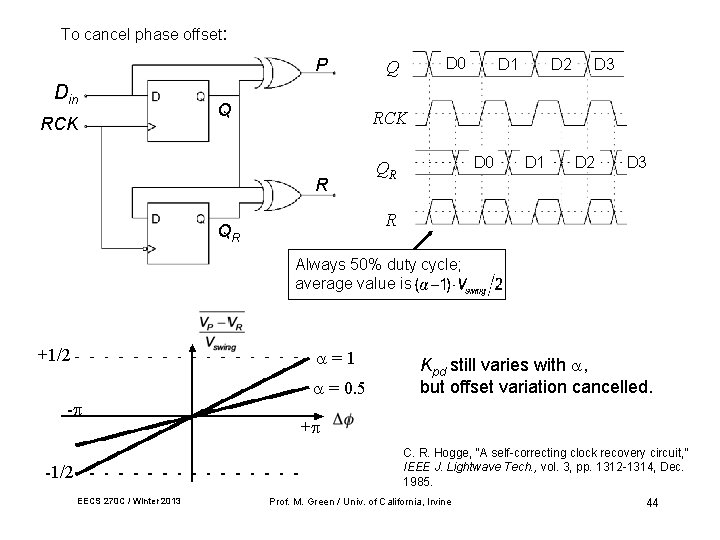
To cancel phase offset: P Din RCK Q D 0 Q D 1 D 2 D 3 RCK R D 0 QR D 1 D 2 D 3 R QR Always 50% duty cycle; average value is +1/2 =1 = 0. 5 - Kpd still varies with , but offset variation cancelled. + C. R. Hogge, “A self-correcting clock recovery circuit, ” IEEE J. Lightwave Tech. , vol. 3, pp. 1312 -1314, Dec. 1985. -1/2 EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 44

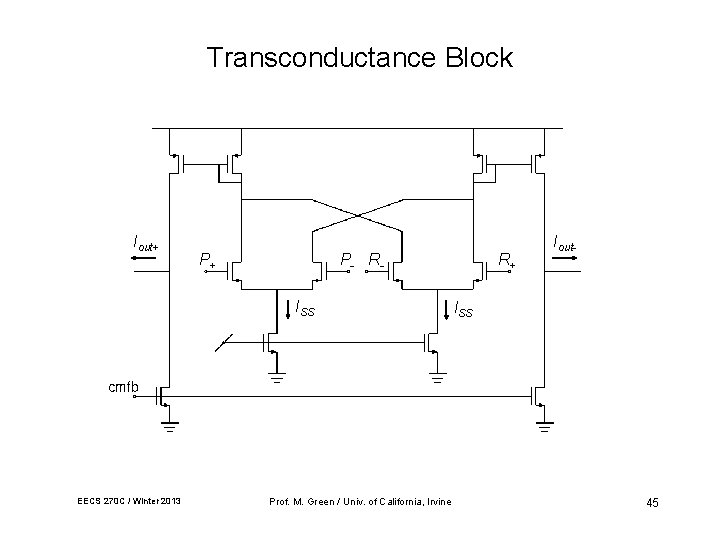
Transconductance Block Iout+ P+ P - RISS EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine R+ Iout- ISS 45

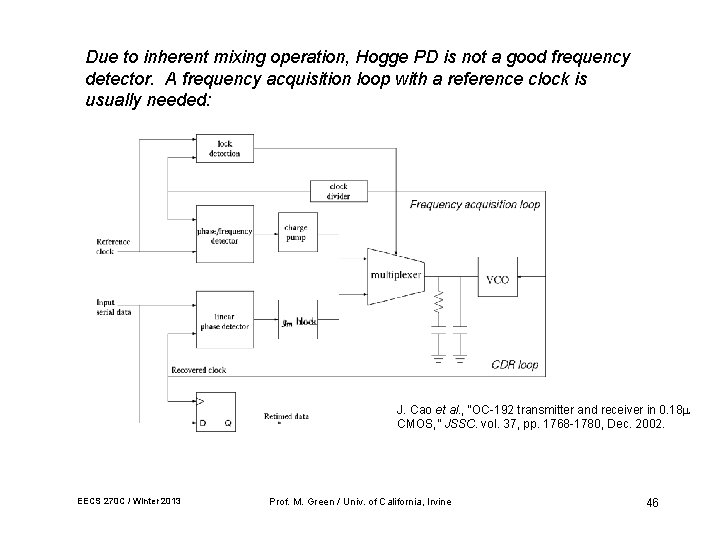
Due to inherent mixing operation, Hogge PD is not a good frequency detector. A frequency acquisition loop with a reference clock is usually needed: J. Cao et al. , “OC-192 transmitter and receiver in 0. 18 m CMOS, ” JSSC. vol. 37, pp. 1768 -1780, Dec. 2002. EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 46

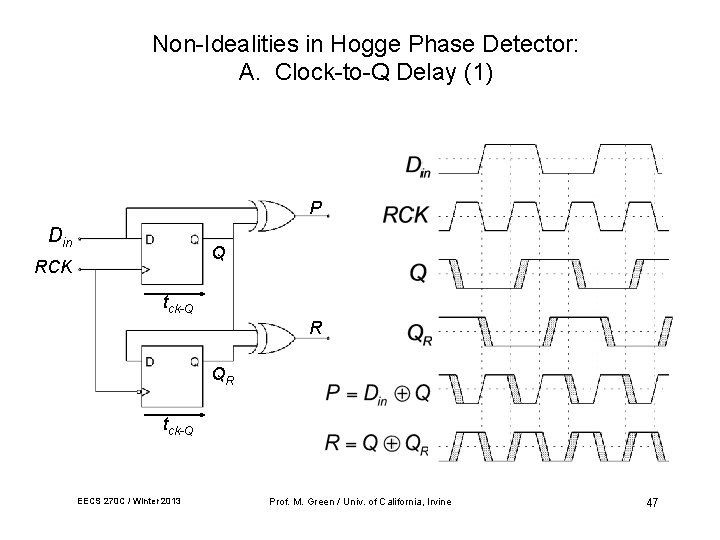
Non-Idealities in Hogge Phase Detector: A. Clock-to-Q Delay (1) P Din Q RCK tck-Q R QR tck-Q EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 47

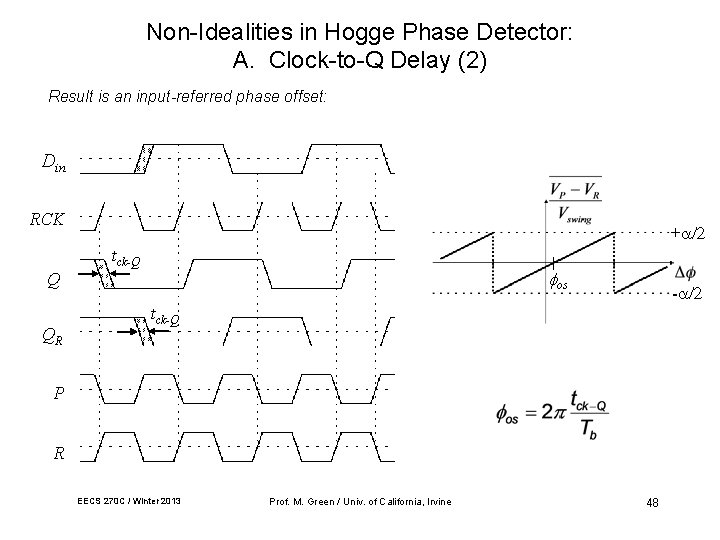
Non-Idealities in Hogge Phase Detector: A. Clock-to-Q Delay (2) Result is an input-referred phase offset: Din RCK + /2 tck-Q os Q QR - /2 tck-Q P R EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 48

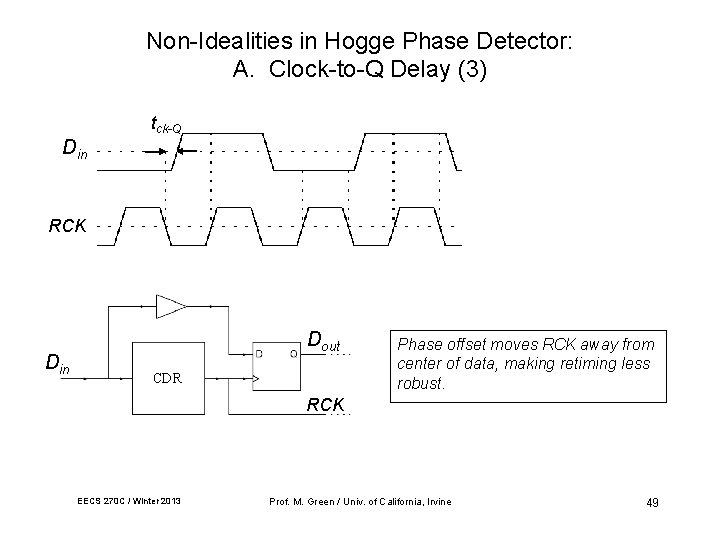
Non-Idealities in Hogge Phase Detector: A. Clock-to-Q Delay (3) tck-Q Din RCK Din Dout CDR Phase offset moves RCK away from center of data, making retiming less robust. RCK EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 49

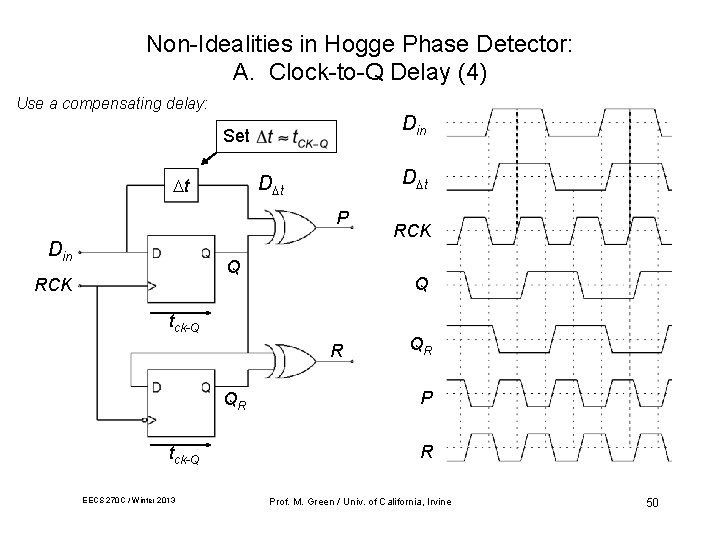
Non-Idealities in Hogge Phase Detector: A. Clock-to-Q Delay (4) Use a compensating delay: Din Set D t t P Din Q RCK Q tck-Q R QR tck-Q EECS 270 C / Winter 2013 RCK QR P R Prof. M. Green / Univ. of California, Irvine 50

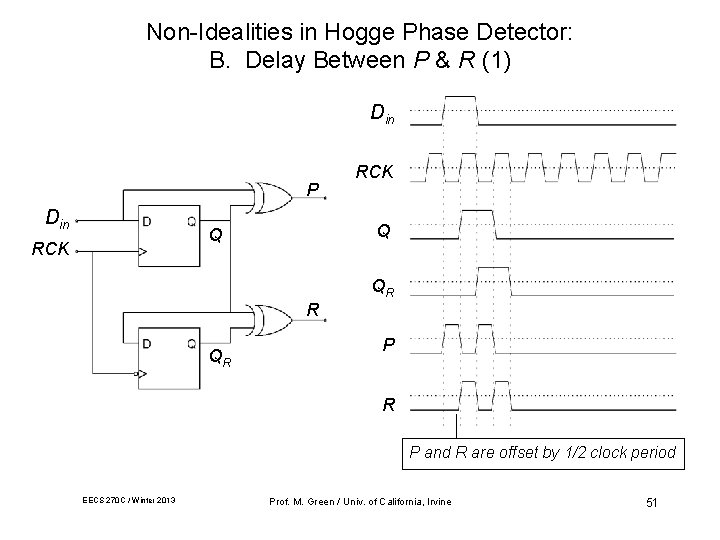
Non-Idealities in Hogge Phase Detector: B. Delay Between P & R (1) Din P Din Q Q RCK QR R QR P and R are offset by 1/2 clock period EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 51

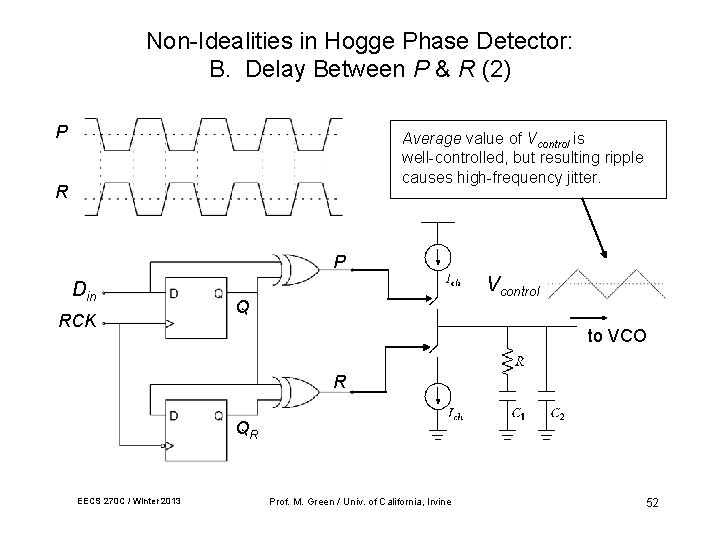
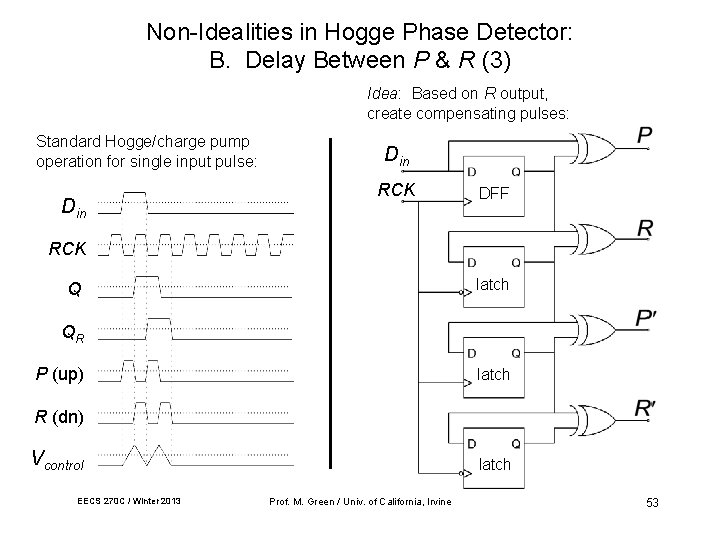
Non-Idealities in Hogge Phase Detector: B. Delay Between P & R (2) P Average value of Vcontrol is well-controlled, but resulting ripple causes high-frequency jitter. R P Din RCK Vcontrol Q to VCO R QR EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 52

Non-Idealities in Hogge Phase Detector: B. Delay Between P & R (3) Idea: Based on R output, create compensating pulses: Standard Hogge/charge pump operation for single input pulse: Din RCK DFF RCK latch Q QR P (up) latch R (dn) Vcontrol EECS 270 C / Winter 2013 latch Prof. M. Green / Univ. of California, Irvine 53

Non-Idealities in Hogge Phase Detector: B. Delay Between P & R (4) Din RCK DFF Q 1 Q 2 latch Q 2 Q 3 Q 4 P (up) latch Q 3 R (dn) P’(dn) latch Q 4 R’(up) Vcontrol Cancels out effect of next pulse EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 54

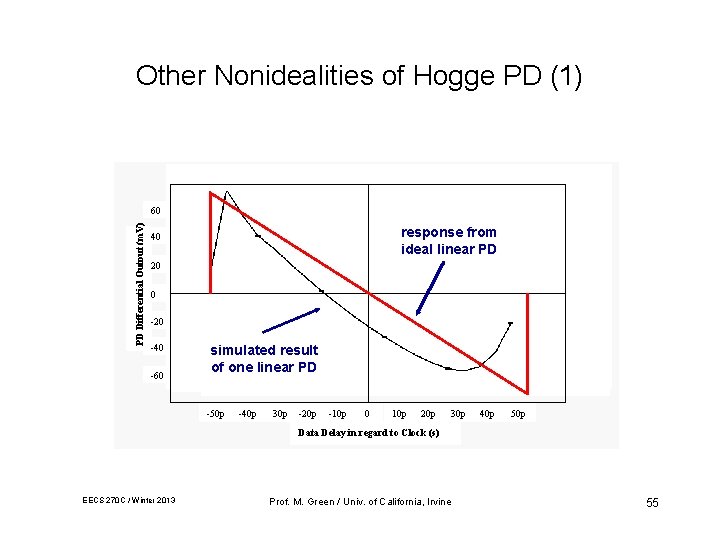
Other Nonidealities of Hogge PD (1) PD Differential Output (m. V) 60 response from ideal linear PD 40 20 0 -20 -40 -60 simulated result of one linear PD -50 p -40 p -30 p -20 p -10 p 0 10 p 20 p 30 p 40 p 50 p Data Delay in regard to Clock (s) EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 55

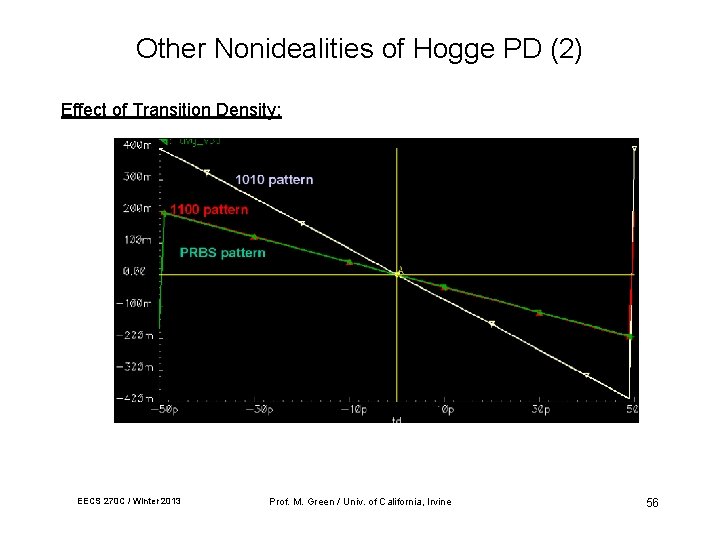
Other Nonidealities of Hogge PD (2) Effect of Transition Density: EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 56

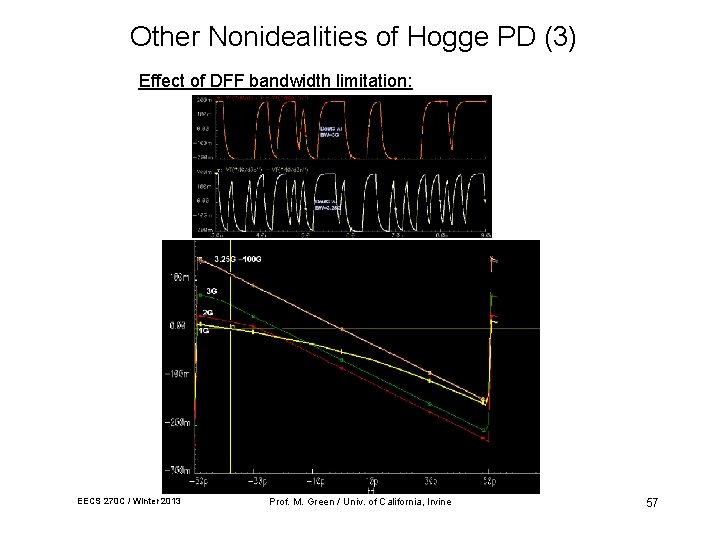
Other Nonidealities of Hogge PD (3) Effect of DFF bandwidth limitation: EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 57

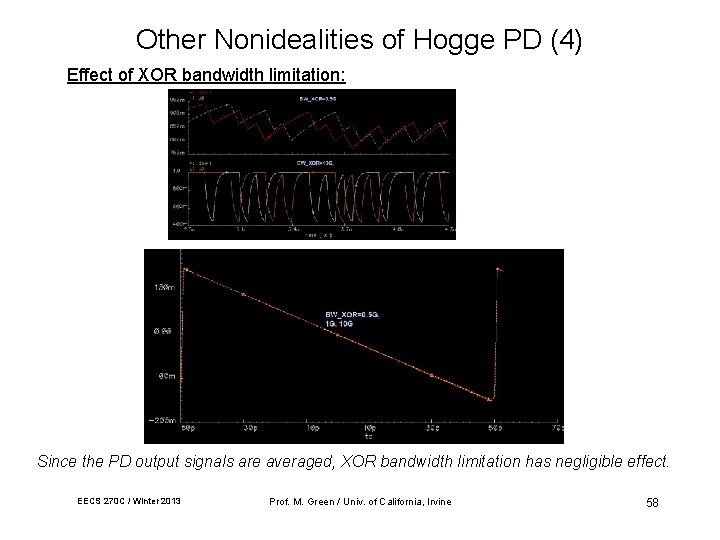
Other Nonidealities of Hogge PD (4) Effect of XOR bandwidth limitation: Since the PD output signals are averaged, XOR bandwidth limitation has negligible effect. EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 58

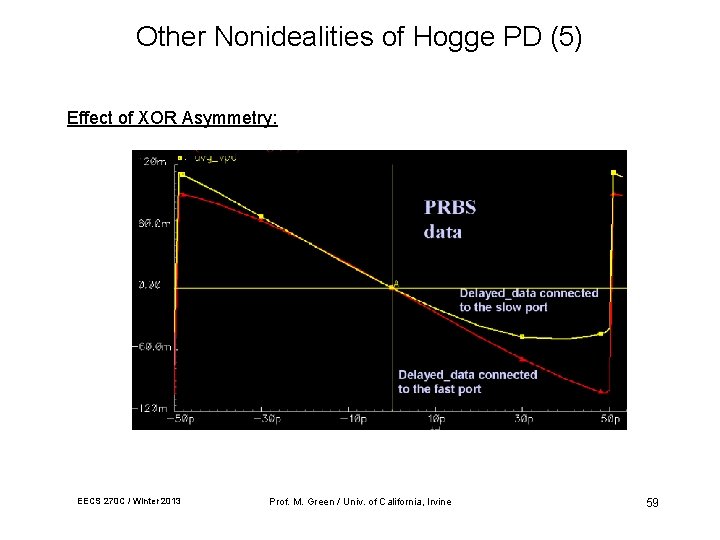
Other Nonidealities of Hogge PD (5) Effect of XOR Asymmetry: EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 59

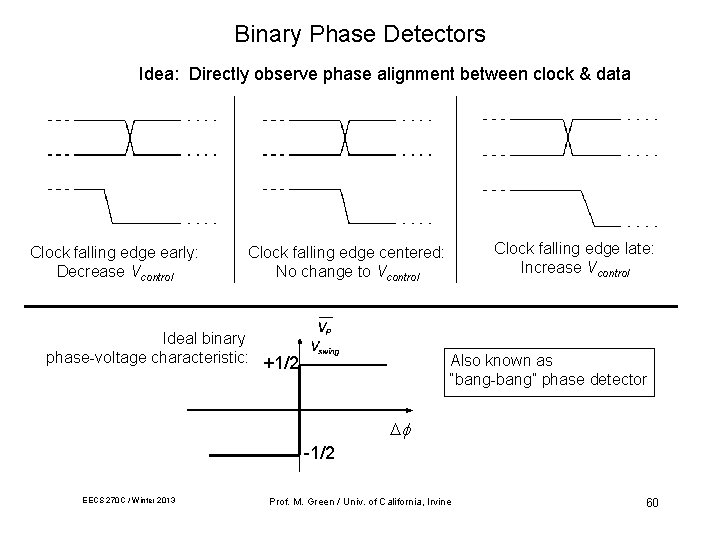
Binary Phase Detectors Idea: Directly observe phase alignment between clock & data Clock falling edge early: Decrease Vcontrol Clock falling edge late: Increase Vcontrol Clock falling edge centered: No change to Vcontrol Ideal binary phase-voltage characteristic: +1/2 Also known as “bang-bang” phase detector -1/2 EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 60

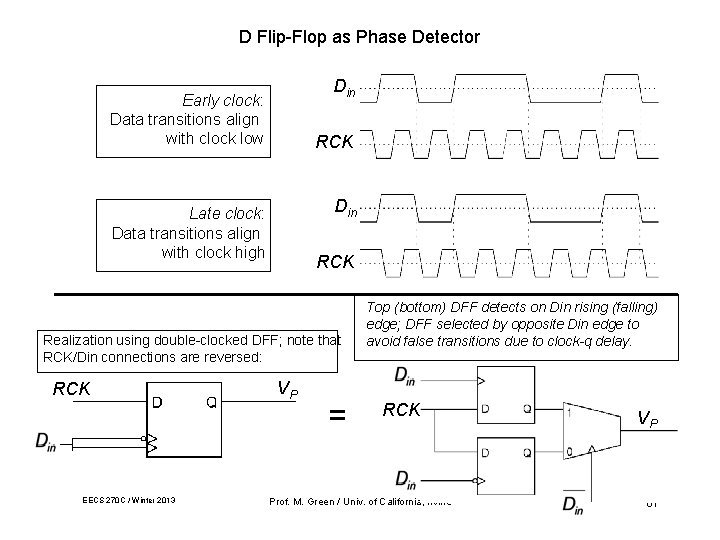
D Flip-Flop as Phase Detector Din Early clock: Data transitions align with clock low RCK Din Late clock: Data transitions align with clock high RCK Realization using double-clocked DFF; note that RCK/Din connections are reversed: RCK EECS 270 C / Winter 2013 VP = Top (bottom) DFF detects on Din rising (falling) edge; DFF selected by opposite Din edge to avoid false transitions due to clock-q delay. RCK Prof. M. Green / Univ. of California, Irvine VP 61

What happens if =0? tsetup thold • If transition at D input occurs within setup/hold time, metastable operation results. • Q output can “hang’’ for an arbitrarily long time if zero crossings of D & CK occur sufficiently close together. • Metastable operation is normally avoided in digital circuit operation(!) EECS 270 C / Winter 2013 D CK Q Prof. M. Green / Univ. of California, Irvine 62

Dog Dish Analogy ? ? ? A dog placed equidistant between two dog dishes will starve (in theory). EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 63

Non-Idealities in Binary DFF Phase Detector 1. Metastable operation difficult to characterize & simulate, varies widely over processing/temperature variations. Kpd (and therefore jitter transfer function parameters) are difficult to analyze. Exact value of Kpd depends on metastable behavior and varies with input jitter. 2. Large-amplitude pattern-dependent variation is present in phase detector output while locked. 3. During long runs phase detector output remains latched, resulting in VCO frequency changing continuously: RCK VP EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 64

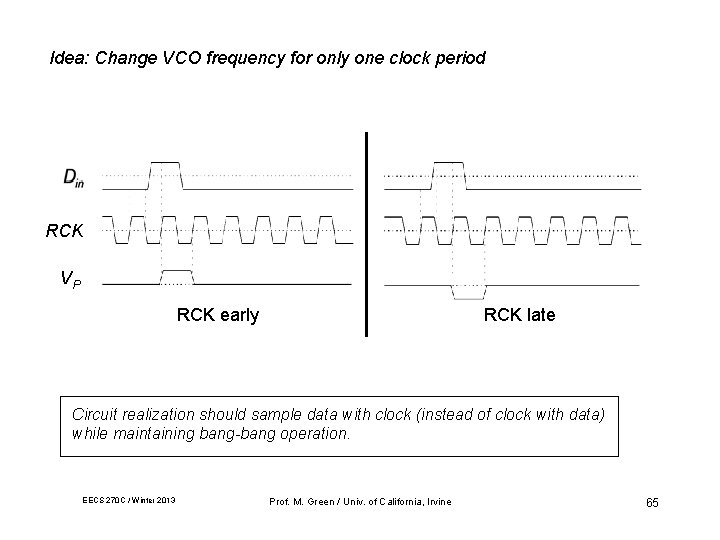
Idea: Change VCO frequency for only one clock period RCK VP RCK early RCK late Circuit realization should sample data with clock (instead of clock with data) while maintaining bang-bang operation. EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 65

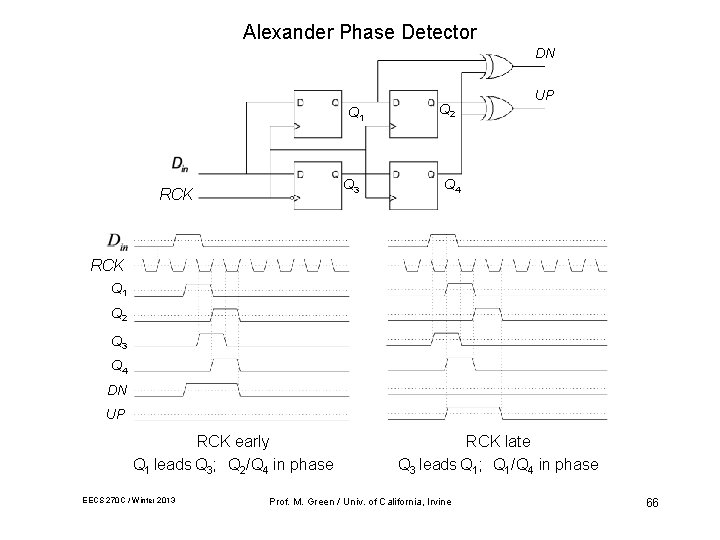
Alexander Phase Detector DN Q 1 Q 3 RCK Q 2 UP Q 4 RCK Q 1 Q 2 Q 3 Q 4 DN UP RCK early Q 1 leads Q 3; Q 2/Q 4 in phase EECS 270 C / Winter 2013 RCK late Q 3 leads Q 1; Q 1/Q 4 in phase Prof. M. Green / Univ. of California, Irvine 66

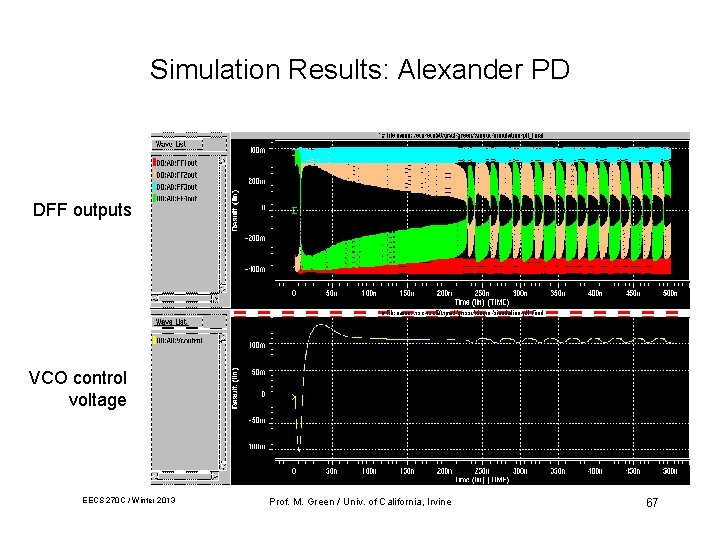
Simulation Results: Alexander PD DFF outputs VCO control voltage EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 67

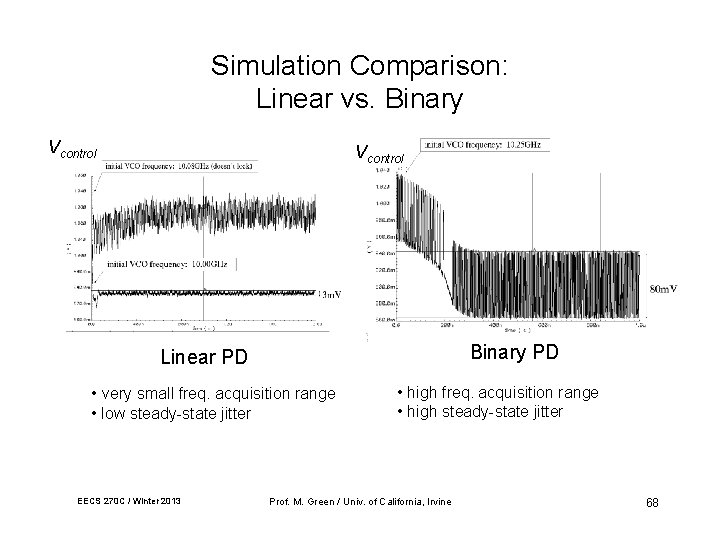
Simulation Comparison: Linear vs. Binary Vcontrol Binary PD Linear PD • very small freq. acquisition range • low steady-state jitter EECS 270 C / Winter 2013 • high freq. acquisition range • high steady-state jitter Prof. M. Green / Univ. of California, Irvine 68

Half-Rate CDRs To relax speed requirements for a given fabrication technology, a halfrate clock signal can be recovered: input data Din RCK full-rate recovered clock RCK 2 half-rate recovered clock • Can be used in in applications (e. g. , deserializer) where full-rate clock is not required. • Duty-cycle distortion will degrade bit-error ratio & jitter tolerance compared to full-rate versions. EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 69

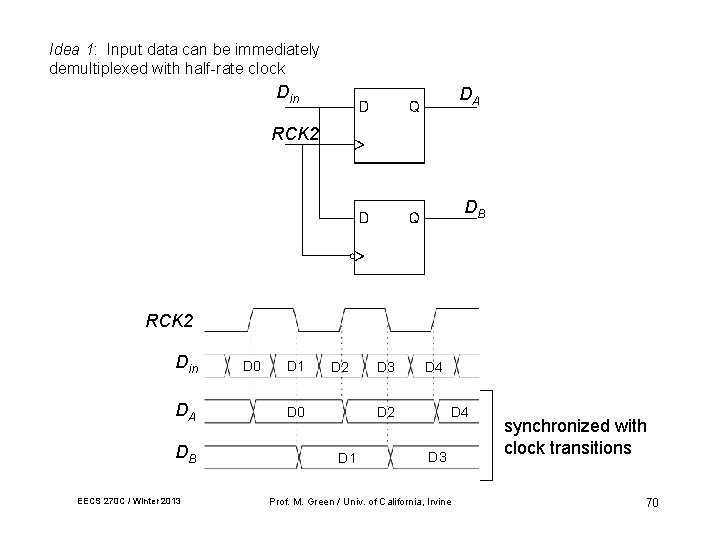
Idea 1: Input data can be immediately demultiplexed with half-rate clock Din DA RCK 2 DB RCK 2 Din DA DB EECS 270 C / Winter 2013 D 0 D 1 D 2 D 3 D 4 D 2 D 0 D 1 D 4 D 3 Prof. M. Green / Univ. of California, Irvine synchronized with clock transitions 70

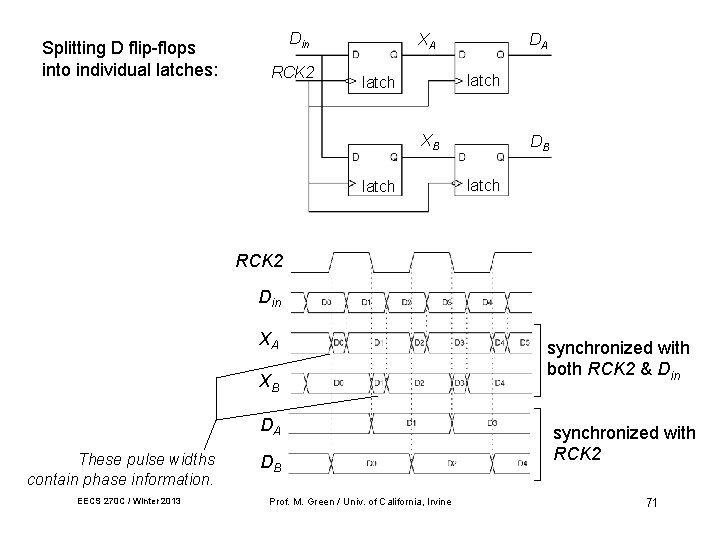
Splitting D flip-flops into individual latches: Din RCK 2 XA DA latch XB latch DB latch RCK 2 Din XA XB DA These pulse widths contain phase information. EECS 270 C / Winter 2013 DB Prof. M. Green / Univ. of California, Irvine synchronized with both RCK 2 & Din synchronized with RCK 2 71

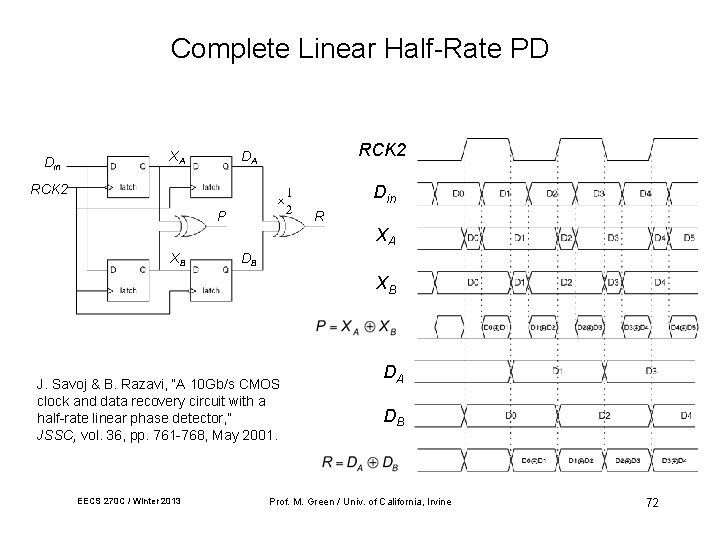
Complete Linear Half-Rate PD Din XA RCK 2 Din P R XA XB DB XB J. Savoj & B. Razavi, “A 10 Gb/s CMOS clock and data recovery circuit with a half-rate linear phase detector, ” JSSC, vol. 36, pp. 761 -768, May 2001. EECS 270 C / Winter 2013 DA DB Prof. M. Green / Univ. of California, Irvine 72

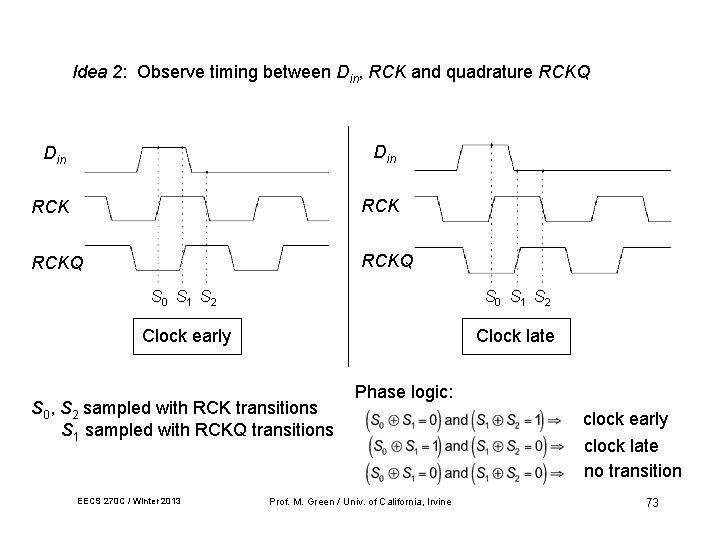
Idea 2: Observe timing between Din, RCK and quadrature RCKQ Din RCK RCKQ S 0 S 1 S 2 Clock early Clock late S 0, S 2 sampled with RCK transitions S 1 sampled with RCKQ transitions EECS 270 C / Winter 2013 Phase logic: Prof. M. Green / Univ. of California, Irvine clock early clock late no transition 73

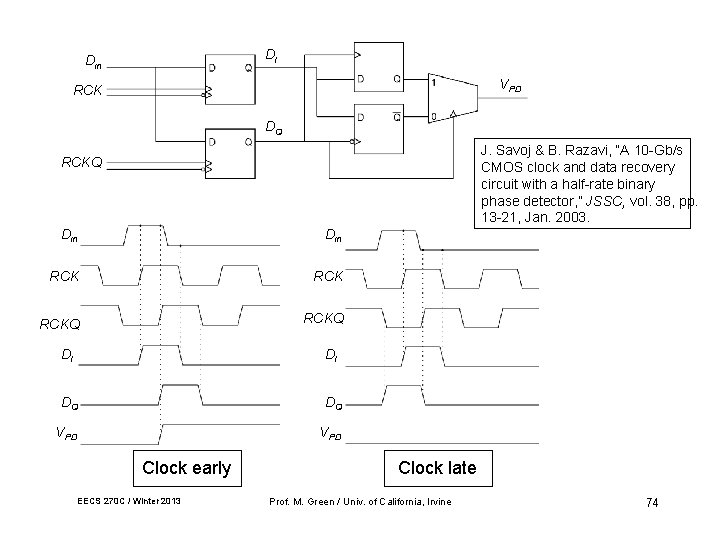
DI Din VPD RCK DQ J. Savoj & B. Razavi, “A 10 -Gb/s CMOS clock and data recovery circuit with a half-rate binary phase detector, ” JSSC, vol. 38, pp. 13 -21, Jan. 2003. RCKQ Din RCK RCKQ DI DI DQ DQ VPD Clock early EECS 270 C / Winter 2013 Clock late Prof. M. Green / Univ. of California, Irvine 74

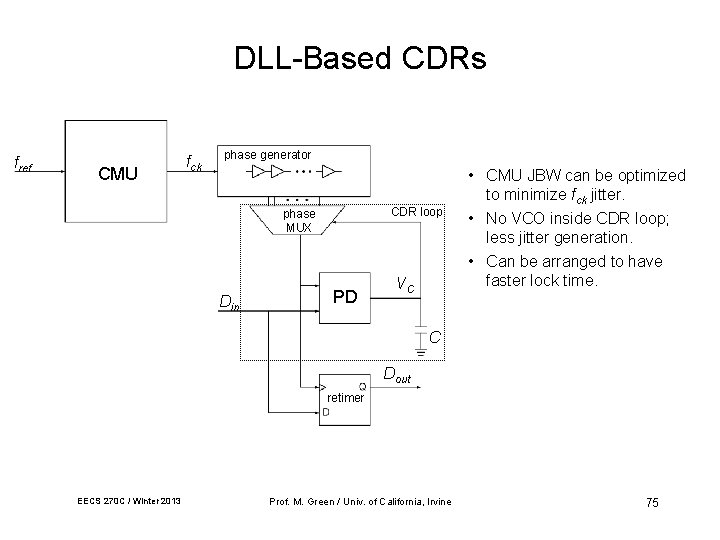
DLL-Based CDRs fref CMU fck phase generator CDR loop phase MUX Din PD VC • CMU JBW can be optimized to minimize fck jitter. • No VCO inside CDR loop; less jitter generation. • Can be arranged to have faster lock time. C Dout retimer EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine 75

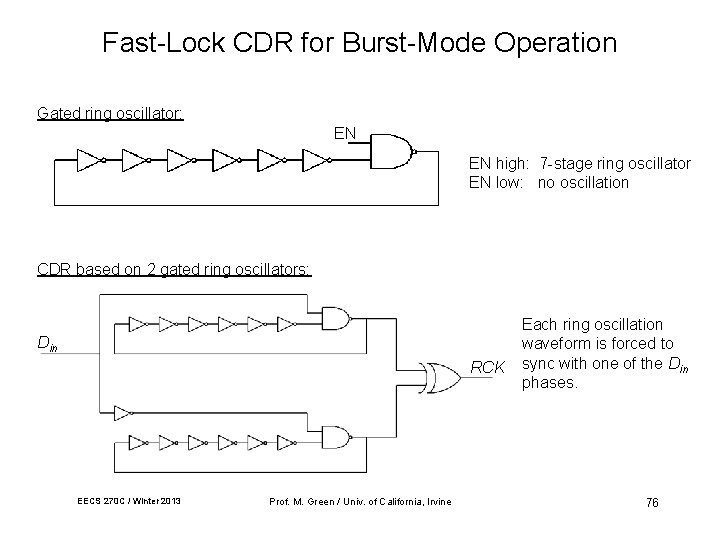
Fast-Lock CDR for Burst-Mode Operation Gated ring oscillator: EN EN high: 7 -stage ring oscillator EN low: no oscillation CDR based on 2 gated ring oscillators: Din RCK EECS 270 C / Winter 2013 Prof. M. Green / Univ. of California, Irvine Each ring oscillation waveform is forced to sync with one of the Din phases. 76