Synchronization in Networks of Coupled Harmonic Oscillators with

Synchronization in Networks of Coupled Harmonic Oscillators with Stochastic Perturbation and Time Delays 尚轶伦 上海交通大学 数学系

Outline Introduction ● Backgrounds ● Problem formulation Main result ● Synchronization of coupled harmonic oscillators Methods of proof Numerical examples

Synchronized oscillators Cellular clocks in the brain Pacemaker cells in the heart Pedestrians on a bridge Electric circuits Laser arrays Oscillating chemical reactions Bubbly fluids Neutrino oscillations Synchronous firings of male fireflies

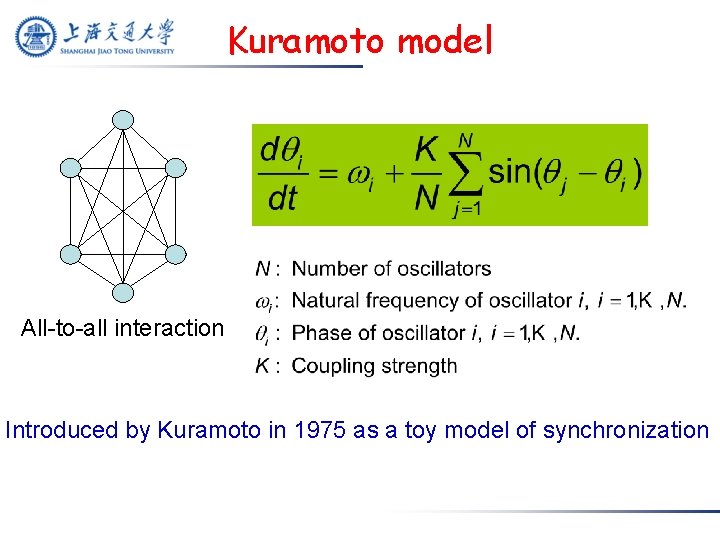
Kuramoto model All-to-all interaction Introduced by Kuramoto in 1975 as a toy model of synchronization

We want to study synchronization conditions for coupled harmonic oscillators over general directed topologies with noise perturbation and communication time delays.

Basic definitions For a matrix A, let ||A||=sup{ ||Ax||: ||x||=1}. || is the Euclidean norm. Let G=(V, E, A) be a weighted digraph with vertex set V={1, 2, . . . , n} and edge set E. An edge (j, i) ∈ E if and only if the agent j can send information to the agent i directly. The in-degree neighborhood of the agent i : Ni ={ j∈ V : (j, i) ∈ E}. A=(aij) ∈Rn×n is the weighted adjacency matrix of G. aij >0 if and only if j ∈ Ni. D=diag(d 1, . . . , dn) with di=|Ni|. The Laplacian matrix L=(lij) =D-A.

Our model Consider n coupled harmonic oscillators connected by dampers and each attached to fixed supports by identical springs with spring constant k. The dynamical system is described as xi’’+kxi+∑j∈Niaij(xi’-xj’)=0 for i=1, …, n where xi denotes the position of the ith oscillator, k is a positive gain, and aij characterizes interaction between oscillators i and j.

Here, we study a leader-follower version of the above system. Communication time delay and stochastic noises during the propagation of information from oscillator to oscillator are introduced. xi’’(t)+kxi(t)+∑j∈Niaij(xi’(t-s)-xj’(t-s))+bi(xi’(t-s)-x 0’(t-s))+ [∑j∈Nipij(xi’(t-s)-xj’(t-s))+qi(xi’(t-s)-x 0’(t-s))]wi’(t) = 0 for i=1, …, n x 0’’(t)+kx 0(t)=0, where s is the time delay and x 0 is the position of the virtual leader, labeled as oscillator 0. (1) (2)

Let B=diag(b 1, …, bn) be a diagonal matrix with nonnegative diagonal elements and bi>0 if and only if 0∈Ni. W(t): =(w 1(t), …, wn(t))T is an n dimensional standard Brownian motion. Let Ap=(pij) ∈Rn×n and Bp=diag(q 1, …, qn) be two matrices representing the intensity of noise. Let pi=∑jpij, Dp=diag(p 1, …, pn), and Lp=Dp-Ap.

Convergence analysis Let ri=xi and vi=xi’ for i=0, 1, …, n. Write r=(r 1, …, rn)T and v=(v 1, …, vn)T. Let r 0(t)=cos(√kt)r 0(0)+(1/k)sin(√kt)v 0(0) v 0(t)=-√ksin(√kt)r 0(0)+cos(√kt)v 0(0) Then r 0(t) and v 0(t) solve Equation (2)： x 0’’(t)+kx 0(t)=0

Let r*=r-r 01 and v*=v-v 01. we can obtain an error dynamics of (1) and (2) as follows dz(t)=[Ez(t)+Fz(t-s)]dt+Hz(t-s)d. W(t) where, z= (r*, v*)T, E= 0 In -k. In 0 , 0 0 F= 0 -L-B 0 0 , H= 0 -Lp-Bp and W(t) is an 2 n dimensional standard Brownian motion.

The theorem Theorem: Suppose that vertex 0 is globally reachable in G. If ||H||2||P||+2||PF||√ {8 s 2[(k∨ 1)2+||F||2]+2 s||H||2} <Eigenvaluemin(Q), where P and Q are two symmetric positive definite matrices such that P(E+F)+(E+F)TP=-Q, then by using algorithms (1) and (2), we have r(t)-r 0(t)1→ 0, v(t)-v 0(t)1→ 0 almost surely, as t→∞.

Method of proof Consider an n dimensional stochastic differential delay equation dx(t)=[Ex(t)+Fx(t-s)]dt+g(t, x(t), x(t-s))d. W(t) (3) where E and F are n×n matrices, g : [0, ∞) ×Rn×Rn→Rn×m is locally Lipschitz continuous and satisfies the linear growth condition with g(t, 0, 0) ≡ 0. W(t) is an m dimensional standard Brownian motion.

Lemma (X. Mao): Assume that there exists a pair of symmetric positive definite n×n matrices P and Q such that P(E+F)+(E+F) TP=-Q. Assume also that there exist non-negative constants a and b such that Trace[g. T(t, x, y)g(t, x, y)] ≤a||x||2+b||y||2 for all (t, x, y). If (a+b)||P||+2||PF||√{2 s(4 s(||E||2+||F||2)+a+b)} <Eigenvalue min(Q), then the trivial solution of Equation (3) is almost surely exponentially stable.

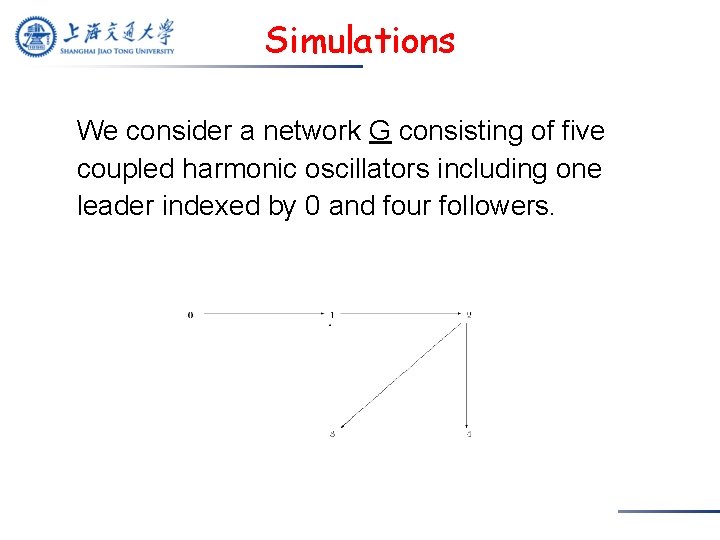
Simulations We consider a network G consisting of five coupled harmonic oscillators including one leader indexed by 0 and four followers.

Let aij=1 if j∈Ni and aij=0 otherwise; bi=1 if 0∈Ni and bi=0 otherwise. Take the noise intensity matrices Lp=0. 1 L and Bp=0. 1 B. Take Q=I 8 with Eigenvaluemin(Q)=1. Calculate to get ||H||=0. 2466 and ||F||=2. 4656. In what follows, we will consider two different gains k.

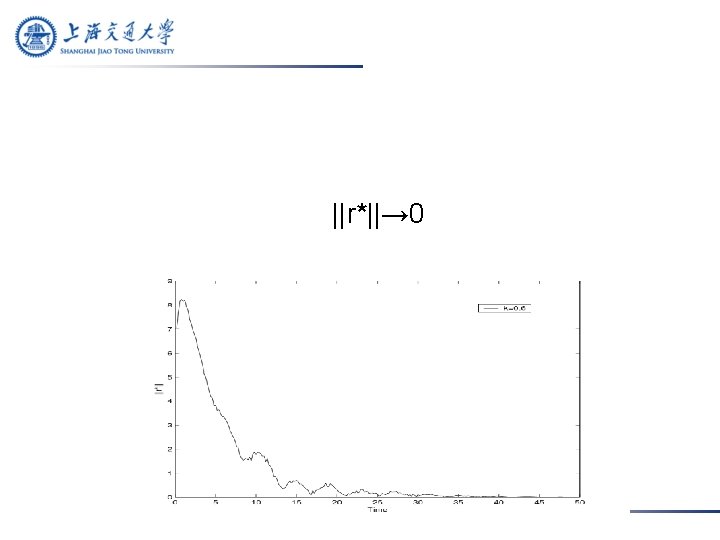
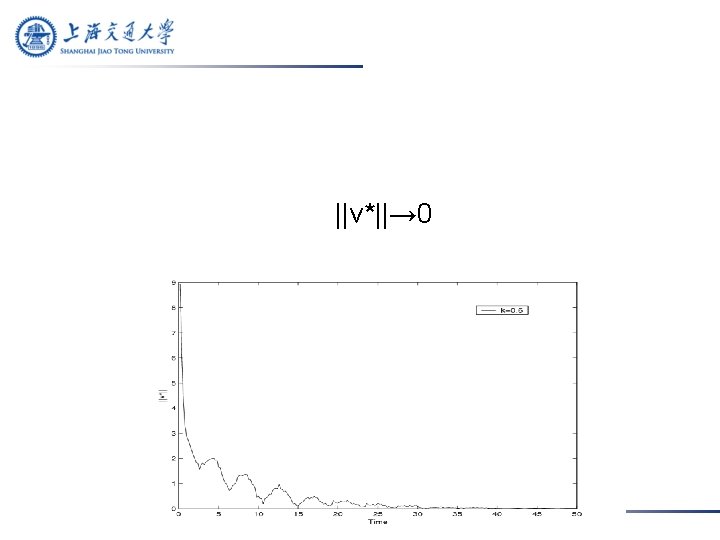
Firstly, take k=0. 6 such that ||E||=1>k. We solve P from the equation P(E+F)+(E+F)TP=-Q and get ||P||=8. 0944 and ||PF||=4. 1688. Conditions in the Theorem are satisfied by taking time delay s=0. 002. Take initial value z(0)=(-5, 1, 4, -3, -8, 2, -1. 5, 3)T.

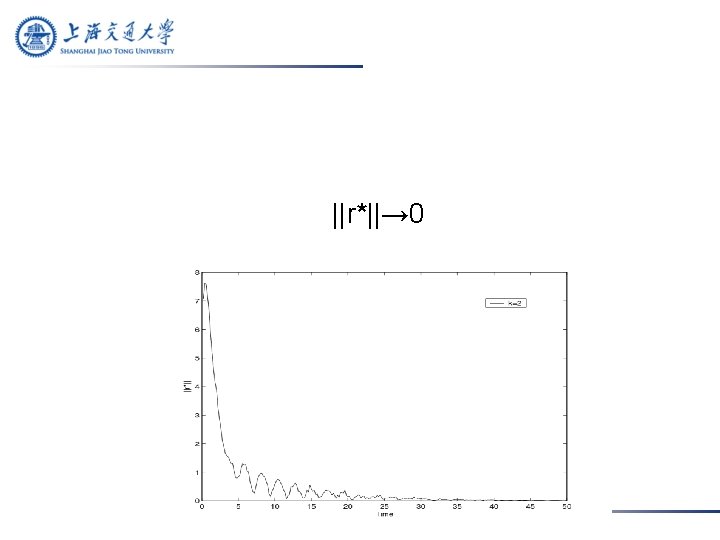
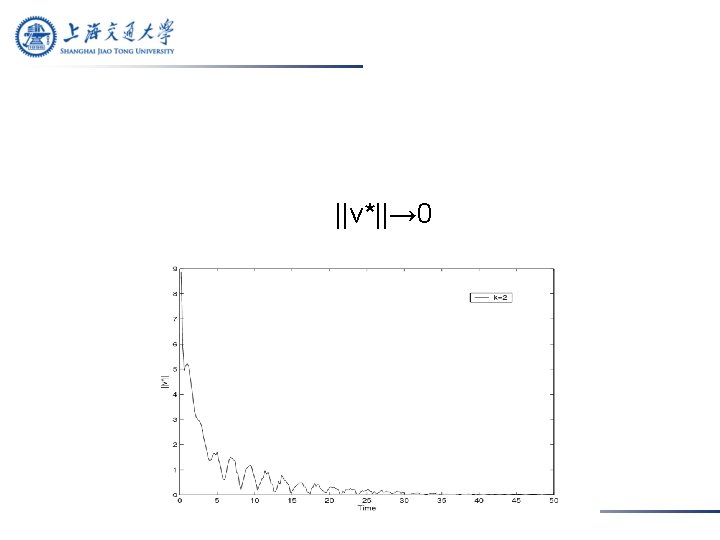
Secondly, take k=2 such that ||E||=k>1. In this case, we get ||P||=8. 3720 and ||PF||=7. 5996. Conditions in the Theorem are satisfied by taking time delay s=0. 001. Take the same initial value z(0).

The value of k not only has an effect on the magnitude and frequency of the synchronized states (as implied in the Theorem), but also affects the shapes of synchronization error curves ||r*|| and ||v*||.

Thanks for your Attent ion! Email: shyl@sjtu. edu. cn