Synaptic integration cable theory Isopotential sphere Current injected

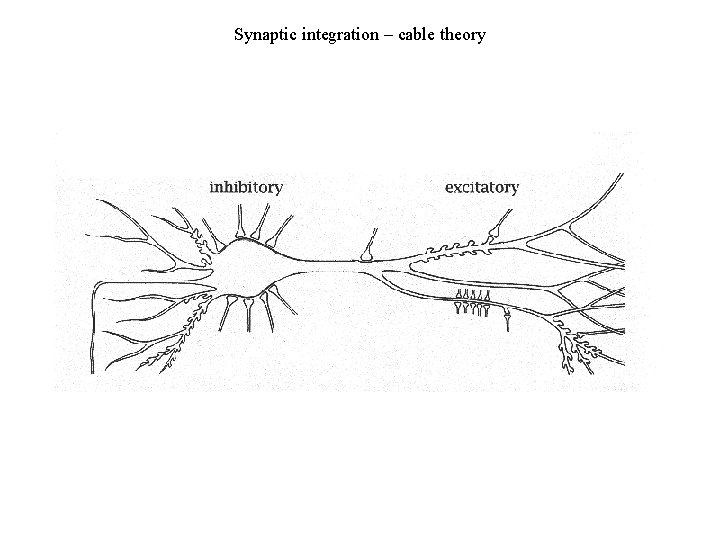
Synaptic integration – cable theory

Isopotential sphere Current injected into a spherical cell will distribute uniformly across the surface of the sphere. The current flowing across a unit area of the membrane: For a finite step of current: For a sphere, a relationship between Im and I 0 is: where The input resistance: - time constant After the current step: The input resistance of a sphere: For long impulse Im (t -> inf) - stan ustalony

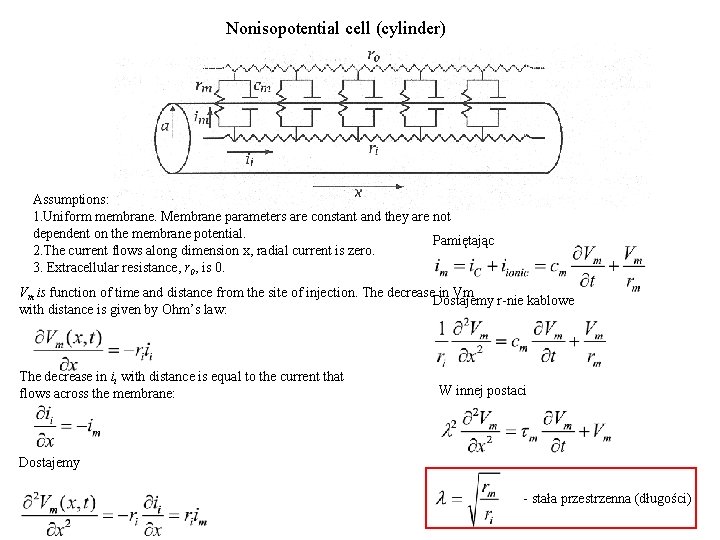
Nonisopotential cell (cylinder) Assumptions: 1. Uniform membrane. Membrane parameters are constant and they are not dependent on the membrane potential. Pamiętając 2. The current flows along dimension x, radial current is zero. 3. Extracellular resistance, r 0, is 0. Vm is function of time and distance from the site of injection. The decrease in Vm Dostajemy r-nie kablowe with distance is given by Ohm’s law: The decrease in ii with distance is equal to the current that flows across the membrane: W innej postaci Dostajemy - stała przestrzenna (długości)

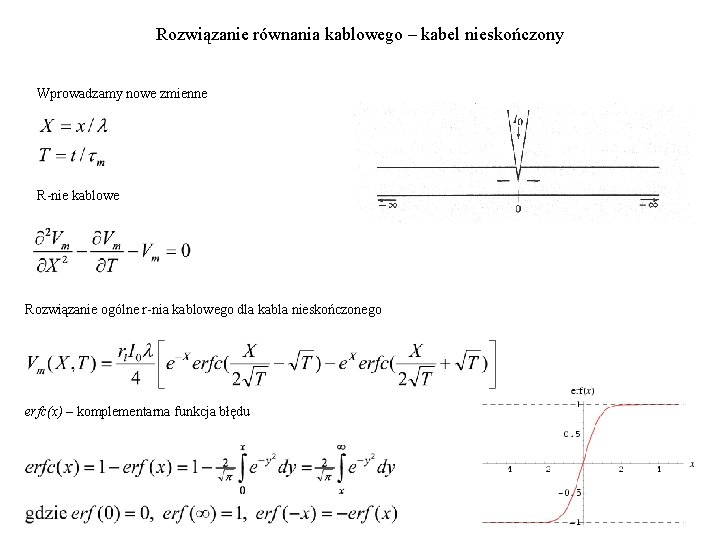
Rozwiązanie równania kablowego – kabel nieskończony Wprowadzamy nowe zmienne R-nie kablowe Rozwiązanie ogólne r-nia kablowego dla kabla nieskończonego erfc(x) – komplementarna funkcja błędu

Rozwiązanie równania kablowego – kabel nieskończony Rozwiązanie stacjonarne Szukamy rozwiązania stacjonarnego lub Znaczenie l: l określa własności kabla w stanie ustalonym; jest to odległość, na której napięcie w stanie ustalonym maleje e razy. Opór wejściowy - kabel nieskończony Opór wejściowy - kabel półnieskończony

Rozwiązanie równania kablowego – kabel nieskończony Rozwiązanie przejściowe Szukamy rozwiązania przejściowego dla X = 0 Kabel nieskończony Kabel półnieskończony

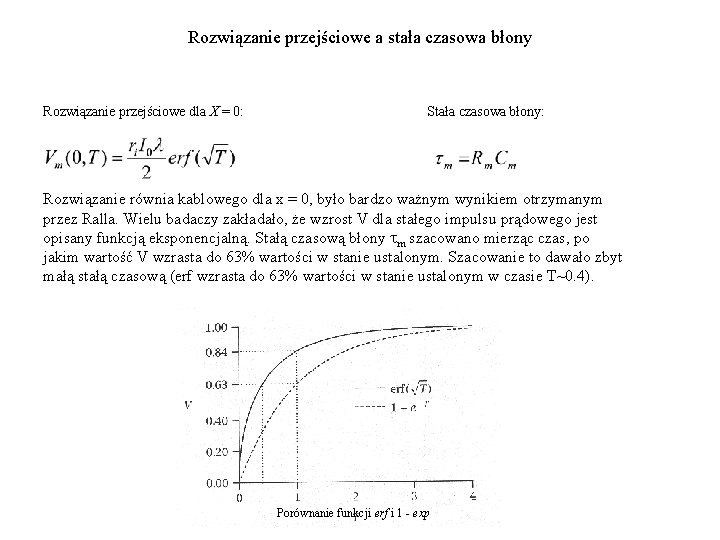
Rozwiązanie przejściowe a stała czasowa błony Rozwiązanie przejściowe dla X = 0: Stała czasowa błony: Rozwiązanie równia kablowego dla x = 0, było bardzo ważnym wynikiem otrzymanym przez Ralla. Wielu badaczy zakładało, że wzrost V dla stałego impulsu prądowego jest opisany funkcją eksponencjalną. Stałą czasową błony tm szacowano mierząc czas, po jakim wartość V wzrasta do 63% wartości w stanie ustalonym. Szacowanie to dawało zbyt małą stałą czasową (erf wzrasta do 63% wartości w stanie ustalonym w czasie T~0. 4). Porównanie funkcji erf i 1 - exp

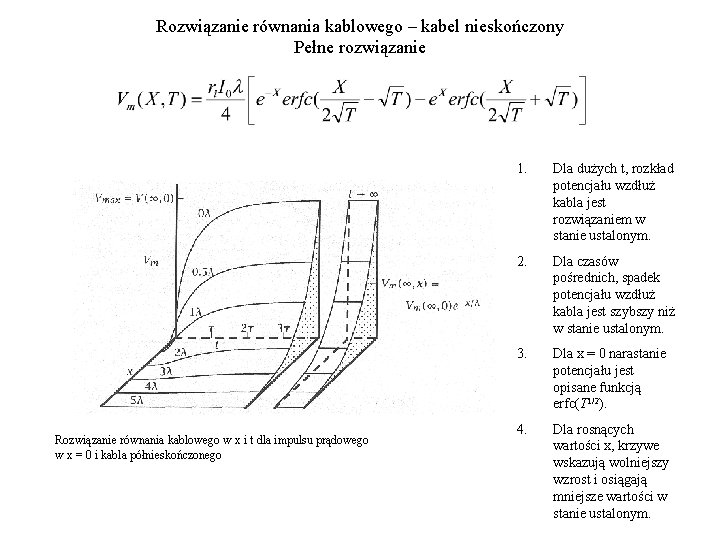
Rozwiązanie równania kablowego – kabel nieskończony Pełne rozwiązanie Rozwiązanie równania kablowego w x i t dla impulsu prądowego w x = 0 i kabla półnieskończonego 1. Dla dużych t, rozkład potencjału wzdłuż kabla jest rozwiązaniem w stanie ustalonym. 2. Dla czasów pośrednich, spadek potencjału wzdłuż kabla jest szybszy niż w stanie ustalonym. 3. Dla x = 0 narastanie potencjału jest opisane funkcją erfc(T 1/2). 4. Dla rosnących wartości x, krzywe wskazują wolniejszy wzrost i osiągają mniejsze wartości w stanie ustalonym.

Rozwiązanie równania kablowego – kabel skończony Rozwiązanie stacjonarne I 0 R-nie kablowe x=0 W stanie ustalonym x=l Warunki brzegowe dla x = l - koniec zamknięty - koniec otwarty Dostajemy Nowe zmienne - odległość elektrotoniczna - długość elektrotoniczna Rozwiązanie ogólne Cosinus i sinus hiperboliczny

Rozwiązanie równania kablowego – kabel skończony Rozwiązanie stacjonarne Rozwiązanie ogólne możemy zapisać Lub Dla X = L Podstawmy BL = C 2/VL i wstawmy do równania: BL jest warunkiem brzegowym dla różnego rodzaju zakończenia kabla. Dla X = 0: Lub

Rozwiązanie równania kablowego – kabel skończony Rozwiązanie stacjonarne Ostatecznie rozwiązanie stacjonarne Wpływ warunków brzegowych: - przewodnictwo na zakończeniu kabla, 1. Dla - przewodnictwo kabla półnieskończonego czyli tak jak dla kabla półnieskończonego 2. Dla czyli (koniec zamknięty) 3. Dla czyli (koniec otwarty) kabel skończ. zamknięty kabel skończ. otwarty kabel półnieskończ. Zanik napięcia dla impulsu prądowego w x = 0 i kabla skończonego.

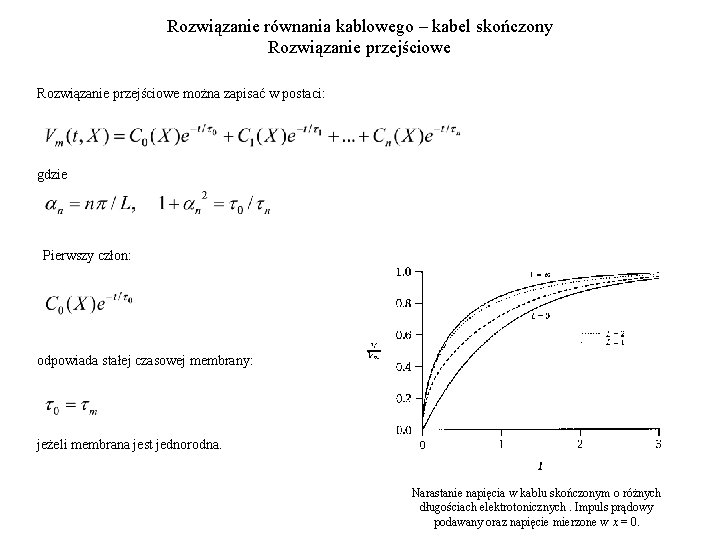
Rozwiązanie równania kablowego – kabel skończony Rozwiązanie przejściowe można zapisać w postaci: gdzie Pierwszy człon: odpowiada stałej czasowej membrany: jeżeli membrana jest jednorodna. Narastanie napięcia w kablu skończonym o różnych długościach elektrotonicznych. Impuls prądowy podawany oraz napięcie mierzone w x = 0.

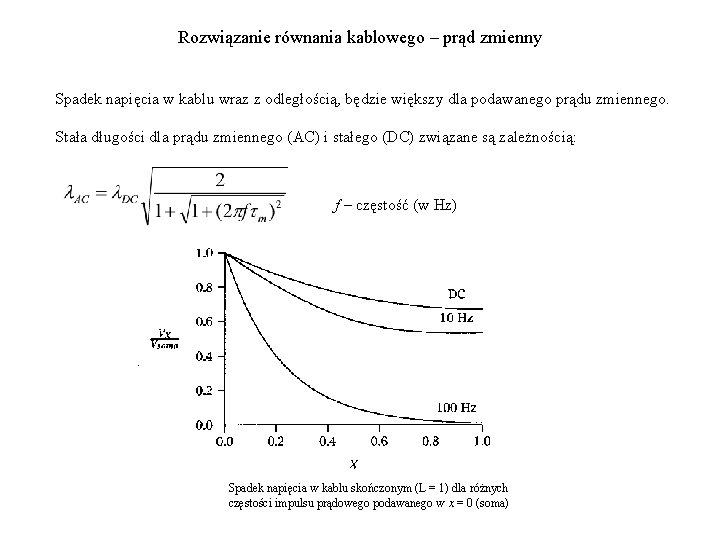
Rozwiązanie równania kablowego – prąd zmienny Spadek napięcia w kablu wraz z odległością, będzie większy dla podawanego prądu zmiennego. Stała długości dla prądu zmiennego (AC) i stałego (DC) związane są zależnością: f – częstość (w Hz) Spadek napięcia w kablu skończonym (L = 1) dla różnych częstości impulsu prądowego podawanego w x = 0 (soma)

Model Ralla W latach 60 -tych i 70 -tych, Wilfred Rall zastosował teorię kablową do analizy sumowania wejść synaptycznych w dendrytach. Założenia 1. Jednorodne właściwości membrany Ri, Rm, Cm 2. R 0 = 0 3. Izopotencjalna soma, najczęściej – izopotencjalna sfera. 4. Wszystkie dendryty mają tą samą długość elektrotoniczną

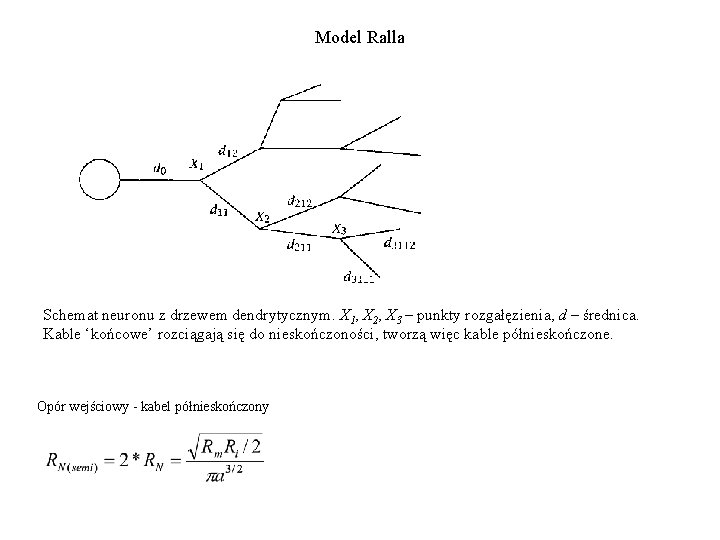
Model Ralla Schemat neuronu z drzewem dendrytycznym. X 1, X 2, X 3 – punkty rozgałęzienia, d – średnica. Kable ‘końcowe’ rozciągają się do nieskończoności, tworzą więc kable półnieskończone. Opór wejściowy - kabel półnieskończony

Model Ralla - cd Opór wejściowy - kabel półnieskończony Przewodnictwo - kabel półnieskończony Upraszczając Przewodnictwo gałęzi d 3111 Oraz podobnie dla d 3112 Przewodnictwo w punkcie X 3 Jeśli w punkcie X 3 przedłużymy d 211 do nieskończoności to Jeśli to gałęzie d 3111 i d 3112 są równoważne matematycznie rozciągnięciu gałęzi d 211 do nieskończoności!

Model Ralla - cd Jeśli zrobimy taką samą operacje dla gałęzi d 212, to w X 2 mamy dwa półnieskończone kable d 211 i d 212 przyłączone do gałęzi d 11. Jeśli Stosując regułę potęgi 3/2 to co jest równoważne rozciągnięciu gałęzi d 11 do nieskończoności. możemy zredukować drzewo dendrytyczne o dowolnej ilości rozgałęzień do równoważnego kabla półnieskończonego. Wiele rzeczywistych drzew dendrytycznych w neuronach kory i hipokampa wykazuje regułę potegi 3/2.

Model Ralla – cd Równoważny kabel skończony Dla dendrytów, zazwyczaj l < 2 l, co odpowiada kablowi skończonemu. Przewodnictwo dla kabla skończonego również zwiera element d 3/2. L – długość elektrotoniczna, taka sama dla wszystkich dendrytów. Korzystając z zależności: Można zapisać: Stosując regułę potęgi 3/2 oraz założenie, że wszystkie dendryty maja takie same L możemy zredukować dowolne drzewo dendrytyczne do równoważnego kabla skończonego. Pamiętając, że dla pojedynczego kabla, L = l/l, można zapisać całkowitą długość elektrotoniczna kabla równoważnego:

Model Ralla – zastosowanie do impulsów synaptycznych Krótki impuls prądowy podawany w somie, w połowie kabla i na końcu kabla Wnioski z modelu: - amplituda EPSP w somie maleje wraz z odległością powstania impulsu - stała narastania oraz pozycja maksimum maleje z odległością powstania impulsu - końcowa stała zaniku jest taka sama dla wszystkich odległości

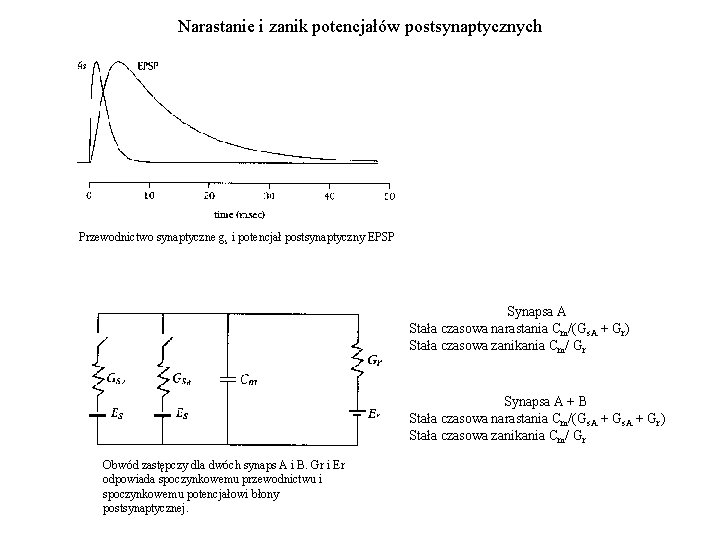
Narastanie i zanik potencjałów postsynaptycznych Przewodnictwo synaptyczne g s i potencjał postsynaptyczny EPSP Synapsa A Stała czasowa narastania Cm/(Gs. A + Gr) Stała czasowa zanikania Cm/ Gr Synapsa A + B Stała czasowa narastania Cm/(Gs. A + Gr) Stała czasowa zanikania Cm/ Gr Obwód zastępczy dla dwóch synaps A i B. Gr i Er odpowiada spoczynkowemu przewodnictwu i spoczynkowemu potencjałowi błony postsynaptycznej.

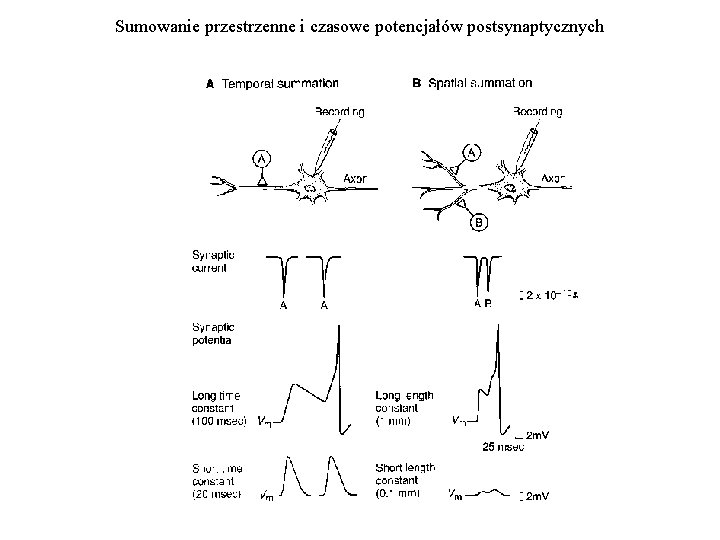
Sumowanie przestrzenne i czasowe potencjałów postsynaptycznych

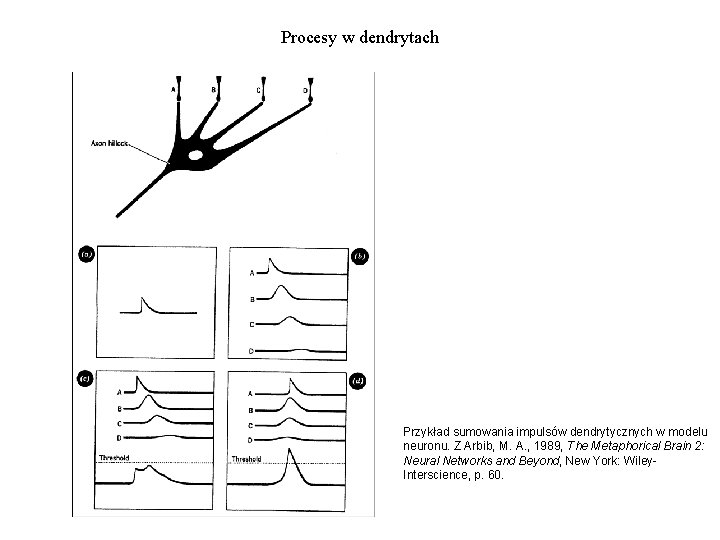
Procesy w dendrytach Przykład sumowania impulsów dendrytycznych w modelu neuronu. Z Arbib, M. A. , 1989, The Metaphorical Brain 2: Neural Networks and Beyond, New York: Wiley. Interscience, p. 60.

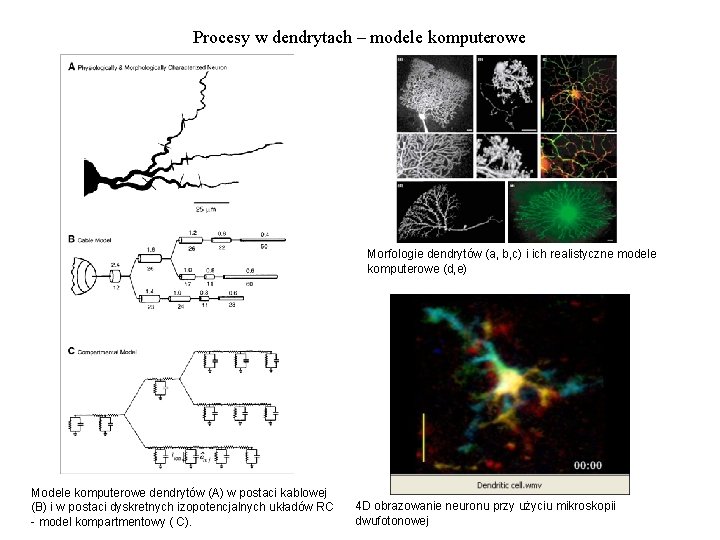
Procesy w dendrytach – modele komputerowe Morfologie dendrytów (a, b, c) i ich realistyczne modele komputerowe (d, e) Modele komputerowe dendrytów (A) w postaci kablowej (B) i w postaci dyskretnych izopotencjalnych układów RC - model kompartmentowy ( C). 4 D obrazowanie neuronu przy użyciu mikroskopii dwufotonowej

Procesy w dendrytach - podsumowanie Z Idan Segev and Michael London Dendritic Processing. Rozdział w M. Arbib (edytor). The Handbook of Brain Theory and Neural Networks. THE MIT PRESS Cambridge, Massachusetts London, England, 2002

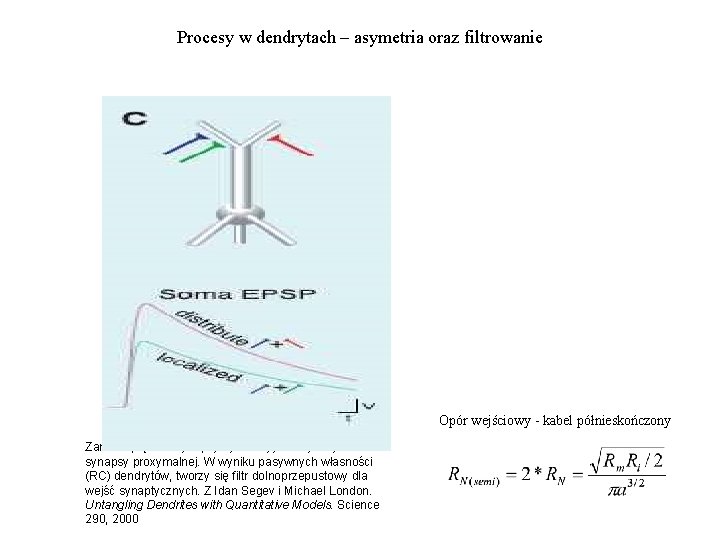
Procesy w dendrytach – asymetria oraz filtrowanie Opór wejściowy - kabel półnieskończony Zanik napięcia z synapsy dystalnej jest szybszy niż z synapsy proxymalnej. W wyniku pasywnych własności (RC) dendrytów, tworzy się filtr dolnoprzepustowy dla wejść synaptycznych. Z Idan Segev i Michael London. Untangling Dendrites with Quantitative Models. Science 290, 2000

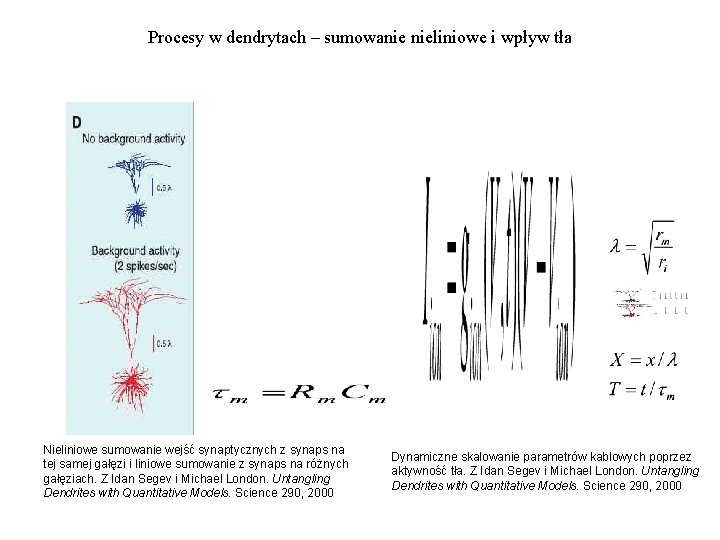
Procesy w dendrytach – sumowanie nieliniowe i wpływ tła Nieliniowe sumowanie wejść synaptycznych z synaps na tej samej gałęzi i liniowe sumowanie z synaps na różnych gałęziach. Z Idan Segev i Michael London. Untangling Dendrites with Quantitative Models. Science 290, 2000 Dynamiczne skalowanie parametrów kablowych poprzez aktywność tła. Z Idan Segev i Michael London. Untangling Dendrites with Quantitative Models. Science 290, 2000

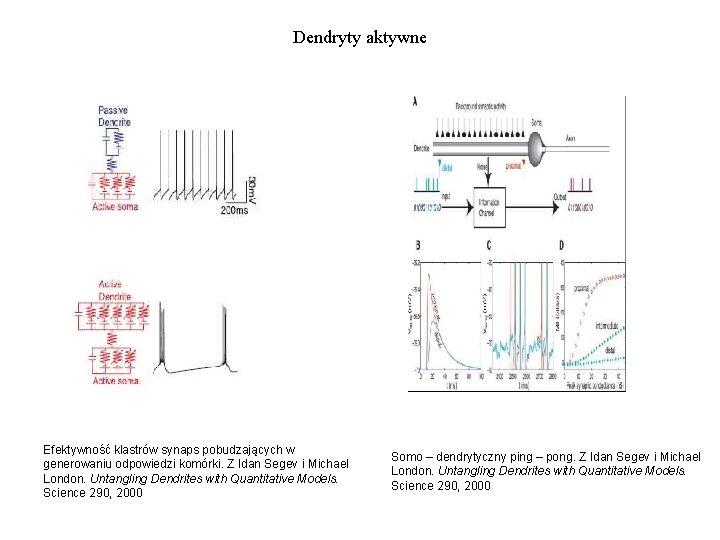
Dendryty aktywne Efektywność klastrów synaps pobudzających w generowaniu odpowiedzi komórki. Z Idan Segev i Michael London. Untangling Dendrites with Quantitative Models. Science 290, 2000 Somo – dendrytyczny ping – pong. Z Idan Segev i Michael London. Untangling Dendrites with Quantitative Models. Science 290, 2000

Kodowanie informacji przez dendryty Analiza wejście –wyjście neuronu przy użyciu analizy informacji. A. 400 synaps pobudzających aktywowanych 10 razy/s i 100 synaps hamujących pobudzanych 65 razy/s w sposób losowy. B. EPSP w somie. C. Pozycja jednej synapsy pobudzającej zmieniona z dystalnej na proxymalną. D. Informacja wzajemna (mutual information MI). Synapsy dystalne przekazują znacząco mniej informacji niż synapsy proxymalne. Z Idan Segev i Michael London. Untangling Dendrites with Quantitative Models. Science 290, 2000