SYMMETRY OF THE STRESS TENSOR The stress tensor

SYMMETRY OF THE STRESS TENSOR The stress tensor ij satisfies the symmetry condition This condition is a consequence of the conservation of momentum. Consider a volume of moving fluid (rather than a fixed volume through which fluid flows in and out) containing mass m, accelerating at rate and subjected to surface force and body (gravitational) force. Newton’s second law requires that Conservation of momentum requires the following. Where an arbitrarily chosen moment arm, denotes 1

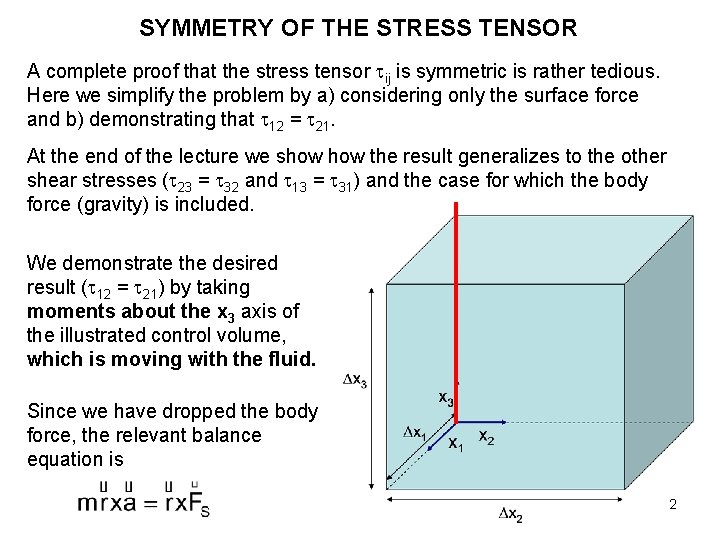
SYMMETRY OF THE STRESS TENSOR A complete proof that the stress tensor ij is symmetric is rather tedious. Here we simplify the problem by a) considering only the surface force and b) demonstrating that 12 = 21. At the end of the lecture we show the result generalizes to the other shear stresses ( 23 = 32 and 13 = 31) and the case for which the body force (gravity) is included. We demonstrate the desired result ( 12 = 21) by taking moments about the x 3 axis of the illustrated control volume, which is moving with the fluid. Since we have dropped the body force, the relevant balance equation is 2

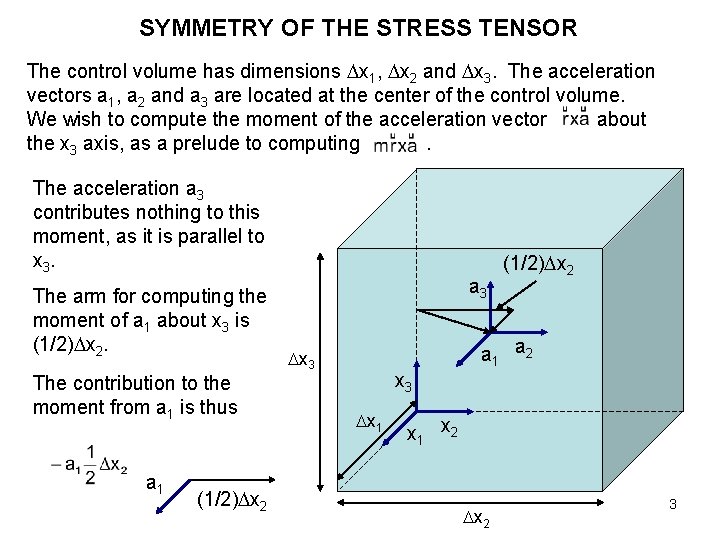
SYMMETRY OF THE STRESS TENSOR The control volume has dimensions x 1, x 2 and x 3. The acceleration vectors a 1, a 2 and a 3 are located at the center of the control volume. We wish to compute the moment of the acceleration vector about the x 3 axis, as a prelude to computing. The acceleration a 3 contributes nothing to this moment, as it is parallel to x 3. The arm for computing the moment of a 1 about x 3 is (1/2) x 2. The contribution to the moment from a 1 is thus a 1 (1/2) x 2 a 3 x 3 x 1 (1/2) x 2 a 1 a 2 x 1 x 2 3

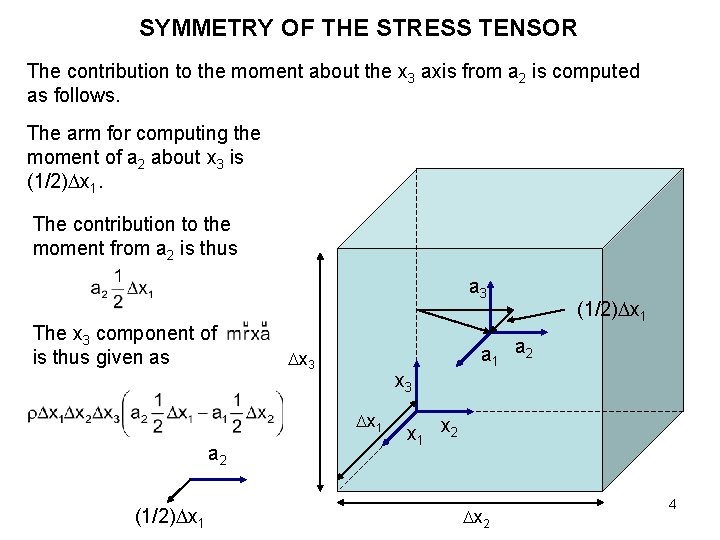
SYMMETRY OF THE STRESS TENSOR The contribution to the moment about the x 3 axis from a 2 is computed as follows. The arm for computing the moment of a 2 about x 3 is (1/2) x 1. The contribution to the moment from a 2 is thus a 3 The x 3 component of is thus given as x 3 x 1 a 2 (1/2) x 1 a 1 a 2 x 1 x 2 4

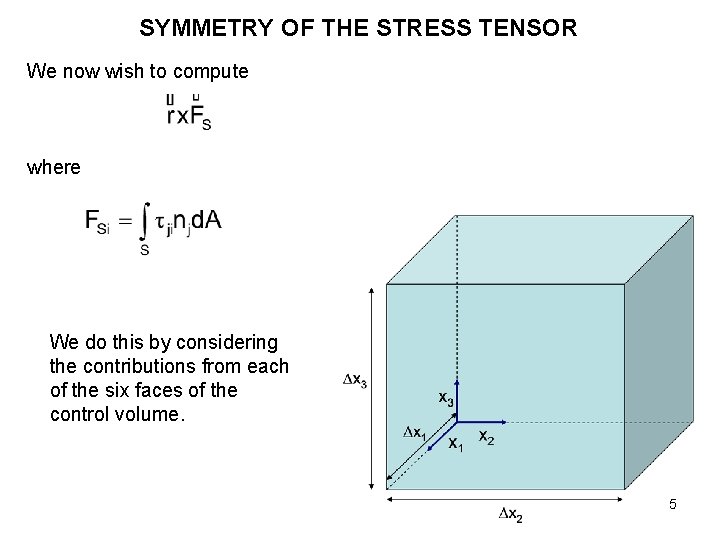
SYMMETRY OF THE STRESS TENSOR We now wish to compute where We do this by considering the contributions from each of the six faces of the control volume. 5

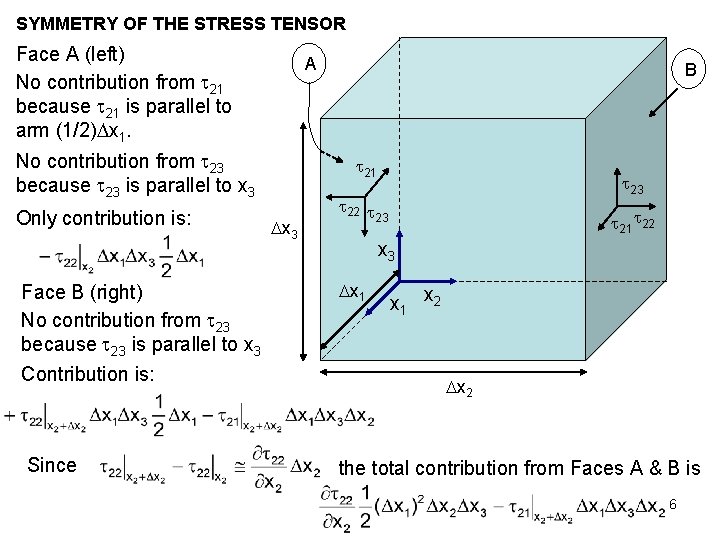
SYMMETRY OF THE STRESS TENSOR Face A (left) No contribution from 21 because 21 is parallel to arm (1/2) x 1. A No contribution from 23 because 23 is parallel to x 3 Only contribution is: Face B (right) No contribution from 23 because 23 is parallel to x 3 Contribution is: Since B 21 x 3 22 23 21 22 x 3 x 1 x 2 the total contribution from Faces A & B is 6

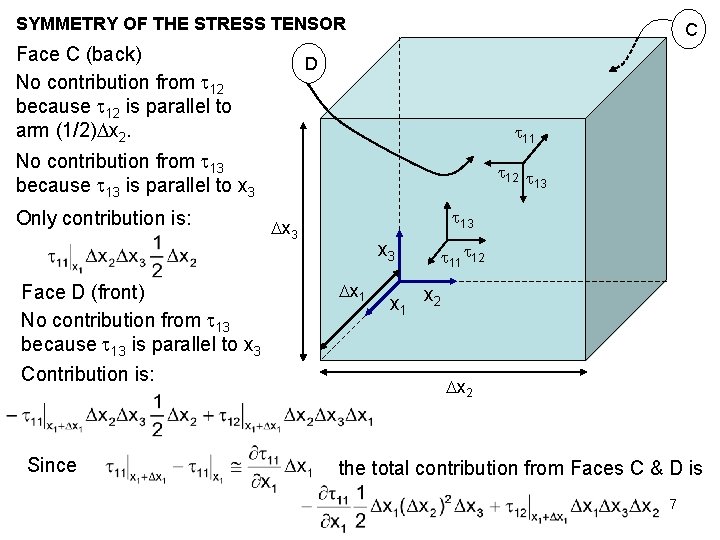
SYMMETRY OF THE STRESS TENSOR Face C (back) No contribution from 12 because 12 is parallel to arm (1/2) x 2. C D 11 No contribution from 13 because 13 is parallel to x 3 Only contribution is: Face D (front) No contribution from 13 because 13 is parallel to x 3 Contribution is: Since 12 13 13 x 3 x 1 11 12 x 1 x 2 the total contribution from Faces C & D is 7

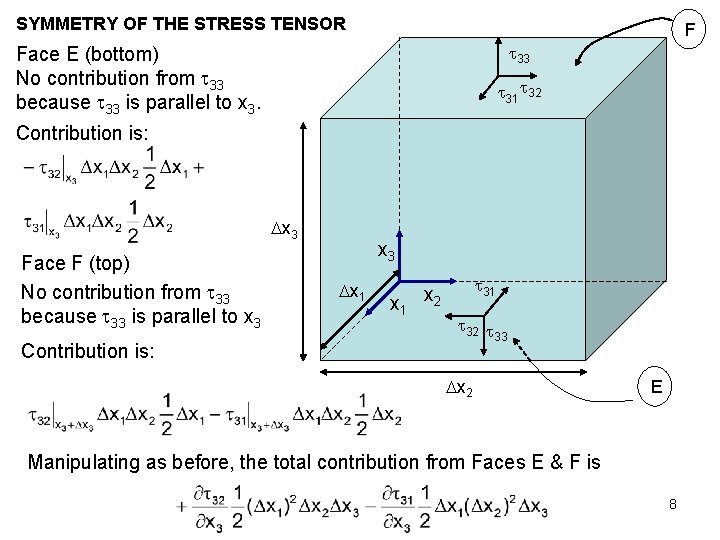
SYMMETRY OF THE STRESS TENSOR F 33 Face E (bottom) No contribution from 33 because 33 is parallel to x 3. 31 32 Contribution is: x 3 Face F (top) No contribution from 33 because 33 is parallel to x 3 Contribution is: x 3 x 1 31 x 2 33 x 2 E Manipulating as before, the total contribution from Faces E & F is 8

SYMMETRY OF THE STRESS TENSOR The sum of moments of the surface force about x 3 axis is equal to so that the x 3 component of the equation reduces to 9

SYMMETRY OF THE STRESS TENSOR Now divide both sides of the equation by x 1 x 2 x 3 to get Taking the limit as x 1, x 2 and x 3 all yields the desired result: 10

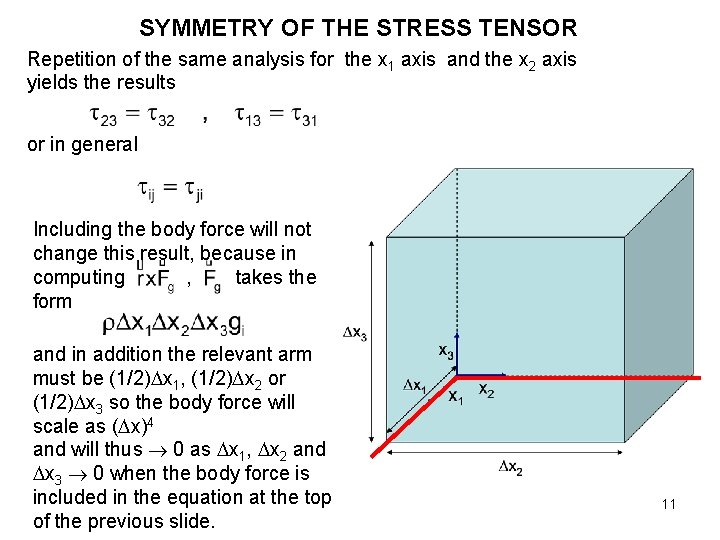
SYMMETRY OF THE STRESS TENSOR Repetition of the same analysis for the x 1 axis and the x 2 axis yields the results or in general Including the body force will not change this result, because in computing , takes the form and in addition the relevant arm must be (1/2) x 1, (1/2) x 2 or (1/2) x 3 so the body force will scale as ( x)4 and will thus 0 as x 1, x 2 and x 3 0 when the body force is included in the equation at the top of the previous slide. 11