SYMMETRY INTRODUCTION Symmetry refers to the property of

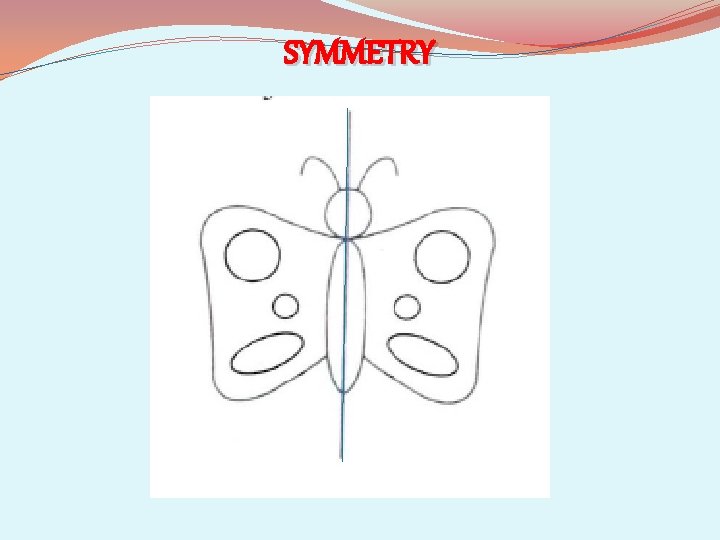
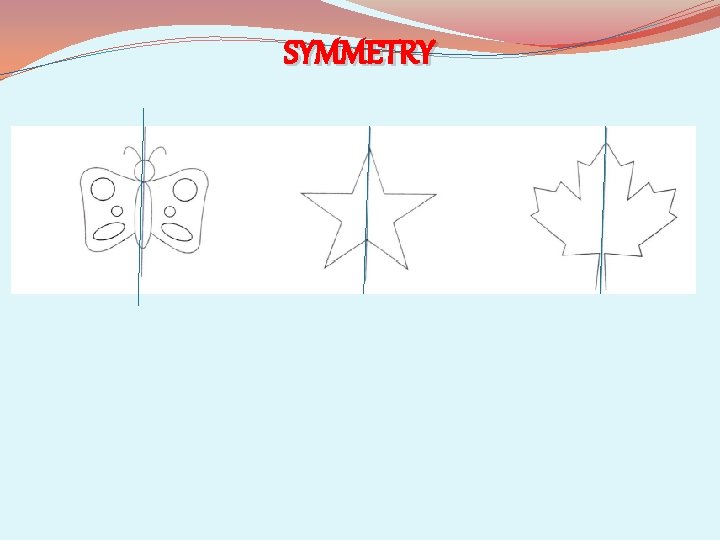
SYMMETRY • INTRODUCTION • Symmetry refers to the property of an object whose one half is identical to the other half. Anything that is symmetrical will be attractive. • The world around us is so beautiful because nature has symmetry in abundance. Birds, animals, trees, flowers, leaves, insects, all display symmetry and the list is endless. We can found symmetry in numbers, alphabets, geometrical shapes, art and even in architecture. The world we live in has a lot of beautiful things. • Most famous and beautiful buildings in the world would appear so because of symmetry. • Few examples to show symmetry in real-life are given below.

SYMMETRY

SYMMETRY

SYMMETRY

SYMMETRY

SYMMETRY

SYMMETRY � SYMMETRY IN ALPHABETS � These are few capital letters of the English alphabet that are symmetrical about their respective lines of symmetry. A, M, T, U, V, Wand Y have one vertical line of symmetry. B, C, D and E have one horizontal line of symmetry. H, I, O and X have two lines of symmetry.

SYMMETRY �SYMMETRY IN GEOMETRY �Symmetry can be seen in various geometrical shapes.

SYMMETRY • Line Segment : - A line segment is symmetrical about its perpendicular bisector. • In the adjoining figure AB is a line segment XY is the perpendicular bisector of AB , so XY is the line of symmetry of AB. • Thus a line segment has one line of symmetry.

SYMMETRY • Angle : - An angle is symmetrical about its angle bisector. • In the adjoining figure BD is the bisector of < ABC , so BD is the line of symmetry of < ABC. • An angle has one line of symmetry.

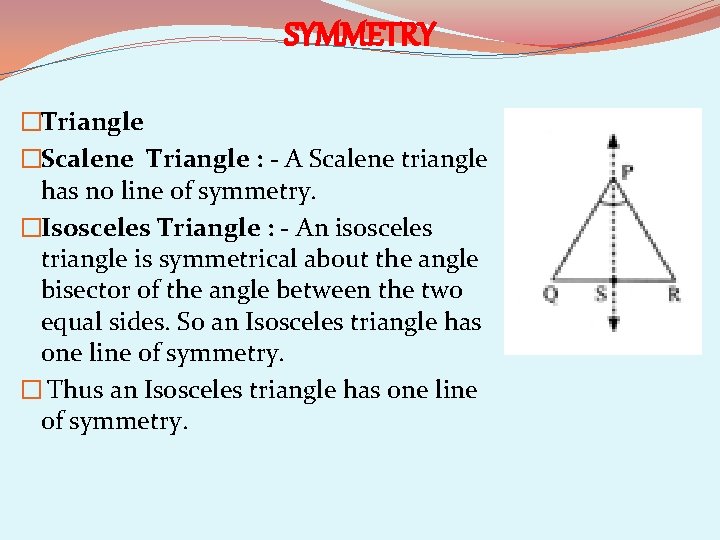
SYMMETRY �Triangle �Scalene Triangle : - A Scalene triangle has no line of symmetry. �Isosceles Triangle : - An isosceles triangle is symmetrical about the angle bisector of the angle between the two equal sides. So an Isosceles triangle has one line of symmetry. � Thus an Isosceles triangle has one line of symmetry.

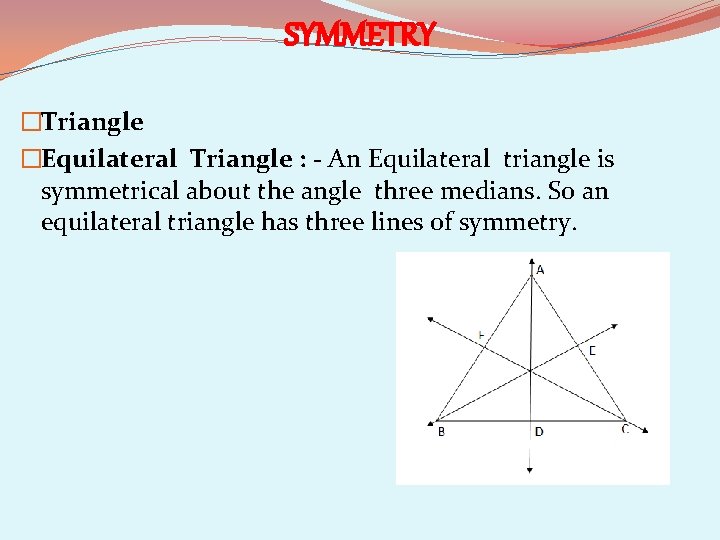
SYMMETRY �Triangle �Equilateral Triangle : - An Equilateral triangle is symmetrical about the angle three medians. So an equilateral triangle has three lines of symmetry.

SYMMETRY �Quadrilateral – �Isosceles Trapezium : - An isosceles trapezium is symmetrical about the line through the midpoint of the parallel sides (bases). �In the adjoining figure, PQRS is an Isosceles Trapezium ( PS = QR ) • Here line AB is the line of symmetry. • Thus an Isosceles trapezium has one line of symmetry.

SYMMETRY �Rectangle : - A rectangle is symmetrical about the lines joining the midpoints of its opposite sides, both vertically and horizontally. So a rectangle has two lines of symmetry. �In the adjoining figure PQRS is a rectangle. • XY and LM are the lines of symmetry of rectangle PQRS. �Thus, a rectangle has two lines of symmetry.

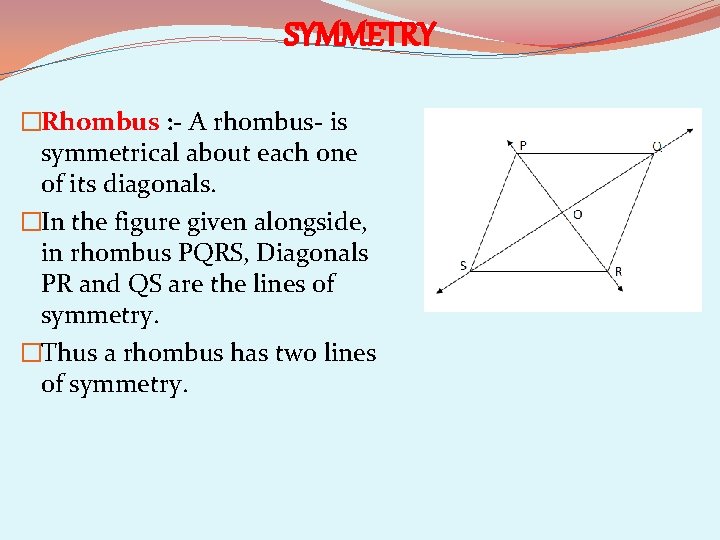
SYMMETRY �Rhombus : - A rhombus- is symmetrical about each one of its diagonals. �In the figure given alongside, in rhombus PQRS, Diagonals PR and QS are the lines of symmetry. �Thus a rhombus has two lines of symmetry.

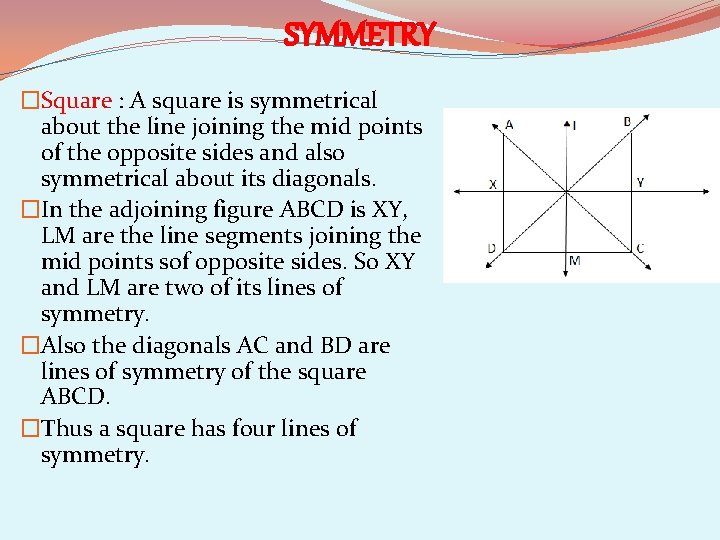
SYMMETRY �Square : A square is symmetrical about the line joining the mid points of the opposite sides and also symmetrical about its diagonals. �In the adjoining figure ABCD is XY, LM are the line segments joining the mid points sof opposite sides. So XY and LM are two of its lines of symmetry. �Also the diagonals AC and BD are lines of symmetry of the square ABCD. �Thus a square has four lines of symmetry.

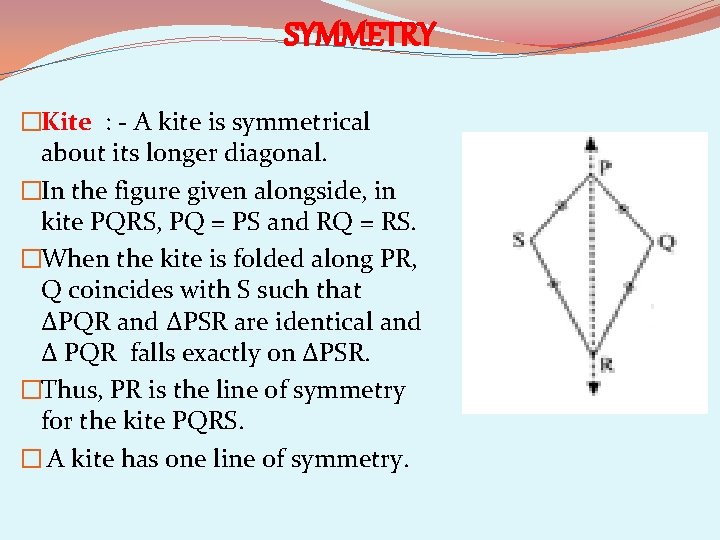
SYMMETRY �Kite : - A kite is symmetrical about its longer diagonal. �In the figure given alongside, in kite PQRS, PQ = PS and RQ = RS. �When the kite is folded along PR, Q coincides with S such that ∆PQR and ∆PSR are identical and ∆ PQR falls exactly on ∆PSR. �Thus, PR is the line of symmetry for the kite PQRS. � A kite has one line of symmetry.

SYMMETRY �Regular Polygons : - A regular polygon is a figure whose all sides are equal. The number of lines of symmetry of a regular polygon is equal to the number of its sides. �An Equilateral triangle has three lines of symmetry �A Square has four lines of symmetry. �A regular pentagon has five lines of symmetry. � A regular hexagon has six lines of symmetry. And so on …

SYMMETRY �Semicircle : - A semicircle is symmetrical above the perpendicular bisector of its diameter. �A semi circle has one line of symmetry.

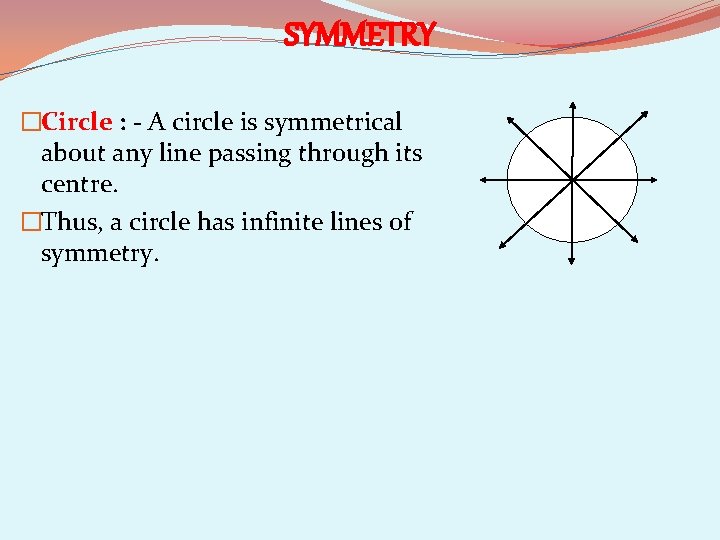
SYMMETRY �Circle : - A circle is symmetrical about any line passing through its centre. �Thus, a circle has infinite lines of symmetry.

SYMMETRY �REFLECTION SYMMETRY �We all know how a mirror reflects an image. The object and its reflection arc symmetrical and the mirror line is the axis of the symmetry. Look at the figures and their mirror images shown below.

SYMMETRY

SYMMETRY �A few examples of reflection symmetry: �Horizontal line of symmetry:

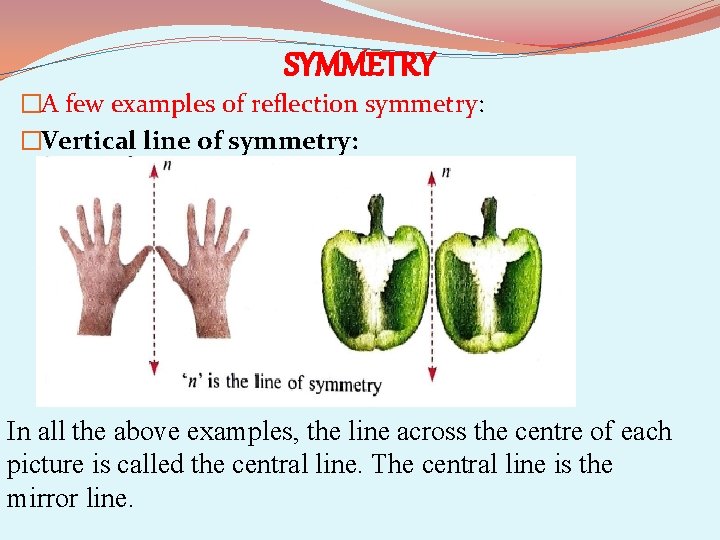
SYMMETRY �A few examples of reflection symmetry: �Vertical line of symmetry: In all the above examples, the line across the centre of each picture is called the central line. The central line is the mirror line.

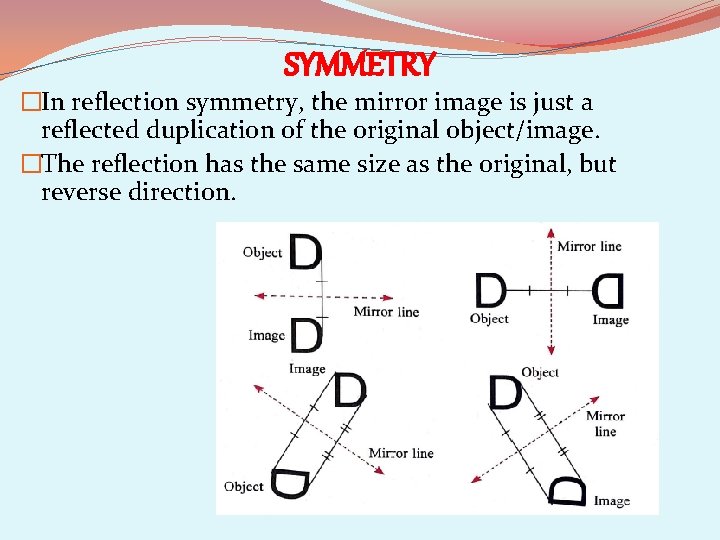
SYMMETRY �In reflection symmetry, the mirror image is just a reflected duplication of the original object/image. �The reflection has the same size as the original, but reverse direction.