Symmetry and the physical properties of crystals Transformation

Symmetry and the physical properties of crystals • Transformation of axes • Vectors and tensors • Neumann’s, Voigt’s and Curie’s principles • Symmetry constraints • Examples

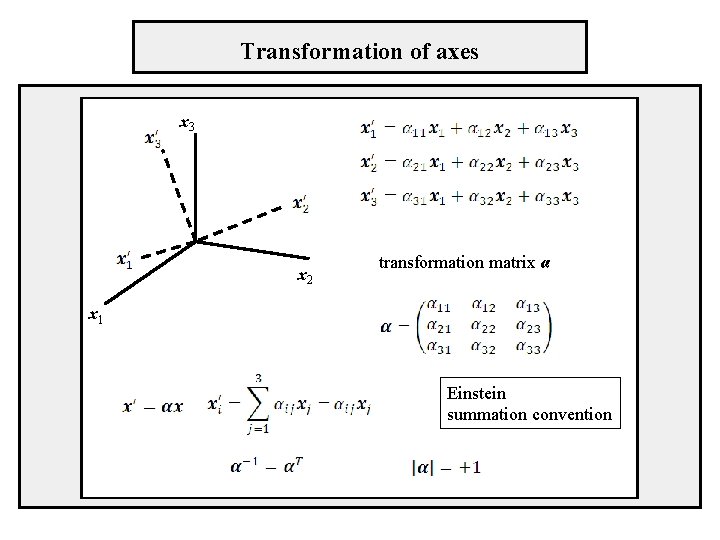
Transformation of axes x 3 x 2 transformation matrix α x 1 Einstein summation convention

Vectors and tensors anisotrophy – general attribute of crystals – dependence on direction properties of materials: link between an independent variable – “stimulus” (vplyvy) and a dependent variable – “response” (odozvy) the variables and the proportionality factors that relate them can be tensors of various rank

Vectors and tensors temperature T – scalar – zero-rank tensor intensity of electric field E, current density i – vectors – tensors of rank one pyroelectric coefficient pi P – polarization vector p – vector – tensor of rank one electrical conductivity s can be described by one ”number”? in general form s = sij – 9 = 32 components (6 independent) – second-rank tensor

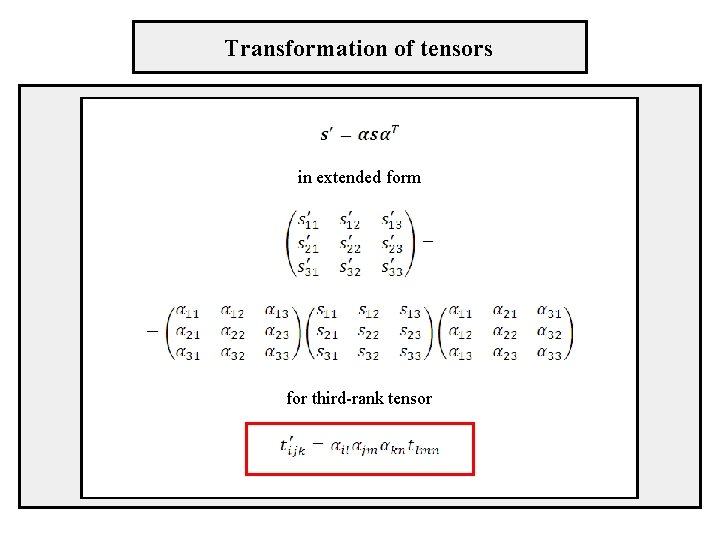
Transformation of tensors vectors axes For transformation of a vector the same matrix has to be used as for the axes for a second-rank tensor in the frame of the new axes x’ therefore

Transformation of tensors in extended form for third-rank tensor

Stress tensor – tenzor napätia Force per unit area [Pa] mechanical equilibrium – normal components – shear components Stress tensor is symmetric

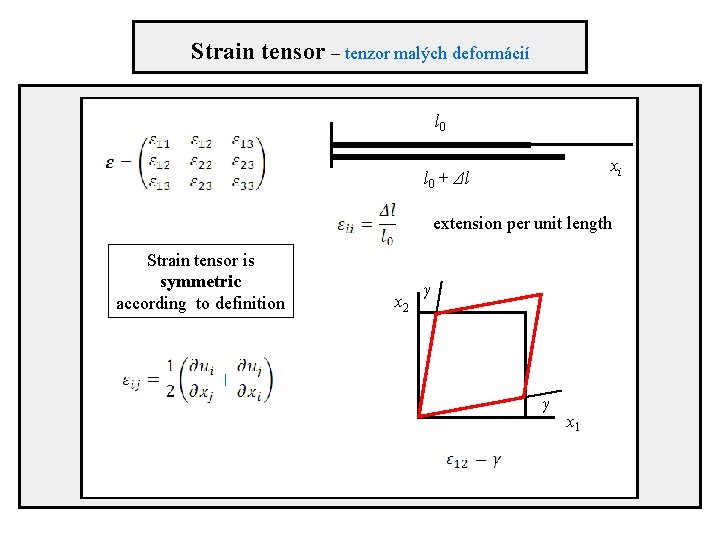
Strain tensor – tenzor malých deformácií l 0 xi l 0 + Δl extension per unit length Strain tensor is symmetric according to definition x 2 γ γ x 1

Voigt notation introduced for symmetric second-rank tensors – simplification for stress indices 11 → 1 22 → 2 33 → 3 23 → 4 13 → 5 12 → 6 for strain

Higher-rank tensors In general, the relationship between a quantity represented by an m-rank tensor and a quantity represented by an n-rank tensor involves a tensor of rank m+n with 3 m+n components. Piezoelectricity Stress applied to certain crystals may develop an electric moment whose magnitude is proportional to the applied stress d σ is the piezoelectric modulus – third-rank tensor is the stress tensor

Hook’s law general form S – compliance tensor – tenzor poddajnosti C – stiffness tensor – tenzor tuhosti written in Voigt notation S and C – 4 th-rank tensors

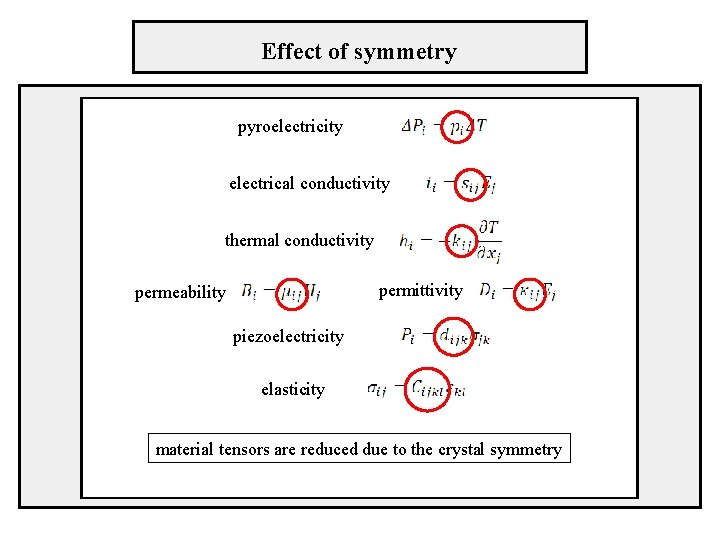
Effect of symmetry pyroelectricity electrical conductivity thermal conductivity permittivity permeability piezoelectricity elasticity material tensors are reduced due to the crystal symmetry

Effect of symmetry Important questions should be answered before starting the experiment • How many values of some physical parameter should be measured? • Which crystal directions give the simplest measurements? • Which directions should give duplicate results? the knowledge of symmetry (point group) and Neumann’s and Voigt’s principles can help to answer these questions

Neumann’s principle The symmetry elements of any physical property of a crystal must include all the symmetry elements of the point group of the crystal, where K denotes the symmetry group of the crystal, GT is the symmetry group of the tensor representing the physical property. The point group K of the crystal must be a subgroup of the symmetry group GT of tensor of the physical property. The magnitude of a particular physical property measured along a specific direction is unchanged when the material is rotated, reflected or inverted into a new orientation corresponding to one of the symmetry elements of its point group.

Voigt’s principle According to Neumann's principle the tensor representing any physical property should be invariant with regard to every symmetry operation of the given crystal class. The condition of invariance reduces the number of the independent tensor components, since it signifies relationships between the tensor components.

Application of Neumann’s principle property described by a second-rank tensor monoclinic crystal with point symmetry group symmetry elements corresponding matrices

Application of Neumann’s principle final form

Application of Neumann’s principle property described by a second-rank tensor tetragonal crystal with point symmetry group x 3 x 2 x 1

Application of Neumann’s principle final form if s is symmetrical

Important remarks Tensors have the simplest form if the coordinate axes are chosen in the directions of the crystal axes with highest symmetry All second-rank symmetrical tensors can be diagonalized by an appropriate choice of coordinate axes Property T in a given direction cosines of n for symmetrical tensors

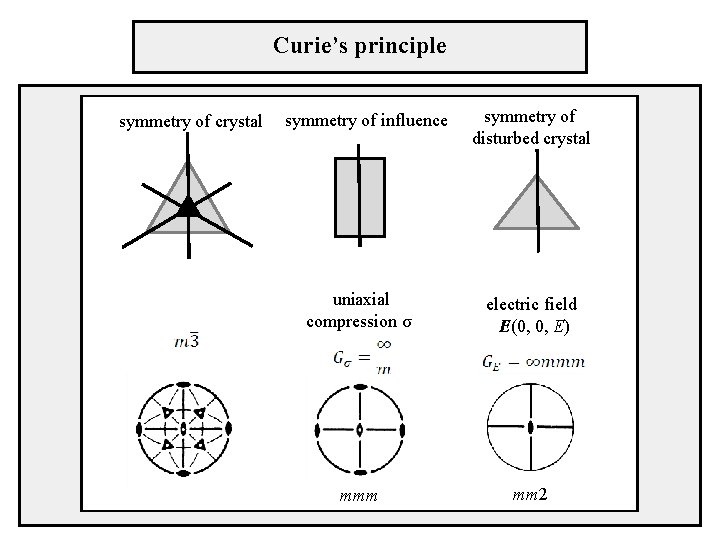
Curie’s principle When certain causes produce certain effects, the symmetry elements of the causes must be found in their effects. The symmetry of the crystal subject to an external influence preserves only the symmetry elements that are common to both the crystal and the perturbing influence. P is the symmetry group of the perturbed crystal, K and G are the symmetry groups of the crystal and of the external influence, respectively.

Curie’s principle symmetry of crystal symmetry of influence symmetry of disturbed crystal uniaxial compression σ electric field E(0, 0, E) mmm mm 2

Examples Pyroelectricity the effect cannot exist in a crystal possessing a centre of symmetry if the crystal possess a unique direction, the polarization vector P lies always along this direction can be present only in crystals with symmetry described by one of ten polar point groups 1, 2, 3, 4, 6, m, mm 2, 3 m, 4 mm and 6 mm Tourmaline, trigonal crystal, symmetry group 3 m Temperature change 1° C produces a polarization 4 x 10 -6 C/m 2 K that is equivalent to the intensity 740 V/cm

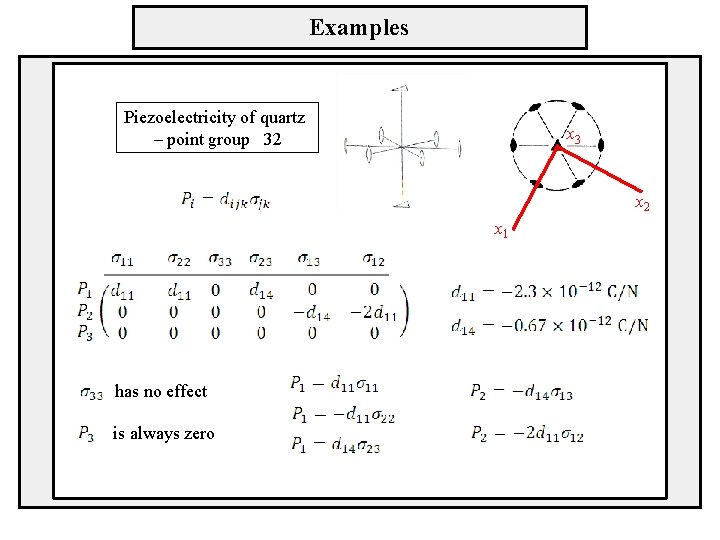
Examples Piezoelectricity of quartz – point group 32 x 3 x 2 x 1 has no effect is always zero

Examples stiffness tensor for hexagonal crystals stiffness tensor for cubic crystals axes parallel to