Symmetry and the Monster One of the greatest




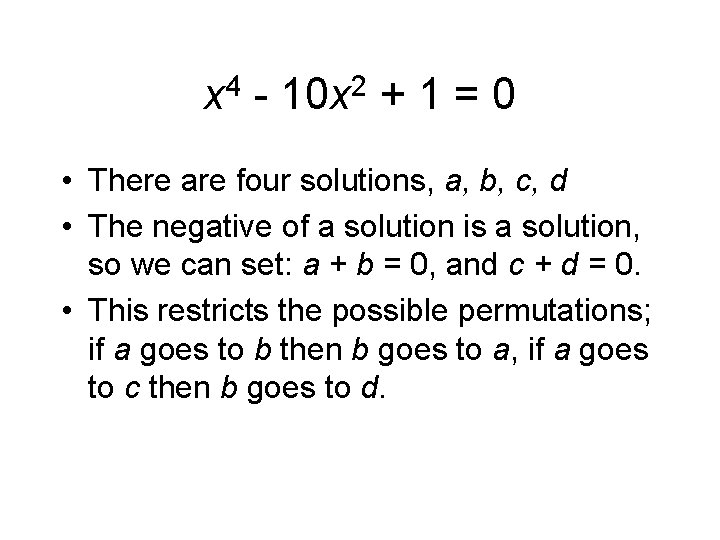



















- Slides: 24

Symmetry and the Monster One of the greatest quests in mathematics

A little early history Equations of degree 2—meaning the highest power of x is x 2: solved by the Babylonians in about 1800 BC Equations of degree 3: solved using a graphical method by Omar Khayyám in about 1100 AD Equations of degrees 3 and 4: solved by Italian mathematicians in the first half of the 1500 s.

The quintic equation • Equations of degree 5 were a problem. No one could come up with a formula. • 1799 Paolo Ruffini • 1824 Niels Hendrik Abel • Early 1830 s Évariste Galois

Galois’s Ideas • If the equation is irreducible any solution is equivalent to any other. • The solutions can be permuted among one another. • Not all permutations are possible, but those that are form the Galois group of the equation.
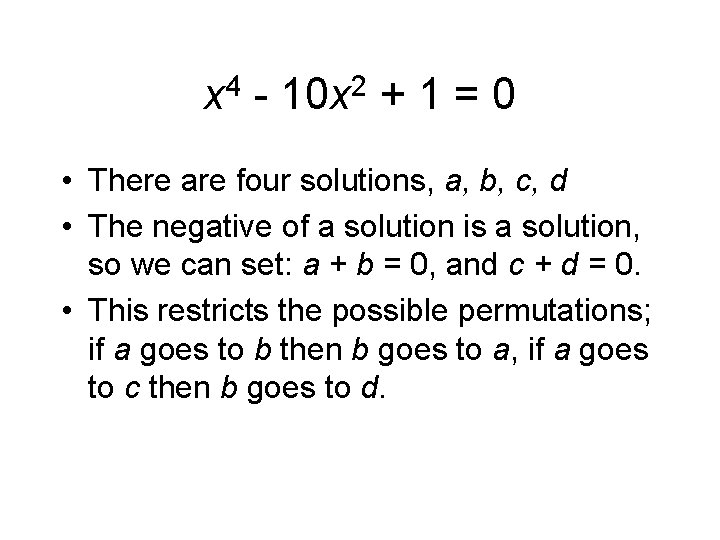
x 4 - 10 x 2 + 1 = 0 • There are four solutions, a, b, c, d • The negative of a solution is a solution, so we can set: a + b = 0, and c + d = 0. • This restricts the possible permutations; if a goes to b then b goes to a, if a goes to c then b goes to d.

The Galois Group • Galois investigated when the solutions to a given equation can be expressed in terms of roots, and when they can’t. • The solutions can be deconstructed into roots precisely when the Galois group can be deconstructed into cyclic groups.

Atoms of Symmetry • A group that cannot be deconstructed into simpler groups is called simple. • For each prime number p the group of rotations of a regular p-gon is simple; it is a cyclic group. • The structure of a non-cyclic simple group can be very complex.

Families of Simple Groups • Galois discovered the first family of noncyclic finite simple groups. • Other families were discovered in the later nineteenth century. • All these families were later seen as ‘groups of Lie type’, stemming from work of Sophus Lie.

Sophus Lie • Lie wanted to do for differential equations what Galois had done for algebraic equations. • He created the concept of continuous groups, now called Lie groups. • ‘Simple’ Lie groups were classified into seven families, A to G, by Wilhelm Killing.

Finite groups of Lie type • Finite versions of Lie groups are called groups of Lie type. • Most of them were created by Leonard Dickson in 1901. • In 1955 Claude Chevalley found a uniform method yielding all families A to G. • Variations on Chevalley’s theme soon emerged, and by 1961 all finite groups of Lie type had been found.

The Feit-Thompson Theorem • In 1963, Walter Feit and John Thompson proved the following big theorem: • A non-cyclic finite simple group must contain an element of order 2. • Elements of order 2 give rise to ‘crosssections’, and Richard Brauer had shown that knowing one cross-section of a finite simple group gave a firm handle on the group itself.

The Classification • By 1965 it looked as if a finite simple group must be a group of Lie type, or one of five exceptions discovered in the mid-nineteenth century. • These five exceptions, the Mathieu groups—created by Émile Mathieu—are very exceptional. There is nothing else quite like them.

A Cat among the Pigeons • In 1966, Zvonimir Janko in Australia produced a sixth exception. • He discovered it via one of its crosssections. • This led Janko and others to search for more exceptions, and within ten years another twenty turned up.

The Exceptions • Some were found using the crosssection method • Some were found by studying groups of permutations • Some were found using geometry

The Hall-Janko group J 2 • Janko found it using the cross-section method. • Marshall Hall found it using permutation groups. • Jacques Tits constructed it using geometry.

The Leech Lattice • John Leech used the largest Mathieu group M 24 to create a remarkable lattice in 24 dimensions. • John Conway studied Leech’s lattice and turned up three new exceptions. • Had he investigated it two years earlier, he would have found two more—the Leech Lattice contains half of the exceptional symmetry atoms.

Fischer’s Monsters • Bernd Fischer in Germany discovered three intriguing and very large permutation groups, modelled on the three largest Mathieu groups. • He then found a fourth one of a different type, and even larger, called the Baby Monster. • Using this as a cross-section, he turned up something even bigger, called the Monster.

Computer Constructions • When the exceptional groups were ‘discovered’, it was not always clear that they existed. • Proving existence could be tricky, and computers were sometimes used. • For example the Baby Monster was constructed on a computer. • BUT the Monster was too large for computer methods.

Constructing the Monster • Fischer, Livingstone and Thorne constructed the character table of the Monster, a 194 -by 194 array of numbers. • This showed the Monster could not live in fewer than 196, 883 dimensions. • 196, 883 = 47 59 71, the three largest primes dividing the size of the Monster. • Later Robert Griess constructed the Monster by hand in 196, 884 dimensions.

Mc. Kay’s Observation • 196, 883 + 1 = 196, 884, the smallest non -trivial coefficient of the j-function. • Mc. Kay wrote to Thompson who had further data on the Monster available. • Thompson confirmed that other dimensions for the Monster seemed to be related to coefficients of the jfunction.

Ogg’s Observation • Shortly after evidence for the Monster was announced, Andrew Ogg attended a lecture in Paris. • Jacques Tits wrote down the size of the Monster, as a product of prime numbers. • Ogg noticed these were precisely the primes that appeared in connection with his own work on the j-function.

Moonshine • The mysterious connections between the Monster and the j-function were dubbed Moonshine. • John Conway and Simon Norton investigated them in detail, proved they were real, and made conjectures about a deeper connection. • Their paper was called Monstrous Moonshine

Vertex Algebras and String Theory • The Moonshine connections involved the Monster acting in finite dimensional spaces. • Frenkel, Leopwski and Meurman combined these in an infinite dimensional space. • Their space had a vertex algebra structure, which brought in the mathematics of string theory.

Conway-Norton Conjectures • The conjectures by Conway and Norton were later proved by Richard Borcherds, who received a Fields Medal for his work, but as he points out, there are still mysteries to resolve • For example the space of ‘j-functions’ associated with the Monster has dimension 163. Is this just a coincidence? • e √ 163 = 262537412640768743. 99999925. . . is very close to being a whole number.
 Symmetry elements ppt
Symmetry elements ppt Willow cabin speech
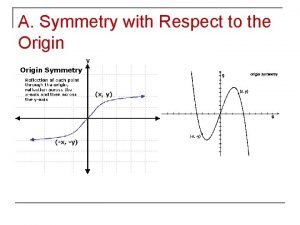
Willow cabin speech With respect to the origin
With respect to the origin Isaac newton one of the greatest
Isaac newton one of the greatest Newton one of the greatest scientists
Newton one of the greatest scientists Isaac newton one of the greatest scientists
Isaac newton one of the greatest scientists One god one empire one religion
One god one empire one religion Little dog run
Little dog run One king one law one faith
One king one law one faith Byzantine definition
Byzantine definition One team one plan one goal
One team one plan one goal See one do one teach one
See one do one teach one See one, do one, teach one
See one, do one, teach one See one do one teach one
See one do one teach one Asean tourism strategic plan
Asean tourism strategic plan Graphic organizer with the aims of la liga filipina
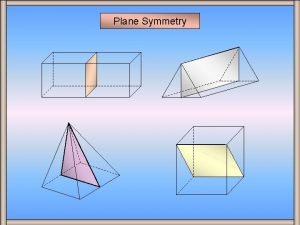
Graphic organizer with the aims of la liga filipina How many planes of symmetry does a hexagonal prism have
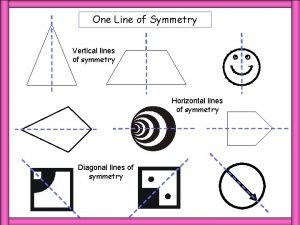
How many planes of symmetry does a hexagonal prism have Shapes of symmetry lines
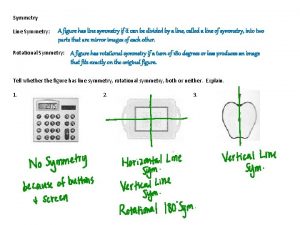
Shapes of symmetry lines How many shapes have more than one line of symmetry
How many shapes have more than one line of symmetry How many lines of symmetry does a kite have
How many lines of symmetry does a kite have The whistling monster
The whistling monster Peter brooks what is a monster
Peter brooks what is a monster General jackson slaying the many headed monster
General jackson slaying the many headed monster I thought i saw a monster poem
I thought i saw a monster poem A trusted officer of odysseus
A trusted officer of odysseus