Symbolic Integral Notation Lesson 5 1 Why Why

Symbolic Integral Notation Lesson 5. 1

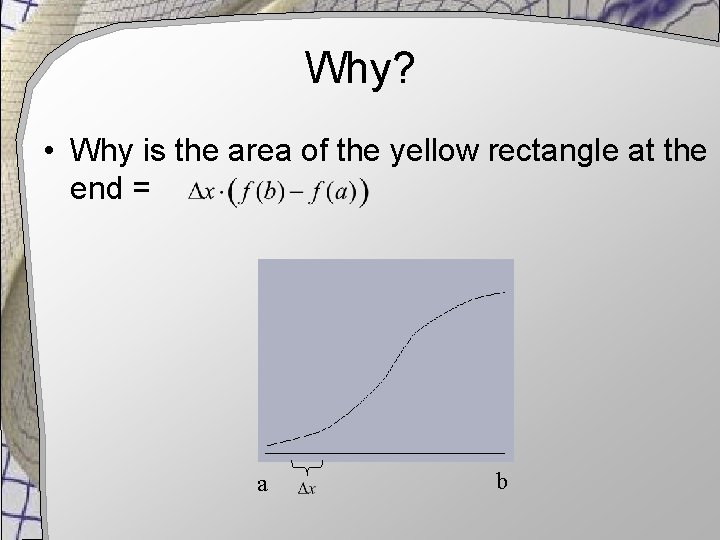
Why? • Why is the area of the yellow rectangle at the end = a b

Review f(x) a b • We partition the interval into n sub-intervals

The Definite Integral • So the definition says that the definite integral of an integrable function can be approximated to within any desired degree of accuracy by a Riemann sum. • We know that if f happens to be positive, then the Riemann sum can be sum f (x *) x interpreted as a sum of If fis(x)the 0, sumtheof. Riemann areas of rectangles. areas of approximating rectangles (see Figure 1). i Figure 1

Review f(x) a x 1 x 2 x 3 b • Evaluate f(x) of kth sub-interval for k = 1, 2, 3, …n • Write an expression for x 1, x 2, and x 3. x 1 = a + 1( ) x 2 = a + 2( ) x 3 = a + 3( )

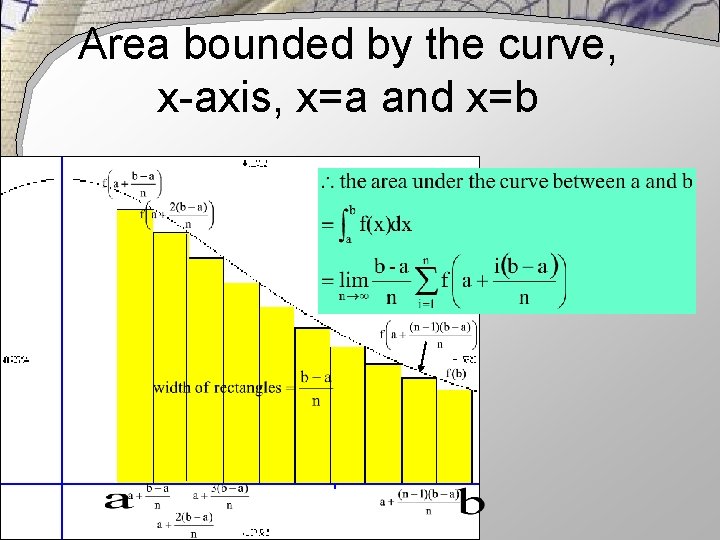
Area bounded by the curve, x-axis, x=a and x=b

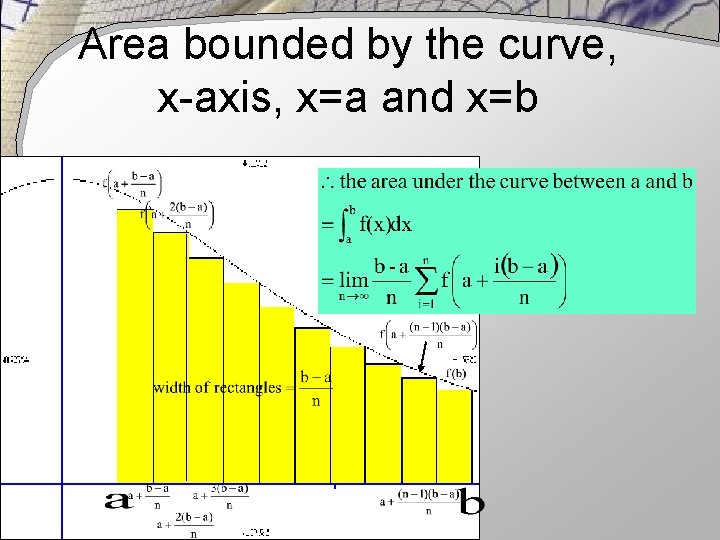
Area bounded by the curve, x-axis, x=a and x=b

Review f(x) a k 1 k 2 k 3 b • What is the area expression for each sub interval?

Review f(x) a k 1 k 2 k 3 b • What is the sum of the area from a to b?

Riemann Sum 3. Form the sum This is the Riemann sum associated with • • • the function f the given partition P the chosen subinterval representatives

The Definite Integral • When Leibniz chose the notation for an integral, he chose • the ingredients as reminders of the limiting process. • In general, when we write • we replace “lim ” by , “. ” by x, and “ x” by dx.

Example 1 • Express • as an integral on the interval [0, ]. • Solution:

The Definite Integral • The definite integral is the limit of the Riemann sum • We say that f is integrable when § the number I can be approximated as accurate as needed by making ||P|| sufficiently small § f must exist on [a, b] and the Riemann sum must exist