Symbolic Finite Automata and M 2 Lstr Margus

Symbolic Finite Automata and M 2 L-str Margus Veanes Aug 30, 2016 IMS, Singapore 1
Key takeaway from this tutorial Best automata I’ve had in a long time, will tell all my friends! Really cool model! Recommended if you like finite alphabets Automata vs • Foundational model for strings/trees over finite alphabets • Great properties (Boolean operations, decidable equivalence) Aug 30, 2016 Symbolic Automata • Foundational model for lists/trees over arbitrary alphabets • Great properties (Boolean operations, decidable equivalence) • Faster, more general, sexier, opportunity for new algorithms IMS, Singapore 2
Some applications • Testing (unit, fuzz) • Regex processing • Web security • SMT extension • Work in progress: Backend for Monadic Second Order logic over finite sequences Aug 30, 2016 IMS, Singapore 3

SFA Application 1 Regexes in parameterized unit testing • Rex component in Pex • Generate values for s that reach the return branches – s is a string of Unicode characters (16 -bit bit-vectors) bool Is. Valid. Email(string s) { string r 1 = @"^[A-Za-z 0 -9]+@(([A-Za-z 0 -9-])+. )+([A-Za-z-])+$"; string r 2 = @"^d. *$"; if (System. Text. Regular. Expressions. Regex. Is. Match(s, r 1)) if (System. Text. Regular. Expressions. Regex. Is. Match(s, r 2)) return false; //branch 1 else Solve: s L(r 1) L(r 2) [eg. s = “ 3@a. b”] return true; //branch 2 else return false; //branch 3 Solve: s L(r 1)L(r 2) [eg. s = “a@b. c”] } Solve: s L(r 1) Aug 30, 2016 IMS, Singapore [eg. s = “a@. . c”] 4

SFA Application 2 Password generation Given constraints: • Length is k: "^[x 21 -x 7 E]{k}$" • Contains 2 capital letters: "[A-Z]. *[A-Z]" • Contains a digit: "d" • Contains a non-word character: "W" Task: Generate random instances with uniform distribution that match all the above conditions. Aug 30, 2016 IMS, Singapore 5

Extensions • output – transducers • lookahead – extended SFAs • trees – symbolic tree automata • registers – symbolic automata/transducers with registers • alternation – alternating SFAs Aug 30, 2016 IMS, Singapore 6

Tutorial Overview Part 1 (s. FAs) Part 2 (Extensions) – symbolic finite automaton or s. FA • properties • key algorithms • Symbolic finite transducer – lookahead • lookahead elimination via Monadic Decomposition – s. M 2 L-str • key difference to M 2 L-str • translation to s. FAs • Cartesian Product of Effective Boolean Algebras Aug 30, 2016 – output IMS, Singapore – tree automata • Minimization – code generation • sequential code gen • parallel code gen 7

Tutorial Overview Part 1 (s. FAs) Part 2 (Extensions) – symbolic finite automaton or s. FA • properties • key algorithms • Symbolic finite transducer – lookahead • lookahead elimination via Monadic Decomposition – s. M 2 L-str • key difference to M 2 L-str • translation to s. FAs • Cartesian Product of Effective Boolean Algebras Aug 30, 2016 – output IMS, Singapore – tree automata • Minimization – code generation • sequential code gen • parallel code gen 8

SYMBOLIC AUTOMATA PROPERTIES Aug 30, 2016 IMS, Singapore 9
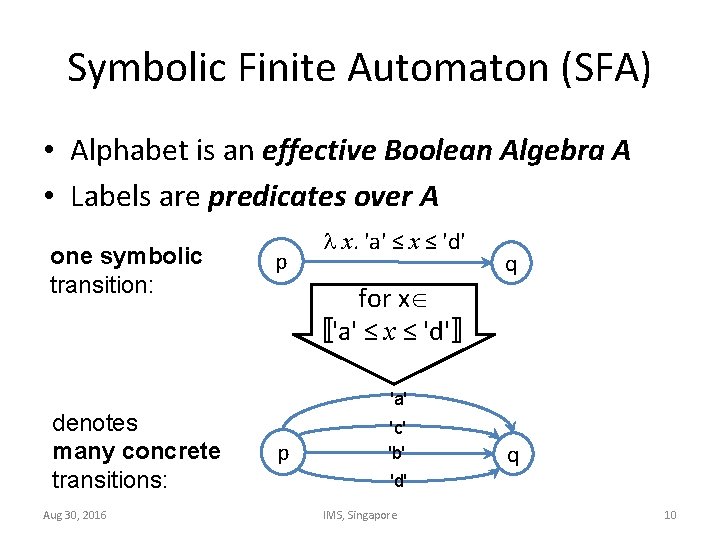
Symbolic Finite Automaton (SFA) • Alphabet is an effective Boolean Algebra A • Labels are predicates over A one symbolic transition: denotes many concrete transitions: Aug 30, 2016 p x. 'a' ≤ x ≤ 'd' q for x 〚'a' ≤ x ≤ 'd'〛 'a' p 'c' 'b' q 'd' IMS, Singapore 10
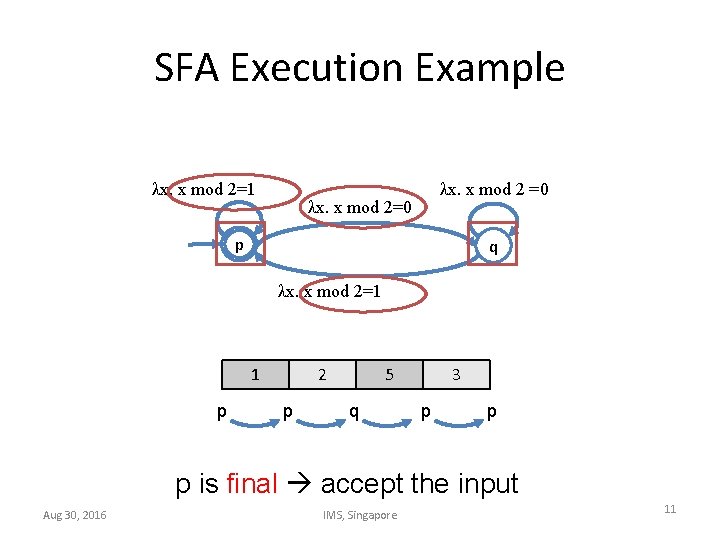
SFA Execution Example λx. x mod 2=1 λx. x mod 2 =0 λx. x mod 2=0 p q λx. x mod 2=1 1 p 2 p 5 q 3 p p p is final accept the input Aug 30, 2016 IMS, Singapore 11
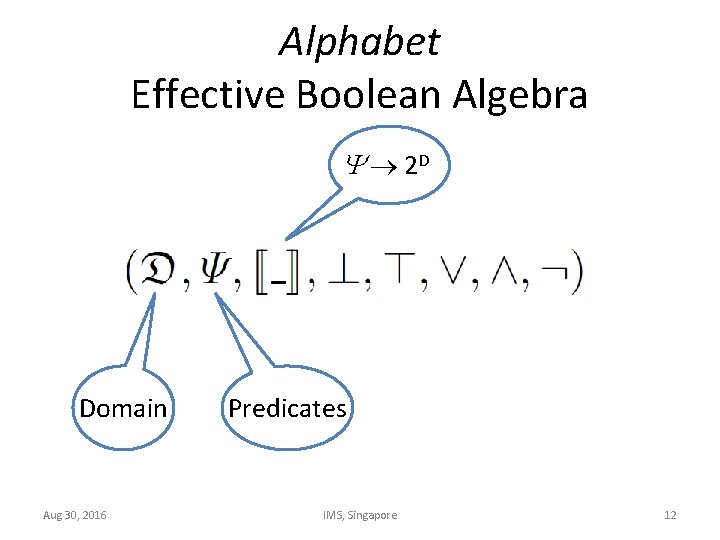
Alphabet Effective Boolean Algebra 2 D Domain Aug 30, 2016 Predicates IMS, Singapore 12

Alphabet SMTint • D = Integers • = integer linear arithmetic formulas (with one fixed free variable) • 〚 〛= 〚 〛 • 〚 〛= , 〚 〛= D 〚 〛 • Satisfiability: 〚 〛 Aug 30, 2016 IMS, Singapore 13
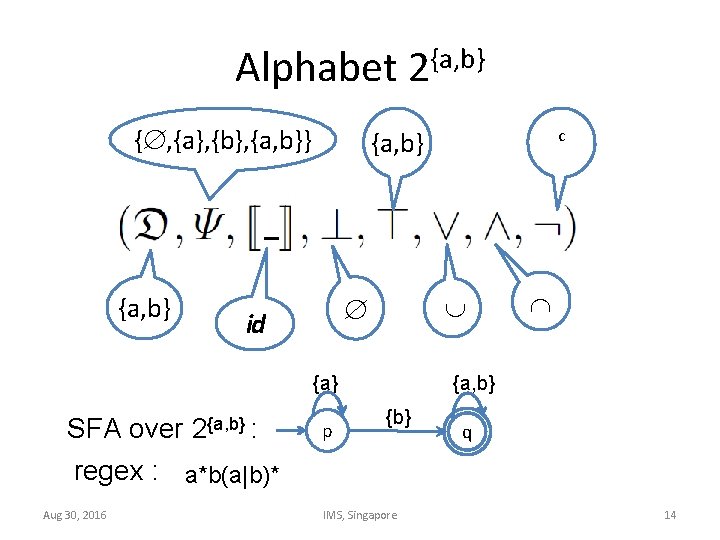
Alphabet 2{a, b} { , {a}, {b}, {a, b}} {a, b} id {a} SFA over 2{a, b} : regex : a*b(a|b)* Aug 30, 2016 c {a, b} p {a, b} {b} IMS, Singapore q 14
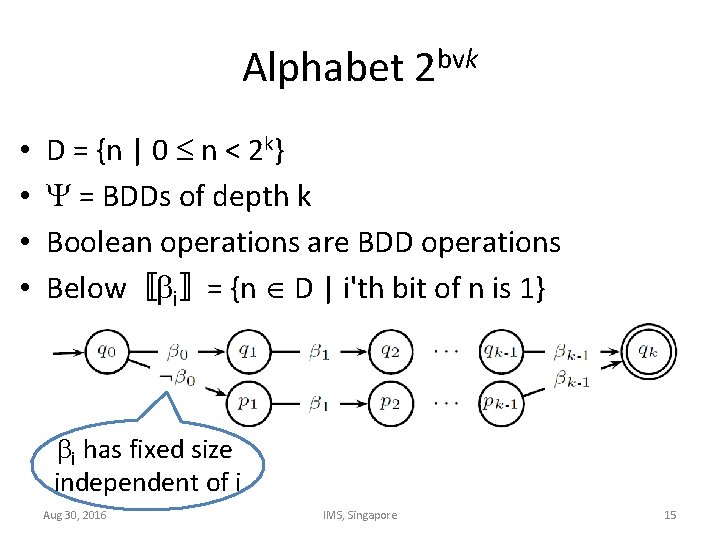
Alphabet 2 bvk • • D = {n | 0 n < 2 k} = BDDs of depth k Boolean operations are BDD operations Below〚 i〛= {n D | i'th bit of n is 1} i has fixed size independent of i Aug 30, 2016 IMS, Singapore 15
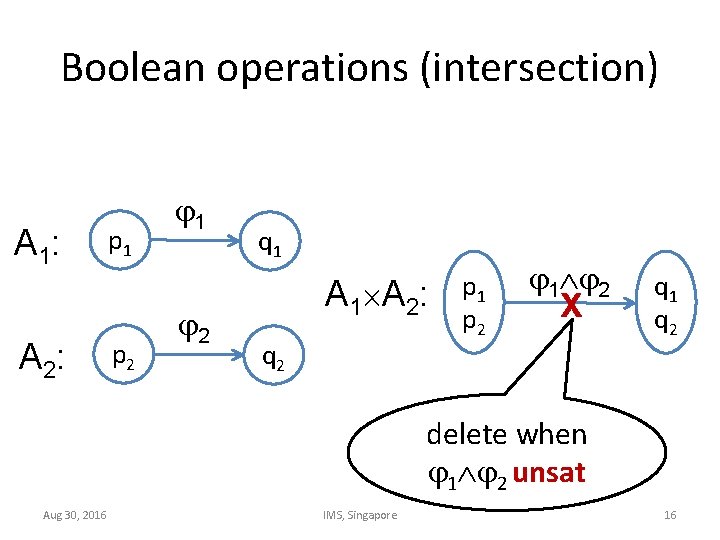
Boolean operations (intersection) A 1: A 2: p 1 p 2 1 2 q 1 A 2: q 2 p 1 p 2 1 2 X q 1 q 2 delete when 1 2 unsat Aug 30, 2016 IMS, Singapore 16
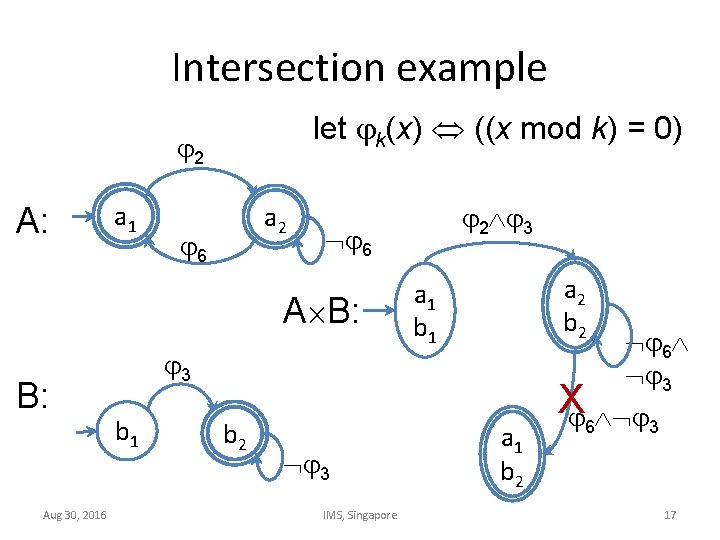
Intersection example let k(x) ((x mod k) = 0) 2 A: a 1 a 2 6 6 A B: B: Aug 30, 2016 3 b 1 b 2 2 3 3 IMS, Singapore a 2 b 2 a 1 b 1 a 1 b 2 6 3 X 6 3 17
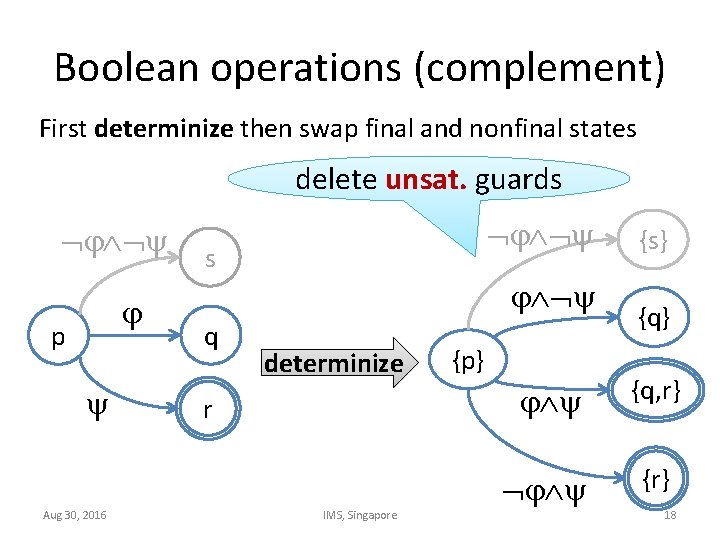
Boolean operations (complement) First determinize then swap final and nonfinal states delete unsat. guards p Aug 30, 2016 s q determinize r IMS, Singapore {p} {s} {q} {q, r} {r} 18

Are SFAs a useful extension of classical automata? • Can classical automata theory and algorithms be extended to work modulo large (infinite) alphabets ? • The answer is nontrivial. For example. – NFA determinization is O(| |2 n) – DFA minimization is O(| |n log n) What happens when is infinite? Aug 30, 2016 IMS, Singapore 19

Why care about symbolic representation at all? One reason: scalability in string analysis – ASCII where | | = 27 – (Unicode strings) UTF 16: | | = 216 – working with character code-points: integers – characters are not opaque • arithmetic operations • intervals Aug 30, 2016 IMS, Singapore 20
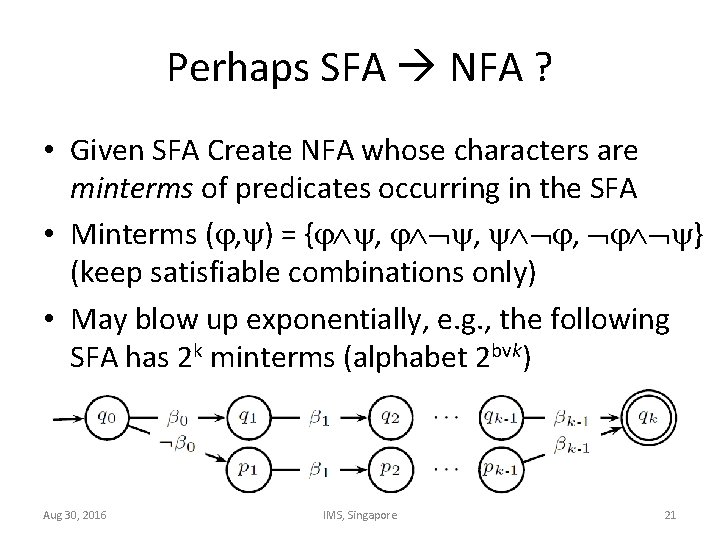
Perhaps SFA NFA ? • Given SFA Create NFA whose characters are minterms of predicates occurring in the SFA • Minterms ( , ) = { , , , } (keep satisfiable combinations only) • May blow up exponentially, e. g. , the following SFA has 2 k minterms (alphabet 2 bvk) Aug 30, 2016 IMS, Singapore 21

SYMBOLIC AUTOMATA KEY ALGORITHMS Aug 30, 2016 IMS, Singapore 22

Minimization 1. What is minimization 2. Classic algorithms 3. A new symbolic algorithm (D’Antoni-Veanes [POPL 14]) Aug 30, 2016 IMS, Singapore 23
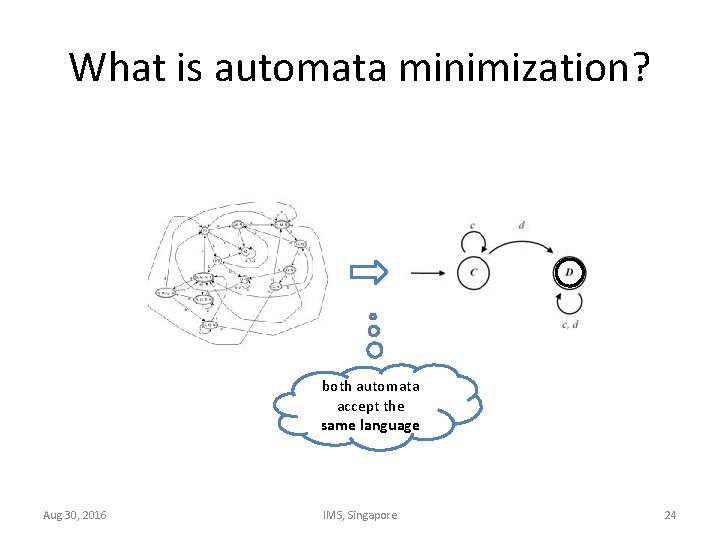
What is automata minimization? both automata accept the same language Aug 30, 2016 IMS, Singapore 24

DFA minimization Minimization = find and collapse all equivalent states (equivalent = not distinguishable) p, q distinguishable: p w s. t. Non final w q Aug 30, 2016 w IMS, Singapore Final 25
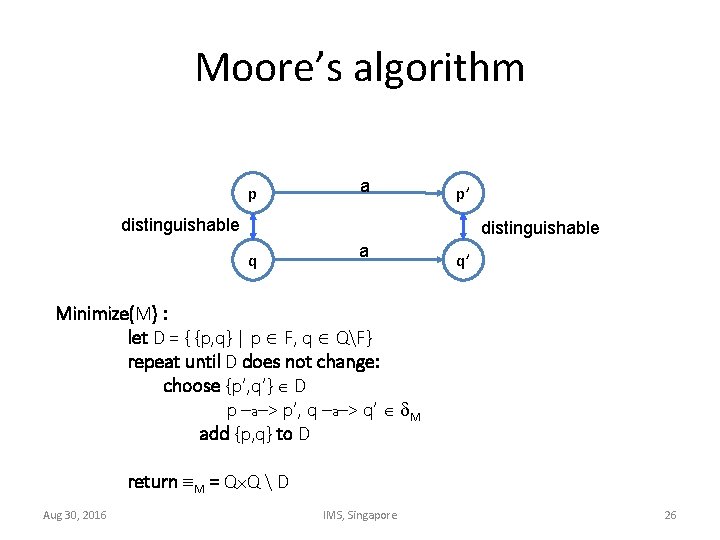
Moore’s algorithm p a p’ distinguishable q a q’ Minimize(M) : let D = { {p, q} | p F, q QF} repeat until D does not change: choose {p’, q’} D p –a–> p’, q –a–> q’ M add {p, q} to D return M = Q Q D Aug 30, 2016 IMS, Singapore 26
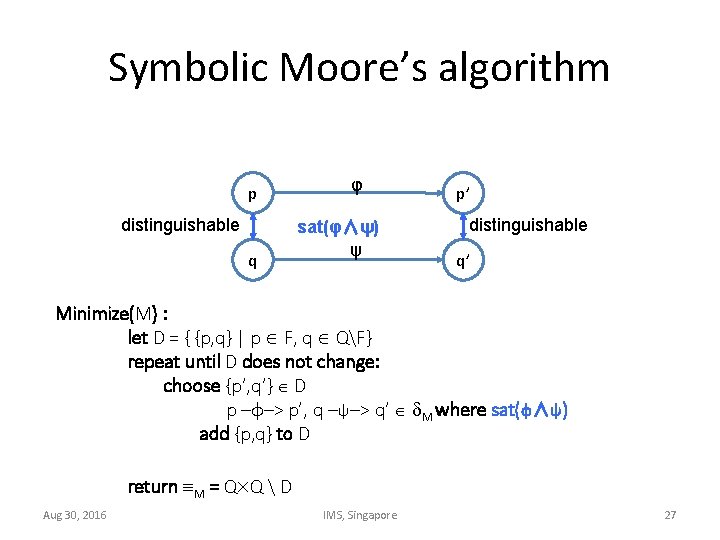
Symbolic Moore’s algorithm p distinguishable q φ sat(φ∧ψ) ψ p’ distinguishable q’ Minimize(M) : let D = { {p, q} | p F, q QF} repeat until D does not change: choose {p’, q’} D p –φ–> p’, q –ψ–> q’ M where sat(φ∧ψ) add {p, q} to D return M = Q Q D Aug 30, 2016 IMS, Singapore 27

Sometimes Moore is Less 18 sec for 15 characters! the culprit should scale up to 128 characters! Aug 30, 2016 IMS, Singapore 28

Hopcroft’s algorithm: intuition QF Aug 30, 2016 F IMS, Singapore 29
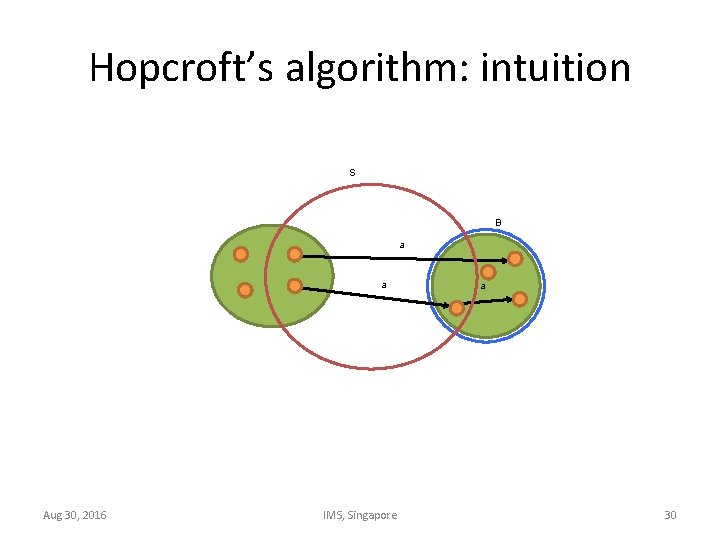
Hopcroft’s algorithm: intuition S B a a Aug 30, 2016 IMS, Singapore a 30
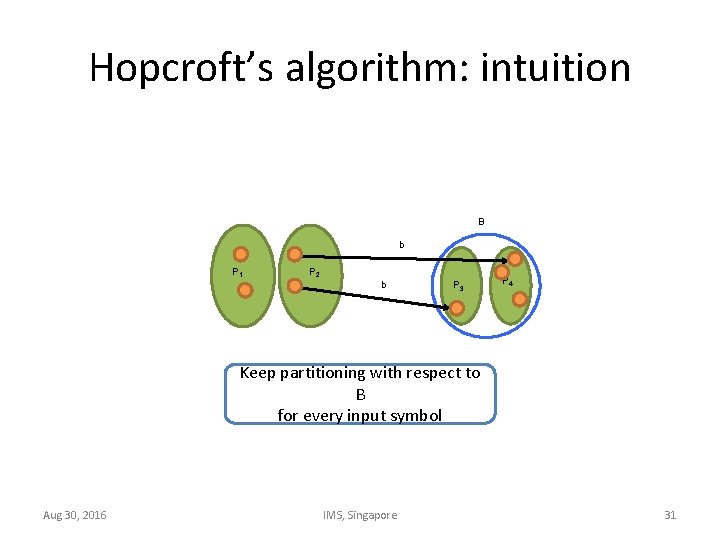
Hopcroft’s algorithm: intuition B b P 1 P 2 b P 3 P 4 Keep partitioning with respect to B for every input symbol Aug 30, 2016 IMS, Singapore 31
Hopcroft’s algorithm: intuition Let’s assume we already split according to B B P 1 P 2 Aug 30, 2016 IMS, Singapore 32
Hopcroft’s algorithm: intuition Let’s assume I already split according to B B P 1 P 2 Do I need to consider both P 1 and for P 2 future splitting? Aug 30, 2016 IMS, Singapore 33
Hopcroft’s algorithm: intuition Let’s assume I already split according to B a B P 1 a a P 2 Do I need to consider both P 1 and for P 2 future splitting? Aug 30, 2016 IMS, Singapore 34
Hopcroft’s algorithm: intuition Let’s assume I already split according to B a B P 1 a a P 2 Do I need to consider both P 1 and for P 2 future splitting? Aug 30, 2016 IMS, Singapore 35
Hopcroft’s algorithm: intuition Let’s assume I already split according to B a P 1 a P 2 Do I need to consider both P 1 and for P 2 future splitting? NO I ONLY NEED ONE! Aug 30, 2016 IMS, Singapore 36

Hopcroft’s algorithm P : = {F, QF} W : = {if |F|< |QF| then F else QF} while W != { } log n iterations R: =pick. From(W) O(| |n log n) foreach a in Σ S : = δ-1(R, a) while ∃ T ∈ P. T∩S ≠ {} ∧ T S ≠ {} P, W : = split(P, P∩S , PS) return collapse states according to P Aug 30, 2016 IMS, Singapore 37

Finitize the alphabet using minterms φ1 φ‘ 1 φ'3 φ3 φ2 φ‘ 5 φ‘ 4 φ‘ 8 φ‘ 6 φ‘ 7 Predicates: {x>5, x<10, x=3} Minterms: {x=3, x≤ 5, 5<x<10, x≥ 10} Aug 30, 2016 IMS, Singapore 38

Symbolic Hopcroft’s algorithm P : = {F, QF} W : = {if |F|< |QF| then F else QF} while W ≠ {} Exponentially many R: =pick. From(W) minterms foreach φ in Minterms(M) S : = δ-1(R, φ) while ∃ B ∈ P: B∩S ≠ ∧ BS ≠ P, W : = split(P, P∩S , PS) return collapse states according to P Aug 30, 2016 IMS, Singapore 39
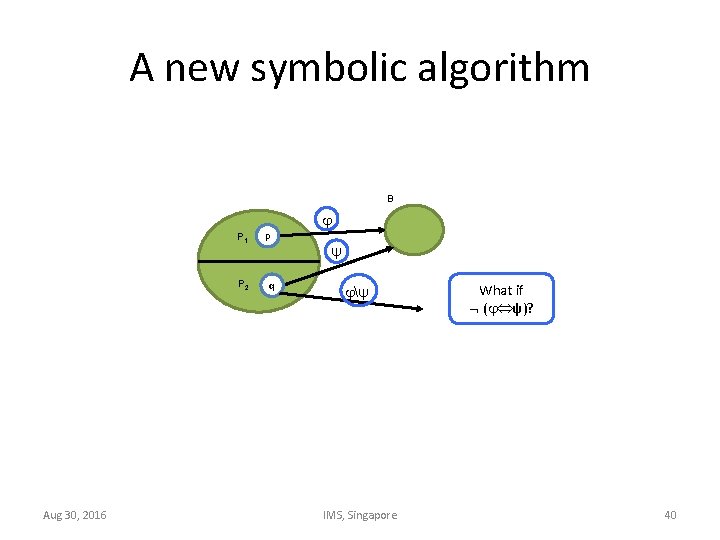
A new symbolic algorithm B P 1 P 2 Aug 30, 2016 p ψ q ψ IMS, Singapore What if ( ψ)? 40
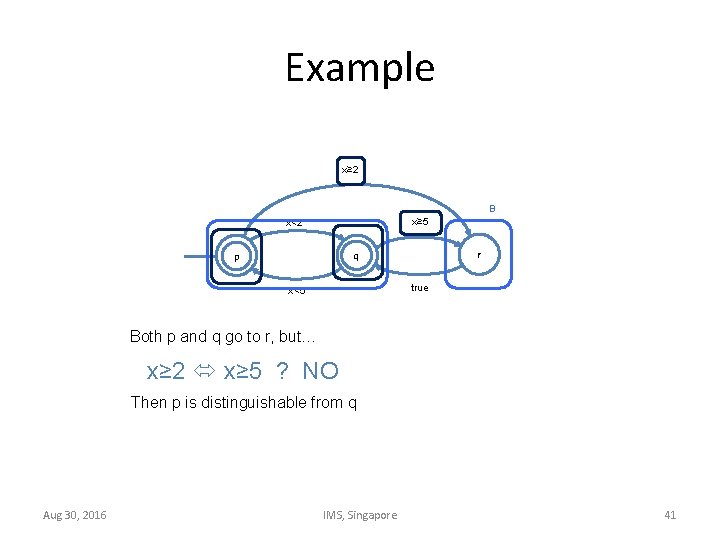
Example x≥ 2 B x≥ 5 x<2 5 p r q 6 true x<5 Both p and q go to r, but… x≥ 2 x≥ 5 ? NO Then p is distinguishable from q Aug 30, 2016 IMS, Singapore 41
Example x≥ 2 B x≥ 5 x<2 5 p true x<5 Aug 30, 2016 r q 6 IMS, Singapore 42

Does it work? Evaluated on 1. Randomly generated DFAs 2. Symbolic automata resulting from real regular expressions 3. Automata with many minterms 4. Symbolic automata over complex theories 5. Automata resulting from Monadic Second Order logic solving Aug 30, 2016 IMS, Singapore 43
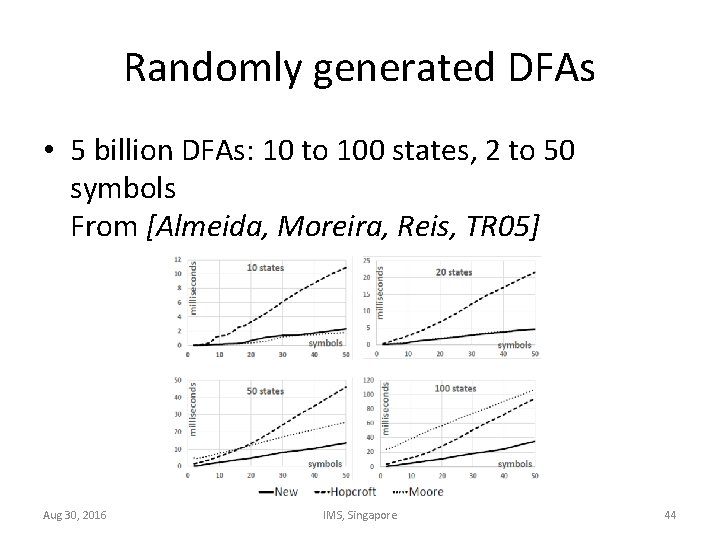
Randomly generated DFAs • 5 billion DFAs: 10 to 100 states, 2 to 50 symbols From [Almeida, Moreira, Reis, TR 05] Aug 30, 2016 IMS, Singapore 44
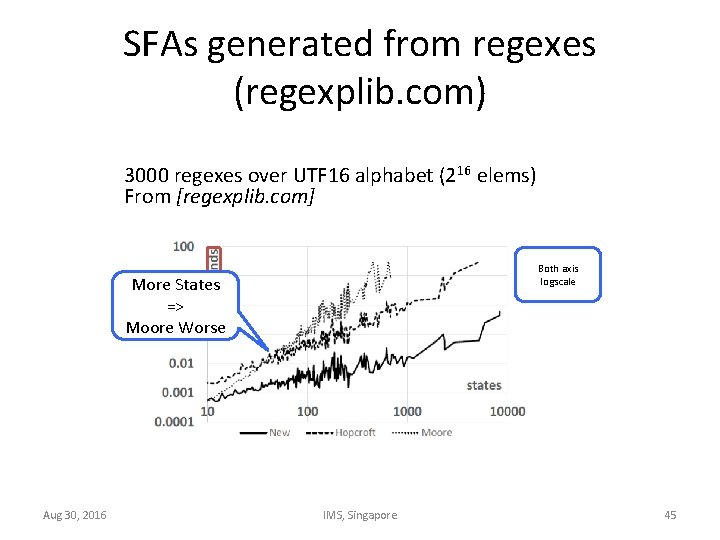
SFAs generated from regexes (regexplib. com) 3000 regexes over UTF 16 alphabet (216 elems) From [regexplib. com] Both axis logscale More States => Moore Worse Aug 30, 2016 IMS, Singapore 45
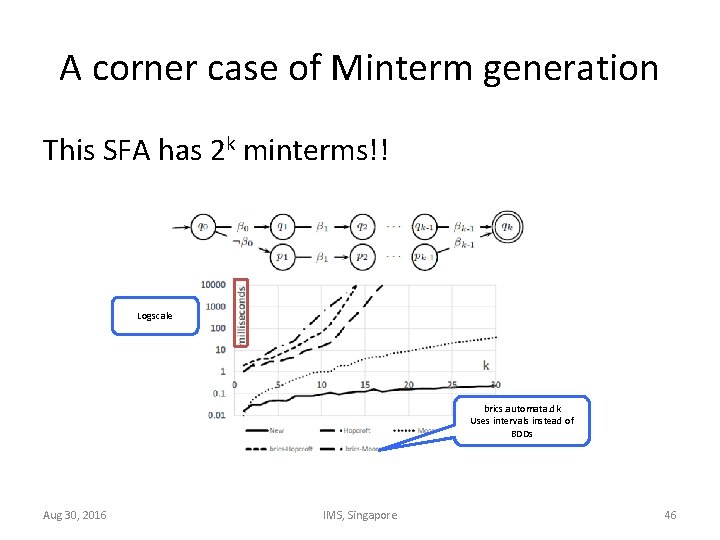
A corner case of Minterm generation This SFA has 2 k minterms!! Logscale brics. automata. dk Uses intervals instead of BDDs Aug 30, 2016 IMS, Singapore 46
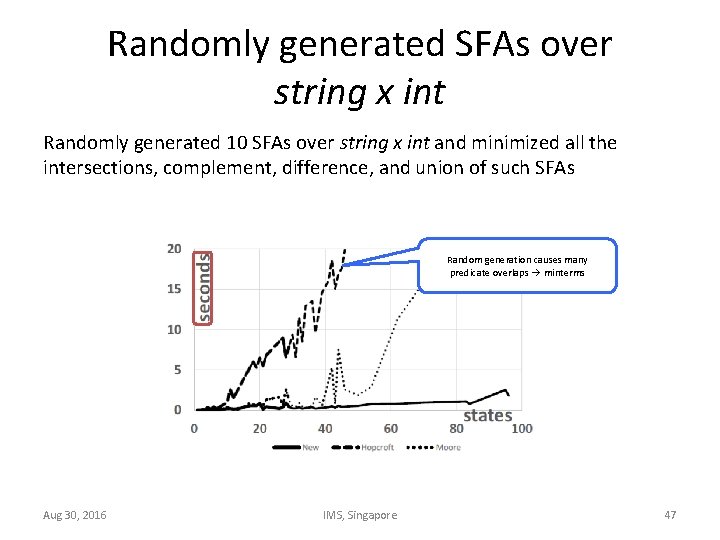
Randomly generated SFAs over string x int Randomly generated 10 SFAs over string x int and minimized all the intersections, complement, difference, and union of such SFAs Random generation causes many predicate overlaps minterms Aug 30, 2016 IMS, Singapore 47

Tutorial Overview Part 1 (s. FAs) Part 2 (Extensions) – symbolic finite automaton or s. FA • properties • key algorithms • Symbolic finite transducer – lookahead • lookahead elimination via Monadic Decomposition – s. M 2 L-str • key difference to M 2 L-str • translation to s. FAs • Cartesian Product of Effective Boolean Algebras Aug 30, 2016 – output IMS, Singapore – tree automata • Minimization – code generation • sequential code gen • parallel code gen 48
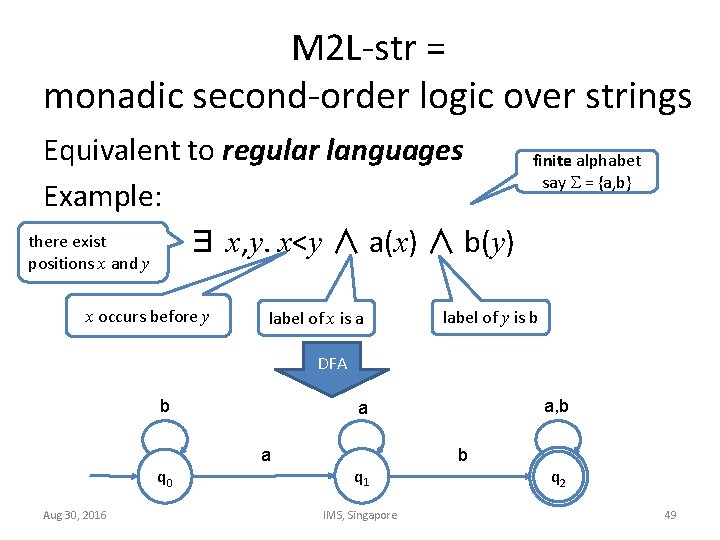
M 2 L-str = monadic second-order logic over strings Equivalent to regular languages Example: there exist ∃ x, y. x<y ∧ a(x) ∧ b(y) finite alphabet say = {a, b} positions x and y x occurs before y label of x is a label of y is b DFA b a q 0 Aug 30, 2016 a, b a q 1 IMS, Singapore b q 2 49
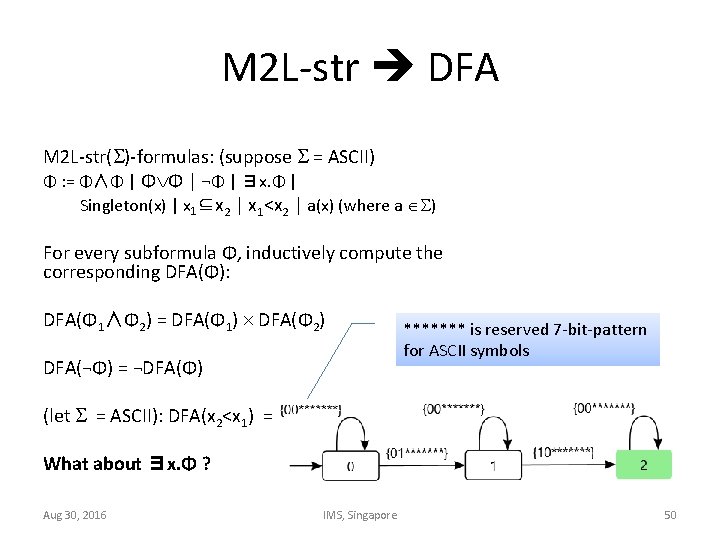
M 2 L-str DFA M 2 L-str( )-formulas: (suppose = ASCII) Φ : = Φ∧Φ | Φ Φ | ¬Φ | ∃x. Φ | Singleton(x) | x 1⊆x 2 | x 1<x 2 | a(x) (where a ) For every subformula Φ, inductively compute the corresponding DFA(Φ): DFA(Φ 1∧Φ 2) = DFA(Φ 1) DFA(Φ 2) DFA(¬Φ) = ¬DFA(Φ) ******* is reserved 7 -bit-pattern for ASCII symbols (let = ASCII): DFA(x 2<x 1) = What about ∃x. Φ ? Aug 30, 2016 IMS, Singapore 50
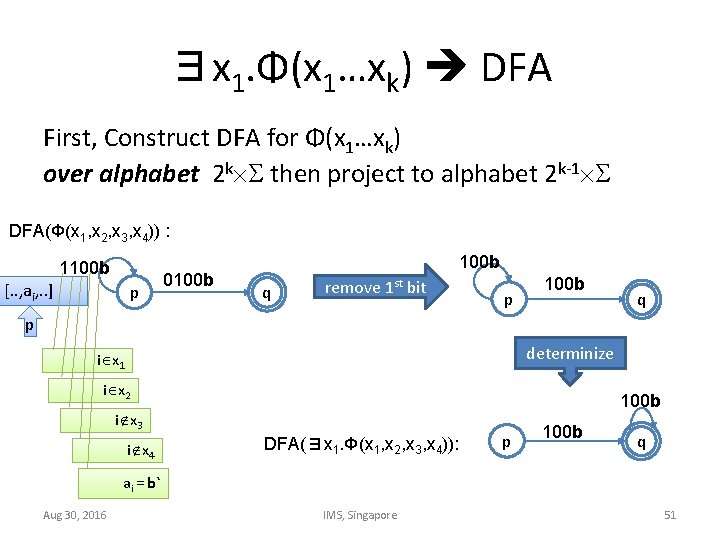
∃x 1. Φ(x 1…xk) DFA First, Construct DFA for Φ(x 1…xk) over alphabet 2 k then project to alphabet 2 k-1 DFA(Φ(x 1, x 2, x 3, x 4)) : 1100 b [. . , ai, . . ] p 0100 b q remove 1 st bit p 100 b q p determinize i x 1 i x 2 100 b i x 3 i x 4 DFA(∃x 1. Φ(x 1, x 2, x 3, x 4)): p 100 b q ai = b` Aug 30, 2016 IMS, Singapore 51
![s. M 2 L-str s. FA [(*1*0, _), (*0*1, _)] L(SFA(x 2<x 4)) s. s. M 2 L-str s. FA [(*1*0, _), (*0*1, _)] L(SFA(x 2<x 4)) s.](http://slidetodoc.com/presentation_image_h2/e5db78090456188bdc8ab90577dda1a5/image-52.jpg)
s. M 2 L-str s. FA [(*1*0, _), (*0*1, _)] L(SFA(x 2<x 4)) s. FA(xi < xj) s. FA(P (xi)) s. FA(Xj(xi)) a⊧ [(*0, _), (*1, a)] L(SFA(P (x 2)) s. FA( ) s. FA( ) ( s. FA( )C xi fo. FV( ) ) s. FA( xi ) s. FA( )↾i Aug 30, 2016 IMS, Singapore 52
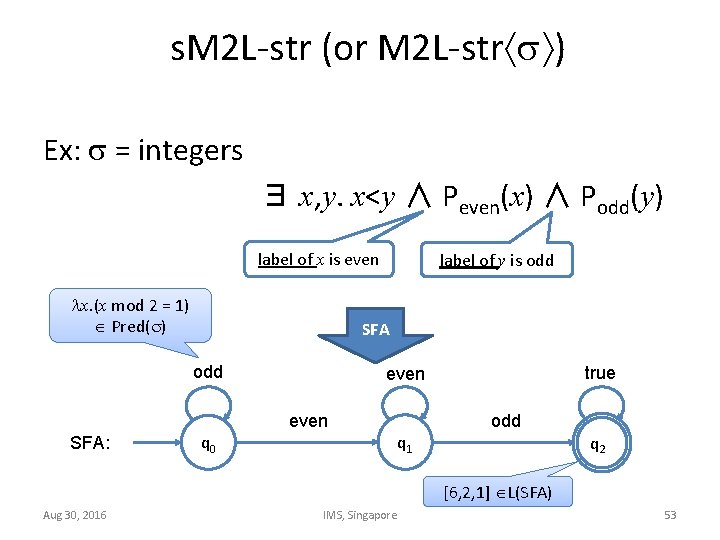
s. M 2 L-str (or M 2 L-str ) Ex: = integers ∃ x, y. x<y ∧ Peven(x) ∧ Podd(y) label of x is even x. (x mod 2 = 1) Pred( ) label of y is odd SFA odd even SFA: true even q 1 q 0 odd q 2 [6, 2, 1] L(SFA) Aug 30, 2016 IMS, Singapore 53

What is different about M 2 L-str compared to M 2 L-str? • The alphabet is given by an Effective Boolean Algebra A – the set of characters (elements of type ) may be infinite – is a set of predicates over elements of type , closed under Boolean operations • Formulas are constructed as before except for atoms P (x) where and x is f. o. – semantics: let w = [a 1, . . . , ak] and i {1. . . k} w ⊧ P (i) iff ai ⊧ Aug 30, 2016 IMS, Singapore 54

Example = ∀x((Odd(x) ⇒ Peven(x)) ∧ (Even(x) ⇒ Podd(x))) [a 1, . . . , ak] ⊧ iff for i [1. . k]: odd(ai) even(i) Aug 30, 2016 IMS, Singapore 55

New kinds of optimizations • P (x) is equivalent to P (x) where , the formula may be unsatisfiable • P (x) is equivalent to P (x) Aug 30, 2016 IMS, Singapore 56

Can we convert M 2 L-str ? Yes! But, in the worst case, at an exponential cost. minterms are nonempty regions in Given in Pred( -w. S 1 S): 1. take = { | P (x) occurs in } 2. let = {Pm | m minterms( )} 3. replace P (x) in by Pm 1(x) . . . Pmk(x) where {m 1. . . mk} = minterms that intersect e. g 4 1 2 4 3 Aug 30, 2016 IMS, Singapore 5 57

s. M 2 L-str s. FA What is the alphabet of the SFA of Φ(X 1. . . Xk)? Cartesian Product Algebra for A 2 k Key Challenges: 1. How to implement Boolean algebra for A B given implementations of Boolean algebras for A and B in particular when B = 2 k? 2. How to project A 2 k to A 2 k-1 ? Concrete scenario: suppose B = BDD solver, A = SMT solver Aug 30, 2016 IMS, Singapore 58

Representation 1 for A B • If-Then-Else dags – Shannon expansion whose • Nonterminal nodes are predicates of A • Terminal nodes are (inequivalent) predicates of B (BDDs) 1 2 1 2 represents the predicate in A B: (x, y). (( 1(x) 2(x)) 1(y)) (( 1(x) 2(x)) 2(y)) ( 1(x) 2(y)) Aug 30, 2016 IMS, Singapore 59

Representation 2 for A B • Algebraic Decision Diagrams, given B = 2 k, with depth k – Shannon expansion whose • Nonterminal nodes are individual bits (1. . k) • Terminal nodes are inequivalent predicates of A 1 2 1 2 construct the leaves with a predicate-trie represents the predicate in A B: (x, y). (( 1(y) 2(y)) 1(x)) (( 1(y) 2(y)) 2(x)) ( 1(y) 2(x)) Aug 30, 2016 IMS, Singapore 60
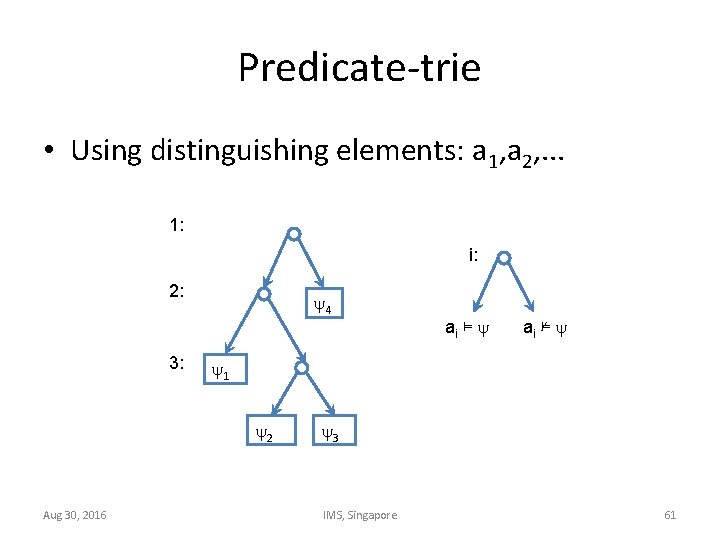
Predicate-trie • Using distinguishing elements: a 1, a 2, . . . 1: i: 2: 3: 4 ai ⊭ 1 2 Aug 30, 2016 ai ⊨ 3 IMS, Singapore 61
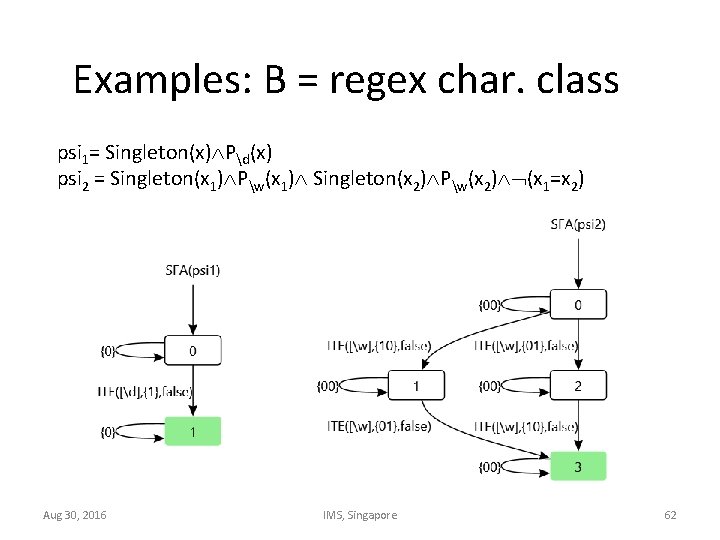
Examples: B = regex char. class psi 1= Singleton(x) Pd(x) psi 2 = Singleton(x 1) Pw(x 1) Singleton(x 2) Pw(x 2) (x 1=x 2) Aug 30, 2016 IMS, Singapore 62

Example: password generation • = regex char. classes over ASCII: (in M 2 L-str (+ syntactic sugar)) Passw. Pred = X. (|X|=12 Pw(X) P[^oei. OEI 4 -9](X)) y. (Pd(y) z. (y = z+1 PD(z))) For example: “c. Onn. Ect 2 w. If. I” L(SFA(Passw. Pred)) “c 0 nn 3 ct 2 w 1 f 1” L(SFA(Passw. Pred)) Aug 30, 2016 IMS, Singapore 63

Further thoughts on translating M 2 L-str to SFA Presented translation from M 2 L-str to SFA does not require determinization Alternatively one may consider: Nondeterministic SFAs Alternating SFAs – complementation? – minimization? Aug 30, 2016 – minimization? – projection? IMS, Singapore 64

Other possible symbolic extensions of MSO logics: • • • WS 1 S WS 2 S M 2 L-tree S 1 S S 2 S Aug 30, 2016 IMS, Singapore 65

PART 1 CONCLUSION Aug 30, 2016 IMS, Singapore 66

Symbolic automata • A versatile and powerful model for strings (and trees) over complex domains • Completely subsume classical automata • Separation of concerns between automata structure and alphabet • Opportunity for new algorithms that exploit SAT and SMT solvers Aug 30, 2016 IMS, Singapore 67

PART 2 (EXTENSIONS) Aug 30, 2016 IMS, Singapore 68

Tutorial Overview Part 1 (s. FAs) Part 2 (Extensions) – symbolic finite automaton or s. FA • properties • key algorithms • Symbolic finite transducer – lookahead • lookahead elimination via Monadic Decomposition – s. M 2 L-str • key difference to M 2 L-str • translation to s. FAs • Cartesian Product of Effective Boolean Algebras Aug 30, 2016 – output IMS, Singapore – tree automata • Minimization – code generation • sequential code gen • parallel code gen 69
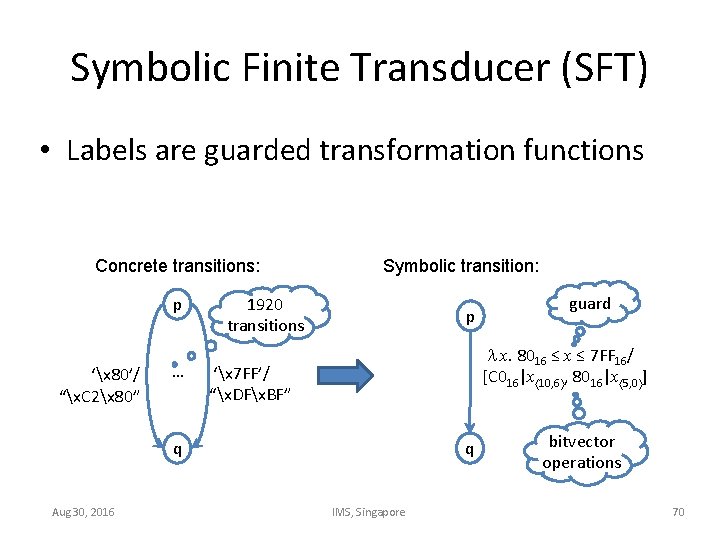
Symbolic Finite Transducer (SFT) • Labels are guarded transformation functions Concrete transitions: p ‘x 80’/ “x. C 2x 80” … Symbolic transition: 1920 transitions p x. 8016 ≤ x ≤ 7 FF 16/ [C 016|x 10, 6 , 8016|x 5, 0 ] ‘x 7 FF’/ “x. DFx. BF” q Aug 30, 2016 guard q IMS, Singapore bitvector operations 70
![SFT Execution Example x mod 2 =1/[x-1] x mod 2 =0/[x, x] x mod SFT Execution Example x mod 2 =1/[x-1] x mod 2 =0/[x, x] x mod](http://slidetodoc.com/presentation_image_h2/e5db78090456188bdc8ab90577dda1a5/image-71.jpg)
SFT Execution Example x mod 2 =1/[x-1] x mod 2 =0/[x, x] x mod 2 =0/[] p q x mod 2 =1/[x-1] Input tape 1 p Output tape Aug 30, 2016 2 p 0 5 q 2 3 p 2 IMS, Singapore p 4 2 71

Applications of SFTs • Security analysis of sanitizers – USENIX SECURITY’ 11 (Hooimeijer, Livshits, Molnar, Saxena, Veanes) • Analysis of string encoders/decoders – CAV’ 13 (D’Antoni, Veanes) Aug 30, 2016 IMS, Singapore 72

A string sanitizer • A string transformation function. Untrusted data Sanitized data “im. png' …” Aug 30, 2016 “img. png&#x 35; …” IMS, Singapore 73
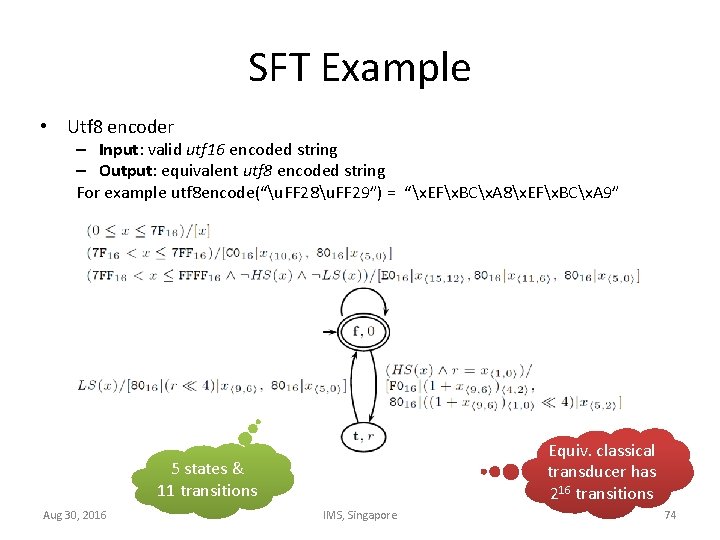
SFT Example • Utf 8 encoder – Input: valid utf 16 encoded string – Output: equivalent utf 8 encoded string For example utf 8 encode(“u. FF 28u. FF 29”) = “x. EFx. BCx. A 8x. EFx. BCx. A 9” Equiv. classical transducer has 216 transitions 5 states & 11 transitions Aug 30, 2016 IMS, Singapore 74
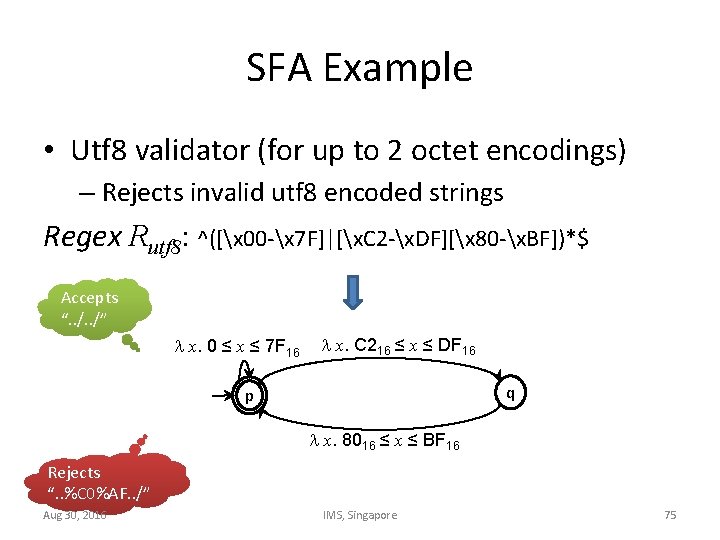
SFA Example • Utf 8 validator (for up to 2 octet encodings) – Rejects invalid utf 8 encoded strings Regex Rutf 8: ^([x 00 -x 7 F]|[x. C 2 -x. DF][x 80 -x. BF])*$ Accepts “. . /” x. 0 ≤ x ≤ 7 F 16 x. C 216 ≤ x ≤ DF 16 q p x. 8016 ≤ x ≤ BF 16 Rejects “. . %C 0%AF. . /” Aug 30, 2016 IMS, Singapore 75
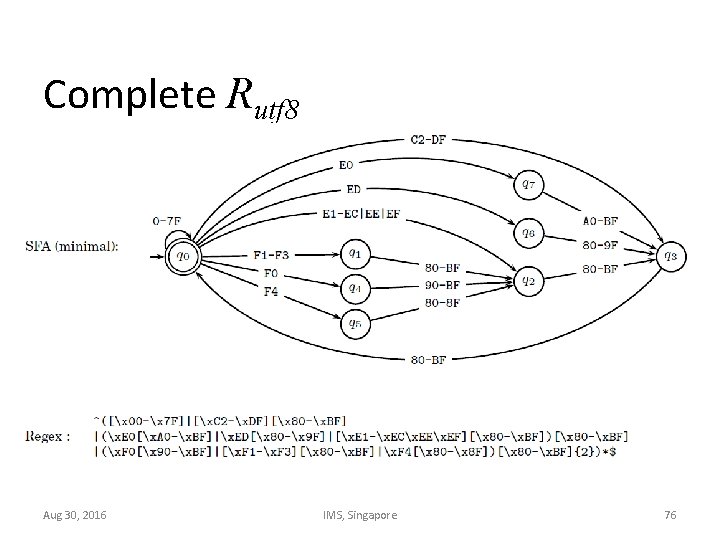
Complete Rutf 8 Aug 30, 2016 IMS, Singapore 76

SFT Application Analysis scenario • Valid inputs A = SFA(Rutf 8) • Invalid inputs (attack vectors) Ac = Complement(A) • Inputs accepted by Utf 8 Decode D = Domain(Utf 8 Decode) • Does Utf 8 Decode accept an invalid input? Ac D ? (e. g. "%c 0%ae" D) Aug 30, 2016 IMS, Singapore 77

We also want to analyze outputs • Want to analyze questions such as: Does Utf 8 Encode produce a bad output? x(Utf 8 Encode(x) Complement(SFA(Rutf 8))) ? Aug 30, 2016 IMS, Singapore 78

Bek (a frontend language for SFTs) program smileycipher(w) { return iter(c in w) { case(true): yield(0 x. D 83 D, (c - 'a') + 0 x. DE 00); }; } http: //www. rise 4 fun. com/Bek/ZH 0 Aug 30, 2016 IMS, Singapore 79

Why SFTs and SFAs? • They have good algebraic properties (POPL'12) – SFTs are closed under composition – Equivalence is decidable in the single-valued case – domain of an SFT is an SFA – SFAs are closed under Boolean operations • Useful for various analysis tasks Aug 30, 2016 IMS, Singapore 80
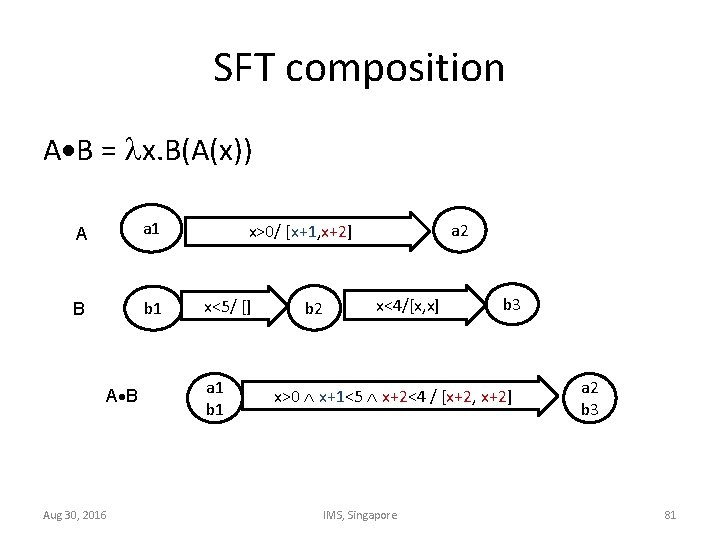
SFT composition A B = x. B(A(x)) A a 1 B b 1 A B Aug 30, 2016 a 2 x>0/ [x+1, x+2] x<5/ [] a 1 b 2 x<4/[x, x] b 3 x>0 x+1<5 x+2<4 / [x+2, x+2] IMS, Singapore a 2 b 3 81
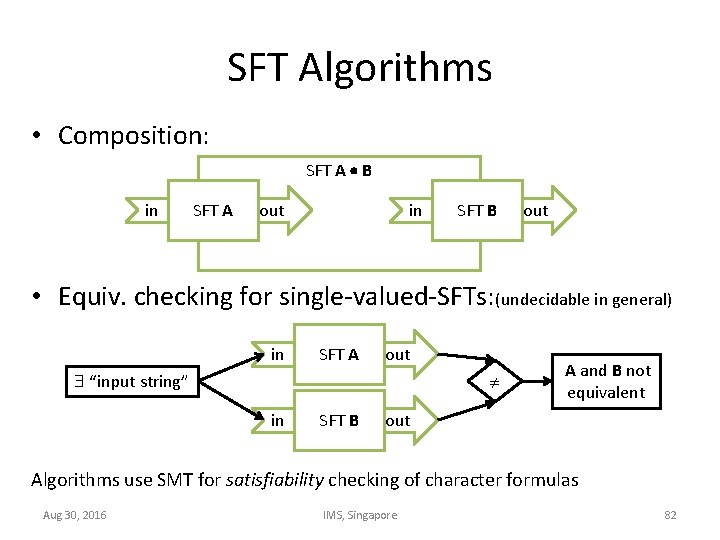
SFT Algorithms • Composition: SFT A B in SFT A out in SFT B out • Equiv. checking for single-valued-SFTs: (undecidable in general) in SFT A out “input string” in SFT B A and B not equivalent out Algorithms use SMT for satisfiability checking of character formulas Aug 30, 2016 IMS, Singapore 82
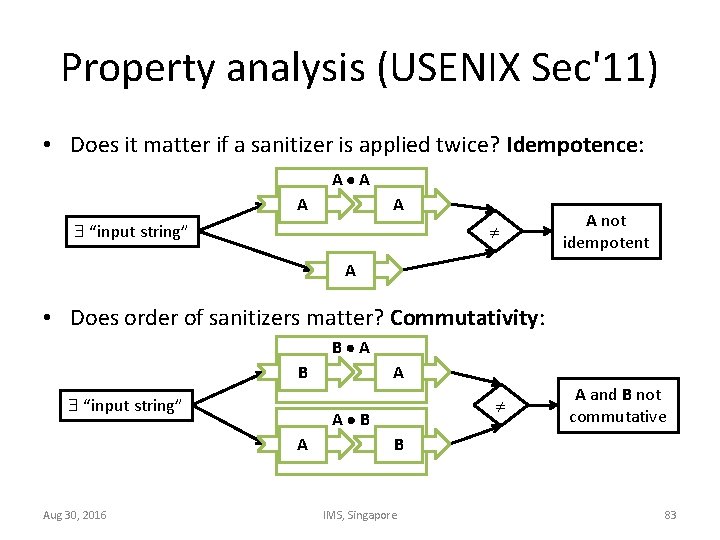
Property analysis (USENIX Sec'11) • Does it matter if a sanitizer is applied twice? Idempotence: A A “input string” A not idempotent A • Does order of sanitizers matter? Commutativity: B A B “input string” A B A Aug 30, 2016 A A and B not commutative B IMS, Singapore 83

Safety analysis Using solver • Algorithms for SFAs and SFTs. » extensions of classical algorithms modulo Th( ) • Example: suppose good output = "catfree" Catfree = [^u. DE 38 -u. DE 40]* bad output: Contains. ACat = Complement(Catfree) • x(smileycipher(x) Contains. ACat) ? {x | smileycipher(x) Contains. ACat} http: //www. rise 4 fun. com/Bek/n. Dx Aug 30, 2016 IMS, Singapore Does there exist an input x that causes a "cat" in the output ? 84

Tutorial Overview Part 1 (s. FAs) Part 2 (Extensions) – symbolic finite automaton or s. FA • properties • key algorithms • Symbolic finite transducer – lookahead • lookahead elimination via Monadic Decomposition – s. M 2 L-str • key difference to M 2 L-str • translation to s. FAs • Cartesian Product of Effective Boolean Algebras Aug 30, 2016 – output IMS, Singapore – tree automata • Minimization – code generation • sequential code gen • parallel code gen 85

ESFAs and ESFTs • Unlike in the classical case look-ahead breaks many properties – e. g. equivalence of ESFAs is undecidable x 1≤FF ∧ x 2≤FF ∧ x 3≤FF / [x 1>>2, ((x 1&3)<<4)|(x 2>>4), ((x 2&0 x. F)<<2)|(x 3>>6), x 3&0 x 3 F] q above ESFT, reads 3 and writes 4 symbols (base 64 encoder) M a n TWF u http: //www. rise 4 fun. com/Bex/tutorial/guide Aug 30, 2016 IMS, Singapore 86
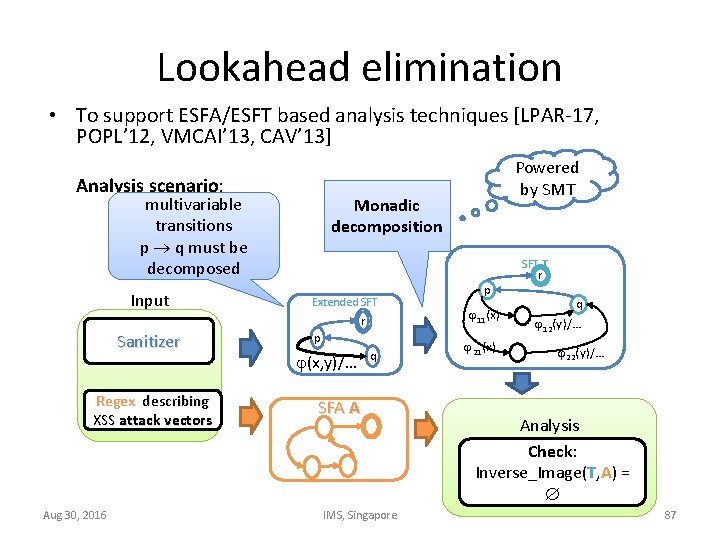
Lookahead elimination • To support ESFA/ESFT based analysis techniques [LPAR-17, POPL’ 12, VMCAI’ 13, CAV’ 13] Analysis scenario: multivariable transitions p q must be decomposed Input Monadic decomposition Extended SFT r Sanitizer Regex describing XSS attack vectors Aug 30, 2016 Powered by SMT p (x, y)/… q SFA A IMS, Singapore p 11(x) 21(x) SFT T r q 12(y)/… 22(y)/… Analysis Check: Inverse_Image(T, A) = 87

Example of a monadic formula Consider integer linear arithmetic (x, y) = x + (y mod 2) > 5 Monadic width = 2 ((x > 5) even(y)) ((x + 1 > 5) odd(y)) Cartesian Aug 30, 2016 Cartesian IMS, Singapore 88

Example of a nonmonadic formula Consider integer linear arithmetic (x, y) = x<y No finite decomposition exists (x < 0 0 y) (x < 1 1 y) … Aug 30, 2016 IMS, Singapore 89

What is monadic decomposition? Some terminology: Unary formula with (at most) one free variable MNF Monadic Normal Form Boolean combination of unary formulas (x, y) monadic decomposition MNF(x, y) is monadic if has an equivalent MNF Related to variable independence (Libkin 2003) Aug 30, 2016 IMS, Singapore 90

Formal definition of Monadic Decomposition { <, = , +, -, modk } Q. F. L. A. Z Fix: Signature , r. e. fragment F of -formulas, and r. e. -structure M Assumptions about. F : • Closed under Boolean operations: , ∈ F , , ∈ F • Closed under value substitutions: ∈ F, a ∈ M [x/a] ∈ F • Decidable: M ⊧ ∃x (x) is decidable for (x) ∈ F Main two questions: 1) Decide if is monadic, i. e. , does have a MNF in M? 2) Assume is monadic, construct a MNF of using a solver for F x + (y mod 2) > 5 Aug 30, 2016 (x > 5 y mod 2 = 0) (x > 4 y mod 2 = 1) IMS, Singapore e. g. Z 3 91

Monadic Decomposition algorithm (intuition) Ex: (x, y) y>0 y&(y-1)=0 x&(y%7) 0 Intuition: 1. 2. 3. 4. Mark all (a, b) s. t. (a, b) holds Define b ~ c x( (x, b) (x, c)) 3 ~equiv classes: [1]~, [2]~, [4]~ Construct b(y) s. t. y( b(y) b ~ y) e. g. 1(y) n(y = 2 n n mod 3 = 0) Final decomposition is: 1(y) (x, 1) 2(y) (x, 2) 4(y) (x, 4) y 8 IMS, Singapore 7 6 5 4 4~ 32 2~ 16 1~ 8 x 3 2 1 1 Aug 30, 2016 2 3 4 5 6 7 8 9 92

Monadic decomposition algorithm (CAV’ 14) • Avoids DNF and full exploration of X~ and Y~ Theorem: If is monadic then mondec( ) is in MNF and equivalent to . Aug 30, 2016 IMS, Singapore 93

mondec impl. (z 3 py) Aug 30, 2016 IMS, Singapore 94
Some experiments Aug 30, 2016 IMS, Singapore 95

Remarks about monadic decomposition When can we decide if is monadic? • General case: undecidable – follows from undecidability of variable-independence (Libkin 03). • Decidable cases: – Integer Linear arithmetic. – Algebraic real arithmetic with addition and multiplication – EUF Potential applications (other than Symbolic Automata/Transducers): • theorem proving • program analysis • program synthesis • optimization problems • database applications Aug 30, 2016 IMS, Singapore 96

Tutorial Overview Part 1 (s. FAs) Part 2 (Extensions) – symbolic finite automaton or s. FA • properties • key algorithms • Symbolic finite transducer – lookahead • lookahead elimination via Monadic Decomposition – s. M 2 L-str • key difference to M 2 L-str • translation to s. FAs • Cartesian Product of Effective Boolean Algebras Aug 30, 2016 – output IMS, Singapore – tree automata • Minimization – code generation • sequential code gen • parallel code gen 97

Why symbolic tree automata? • Trees are common input/output data structures – XML query, type-checking, etc… – Natural Language translators (from parse tree to parse tree) – Compilers/optimizers (from parse tree to parse tree) Compilers – Tree manipulating programs: data structures algorithms, ontologies etc… – Augmented Reality – http: //www. rise 4 fun. com/Fast/tutorial/guide Aug 30, 2016 IMS, Singapore 98
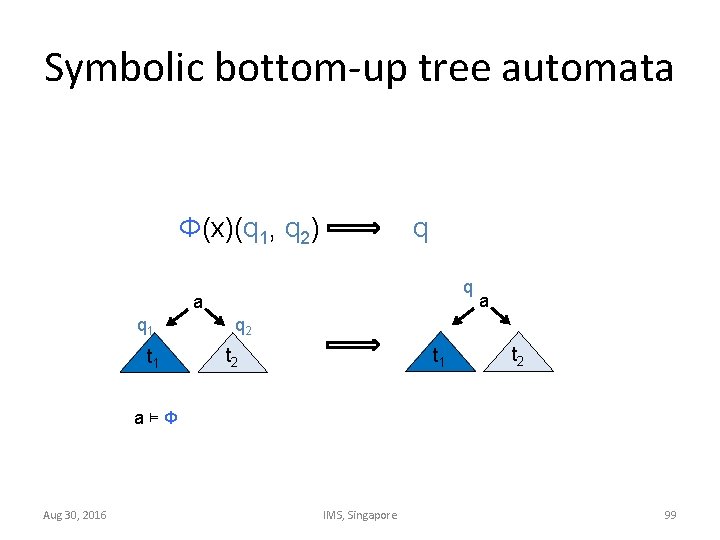
Symbolic bottom-up tree automata Φ(x)(q 1, q 2) q q a q 1 t 1 a q 2 t 1 t 2 a⊨Φ Aug 30, 2016 IMS, Singapore 99
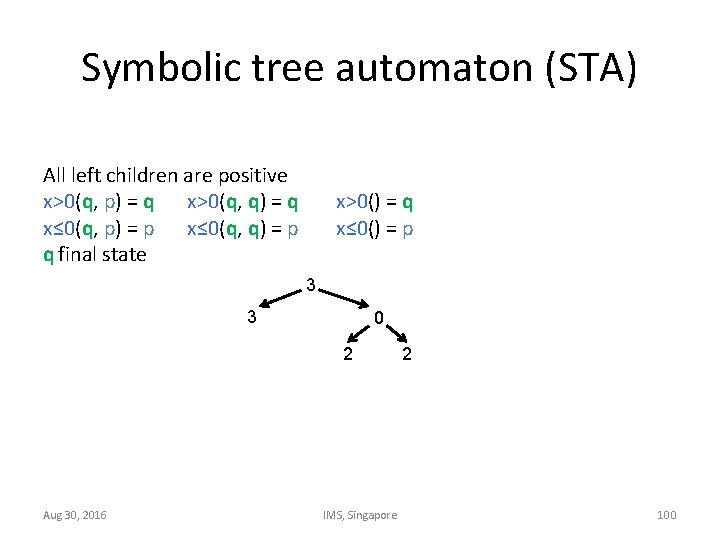
Symbolic tree automaton (STA) All left children are positive x>0(q, p) = q x>0(q, q) = q x≤ 0(q, p) = p x≤ 0(q, q) = p q final state x>0() = q x≤ 0() = p 3 3 0 2 Aug 30, 2016 IMS, Singapore 2 100
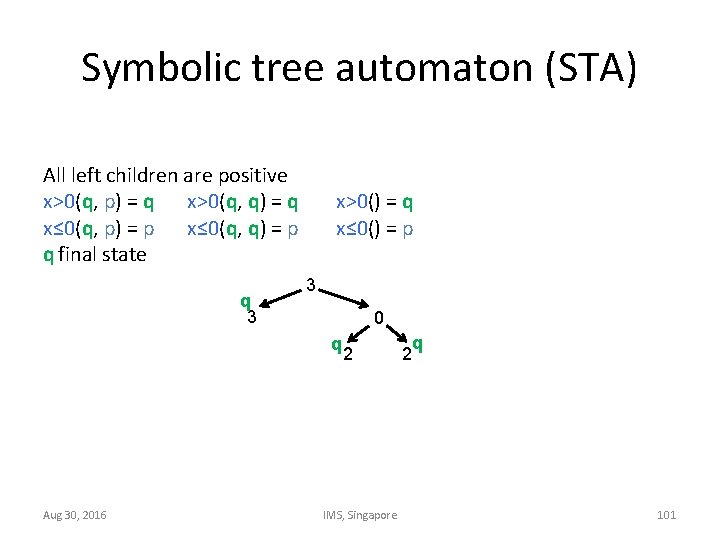
Symbolic tree automaton (STA) All left children are positive x>0(q, p) = q x>0(q, q) = q x≤ 0(q, p) = p x≤ 0(q, q) = p q final state q 3 x>0() = q x≤ 0() = p 3 0 q Aug 30, 2016 2 IMS, Singapore q 2 101
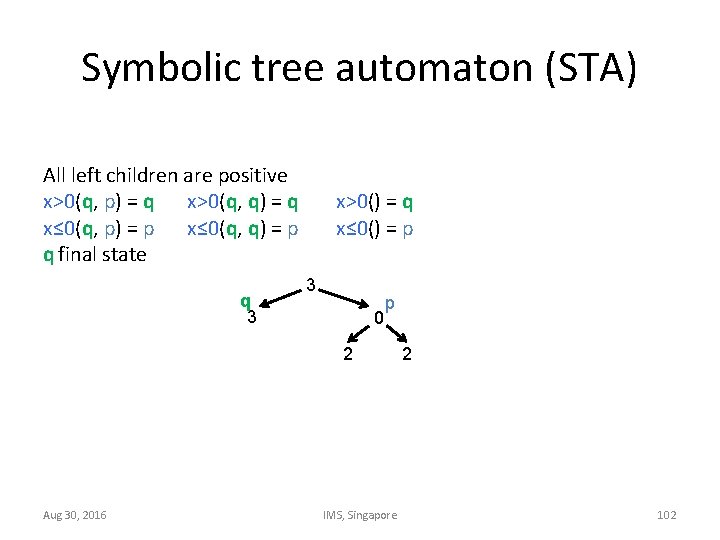
Symbolic tree automaton (STA) All left children are positive x>0(q, p) = q x>0(q, q) = q x≤ 0(q, p) = p x≤ 0(q, q) = p q final state q 3 x>0() = q x≤ 0() = p 3 0 p 2 Aug 30, 2016 IMS, Singapore 2 102
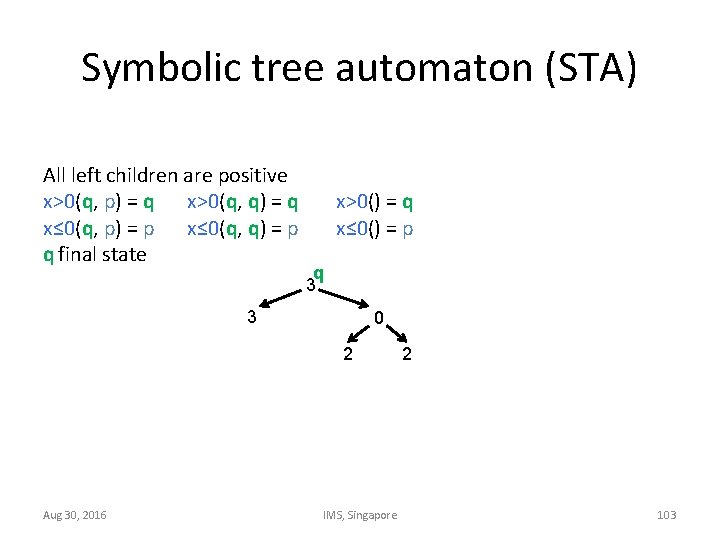
Symbolic tree automaton (STA) All left children are positive x>0(q, p) = q x>0(q, q) = q x≤ 0(q, p) = p x≤ 0(q, q) = p q final state x>0() = q x≤ 0() = p q 3 3 0 2 Aug 30, 2016 IMS, Singapore 2 103

HTML Sanitization • Removing malicious active code from HTML documents is a tree transformation body SANITIZE script div malicious code p p “Today I’m happy” Aug 30, 2016 IMS, Singapore div 104
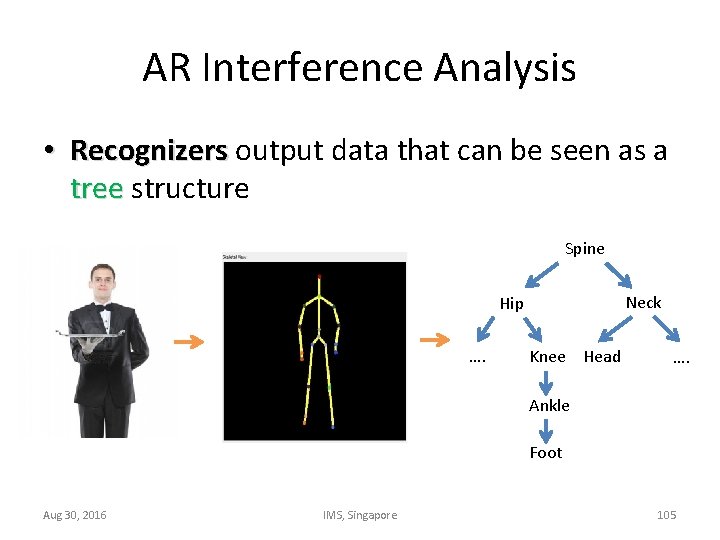
AR Interference Analysis • Recognizers output data that can be seen as a tree structure Spine Neck Hip …. Knee Head …. Ankle Foot Aug 30, 2016 IMS, Singapore 105
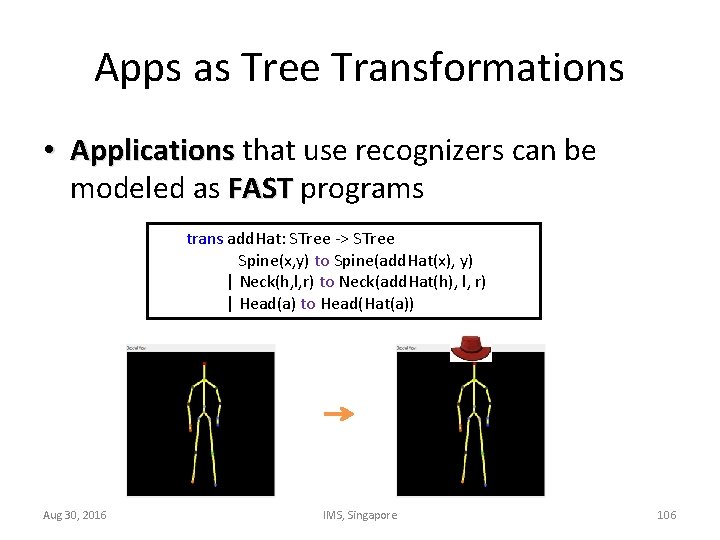
Apps as Tree Transformations • Applications that use recognizers can be modeled as FAST programs trans add. Hat: STree -> STree Spine(x, y) to Spine(add. Hat(x), y) | Neck(h, l, r) to Neck(add. Hat(h), l, r) | Head(a) to Head(Hat(a)) Aug 30, 2016 IMS, Singapore 106
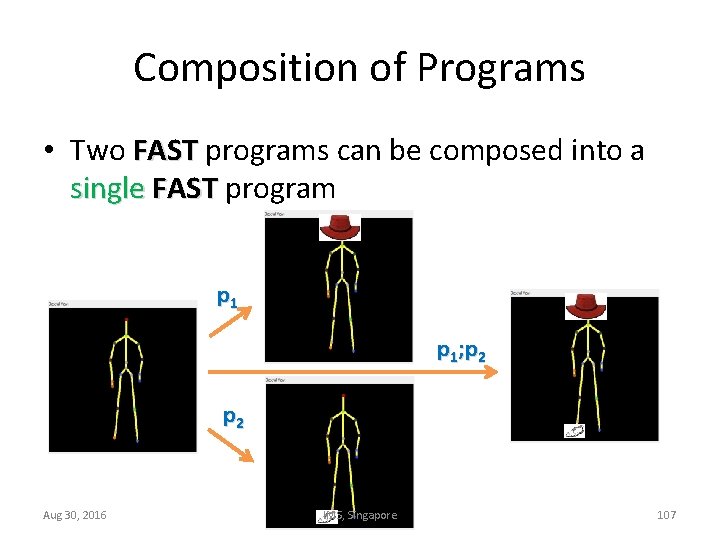
Composition of Programs • Two FAST programs can be composed into a single FAST program p 1; p 2 Aug 30, 2016 IMS, Singapore 107
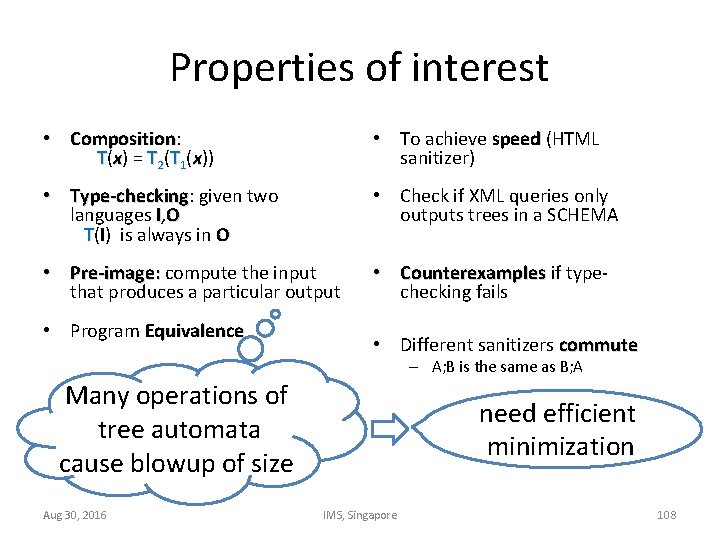
Properties of interest • Composition: Composition T(x) = T 2(T 1(x)) • To achieve speed (HTML sanitizer) • Type-checking: Type-checking given two languages I, O T(I) is always in O • Check if XML queries only outputs trees in a SCHEMA • Pre-image: compute the input that produces a particular output • Counterexamples if typechecking fails • Program Equivalence • Different sanitizers commute – A; B is the same as B; A Many operations of tree automata cause blowup of size Aug 30, 2016 need efficient minimization IMS, Singapore 108
![Good theories can be reused [LICS 16] MINIMIZATION OF SYMBOLIC TREE AUTOMATA Aug 30, Good theories can be reused [LICS 16] MINIMIZATION OF SYMBOLIC TREE AUTOMATA Aug 30,](http://slidetodoc.com/presentation_image_h2/e5db78090456188bdc8ab90577dda1a5/image-109.jpg)
Good theories can be reused [LICS 16] MINIMIZATION OF SYMBOLIC TREE AUTOMATA Aug 30, 2016 IMS, Singapore 109
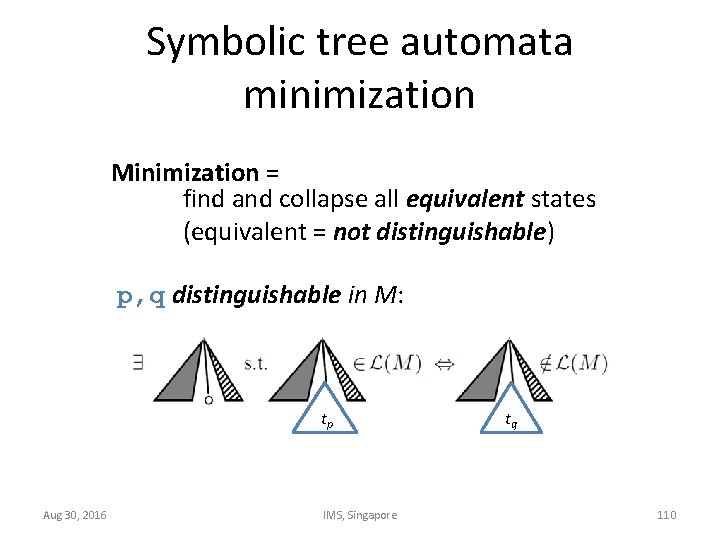
Symbolic tree automata minimization Minimization = find and collapse all equivalent states (equivalent = not distinguishable) p, q distinguishable in M: tp Aug 30, 2016 IMS, Singapore tq 110

How to minimize STAs 1. Symbolic generalization of Moore ‘s algorithm for STAs 2. Reduction of Symbolic Tree Automata minimization to Symbolic Finite Automata minimization Aug 30, 2016 IMS, Singapore 111
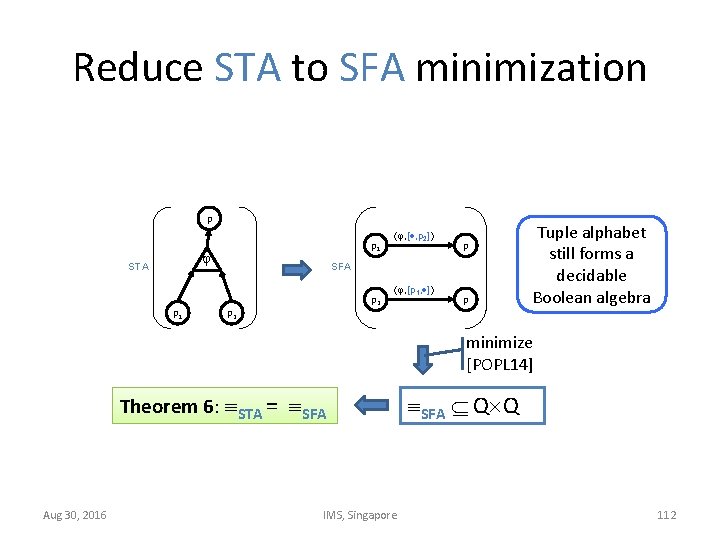
Reduce STA to SFA minimization p p 1 STA p 1 , [ , p 2] p SFA p 2 , [p 1, ] p Tuple alphabet still forms a decidable Boolean algebra minimize [POPL 14] Theorem 6: STA = SFA Aug 30, 2016 IMS, Singapore SFA Q Q 112
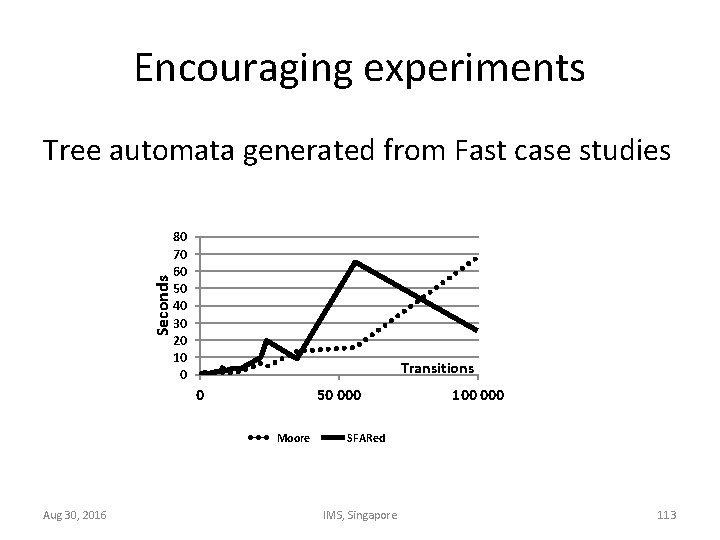
Encouraging experiments Seconds Tree automata generated from Fast case studies 80 70 60 50 40 30 20 10 0 Transitions 0 50 000 Moore Aug 30, 2016 100 000 SFARed IMS, Singapore 113

Tutorial Overview Part 1 (s. FAs) Part 2 (Extensions) – symbolic finite automaton or s. FA • properties • key algorithms • Symbolic finite transducer – lookahead • lookahead elimination via Monadic Decomposition – s. M 2 L-str • key difference to M 2 L-str • translation to s. FAs • Cartesian Product of Effective Boolean Algebras Aug 30, 2016 – output IMS, Singapore – tree automata • Minimization – code generation • sequential code gen • parallel code gen 114
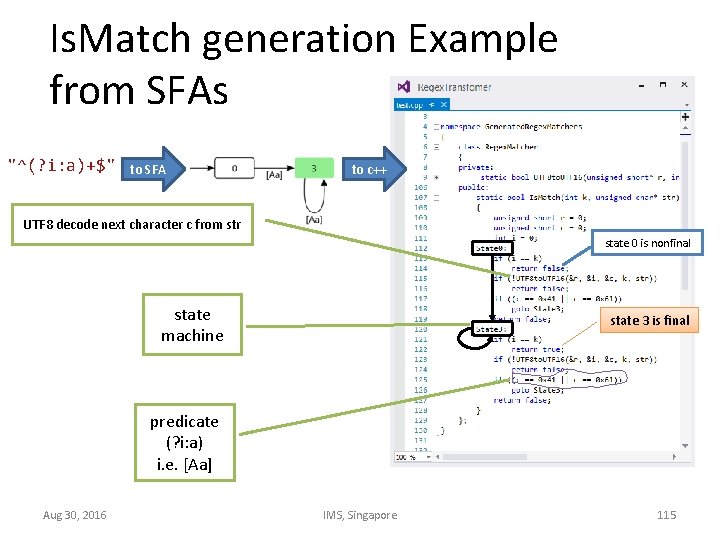
Is. Match generation Example from SFAs "^(? i: a)+$" to SFA to c++ UTF 8 decode next character c from str state 0 is nonfinal state machine state 3 is final predicate (? i: a) i. e. [Aa] Aug 30, 2016 IMS, Singapore 115

One reason to specialize Is. Match: is to avoid DOS attacks 60000 “Evil” regexes: regex: @"^(([a-z])+. )+[A-Z]([a-z])+$" input: "aaa aaa". . . Is. Match time in ms 1) 50000 40000 30000 20000 10000 0 12 13 14 15 16 17 input length 60000 50000 regex: "^(_? a? _? )+$" input: "_a_aa_aa_ _aa@". . . Aug 30, 2016 Is. Match time in ms 2) 40000 30000 20000 10000 0 121314151617 IMS, Singapore input length 116
![parallelization [POPL’ 15] BEK MONADIC ESFTS PARALLEL CODE Aug 30, 2016 IMS, Singapore 117 parallelization [POPL’ 15] BEK MONADIC ESFTS PARALLEL CODE Aug 30, 2016 IMS, Singapore 117](http://slidetodoc.com/presentation_image_h2/e5db78090456188bdc8ab90577dda1a5/image-117.jpg)
parallelization [POPL’ 15] BEK MONADIC ESFTS PARALLEL CODE Aug 30, 2016 IMS, Singapore 117
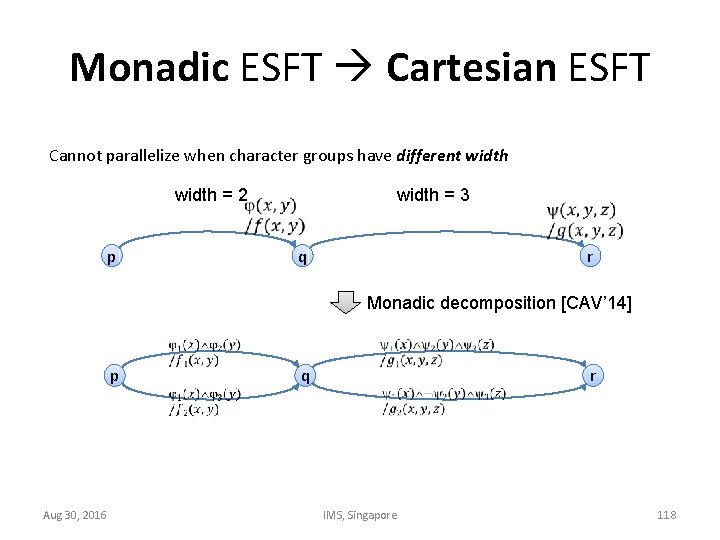
Monadic ESFT Cartesian ESFT Cannot parallelize when character groups have different width = 2 p width = 3 q r Monadic decomposition [CAV’ 14] p Aug 30, 2016 q r IMS, Singapore 118

CARTESIAN ESFT K-SFT Aug 30, 2016 IMS, Singapore 119
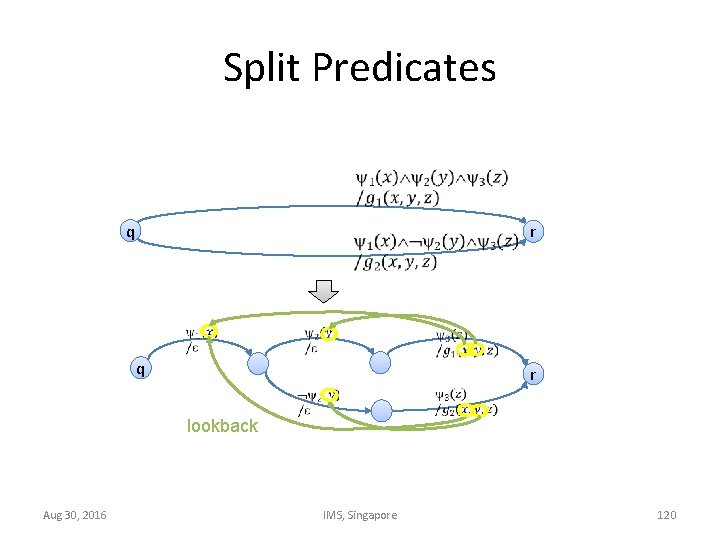
Split Predicates q r lookback Aug 30, 2016 IMS, Singapore 120
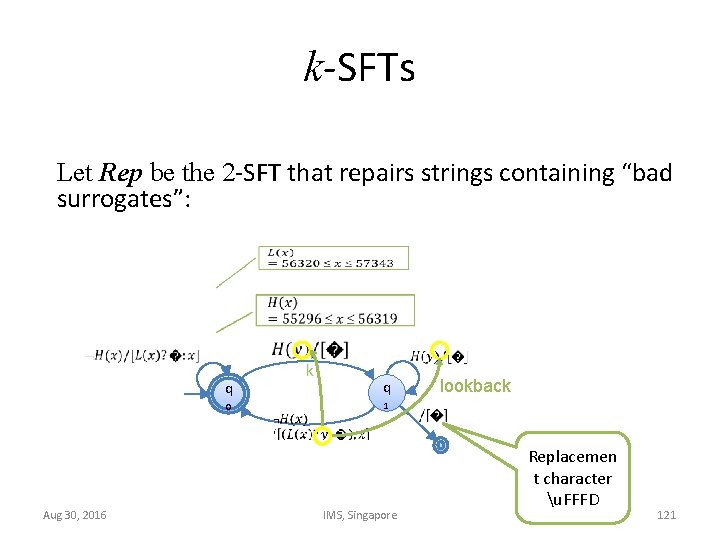
k-SFTs Let Rep be the 2 -SFT that repairs strings containing “bad surrogates”: Aug 30, 2016 q q 0 1 IMS, Singapore lookback Replacemen t character u. FFFD 121
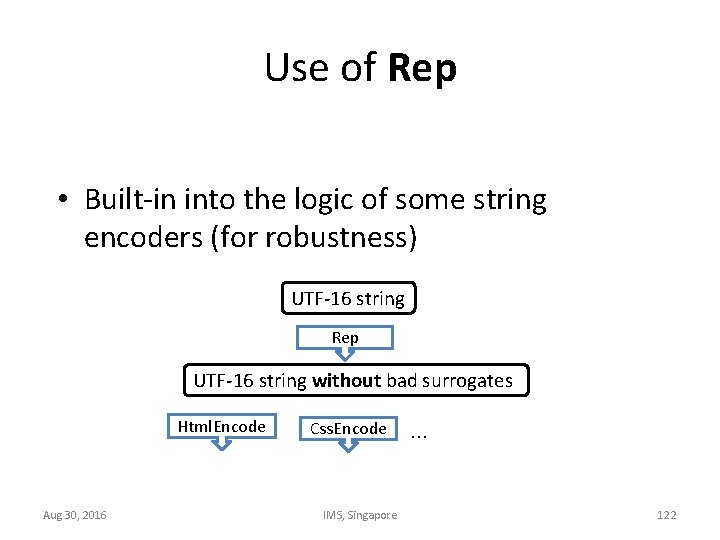
Use of Rep • Built-in into the logic of some string encoders (for robustness) UTF-16 string Rep UTF-16 string without bad surrogates Html. Encode Aug 30, 2016 Css. Encode IMS, Singapore … 122

K-SFTS ARE PARALLELIZABLE Aug 30, 2016 IMS, Singapore 123
Parallelization Step 1 • H(y)/ Aug 30, 2016 q q 0 1 q q 2 3 IMS, Singapore 124
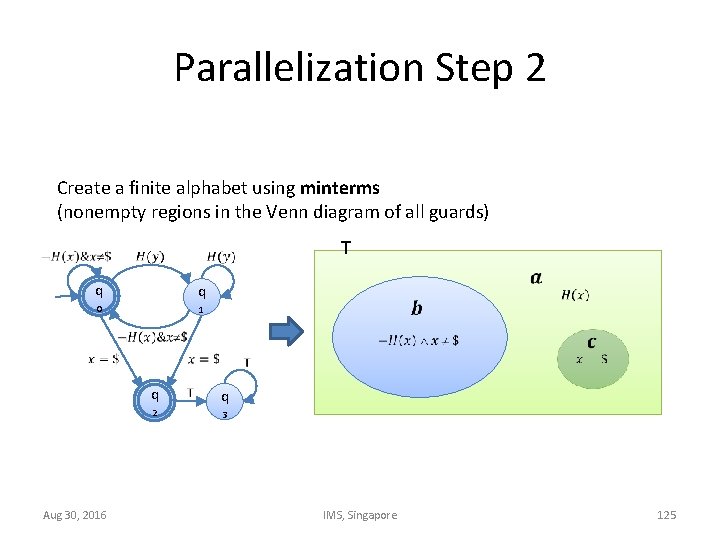
Parallelization Step 2 Create a finite alphabet using minterms (nonempty regions in the Venn diagram of all guards) T q q 0 1 Aug 30, 2016 q q 2 3 IMS, Singapore 125
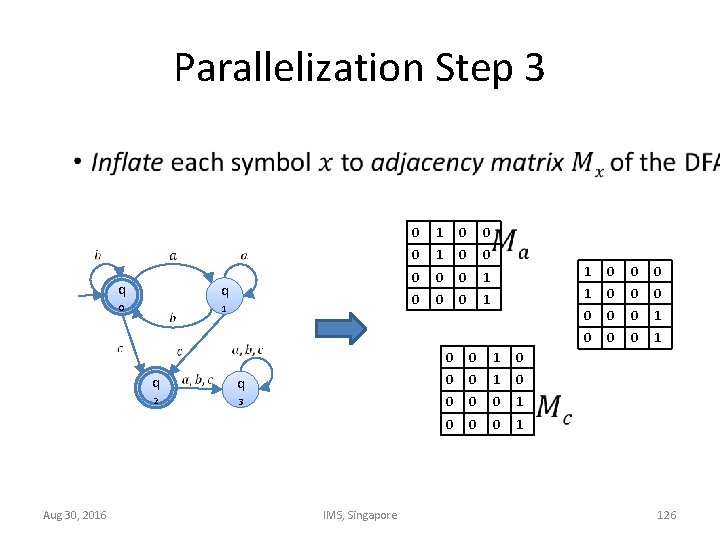
Parallelization Step 3 • Aug 30, 2016 q q 0 1 0 0 0 1 0 q q 0 0 1 0 2 3 0 0 0 1 IMS, Singapore 1 0 0 0 1 126
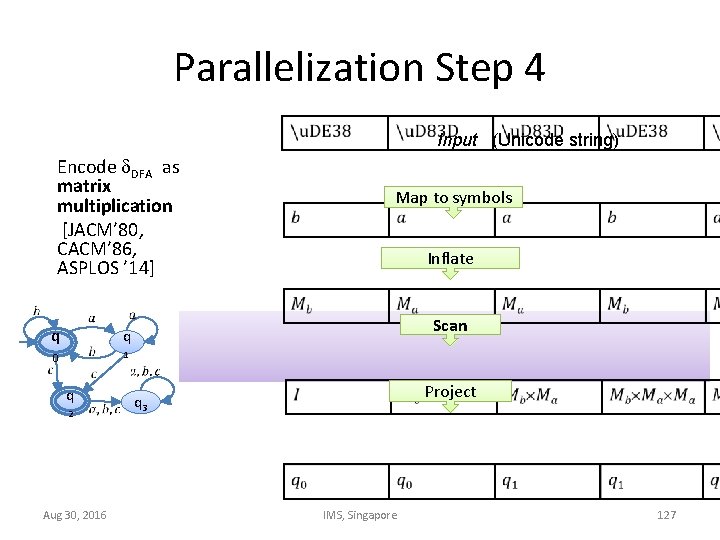
Parallelization Step 4 Input (Unicode string) Encode DFA as matrix multiplication [JACM’ 80, CACM’ 86, ASPLOS ’ 14] q q 0 1 q 2 Aug 30, 2016 Map to symbols Inflate Scan Project q 3 IMS, Singapore 127
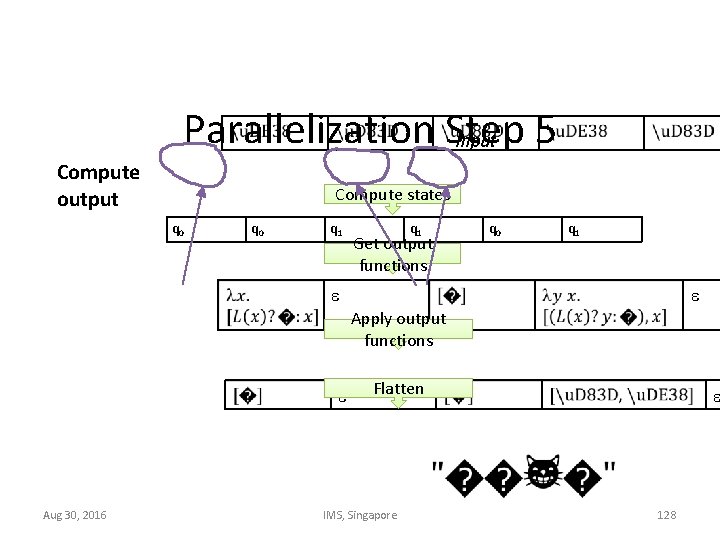
Parallelization Step 5 Input Compute output Compute states q 0 q 1 Get output functions q 0 q 1 Apply output functions Aug 30, 2016 Flatten IMS, Singapore 128

Tools using symbolic automata proving correctness of string encoders DRe. X efficient string manipulations theory of sequences automatic program inversion intelligent tutoring system for theory of computation SVPAlib open source analysis of tree manipulations Automata. Dot. Net open source. Net library http: //github. com/Automata. Dot. Net Java library Aug 30, 2016 genic IMS, Singapore 129
- Slides: 129